react hooks 的useState:
React 的 useState Hook 是一种用于在函数组件中管理状态的机制。它可以让函数组件具有类似于类组件的状态管理能力。
useState Hook 接收一个初始值作为参数,并返回一个包含状态值和更新状态值的数组。
import { useState } from 'react';const [state, setState] = useState(initialValue);
其中,state 表示当前的状态值,setState 是用于更新状态值的函数。
在函数组件中使用 useState 的示例:
import { useState } from 'react';function Counter() {const [count, setCount] = useState(0);const increment = () => {setCount(count + 1);};return (<div><p>Count: {count}</p><button onClick={increment}>Increment</button></div>);
}
在这个例子中,count 是状态值,初次渲染时被设置为 0。increment 函数用于更新 count 的值,通过调用 setCount 来触发状态的更新。
每当组件重新渲染时,useState 的初始值将被忽略,而是使用上一次渲染的状态值。这使得 useState 成为一种可实现记忆化状态的机制。
使用 useState Hook 可以在函数组件中方便地使用和管理状态,它为函数组件提供了一种简洁和灵活的状态管理方式。
相关文章:

react hooks 的useState:
React 的 useState Hook 是一种用于在函数组件中管理状态的机制。它可以让函数组件具有类似于类组件的状态管理能力。 useState Hook 接收一个初始值作为参数,并返回一个包含状态值和更新状态值的数组。 import { useState } from react;const [state, setState] …...
编程那么难,为什么不弄一个大众一学就会的计算机语言呢?
大家好!今天要和大家聊聊一个有趣的想法: 想象一下,如果编程变得像拼乐高积木一样简单,那将是多么美妙的事情啊!不需要费尽心思去学习繁杂的语法规则和复杂的逻辑,只需要将代码块像积木一样拼接起来&#x…...

论文阅读2---多线激光lidar内参标定原理
前言:该论文介绍多线激光lidar的标定内参的原理,有兴趣的,可研读原论文。 1、标定参数 rotCorrection:旋转修正角,每束激光的方位角偏移(与当前旋转角度的偏移,正值表示激光束逆时针旋转&…...

Ubuntu 22.04 apt 安装 ros1 ros Noetic Ninjemys
众所周知 ros2还有很多功能没有移植,而ros1官方不再支持 ubuntu 20.04 之后的版本。另一方面Ubuntu 22.04 更新了很多对新硬件的驱动,有更好的兼容性和体验,这就变的很纠结。 如果想在 22.04 使用最新版本的 ros noetic 只有自己编译一个办法…...

单片机学习笔记---矩阵键盘
目录 矩阵键盘的介绍 独立按键和矩阵按键的相同之处: 矩阵按键的扫描 代码演示 代码模块化移植 Keil自定义模板步骤: 代码编写 矩阵键盘就是开发板上右下角的这个模块 这一节的代码是基于上一节讲的LCD1602液晶显示屏驱动代码进行的 矩阵键盘的介…...

第八篇 交叉编译华为云Iot SDK到Orangepi3B
本篇主要内容: 一、交叉编译华为云Iot SDK依赖1.宿主机安装交叉编译工具链(1)选择下载交叉编译工具链(2)解压、添加环境变量、重启2.交叉编译依赖库(0) 准备工作(1) 交叉…...

软件工程测试2
1.【单选】“数据流的分解一般达到2层数据流就截止”的说法是否正确 A. 正确 B. 错误 答案:B 2.【单选】 在类图中,哪种关系表达总体与局部的关系 A. 泛化 B. 实现 C. 聚合 D. 依赖 答案:C 3.【多选】从UML时序图中我们能够得到(…...
)
31.【TypeScript 教程】混入(Mixins)
TypeScript 混入(Mixins) 混入(Mixins)是面向对象编程中的一个比较重要的概念。本节将会通过一个实例逐步介绍混入是如何在 TypeScript 中使用的。 1. 解释 在 TypeScript 中,可以根据不同的功能定义多个可复用的类,它们将作为 …...

C语言常见面试题:什么是联合体,联合体的作用是什么?
联合体(union)是一种特殊的数据类型,它可以在同一块内存单元中存储不同的数据类型。联合体的作用在于能够节省内存空间,并且可以用来实现数据的共享和交换。 联合体的定义方式是在C语言中通过关键字union来定义,例如&…...
Nginx进阶篇【五】
Nginx进阶篇【五】 八、Nginx实现服务器端集群搭建8.1.Nginx与Tomcat部署8.1.1.环境准备(Tomcat)8.1.1.1.浏览器访问:8.1.1.2.获取动态资源的链接地址:8.1.1.3.在Centos上准备一个Tomcat作为后台web服务器8.1.1.4.准备一个web项目,将其打包为war8.1.1.5.启动tomcat进…...

IndexedDB
Web SQL Database | Can I use... Support tables for HTML5, CSS3, etc IndexedDB | Can I use... Support tables for HTML5, CSS3, etc 为什么websql被废弃?_笔记大全_设计学院 WebSQL有兼容、性能、安全问题,要考虑使用IndexedDB替代。 一文看懂 In…...
git用法总结
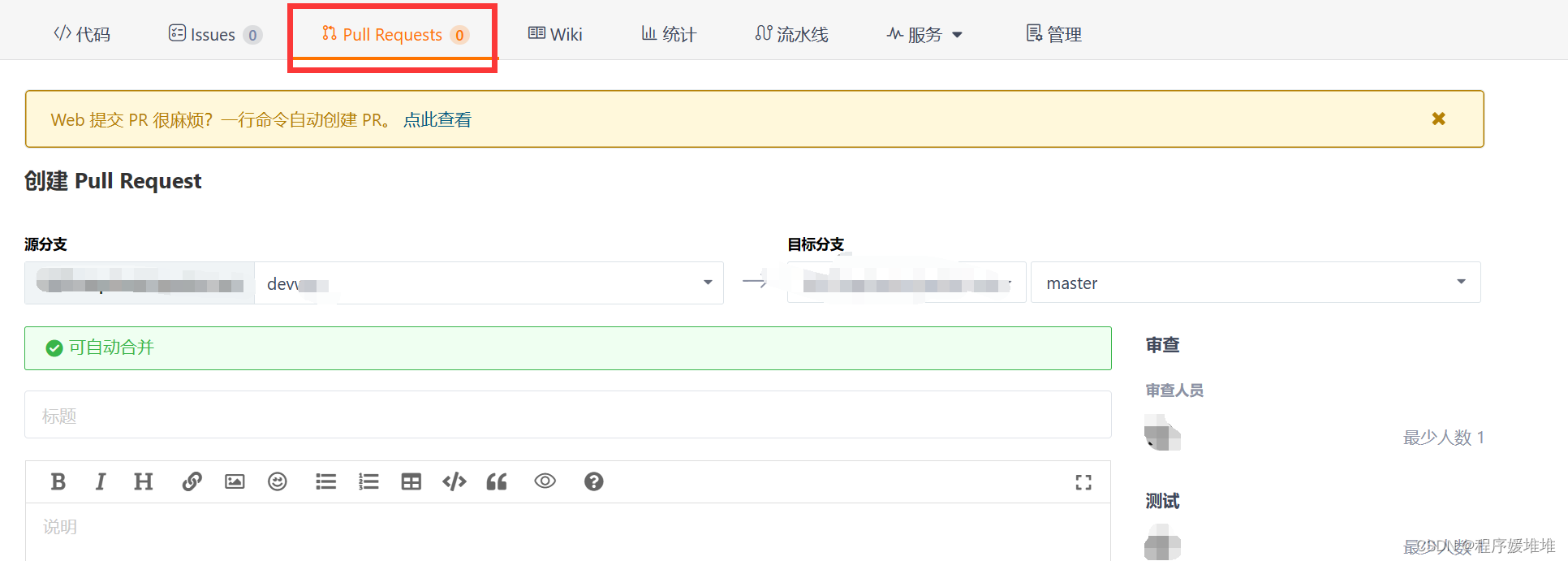
以gitee为例,GitHub也可参考本文 创建远程仓库 在自己的gitee主页 创建本地仓库 在文件夹下,右键→git bash here git init添加gitignore vi .gitignoregitignore里的内容根据自己实际情况设置,这里举个例子 # #开头的是注释 # Prer…...

统计学-R语言-7.3
文章目录 前言总体方差的检验一个总体方差的检验两个总体方差比的检验 非参数检验总体分布的检验正态性检验的图示法Shapiro-Wilk和K-S正态性检验总体位置参数的检验 练习 前言 本篇文章继续对总体方差的检验进行介绍。 总体方差的检验 一个总体方差的检验 在生产和生活的许多…...
在Idea中使用git查看历史版本
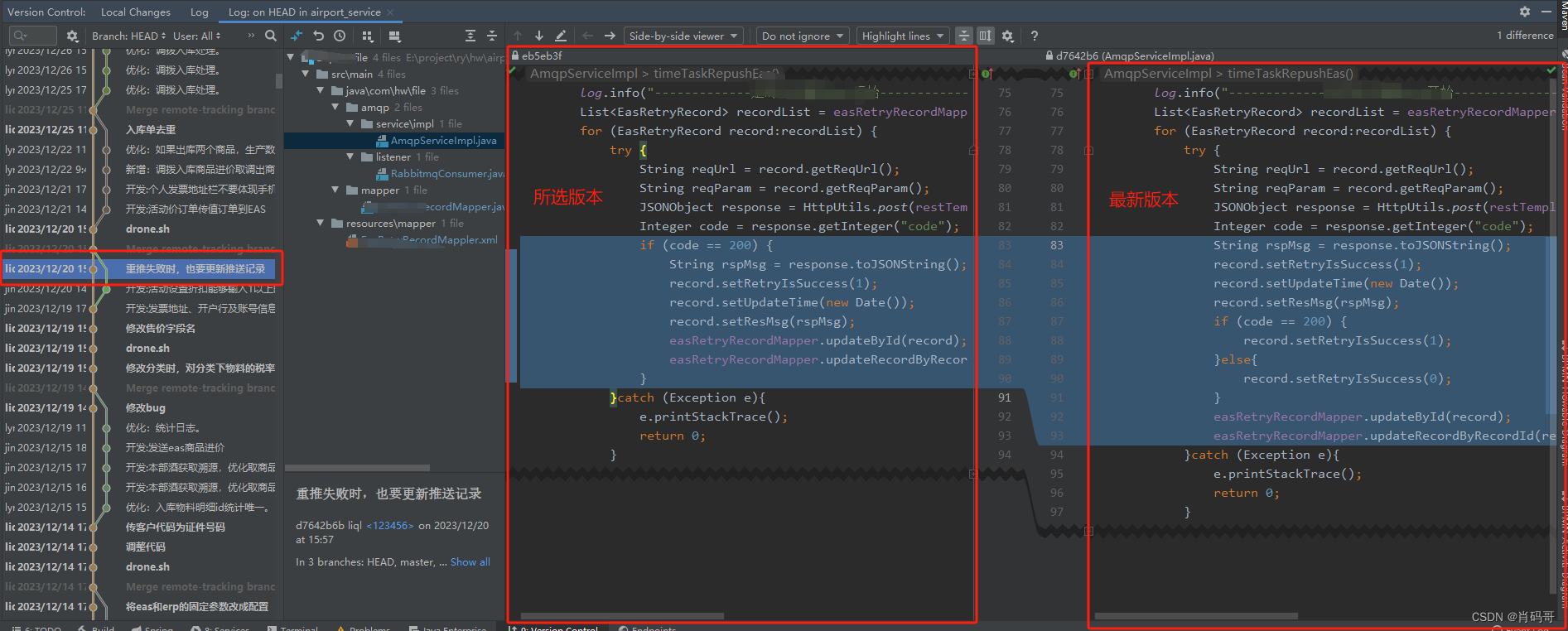
idea查git历史 背景查看步骤总结 背景 有好几次同事到我电脑用idea查看git管理的历史记录,每次都说我的idea看不了历史版本,叫我到他电脑上去看,很晕,为什么,原来是我自己把显示历史文件的视图覆盖了,下面我们来一起学…...

书籍 - 《华杉讲透孙子兵法》 - 11
第十章 地形第十 六种地形的用兵之道(一):先占有利地形 我们读兵法,会发现很多时候,等待都是最好的策略。你一定要懂得等,等得起。有的人不能等,总以为等待就是不作为,那就容易“胡作…...

2024 axios封装 包括请求拦截、错误码等
1.新建 codeMessage.ts export default {200: "服务器成功返回请求的数据。",201: "新建或修改数据成功。",202: "一个请求已经进入后台排队(异步任务)。",204: "删除数据成功。",400: "发出的请求有错误…...

Kotlin Multiplatform项目推荐 | 太空人分布图
Kotlin Multiplatform项目推荐 | 太空人分布图 项目简介 Kotlin Multiplatform项目是一种跨平台开发技术,它可以同时使用SwiftUI、Jetpack Compose、Compose for Wear OS、Compose for Desktop、Compose for Web、Kotlin/JS React等客户端框架,并且使…...
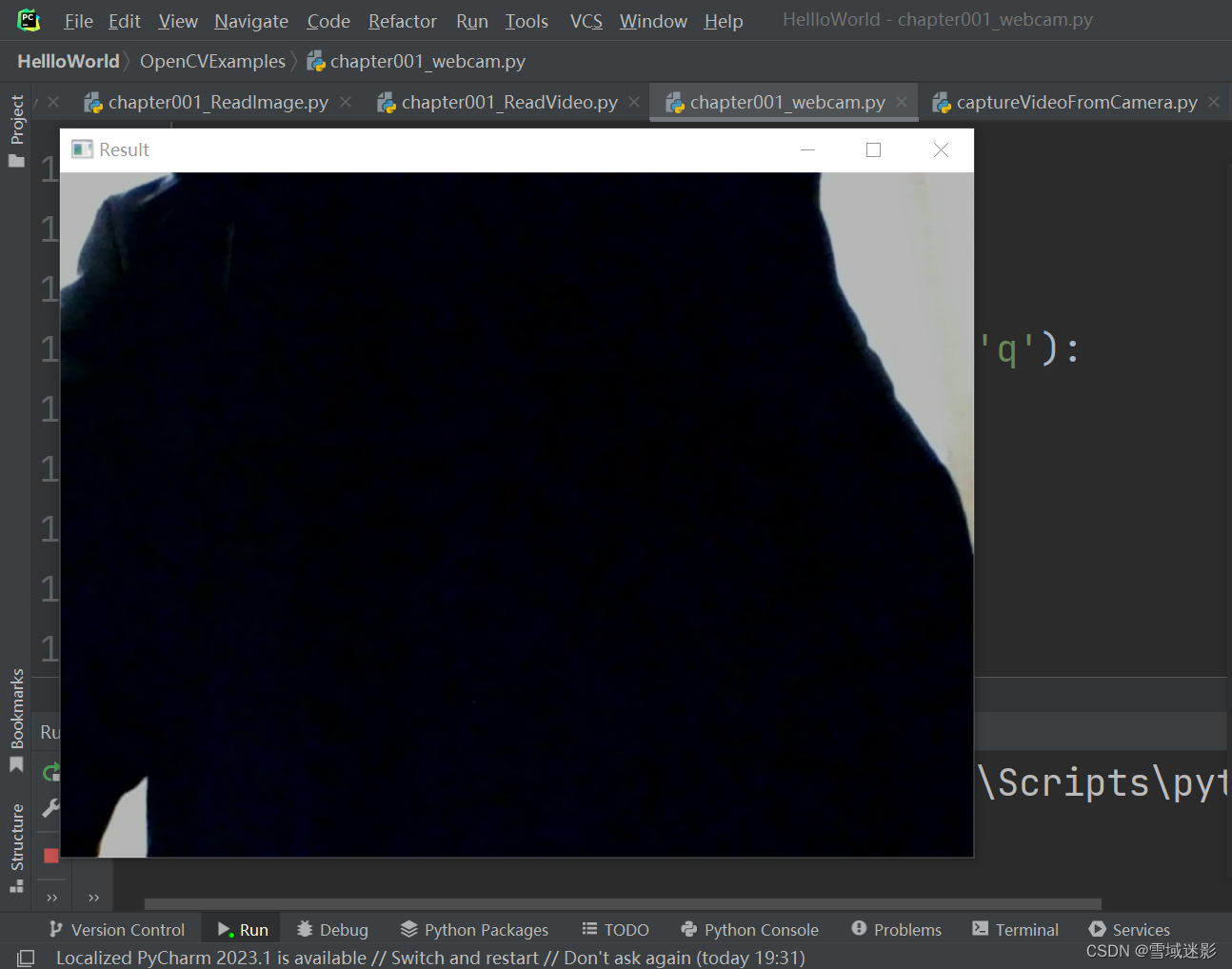
使用Opencv-python库读取图像、本地视频和摄像头实时数据
使用Opencv-python库读取图像、本地视频和摄像头实时数据 Python中使用OpenCV读取图像、本地视频和摄像头数据很简单, 首先需要安装Python,然后安装Opencv-python库 pip install opencv-python然后在PyCharm或者VScode等IDE中输入对应的Python代码 一…...
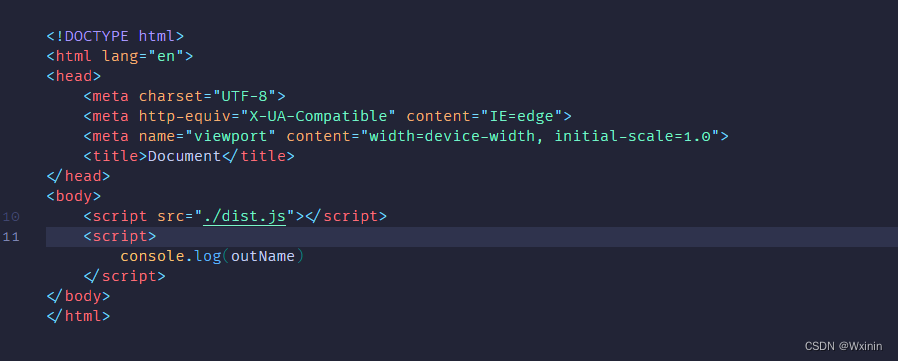
webpack如何把dist.js中某个模块js打包成一个全局变量,使得在html引入dist.js后可以直接访问
webpack可以通过使用expose-loader来将模块中的一个js文件暴露为全局可以访问的变量。下面是一个示例代码: 1、安装expose-loader npm install expose-loader --save-dev 2、webpack.config.js配置文件 值得注意的是:我在本地使用16.14.2版本的node打包…...
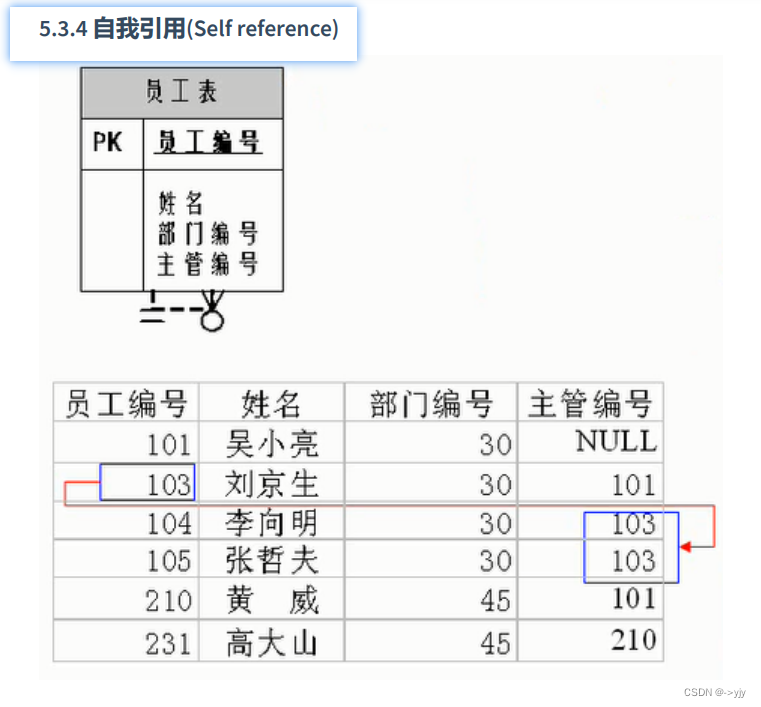
Mysql第一天
数据库概述 1. 为什么要使用数据库 持久化(persistence):把数据保存到可掉电式存储设备中以供之后使用。(可掉电:内存 使用高电压和低电压来区别0和1进行数据的一个存储但是一旦断电了电压都没了 0和1也就没有了)大多数情况下,特别是企 业级应用&#…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

OCC笔记:TDF_Label中有多个相同类型属性
注:OCCT版本:7.9.1 TDF_Label中有多个相同类型的属性的方案 OCAF imposes the restriction that only one attribute type may be allocated to one label. It is necessary to take into account the design of the application data tree. For exampl…...

Ansys Maxwell:线圈和磁体的静磁 3D 分析
本博客展示了如何在 Ansys Maxwell 中执行静磁 3D 分析,以计算载流线圈和永磁体之间相互作用产生的扭矩。在这个例子中,线圈中的电流产生一个沿 Y 轴指向的磁场,而永磁体沿 X 轴被磁化。这种配置导致围绕 Z 轴的扭矩。分步工作流程包括构建几…...
