【leetcode题解C++】150.逆波兰表达式求值 and 239.滑动窗口最大值 and 347.前k个高频元素
150.逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释:该算式转化为常见的中缀算术表达式为:((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22
思路: 注意到,后序表达式,那么用栈,遇到数字就压入栈,遇到运算符就取两个数字出来运算,得到ans压入栈,继续循环直到没有元素可以读取。需要注意的是,如果过只给一个数字,那么需要用top()来获取。
代码实现:
class Solution {
public:int evalRPN(vector<string>& tokens) {int ans = 0;stack<int> stk;int num1 = 0, num2 = 0;for(int i = 0; i < tokens.size(); ++i) {if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {num1 = stk.top();stk.pop();num2 = stk.top();stk.pop();if(tokens[i] == "+") ans = num2 + num1;if(tokens[i] == "-") ans = num2 - num1;if(tokens[i] == "*") ans = num2 * num1;if(tokens[i] == "/") ans = num2 / num1;stk.push(ans);}else {stk.push(stoi(tokens[i]));}}ans = stk.top();return ans;}
};239.滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 31 [3 -1 -3] 5 3 6 7 31 3 [-1 -3 5] 3 6 7 51 3 -1 [-3 5 3] 6 7 51 3 -1 -3 [5 3 6] 7 61 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1 输出:[1]
思路:读题后发现很暴力很直接,很顺畅就用一个queue和一个vector写出了暴力的解法,感叹困难题不过尔尔,提交发现超时...真是事与愿违,后面学到了单调队列,用一个队列,维护队首的元素永远是最大的(下面维护的是下标),首先处理最前面k个元素,然后初始化需要返回的vector,然后再处理后面的元素,直到读取到最后一个元素。
代码实现:
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {deque<int> deq;for(int i = 0; i < k; ++i) {while(!deq.empty() && nums[i] >= nums[deq.back()]) {deq.pop_back();}deq.push_back(i);}vector<int> ans = {nums[deq.front()]};for(int i = k; i < nums.size(); ++i) {while(!deq.empty() && nums[i] >= nums[deq.back()]) {deq.pop_back();}deq.push_back(i);while(deq.front() <= i - k) {deq.pop_front();}ans.push_back(nums[deq.front()]);}return ans;}
};347.前k个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2 输出: [1,2]
示例 2:
输入: nums = [1], k = 1 输出: [1]
思路:?直~~接返回二维数组,先用个哈希map来记录每个元素的出现次数,然后加入到二维数组中,sort()一下,需要个排序的条件?甩个lambda表达式,ok排完序了,建一个vector来把前k个结果接出去。
代码实现:
class Solution {
public:vector<int> topKFrequent(vector<int>& nums, int k) {unordered_map<int, int> map;for(int i = 0; i < nums.size(); ++i) {++map[nums[i]];}vector<vector<int>> vec;for(auto& [x, y] : map) {vec.push_back({x, y});}sort(vec.begin(), vec.end(), [](const vector<int>& a, const vector<int>& b) {return a[1] > b[1];});vector<int> res;for(int i = 0; i < k && i < vec.size(); ++i) {res.push_back(vec[i][0]);}return res;}
};相关文章:

【leetcode题解C++】150.逆波兰表达式求值 and 239.滑动窗口最大值 and 347.前k个高频元素
150.逆波兰表达式求值 给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。 请你计算该表达式。返回一个表示表达式值的整数。 注意: 有效的算符为 、-、* 和 / 。每个操作数(运算对象)都可以是一个整数…...
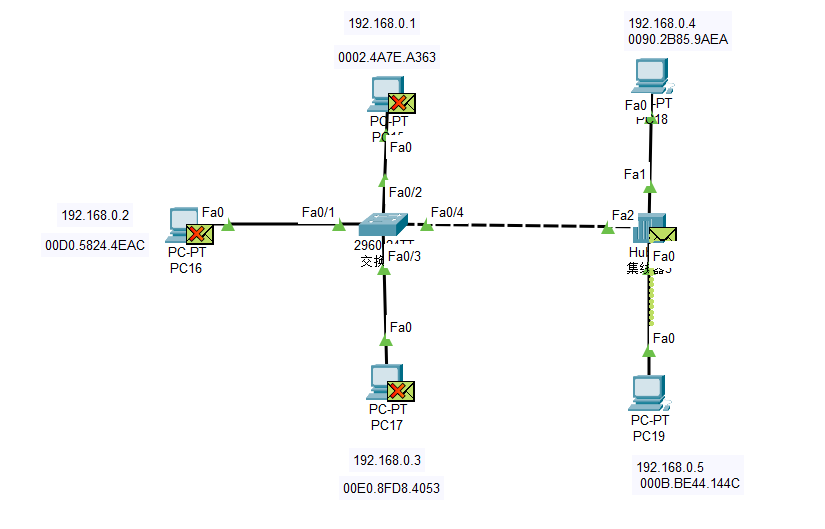
【计网·湖科大·思科】实验三 总线型以太网的特性、集线器和交换机的区别、交换机的自学习算法
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的很重要&…...

API设计模式:REST、GraphQL、gRPC与tRPC全面解析
一、引言 在现代Web和微服务架构中,API(应用程序编程接口)的设计和实现方式至关重要。本文将探讨四种流行的API设计模式:REST(Representational State Transfer)、GraphQL、gRPC以及新兴的tRPC。每种模式都…...

C/C++ protobuf与json互转
测试环境 ubuntu16.04 64bitprotocbuf:3.9.1 (支持json转换需>3.0.0) 协议 syntax "proto2";message Person{optional string name 1;optional uint32 age 2;optional string address 3; }测试代码 //protobuf > 3.0.0#…...
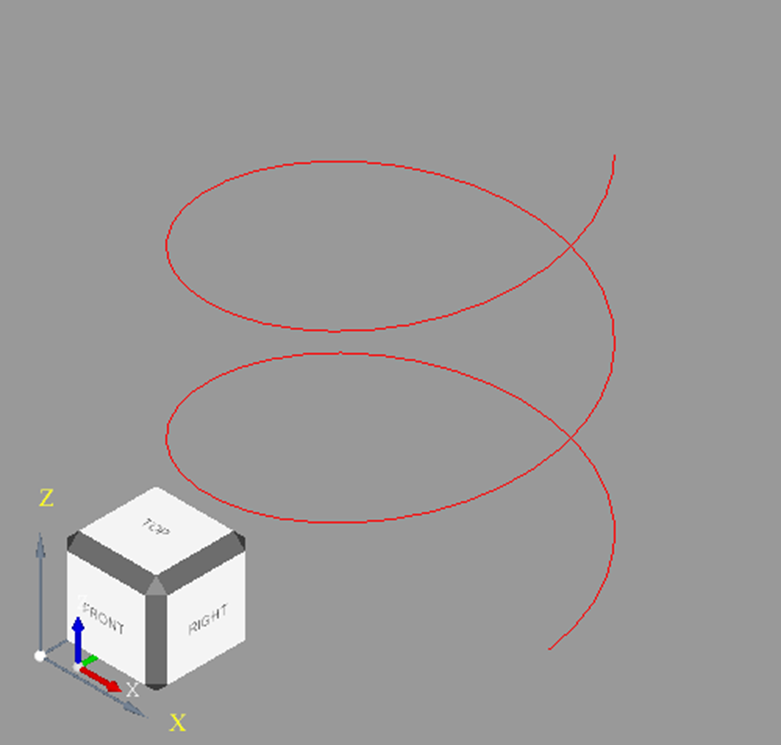
Open CASCADE学习|圆柱螺旋线绘制原理探究
1、圆柱螺旋线绘制原理 在OCC中,圆柱面的参数方程为: 设P为(x0,y0,z0),则 xx0r*cos(u) yy0r*sin(u) zz0v 但u、v之间有关系时,此方程表达为圆柱螺旋线,u、v之间为线性关系时是等螺距螺旋线࿰…...

Python学习笔记--认识sys.argv
sys.argv 是 Python 的一个内置模块 sys 中的一个属性。它是一个列表,包含了从命令行传递给脚本的参数。 例如,如果你有一个名为 script.py 的脚本,并且你从终端窗口命令行这样运行它: >>>python script.py arg1 arg2 …...
【C++】入门基础
前言:C是在C的基础之上,容纳进去了面向对象编程思想,并增加了许多有用的库,以及编程范式等。熟悉C语言之后,对C学习有一定的帮助,因此从今天开始们将进入C的学习。 💖 博主CSDN主页:…...
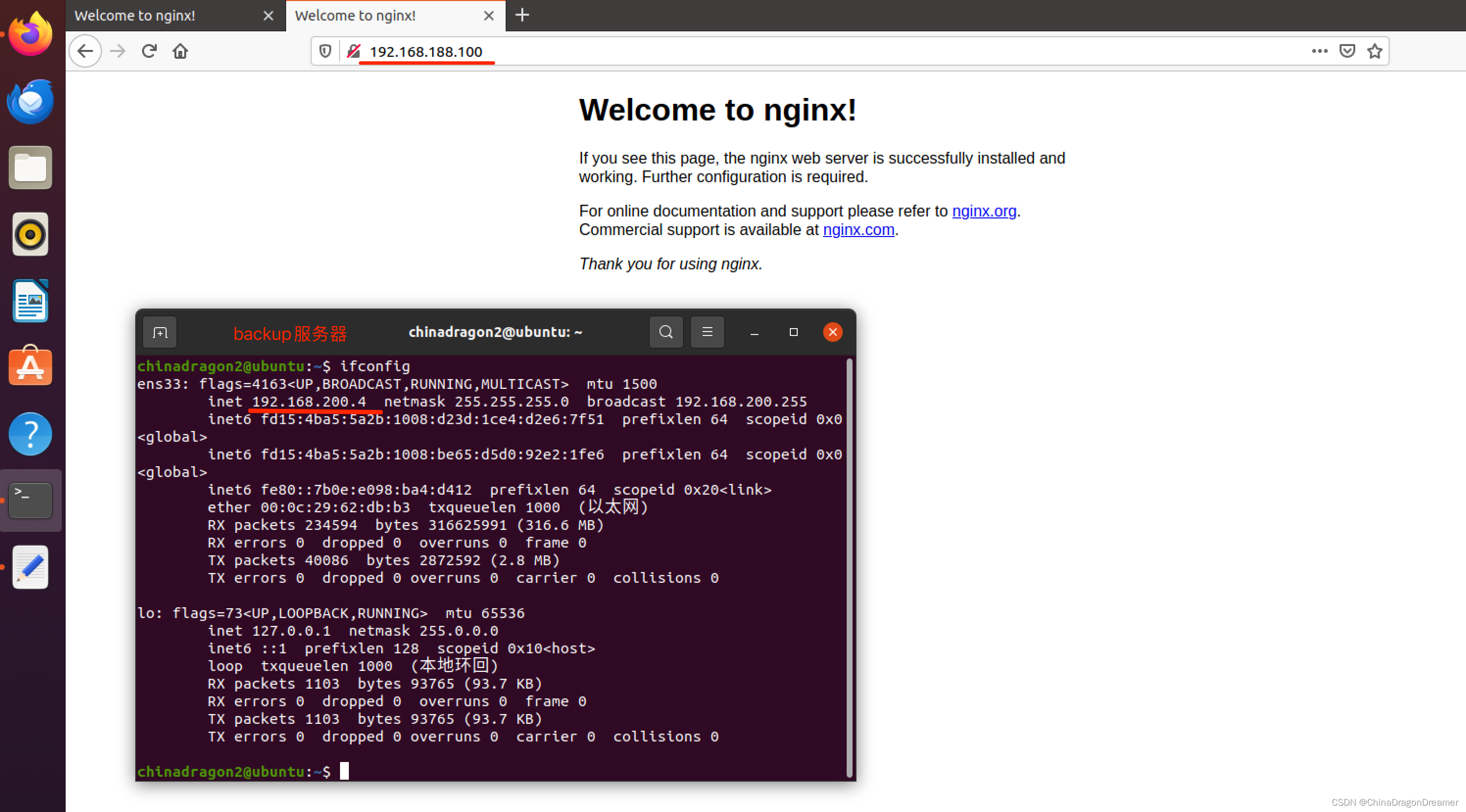
Nginx与keepalived实现集群
提醒一下:下面实例讲解是在mac虚拟机里的Ubuntu系统演示的; Nginx与keepalived实现集群实现的效果 两台服务器都安装Nginx与keepalived: master服务器的ip(192.168.200.2) backup服务器的ip(192.168.200.4) 将 master服务器Nginx与keepalive…...

初识MQRabbitMQ快速入门
一、同步和异步通讯 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,需要实时响应。 异步通讯:就像发邮件,不需要马上回复。 两种方式各有优劣,打电话可以立即得到响应,但是你却不能…...

javaMailSender 发送邮件,基于Spring Boot
目录 引入依赖 配置文件配置 具体代码 MultipartFile 转 File 工具类 引入依赖 <!--邮件--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId></dependency><!--日…...

【汇总】解决Spring-Web与Spring-WebFlux冲突
【汇总】解决Spring-Web与Spring-WebFlux冲突 问题发现问题解决问题一:The bean requestMappingHandlerMapping, defined in class path resource [org/springframework/web/reactive/config/DelegatingWebFluxConfiguration.class],问题二:The Java/XML…...

maven 依赖配置补充
依赖配置补充 依赖范围 import 管理依赖最基本的办法是继承父工程,但是和 Java 类一样,Maven 也是单继承的。如果不同体系的依赖信息封装在不同 POM 中了,没办法继承多个父工程怎么办?这时就可以使用 import 依赖范围。 典型案…...

Pandas ------ 向 Excel 文件中写入含有合并表头的数据
Pandas ------ 向 Excel 文件中写入含有合并表头的数据 推荐阅读引言正文 推荐阅读 Pandas ------ 向 Excel 文件中写入含有 multi-index 和 Multi-column 表头的数据 引言 这里给大家介绍一下如何向 Excel 中写入带有合并表头的数据。 正文 import pandas as pddf1 pd.D…...
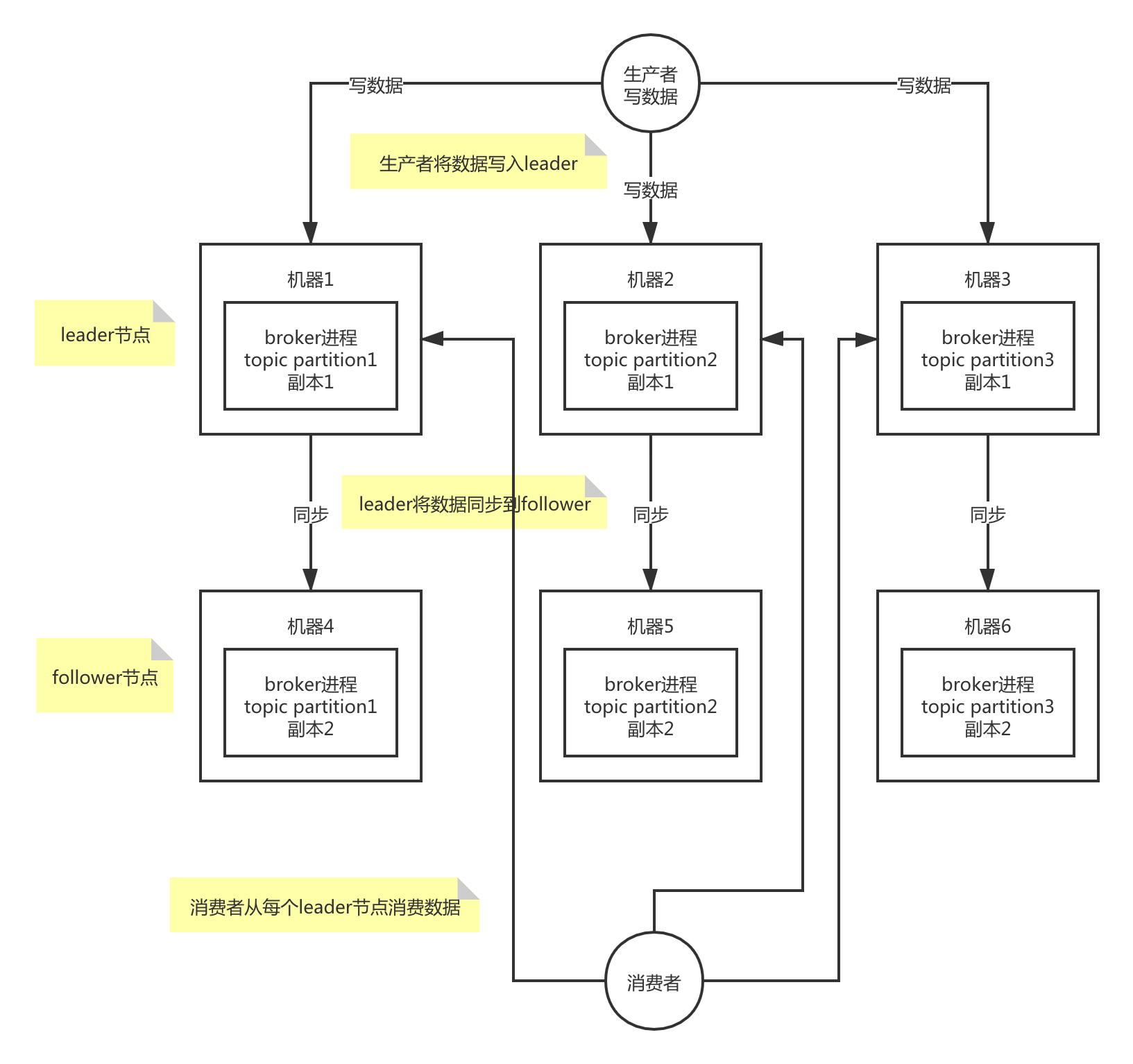
kafka summary
最近整体梳理之前用到的一些东西,回顾Kafka的时候好多东西都忘记了,把一些自己记的比较模糊并且感觉有用的东西整理一遍并且记忆一遍,仅用于记录以备后续回顾 Kafka的哪些场景中使用了零拷贝 生产者发送消息:在 Kafka 生产者发送…...
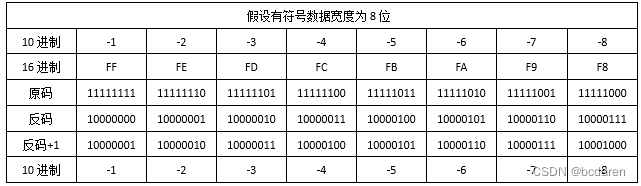
【新书推荐】2.6节 原码、反码和补码
回顾上一节中,我们讲解了整数的编码规则。 无符号整数编码规则:无符号整数全部都是正数,是什么就存什么。 有符号整数编码规则:有符号整数最高有效位为0是正数,最高有效位为1是负数。 本节内容:原码、反…...
docker 网络及如何资源(CPU/内存/磁盘)控制
安装Docker时,它会自动创建三个网络,bridge(创建容器默认连接到此网络)、 none 、host docker网络模式 Host 容器与宿主机共享网络namespace,即容器和宿主机使用同一个IP、端口范围(容器与宿主机或其他使…...
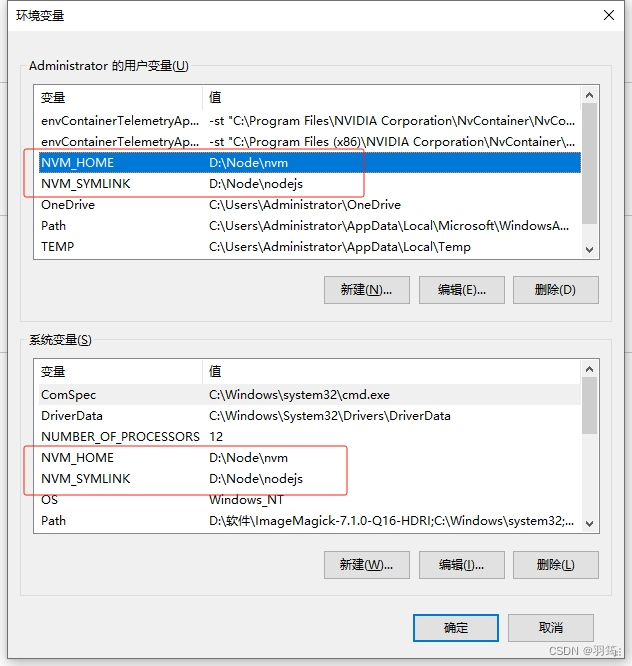
安装 nvm
前言: nvm 即 node 版本管理工具 (node version manager),好处是方便切换 node.js 版本。 通过将多个 node 版本安装在指定路径,然后通过 nvm 命令切换时,就会切换我们环境变量中 node 命令指定的实际执行的软件路径。 使用场景…...

Redis解决方案:NOAUTH Authentication required(连接jedis绑定密码或修改redis密码)
Redis解决方案:NOAUTH Authentication required(连接jedis绑定密码或修改redis密码) Java使用jedis连接redis时出现错误NOAUTH Authentication required 一、问题报错和原因 本地设置了redis的密码,但在远程连接时并没有输入密…...

多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测
多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测 目录 多维时序 | Matlab实现WOA-TCN-Multihead-Attention鲸鱼算法优化时间卷积网络结合多头注意力机制多变量时间序列预测效果一览基本介绍程序设计参考资料 效…...

如何实现无公网IP实现远程访问MongoDB文件数据库
📑前言 本文主要是如何实现无公网IP实现远程访问MongoDB文件数据库的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 &#x…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
