洛谷B3625迷宫寻路
迷宫寻路
题目描述
机器猫被困在一个矩形迷宫里。
迷宫可以视为一个 n × m n\times m n×m 矩阵,每个位置要么是空地,要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。
机器猫初始时位于 ( 1 , 1 ) (1, 1) (1,1) 的位置,问能否走到 ( n , m ) (n, m) (n,m) 位置。
输入格式
第一行,两个正整数 n , m n,m n,m。
接下来 n n n 行,输入这个迷宫。每行输入一个长为 m m m 的字符串,# 表示墙,. 表示空地。
输出格式
仅一行,一个字符串。如果机器猫能走到 ( n , m ) (n, m) (n,m),则输出 Yes;否则输出 No。
样例 #1
样例输入 #1
3 5
.##.#
.#...
...#.
样例输出 #1
Yes
提示
样例解释
路线如下: ( 1 , 1 ) → ( 2 , 1 ) → ( 3 , 1 ) → ( 3 , 2 ) → ( 3 , 3 ) → ( 2 , 3 ) → ( 2 , 4 ) → ( 2 , 5 ) → ( 3 , 5 ) (1,1)\to (2,1) \to (3,1) \to (3,2)\to (3,3) \to (2, 3) \to (2, 4) \to (2, 5) \to (3, 5) (1,1)→(2,1)→(3,1)→(3,2)→(3,3)→(2,3)→(2,4)→(2,5)→(3,5)
数据规模与约定
对于 100 % 100\% 100% 的数据,保证 1 ≤ n , m ≤ 100 1 \leq n, m \leq 100 1≤n,m≤100,且 ( 1 , 1 ) (1,1) (1,1) 和 ( n , m ) (n, m) (n,m) 均为空地。
运用bfs来解决
一开始机器猫在(0,0)位置,要走到(n-1,m-1)位置
边界条件:x、y大于0且分别小于n、m,每一点都只能走一次(通过bool数组记载是否走过),下一次要走的位置上不是#。
#include<bits/stdc++.h>
using namespace std;int n,m;
const int N = 110;
char path[N][N];
bool st[N][N];
int X[4] = {-1,0,1,0};
int Y[4] = {0,-1,0,1};bool bfs()
{//BFS使用一个队列来存储待访问的节点。//队列的特性是先进先出(FIFO),这确保了BFS是逐层访问节点的。queue<pair<int,int>> q;//创建一个队列来存储待访问节点q.push({0,0});//将起始节点(0,0)入队st[0][0] = true;//标记起始节点为已访问while(!q.empty())//当队列不为空时,继续搜索{int x = q.front().first;//取出队列中的第一个节点的坐标int y = q.front().second;q.pop();//弹出队列中的第一个节点if(x == n-1 && y == m-1)//如果当前节点是目标节点,则返回 true{return true;}//遍历当前节点的四个相邻方向for(int i = 0;i < 4;i++){int dx = x + X[i];//计算新节点的 x 坐标int dy = y + Y[i];//计算新节点的 y 坐标//检查新节点是否在网格范围内、是否未被访问过、以及是否是可通过的节点if(dx >= 0 && dy >= 0 && dx < n&& dy < m && !st[dx][dy] && path[dx][dy] != '#'){st[dx][dy] = true;//标记新节点为已访问q.push({dx,dy});//将新节点加入队列,以便后续访问它的相邻节点}}}return false;//如果队列为空且没有找到目标节点,则返回 false
}int main()
{cin >> n >> m;for(int i = 0;i < n;i++){for(int j = 0;j < m;j++){cin >> path[i][j];st[i][j] = false;}}if(bfs()){cout << "Yes" <<endl;}else{cout << "No" <<endl;}return 0;
}扩展
获取单一行走路径:
#include<bits/stdc++.h>
using namespace std;int n, m;
const int N = 110;
char path[N][N];
bool st[N][N];
pair<int, int> previous[N][N]; // 用于记录每个节点的父节点
int X[4] = {-1, 0, 1, 0};
int Y[4] = {0, -1, 0, 1};bool bfs() {queue<pair<int, int>> q;q.push({0, 0});st[0][0] = true;while (!q.empty()) {int x = q.front().first;int y = q.front().second;q.pop();if (x == n - 1 && y == m - 1) {return true; // 找到目标节点,返回true表示找到路径}for (int i = 0; i < 4; i++) {int dx = x + X[i];int dy = y + Y[i];if (dx >= 0 && dy >= 0 && dx < n && dy < m && !st[dx][dy] && path[dx][dy] != '#') {st[dx][dy] = true;previous[dx][dy] = {x, y}; // 记录父节点q.push({dx, dy});}}}return false; // 无法到达目标节点
}void printPath() {int x = n - 1, y = m - 1;vector<pair<int, int>> path;// 回溯到起点,构建路径while (x != 0 || y != 0) {path.push_back({x, y});pair<int, int> p = previous[x][y];x = p.first;y = p.second;}path.push_back({0, 0}); // 添加起点// 打印路径(从起点到终点)for (int i = path.size() - 1; i >= 0; i--) {cout << "(" << path[i].first << "," << path[i].second << ") ";}cout << endl;
}int main() {cin >> n >> m;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {cin >> path[i][j];st[i][j] = false;previous[i][j] = {-1, -1}; // 初始化为无效值}}if (bfs()) {cout << "Yes" << endl;printPath(); // 打印路径} else {cout << "No" << endl;}return 0;
}在这段代码中,增加了一个previous数组来记录每个节点的父节点。当找到目标节点时,bfs函数返回true,然后调用printPath函数来回溯并打印出从起点到终点的路径。
bfs部分详解:
void printPath() { int x = n - 1, y = m - 1; // 从终点开始回溯 vector<pair<int, int>> path; // 用于存储路径上的节点坐标 // 回溯到起点,构建路径 while (x != 0 || y != 0) { // 当还没有回溯到起点时继续循环 path.push_back({x, y}); // 将当前节点坐标添加到路径中 pair<int, int> p = previous[x][y]; // 获取当前节点的父节点坐标 x = p.first; // 更新x坐标为父节点的x坐标 y = p.second; // 更新y坐标为父节点的y坐标 } path.push_back({0, 0}); // 添加起点到路径中,因为上面的循环条件导致起点不会被添加 // 打印路径(从起点到终点),注意这里是从后往前打印,因为路径是从起点开始记录的 for (int i = path.size() - 1; i >= 0; i--) { cout << "(" << path[i].first << "," << path[i].second << ") "; // 打印每个节点的坐标 } cout << endl; // 打印换行
}
printPath 函数是用于打印从起点(0,0)到终点(n-1, m-1)在迷宫中的具体路径的。这个函数通过回溯的方式,利用在广度优先搜索(BFS)过程中记录的每个节点的父节点信息,来重建整条路径。
这个函数的工作流程如下:
- 初始化终点坐标
(x, y)为(n-1, m-1)。 - 创建一个空的
vector容器path,用于存储路径上的节点坐标。 - 使用
while循环进行回溯,条件是当前节点不是起点(即x != 0 || y != 0)。- 在循环中,首先将当前节点的坐标
(x, y)添加到path中。 - 然后,通过查询
prev数组获取当前节点的父节点坐标,并将父节点坐标赋值给(x, y),以便在下一次循环中继续回溯。
- 在循环中,首先将当前节点的坐标
- 循环结束后,将起点坐标
(0, 0)添加到path中,因为回溯过程是从终点开始,到起点结束,但由于循环条件的限制,起点并未被包含在内,所以需要手动添加。 - 最后,使用
for循环逆序打印path中的节点坐标。这是因为路径在path中是以从终点到起点的顺序存储的,而我们需要按照从起点到终点的顺序打印出来。
通过这个函数,我们就可以在控制台上看到从起点到终点的完整路径了。
相关文章:

洛谷B3625迷宫寻路
迷宫寻路 题目描述 机器猫被困在一个矩形迷宫里。 迷宫可以视为一个 n m n\times m nm 矩阵,每个位置要么是空地,要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。 机器猫初始时位于 ( 1 , 1 ) (1, 1) (1,1) 的位置,问能否…...
GPT-SoVITS 测试
开箱直用版(使用 AutoDL) step1 打开地址 https://www.codewithgpu.com/i/RVC-Boss/GPT-SoVITS/GPT-SoVITS-Official 选择 AutoDL创建实例,选择 3080ti 机器 step2 创建好实例之后,进入命令行,输入命令 echo {}>…...
人工智能:更多有用的 Python 库
目录 前言 推荐 JupyterLab 入门 复杂的矩阵运算 其它人工智能和机器学习的 Python 库 前言 在这篇文章中,我们将了解更多的矩阵操作,同时再介绍几个人工智能 Python 库。 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂&#x…...

Linux BIO如何下发到HDD?
在Linux操作系统中,当创建一个Block I/O请求(BIO)时,它会被封装成适合硬件交互的数据结构,并通过内核存储子系统传递到对应的硬件控制器上,如SAS(Serial Attached SCSI)HBAÿ…...

《动手学深度学习(PyTorch版)》笔记4.6
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过。…...

Hadoop-MapReduce-源码跟读-客户端篇
一、源码下载 下面是hadoop官方源码下载地址,我下载的是hadoop-3.2.4,那就一起来看下吧 Index of /dist/hadoop/core 二、从WordCount进入源码 用idea将源码加载进来后,找到org.apache.hadoop.examples.WordCount类(快捷方法&…...
《游戏-03_3D-开发》之—新输入系统人物移动攻击连击
本次修改unity的新输入输出系统。本次修改unity需要重启,请先保存项目, 点击加号起名为MyCtrl, 点击加号设置为一轴的, 继续设置W键, 保存 生成自动脚本, 修改MyPlayer代码: using UnityEngine;…...
滴水逆向三期笔记与作业——02C语言——10 Switch语句反汇编
滴水逆向三期笔记与作业——02C语言——10 Switch语句反汇编 一、Switch语句1、switch语句 是if语句的简写2、break加与不加有什么特点?default语句可以省略吗?3、游戏中的switch语句(示例)4、添加case后面的值,一个一个增加&…...
燃烧的指针(三)
🌈个人主页:小田爱学编程 🔥 系列专栏:c语言从基础到进阶 🏆🏆关注博主,随时获取更多关于c语言的优质内容!🏆🏆 😀欢迎来到小田代码世界~ &#x…...

微服务架构实施攻略:如何选择合适的微服务通信机制?
随着业务的快速发展和系统的日益复杂,传统的单体应用逐渐显露出瓶颈,已无法满足现代软件研发的需求。微服务架构作为一种灵活、可扩展的解决方案,通过将复杂系统拆分为一系列小型服务来提高系统的可伸缩性、灵活性和可维护性。在实施微服务架…...
【jetson笔记】解决vscode远程调试qt.qpa.xcb: could not connect to display报错
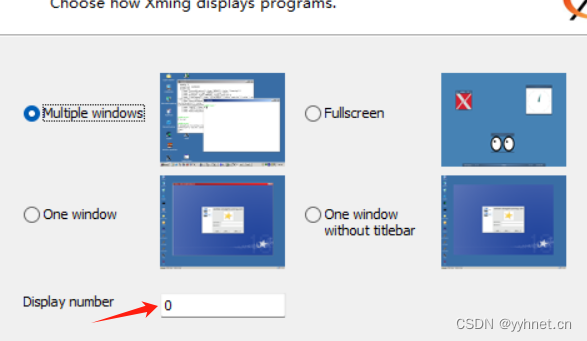
配置x11转发 jetson远程安装x11转发 安装Xming Xming下载 安装完成后打开安装目录C:\Program Files (x86)\Xming 用记事本打开X0.hosts文件,添加jetson IP地址 后续IP改变需要重新修改配置文件 localhost 192.168.107.57打开Xlaunch Win菜单搜索Xlaundch打开 一…...

网络安全产品之认识安全隔离网闸
文章目录 一、什么是安全隔离网闸二、安全隔离网闸的主要功能三、安全隔离网闸的工作原理四、安全隔离网闸的分类五、安全隔离网闸与防火墙的区别四、安全隔离网闸的应用场景 随着互联网的发展,网络攻击和病毒传播的方式越来越复杂,对网络安全的要求也越…...
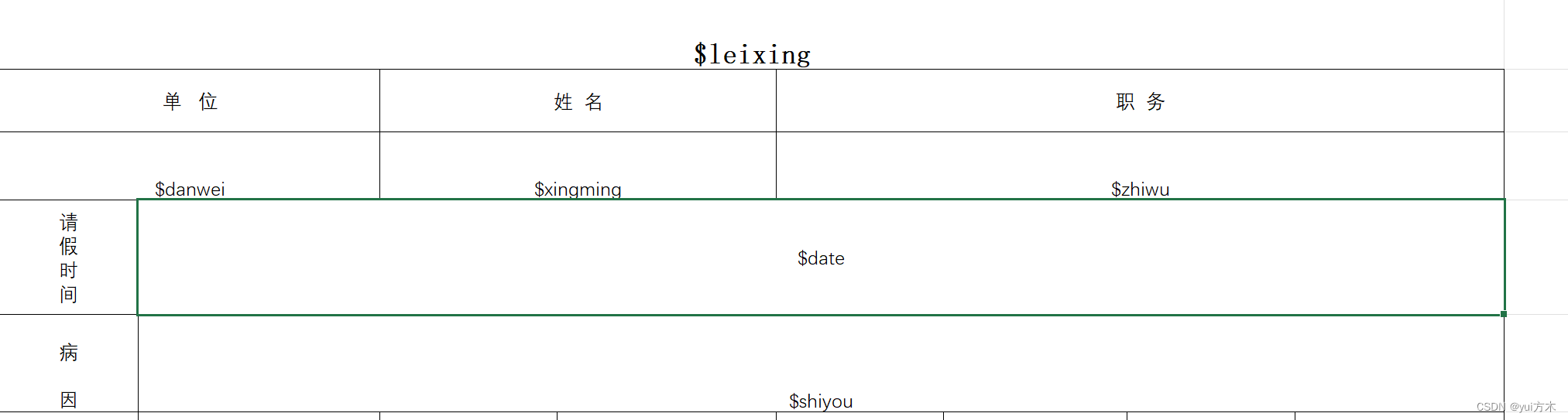
Java通过模板替换实现excel的传参填写
以模板为例子 将上面$转义的内容替换即可 package com.gxuwz.zjh.util;import org.apache.poi.ss.usermodel.*; import org.apache.poi.xssf.usermodel.XSSFWorkbook; import java.io.*; import java.util.HashMap; import java.util.Map; import java.io.IOException; impor…...
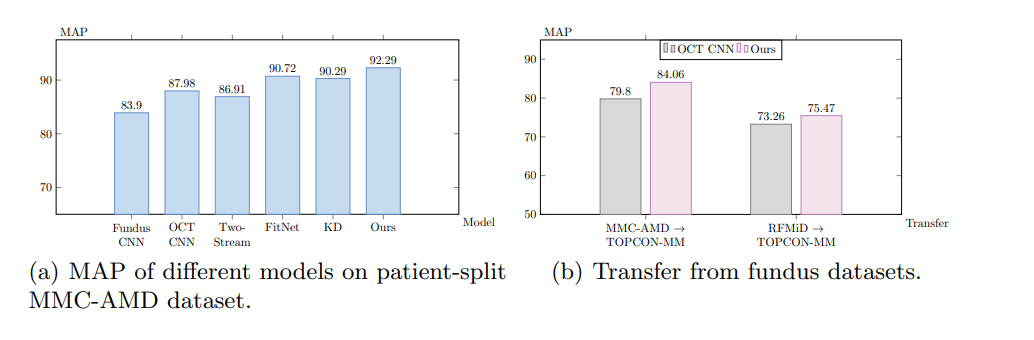
眼底增强型疾病感知蒸馏模型 FDDM:无需配对,fundus 指导 OCT 分类
眼底增强型疾病感知蒸馏模型 FDDM:fundus 指导 OCT 分类 核心思想设计思路训练和推理 效果总结子问题: 疾病特定特征的提取与蒸馏子问题: 类间关系的理解与建模 核心思想 论文:https://arxiv.org/pdf/2308.00291.pdf 代码:https://github.c…...
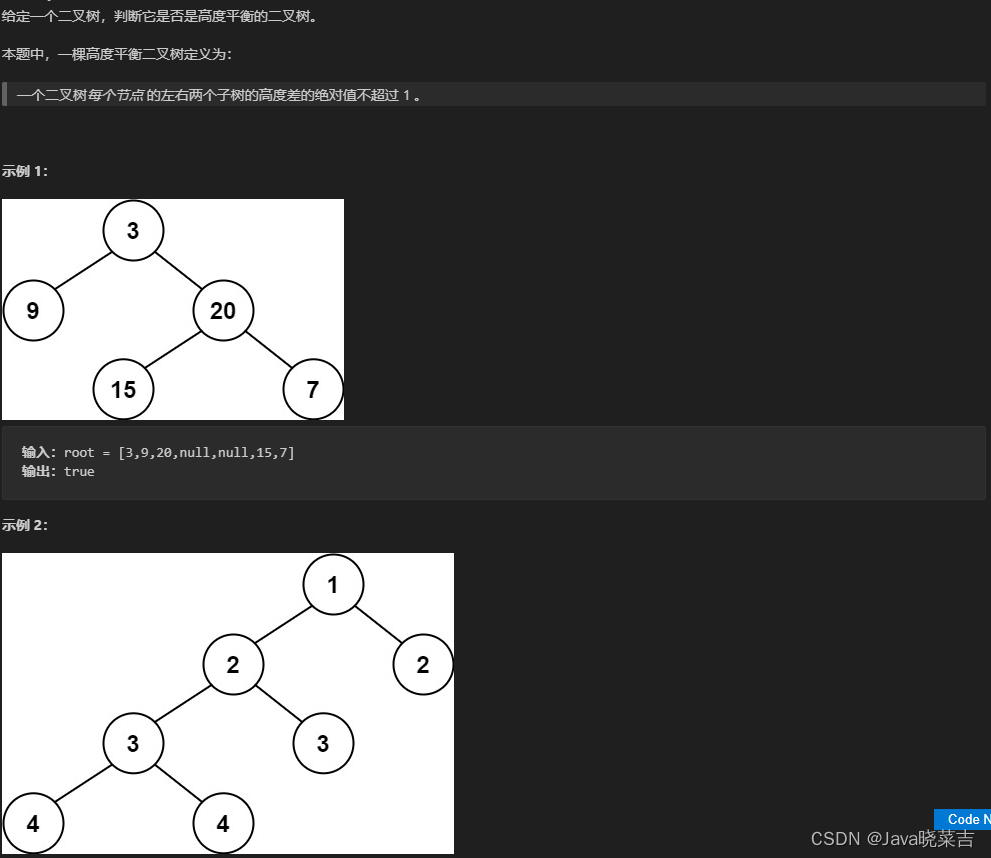
代码随想录算法刷题训练营day17
代码随想录算法刷题训练营day17:LeetCode(110)平衡二叉树 LeetCode(110)平衡二叉树 题目 代码 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(…...

Java集合如何选择
为什么使用集合 当需要存储一组类型相同的数据时,数组是最常用且最基本的容器之一。但是,使用数组存储对象存在一些不足之处,因为在实际开发中,存储的数据类型多种多样且数量不确定。这时,Java 集合就派上用场了。与数…...
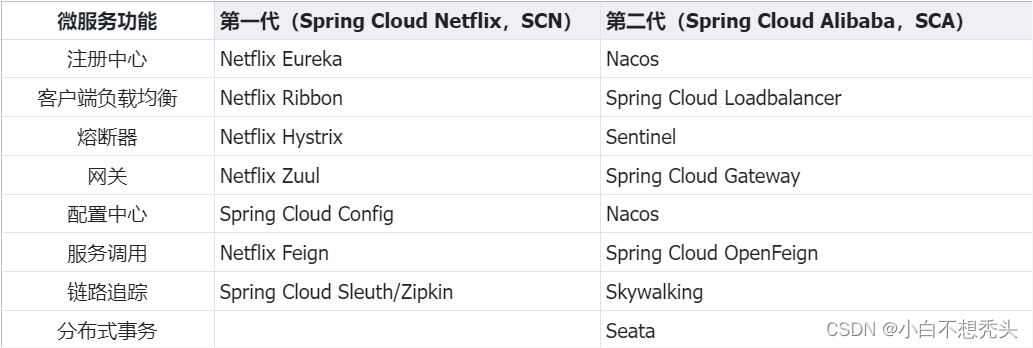
简单介绍----微服务和Spring Cloud
微服务和SpringCloud 1.什么是微服务? 微服务是将一个大型的、单一的应用程序拆分成多个小型服务,每个服务负责实现特定的业务功能,并且可以通过网络通信与其他服务通信。微服务的优点是开发更灵活(不同的微服务可以使用不同的开…...

Jenkins邮件推送配置
目录 涉及Jenkins插件: 邮箱配置 什么是授权码 在第三方客户端/服务怎么设置 IMAP/SMTP 设置方法 POP3/SMTP 设置方法 获取授权码: Jenkins配置 从Jenkins主面板System configuration>System进入邮箱配置 在Email Extension Plugin 邮箱插件…...

硬件知识(1) 手机的长焦镜头
#灵感# 手机总是配备好几个镜头,研究一下 目录 手机常配备的摄像头,及效果举例 长焦的焦距 焦距的定义和示图: IPC的焦距和适用场景: 手机常配备的摄像头,及效果举例 以下是小米某个手机的摄像头介绍:…...

华为机考入门python3--(3)牛客3-明明的随机数
分类:集合、排序 知识点: 集合添加元素 set.add(element) 集合转列表 list(set) 列表排序 list.sort() 题目来自【牛客】 N int(input().strip()) nums set()for i in range(N):nums.add(int(input().strip()))# 集合转列表 nums_list l…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
