无人机在三维空间中的转动问题
前提
这篇博客是对最近一个有关无人机拍摄图像项目中所学到的新知识的一个总结,比较杂乱,没有固定的写作顺序。
无人机坐标系旋转问题
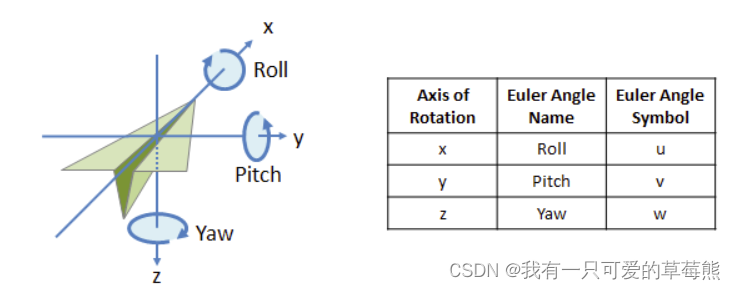
上图是无人机坐标系,绕x轴是翻滚(Roll),绕y轴是俯仰(Pitch),绕z轴是偏航(Yaw)。在初始位置,无人机坐标系和世界坐标系是对齐的,在坐标系中存在一个原始点 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0),那么当无人机翻滚、俯仰、偏航后,此时的原始点被转动到了哪个位置处?
首先是绕x轴的翻滚,翻滚角为u,旋转矩阵为:
R x ( u ) = [ 1 0 0 0 c o s ( u ) − s i n ( u ) 0 s i n ( u ) c o s ( u ) ] R_x(u)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(u) & -sin(u) \\ 0 & sin(u) & cos(u) \end{bmatrix} Rx(u)= 1000cos(u)sin(u)0−sin(u)cos(u)
可以看到,这个旋转矩阵和三维空间中某一点绕x轴旋转的旋转矩阵一样。
旋转后的坐标则为:
[ x 1 y 1 z 1 ] = R x ( u ) [ x 0 y 0 z 0 ] \begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix}= R_x(u)\begin{bmatrix} x_0 \\ y_0 \\ z_0 \end{bmatrix} x1y1z1 =Rx(u) x0y0z0
接下来是绕y轴的俯仰,俯仰角为v,旋转矩阵为:
R y ( v ) = [ c o s ( v ) 0 s i n ( v ) 0 1 0 − s i n ( v ) 0 c o s ( v ) ] R_y(v)=\begin{bmatrix} cos(v) & 0 & sin(v) \\ 0 & 1 & 0 \\ -sin(v) & 0 & cos(v) \end{bmatrix} Ry(v)= cos(v)0−sin(v)010sin(v)0cos(v)
可以看到,这个旋转矩阵和三维空间中某一点绕y轴旋转的旋转矩阵一样。
旋转后的坐标则为:
[ x 2 y 2 z 2 ] = R y ( u ) [ x 1 y 1 z 1 ] \begin{bmatrix} x_2 \\ y_2 \\ z_2 \end{bmatrix}= R_y(u)\begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix} x2y2z2 =Ry(u) x1y1z1
接下来是绕z轴的偏航,偏航角为w,旋转矩阵为:
R z ( v ) = [ c o s ( w ) − s i n ( w ) 0 s i n ( w ) c o s ( w ) 0 0 0 1 ] R_z(v)=\begin{bmatrix} cos(w) & -sin(w) & 0 \\ sin(w) & cos(w) & 0 \\ 0 & 0 & 1 \end{bmatrix} Rz(v)= cos(w)sin(w)0−sin(w)cos(w)0001
可以看到,这个旋转矩阵和三维空间中某一点绕z轴旋转的旋转矩阵一样。
旋转后的坐标则为:
[ x 3 y 3 z 3 ] = R z ( u ) [ x 2 y 2 z 2 ] \begin{bmatrix} x_3 \\ y_3 \\ z_3 \end{bmatrix}= R_z(u)\begin{bmatrix} x_2 \\ y_2 \\ z_2 \end{bmatrix} x3y3z3 =Rz(u) x2y2z2
将三个旋转矩阵结合起来就就是:
[ x 3 y 3 z 3 ] = R z ( w ) × R y ( v ) × R x ( u ) [ x 0 y 0 z 0 ] \begin{bmatrix} x_3 \\ y_3 \\ z_3 \end{bmatrix}= R_z(w)\times R_y(v)\times R_x(u)\begin{bmatrix} x_0 \\ y_0 \\ z_0 \end{bmatrix} x3y3z3 =Rz(w)×Ry(v)×Rx(u) x0y0z0
可以看到这里面有很重要的一点就是: R z ( w ) 、 R y ( v ) 、 R x ( u ) R_z(w)、R_y(v)、R_x(u) Rz(w)、Ry(v)、Rx(u)相乘时的顺序不能发生改变,一旦发生改变(矩阵相乘没有交换律),则结果也会发生变化。
对上面进行总结,整体上如下图所示:

已知在无人机坐标系下的一点 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0),求无人机在翻滚u度,俯仰v度,偏航w度后的点坐标 ( x 3 , y 3 , z 3 ) (x_3,y_3,z_3) (x3,y3,z3)。计算公式如上所示。
图像相关问题
视场角
一般来说,相机的视场角(FOV)有三个,H FOV(水平视场角)、V FOV(垂直视场角),D FOV(对角视场角),如下图所示,一目了然。

图像的单应性变换
单应性的一个不严谨定义是:用无镜头畸变的相机从不同位置拍摄同一平面物体的图像之间存在单应性,可以用透视变换表示。

也就是说,给Right view的图像上的点经过透视变换可以变到left view图像上对应位置,透视变换也就是一个矩阵,我们称之为单应性矩阵。
这里不对单应性矩阵进行详细介绍,只是说求解单应性矩阵有8个参数,因此需要四组对应点。
一种常见的方法是寻找两张图像中的相似特征点,然后用来求解单应性矩阵,参考此链接中有相关代码,以及对单应性矩阵的具体介绍。
findHomography函数和getPerspectiveTransform函数
两个函数都可以用来求单应性矩阵,结果一样。但getPerspectiveTransform只会拿四组点去计算,findHomography会拿多组点(大于等于4组)点去计算。
参考链接
- https://danceswithcode.net/engineeringnotes/rotations_in_3d/rotations_in_3d_part1.html
- https://www.sohu.com/a/657116799_121116014
- https://zhuanlan.zhihu.com/p/74597564
- https://blog.csdn.net/Sunshine_in_Moon/article/details/45478351
相关文章:

无人机在三维空间中的转动问题
前提 这篇博客是对最近一个有关无人机拍摄图像项目中所学到的新知识的一个总结,比较杂乱,没有固定的写作顺序。 无人机坐标系旋转问题 上图是无人机坐标系,绕x轴是翻滚(Roll),绕y轴是俯仰(Pitch),绕z轴是偏航(Yaw)。…...
鸿蒙开发初体验
文章目录 前言一、环境配置1.1 安装DevEco Studio1.2 安装相关环境 二、工程创建三、工程结构介绍四、代码实现4.1 初识ArkTs4.2 具体实现 参考资料 前言 HarmonyOS是华为公司推出的一种操作系统,旨在为不同设备提供统一的操作系统和开发平台。鸿蒙开发的出现为用户…...
【Axure教程0基础入门】02高保真基础
02高保真基础 1.高保真原型的要素 (1)静态高保真原型图 尺寸:严格按照截图比例,参考线 色彩:使用吸取颜色,注意渐变色 贴图:矢量图/位图,截取,覆盖等 (…...

【GitHub项目推荐--常见的国内镜像】【转载】
由于国内网络原因,下载依赖包或者软件,对于不少互联网从业者来说,都有不小的挑战,时间浪费在这上边,实在可惜。这个项目介绍了常见依赖,软件的国内镜像,助力大家畅爽编码。 这是一个归纳梳理类…...
实战 | OpenCV+OCR实现弧形文字识别实例(详细步骤 + 源码)
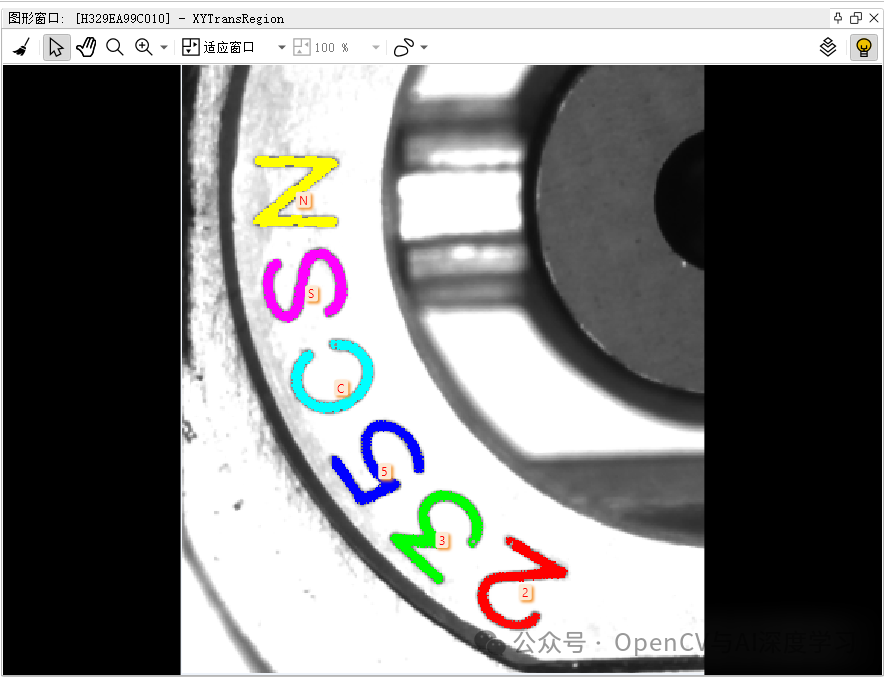
导 读 本文主要介绍基于OpenCV+OCR实现弧形文字识别实例,并给详细步骤和代码。源码在文末。 背景介绍 测试图如下,目标是正确识别图中的字符。图片来源: https://www.51halcon.com/forum.php?mod=viewthread&tid=6712 同样,论坛中已经给出了Halcon实现代码,…...
哪些 3D 建模软件值得推荐?
云端地球是一款免费的在线实景三维建模软件,不需要复杂的技巧,只要需要手机,多拍几张照片,就可以得到完整的三维模型! 无论是大场景倾斜摄影测量还是小场景、小物体建模,都可以通过云端地球将二维数据向三…...
AI论文指南|人大教授教你如何利用ChatGPT革新内容分析!【建议收藏】
点击下方▼▼▼▼链接直达AIPaperPass ! AIPaperPass - AI论文写作指导平台 公众号原文▼▼▼▼: AI论文指南|人大教授教你如何利用ChatGPT革新内容分析!【建议收藏】 目录 1.ChatGPT内容分析 2.书籍介绍 3.AIPaperPass智能论文写作平…...

leetcode 字符串相关题目
344. 反转字符串 - 力扣(LeetCode) 题解:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 541. 反转字符串 II - 力扣(LeetCode) 题解:https://leetcode.cn/problems/reverse-s…...

第二百九十一回
文章目录 1. 概念介绍2. 方法与细节2.1 实现方法2.2 具体细节 3. 示例代码4. 内容总结 我们在上一章回中介绍了"如何混合选择图片和视频文件"相关的内容,本章回中将介绍如何混合选择多个图片和视频文件.闲话休提,让我们一起Talk Flutter吧。 1…...
简化java代码:mapstruct + 策略模式
目录 目的 准备 注意 相同类型-属性名不同 实体类 映射 使用 验证-查看实现类 测试 不同类型(策略模式) 实体类 映射 工具类 使用:对象拷贝 验证-查看实现类 测试 使用:集合拷贝 测试 策略模式说明 准备-依赖 目的 简化 BeanUtils.…...

【Java】SpringMVC路径写法
1、多级路径 ✅类路径和方法路径都可以写成多级 ✅其中,类路径写在方法路径前面 ✅与Servlet不同,SpringMVC中写不写“/”都可以 RequestMapping("/hello/t1") RestController public class HelloSpring {RequestMapping( value "world…...

数据结构之生成树及最小生成树
数据结构之生成树及最小生成树 1、生成树概念2、最小生成树 数据结构是程序设计的重要基础,它所讨论的内容和技术对从事软件项目的开发有重要作用。学习数据结构要达到的目标是学会从问题出发,分析和研究计算机加工的数据的特性,以便为应用所…...

【java面试】常见问题(超详细)
目录 一、java常见问题JDK和JRE的区别是什么?Java中的String类是可变的还是不可变的?Java中的equals方法和hashCode方法有什么关系?Java中什么是重载【Overloading】?什么是覆盖【Overriding】?它们有什么区别…...

Labview for循环精讲
本文详细介绍Labview中For循环的使用方法,从所有细节让你透彻的看明白For循环是如何使用的,如果有帮助的话记得点赞加关注~ 1. For循环结构 从最简单的地方讲起,一个常用的for循环结构是由for循环结构框图、循环次数、循环计数(i)三部分组成…...

【STM32】STM32学习笔记-W25Q64简介(37)
00. 目录 文章目录 00. 目录01. SPI简介02. W25Q64简介03. 硬件电路04. W25Q64框图05. Flash操作注意事项06. 预留07. 附录 01. SPI简介 在大容量产品和互联型产品上,SPI接口可以配置为支持SPI协议或者支持I 2 S音频协议。SPI接口默认工作在SPI方式,可以…...

clickhouse数据库 使用http 方式交付查询sql
今天使用clickhouse 的HTTP 方式进行查询语句 clickhouse 服务 搭建在192.168.0.111 上面 那么我们如何快速的去查询呢 如下 我们可以使用curl 功能 或者直接在浏览器上输入对应的查询命令 如下: http://192.168.0.111:8123/userdefault&password123456&…...

深度学习-循环神经网络-RNN实现股价预测-LSTM自动生成文本
序列模型(Sequence Model) 基于文本内容及其前后信息进行预测 基于目标不同时刻状态进行预测 基于数据历史信息进行预测 序列模型:输入或者输出中包含有序列数据的模型 突出数据的前后序列关系 两大特点: 输入(输出)元素之间是具有顺序关系。不同的顺序,得到的结果应…...

案例分享 | 助力数字化转型:嘉为科技项目管理平台上线
嘉为科技项目管理平台(一期)基于易趋(EasyTrack)进行实施,通过近一年的开发及试运行,现已成功交付上线、推广使用,取得了良好的应用效果。 1.关于广州嘉为科技有限公司(以下简称嘉为…...

深入理解 MySQL 中的 HAVING 关键字和聚合函数
深入理解 MySQL 中的 HAVING 关键字和聚合函数 在处理数据库查询时,尤其是涉及到大量数据分析和报表生成的场合,了解如何有效使用 SQL 语句中的 HAVING 关键字和聚合函数变得尤为重要。 什么是 HAVING 关键字? HAVING 关键字在 SQL 语句中…...
,利弊分析)
GPT4.5人工智能即将来临,ChatGPT的正面影响和负面影响(好处和坏处),利弊分析
ChatGPT来了,对我们影响大不大? 近年来,人工智能技术的飞速进步催生了ChatGPT——一种强大的人工智能语言模型。其杰出的生成能力使其能够与人类进行自然、流畅的交流,从而在教育、医疗和娱乐等多个领域展现出巨大的应用潜力。然…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
