算法每日一题: 边权重均等查询 | 公共子祖先
大家好,我是星恒,今天给大家带来的是一道图里面有关公共子祖先的题目,理解起来简单,大家
题目:leetcode 2846
现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。另给你一个长度为 m 的二维整数数组 queries ,其中 queries[i] = [ai, bi] 。对于每条查询,请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中,你可以选择树上的任意一条边,并将其权重更改为任意值。
注意:
- 查询之间 相互独立 的,这意味着每条新的查询时,树都会回到 初始状态 。
- 从 ai 到 bi的路径是一个由 不同 节点组成的序列,从节点 ai 开始,到节点 bi 结束,且序列中相邻的两个节点在树中共享一条边。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是第 i 条查询的答案。
示例 1:
输入:n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出:[0,0,1,3]
解释:第 1 条查询,从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此,答案为 0 。
第 2 条查询,从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 0 。
第 3 条查询,将边 [2,3] 的权重变更为 2 。在这次操作之后,从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 1 。
第 4 条查询,将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后,从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
示例 2: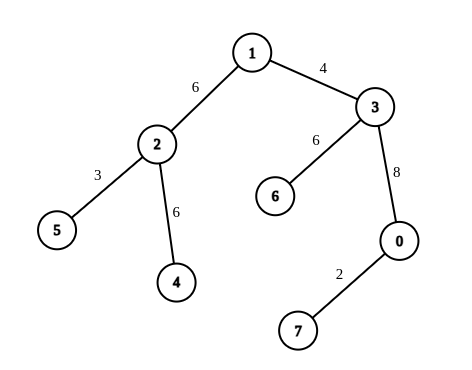
输入:n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
输出:[1,2,2,3]
解释:第 1 条查询,将边 [1,3] 的权重变更为 6 。在这次操作之后,从节点 4 到节点 6 的路径中的所有边的权重都是 6 。因此,答案为 1 。
第 2 条查询,将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后,从节点 0 到节点 4 的路径中的所有边的权重都是 6 。因此,答案为 2 。
第 3 条查询,将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后,从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此,答案为 2 。
第 4 条查询,将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后,从节点 7 到节点 4 的路径中的所有边的权重都是 6 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
提示:
- 1 <= n <= 104
- edges.length == n - 1
- edges[i].length == 3
- 0 <= ui, vi < n
- 1 <= wi <= 26
- 生成的输入满足 edges 表示一棵有效的树
- 1 <= queries.length == m <= 2 * 104
- queries[i].length == 2
- 0 <= ai, bi < n
分析:
我们先看这道题的最直接的问题,如何寻找修改最少次数?我们只需要贪心的让两个点之间所有边,变为边权重出现最多的次数的权重,例如寻找a和b两点间修改的最小次数,如果ab两点间所有边中,权重2出现的次数最多,我们就让所有边的值改为2,这样修改的次数就最少了
好,知道这一点,我们的问题就变成了寻找两点间所有权重中,哪个权重出现次数最多。我们从提示中可以看出,权重的取值范围为1 - 26,我们可以计算每个点到根节点(开始节点)的每个权重出现的次数,然后当我们计算两点之间的最小 权重出现次数 时,这样计算:
我们还是使用之前的例子,计算a - b间:
count[a][i] + count[b][i] - 2count[c][i]
- c是公共子祖先
- count[a][i] 为节点a到根节点,权重为i的边出现的次数
难点:寻找公共祖先,这个大家可以在网上了解一下,这里使用Tarjan 算法
推荐链接:https://oi.wiki/graph/lca/#tarjan-%E7%AE%97%E6%B3%95
代码:
class Solution {static final int W = 26;public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {int m = queries.length;Map<Integer, Integer>[] neighbors = new Map[n];for (int i = 0; i < n; i++) {neighbors[i] = new HashMap<Integer, Integer>();}for (int[] edge : edges) {neighbors[edge[0]].put(edge[1], edge[2]);neighbors[edge[1]].put(edge[0], edge[2]);}List<int[]>[] queryArr = new List[n];for (int i = 0; i < n; i++) {queryArr[i] = new ArrayList<int[]>();}for (int i = 0; i < m; i++) {queryArr[queries[i][0]].add(new int[]{queries[i][1], i});queryArr[queries[i][1]].add(new int[]{queries[i][0], i});}int[][] count = new int[n][W + 1];boolean[] visited = new boolean[n];int[] uf = new int[n];int[] lca = new int[m];tarjan(0, -1, neighbors, queryArr, count, visited, uf, lca);int[] res = new int[m];for (int i = 0; i < m; i++) {int totalCount = 0, maxCount = 0;for (int j = 1; j <= W; j++) {int t = count[queries[i][0]][j] + count[queries[i][1]][j] - 2 * count[lca[i]][j];maxCount = Math.max(maxCount, t);totalCount += t;}res[i] = totalCount - maxCount;}return res;}public void tarjan(int node, int parent, Map<Integer, Integer>[] neighbors, List<int[]>[] queryArr, int[][] count, boolean[] visited, int[] uf, int[] lca) {if (parent != -1) {System.arraycopy(count[parent], 0, count[node], 0, W + 1);count[node][neighbors[node].get(parent)]++;}uf[node] = node;for (int child : neighbors[node].keySet()) {if (child == parent) {continue;}tarjan(child, node, neighbors, queryArr, count, visited, uf, lca);uf[child] = node;}for (int[] pair : queryArr[node]) {int node1 = pair[0], index = pair[1];if (node != node1 && !visited[node1]) {continue;}lca[index] = find(uf, node1);}visited[node] = true;}public int find(int[] uf, int i) {if (uf[i] == i) {return i;}uf[i] = find(uf, uf[i]);return uf[i];}
}
示例:
- 提示很重要
- 公共子祖先
- 如果大家是为了面试,不需要了解这个算法
- 如果是为了蓝桥杯,建议看一下这个算法
如果大家有什么思考和问题,可以在评论区讨论,也可以私信我,很乐意为大家效劳。
好啦,今天的每日一题到这里就结束了,如果大家觉得有用,可以可以给我一个小小的赞呢,我们下期再见!
相关文章:

算法每日一题: 边权重均等查询 | 公共子祖先
大家好,我是星恒,今天给大家带来的是一道图里面有关公共子祖先的题目,理解起来简单,大家 题目:leetcode 2846 现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n …...

使用JavaScript和XLSX.js将数据导出为Excel文件
目录 一、安装XLSX.js二、将数据转换为Excel文件 导出数据是Web应用程序中常见的功能之一。在许多情况下,我们需要将数据导出为Excel文件,以便用户可以在本地计算机上查看和编辑数据。在本篇博客中,我们将介绍如何使用JavaScript和XLSX.js将数…...
如何使用YOLOv8训练自己的模型
本文介绍如何用YOLO8训练自己的模型,我们开门见山,直接步入正题。 前言:用yolo8在自己的数据集上训练模型首先需要配置好YOLO8的环境,如果不会配置YOLO8环境可以参考本人主页的另一篇文章 提醒:使用GPU训练会大幅度加…...

机器学习-逻辑回归【手撕】
逻辑回归 在模式识别问题中,所输出的结果是分类,比如是否是猫,这时候无法通过简单的线性回归来实现问题。同时,与线性回归不同的是,逻辑回归是一种名为回归的线性分类器,并常用于二分类,其本质…...

内网安全:NTLM-Relay
目录 NTLM认证过程以及攻击面 NTLM Relay攻击 NTLM攻击总结 实验环境说明 域横向移动:NTLM中继攻击 攻击条件 实战一:NTLM中继攻击-CS转发上线MSF 原理示意图 一. CS代理转发 二. MSF架设路由 三. 适用smb_relay模块进行中继攻击 域横向移动…...

Tensorflow2.0笔记 - tensor的padding和tile
本笔记记录tensor的填充和tile操作,对应tf.pad和tf.tile import tensorflow as tf import numpy as nptf.__version__#pad做填充 # tf.pad( tensor,paddings, modeCONSTANT,nameNone) #1维tensor填充 tensor tf.random.uniform([5], maxval10, dtypetf.int32) pri…...

多媒体测试资源
目录 简介自己整理的文件测试资源列表 简介 音视频测试时,需要许多源文件,这里整理了一些.会持续更新.当然可以使用ffmpeg转换获得需要的文件. 如果知道的这方面资源的,在评论区留言. 自己整理的文件 有视频,图片,音频. 链接:https://pan.baidu.com/s/1vatLmWk…...
Wordpress seo优化该怎么做?
Wordpress作为开源管理系统,目前已然是世界上最流行的cms之一,这不仅仅因为他开源,对用户友好,让任何人都能轻而易举的制作网站,更是因为这套程序对于搜索引擎非常友好,是做谷歌seo的不二之选 Wordpress作为…...
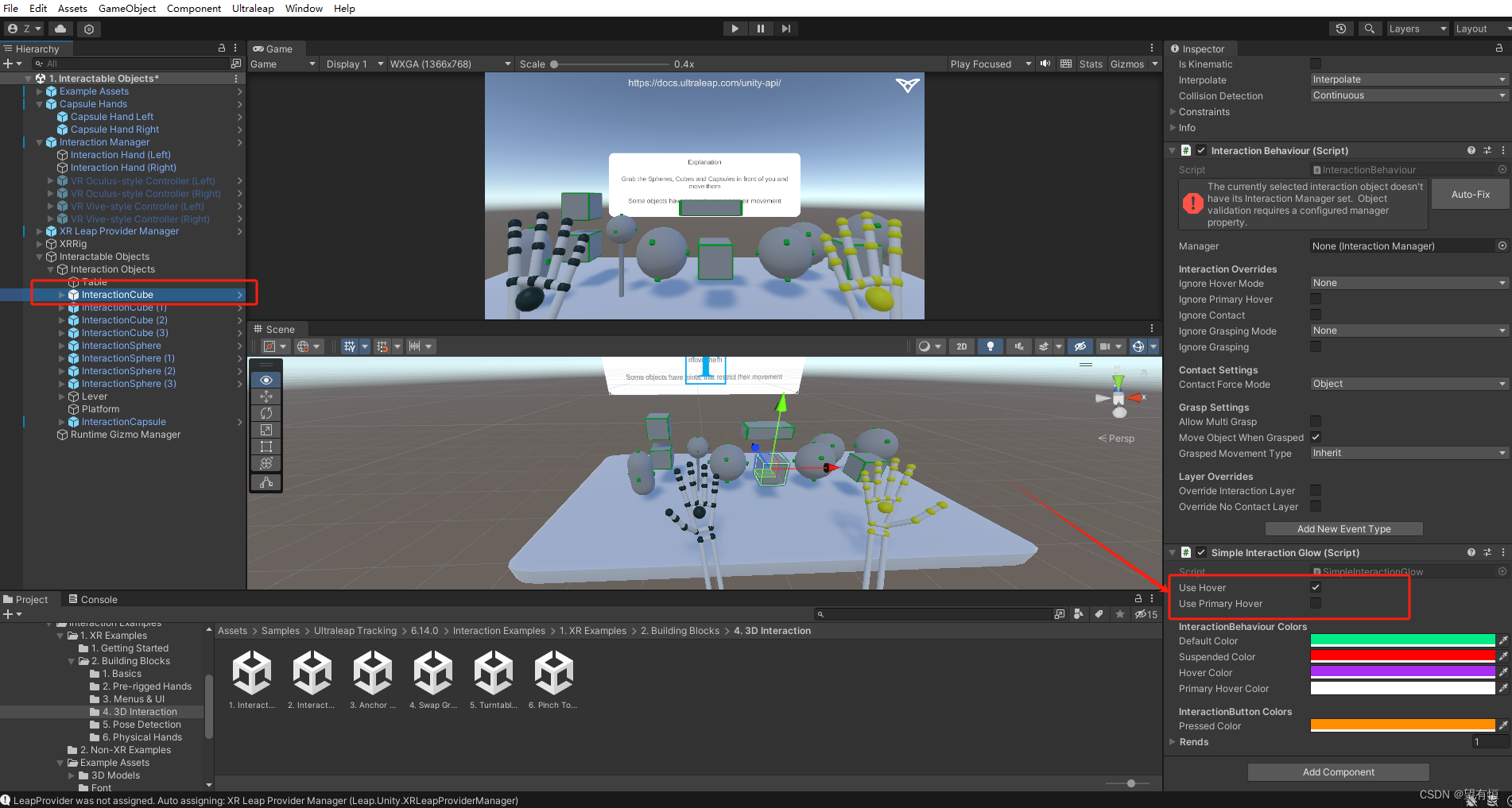
Ultraleap 3Di示例Interactable Objects组件分析
该示例代码位置如下: 分析如下: Hover Enabled:悬停功能,手放在这个模型上,会触发我们手放在这个模型上的悬停功能。此时当手靠近模型的时候,手的模型的颜色会发生改变,反之,则不会…...

Vue自定义成功弹窗H5实现类似于小程序的效果
效果图: <div class"father"><div class"success-box" v-if"isSuccess"><img src"../../assets/insure/success-logo.png" alt""><span>{{ successTitle }}</span></div> &…...

Linux之父:我们正在从C语言转向Rust
最近,Linus在“Torvalds 演讲:人工智能对编程的影响”:“我们正在从C语言转向Rust”。 网友讨论: Linus 选择 Rust 是因为,这是一个中长期解决方案,解决了 IT 世界中缺乏 C/C 人员的实际问题,所…...
C++ qt标题栏组件绘制
本博文源于笔者在学习C qt制作的标题栏组件,主要包含了,最小化,最大化,关闭。读者在看到这篇博文的时候,可以直接查看如何使用的,会使用了,然后进行复制粘贴源码部分即可。 问题来源 想要制作…...

Mysql运维篇(三) MySQL备份与恢复
一路走来,所有遇到的人,帮助过我的、伤害过我的都是朋友,没有一个是敌人。如有侵权,请留言,我及时删除! 一、物理备份与逻辑备份 1、物理备份:备份数据文件,转储数据库物理文件到某…...

数字图像处理(实践篇)二十七 Python-OpenCV 滑动条的使用
目录 1 涉及的函数 2 实践 1 涉及的函数 ⒈ setWindowProperty()用于设置GUI应用程序的属性 cv2.setWindowProperty(windowsName, prop_id, prop_value) 参数: ①...

拷贝构造函数的理解
1.拷贝构造函数与构造函数类似,当没有自定义拷贝构造函数的时候,编译器会定义一个拷贝构造函数。 当类对象没有初始化的时候,通过赋值运算符的形式,也是调用拷贝构造函数。 Test aa(100); Test bb aa;//调用拷贝构造函数Test …...
基于ncurse的floppy_bird小游戏
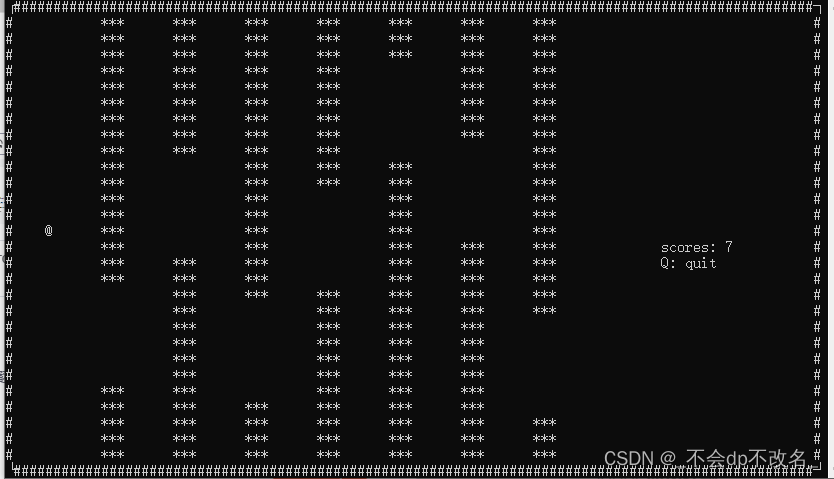
1. 需求分析 将运动分解为鸟的垂直运动和杆的左右运动。 2. 概要设计 2.1 鸟运动部分 2.2 杆的运动 3. 代码实现 #include <stdio.h> #include <ncurses.h>#include <stdlib.h> #include <time.h>int vx 0; int vy 1;int bird_r; int bird_c;int…...
创建第一个 Spring 项目(IDEA社区版)
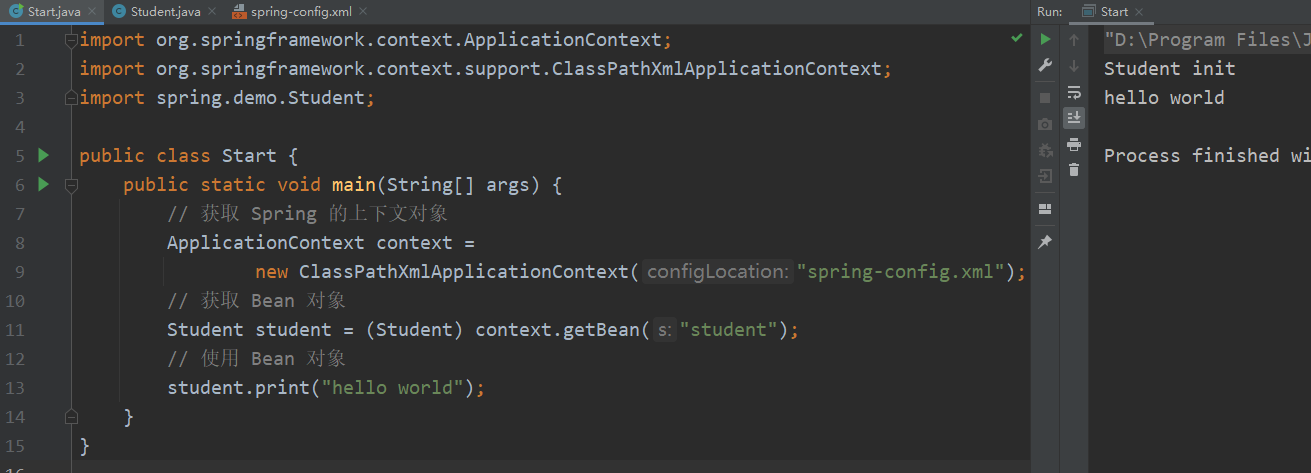
文章目录 创建 Spring 项目创建一个普通的 Maven 项目添加 Spring 依赖IDEA更换国内源 运行第一个 Spring 项目新建启动类存储 Bean 对象将Bean注册到Spring 获取并使用 Bean 对象 创建 Spring 项目 创建一个普通的 Maven 项目 首先创建一个普通的 Maven 项目 添加 Spring 依…...

VUE3动漫影视视频网站模板源码
文章目录 1.视频设计来源1.1 主界面1.2 动漫、电视剧、电影视频界面1.3 播放视频界面1.4 娱乐前线新闻界面1.5 关于我们界面 2.效果和源码2.1 动态效果2.2 源码结构 源码下载 作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_43151418/article/deta…...
Node.js-express
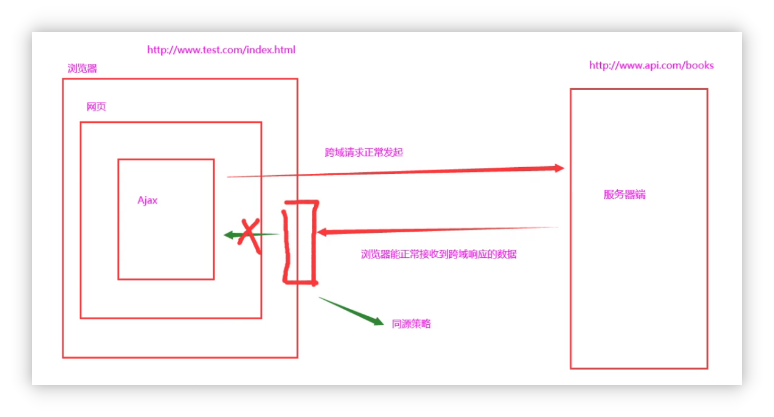
1.了解Ajax 1.1 什么是ajax Ajax的全称是Asynchronous Javascript And XML(异步Js和XML). 通俗的理解:在网页中利用XMLHttpRequest对象和服务器进行数据交互的方式,就是Ajax 1.2 为什么要学习Ajax 之前所学的技术,…...

心理学笔记——我们如何思考-思想、语言和手语
我们如何思考-思想、语言和手语 研究语言的理论:计算理论、认知神经学、进化论 当我们讨论语言时,指的是英语、中文、日语这样的语言系统 所有语言都共享一些深层且复杂的共性,最直观的就是每一种语言都能够有效地表达抽象概念——思想、物…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...
