数据结构奇妙旅程之七大排序
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页:xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
系列专栏:xiaoxie的JAVA系列专栏——CSDN博客●'ᴗ'σσணღ*
我的目标:"团团等我💪( ◡̀_◡́ ҂)"( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注(互三必回)!

一.排序的概念
二.插入排序
1.直接插入排序

1.过程
假设我们有一个数组array{15,87,63,5,98,23,1,82,10} ;我们如果使用直接插入排序的过程如下:
原始: 15 87 63 5 98 23 1 82 10
第一趟: 15 87 63 5 98 23 1 82 10
第二趟: 15 87 63 5 98 23 1 82 10
第三趟:15 63 87 5 98 23 1 82 10
......
第n(9)趟: 1 5 10 15 23 63 82 87 98
2.代码
我们可以把他写为Java代码如下:
public class Sort {public static void insertSort(int[] array) {insert(array,0, array.length-1);}private static void insert(int[] array,int start,int end) {for (int i = start+1; i <= end; i++) {int tmp = array[i];int j = i-1;for (;j >= start; j--) {if(array[j] > tmp) {array[j+1] = array[j];}else {break;}}array[j+1] = tmp;}}
}C++版本如下
#include <iostream>
using namespace std;class Sort {
public:static void insertSort(int array[], int size) {insert(array, 0, size-1);}private:static void insert(int array[], int start, int end) {for (int i = start+1; i <= end; i++) {int tmp = array[i];int j = i-1;for (; j >= start; j--) {if (array[j] > tmp) {array[j+1] = array[j];} else {break;}}array[j+1] = tmp;}}
};3.时间复杂度
最好情况下:
直接插入排序在最好情况下也就是在数据都有序的情况下为O(n)。
最坏情况下:
直接插入排序的最坏情况也就是在数据为逆序的情况下为O(n^2)。
4.空间复杂度
因为直接插入排序是在本数组中实现的没有借用辅助空间所以为O(1)。
5.稳定性
该算法为稳定的
值得注意的是元素集合越接近有序,直接插入排序算法的时间效率越高。
2. 希尔排序( 缩小增量排序 )
1.过程
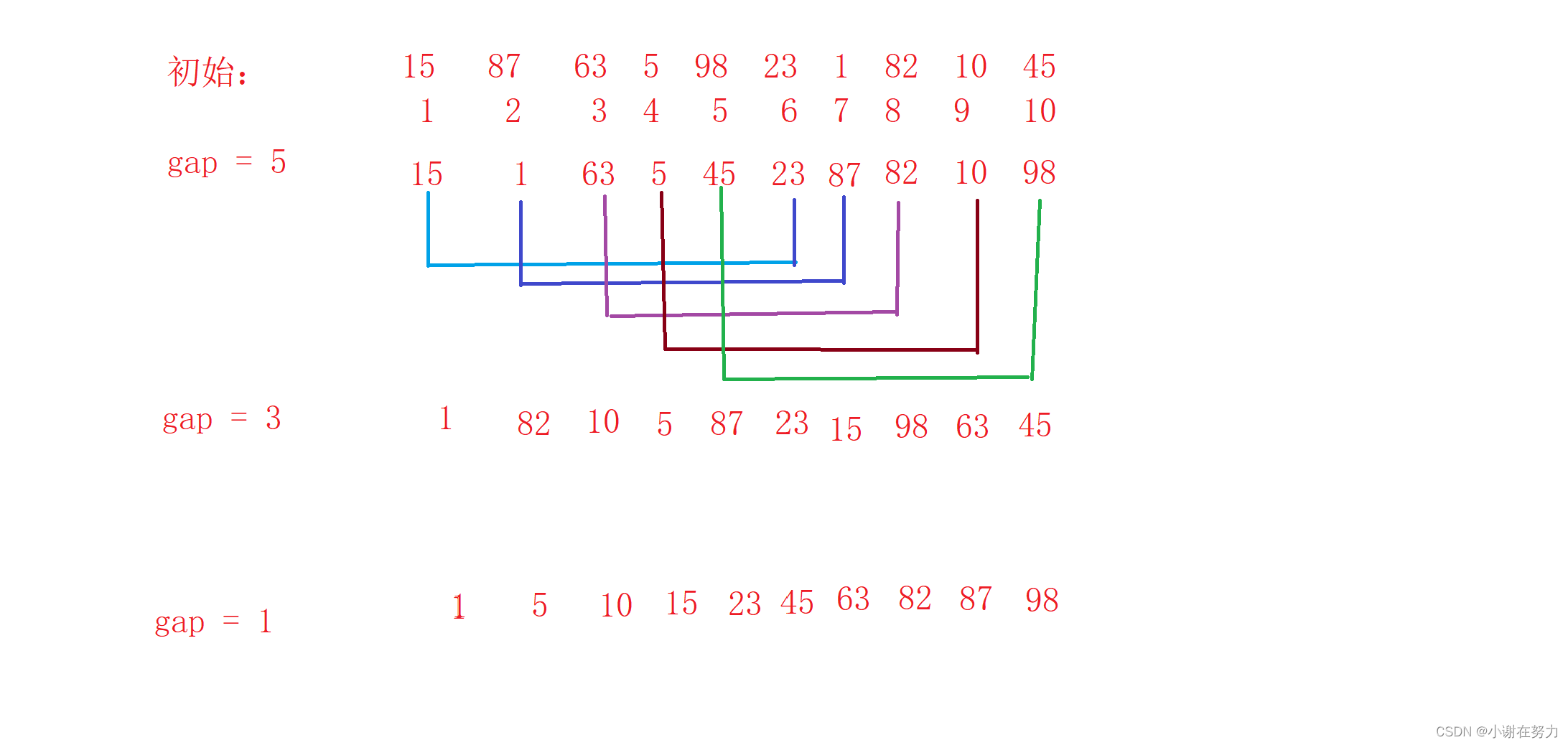
2.代码
java
public class Sort {public static void shellSort(int[] array) {int gap = array.length;while (gap > 1) {gap /= 2;Shell(array,gap);}}private static void Shell(int[] array,int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i-gap;for (; j >= 0; j-=gap) {if(array[j] > tmp) {array[j+gap] = array[j];}else {break;}}array[j+gap] = tmp;}}
}
C++
#include <iostream>
using namespace std;void shellSort(int array[], int size) {int gap = size;while (gap > 1) {gap /= 2;Shell(array, size, gap);}
}void Shell(int array[], int size, int gap) {for (int i = gap; i < size; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j -= gap) {if (array[j] > tmp) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}
}3.时间复杂度

《数据结构-用面向对象方法与C++描述》--- 殷人昆

4.空间复杂度
因为希尔排序是直接插入排序的优化所以是在本数组中实现的没有借用辅助空间所以为O(1)。
5.稳定性
不稳定
6.希尔排序的特性
三.选择排序
3.直接选择排序
1.过程
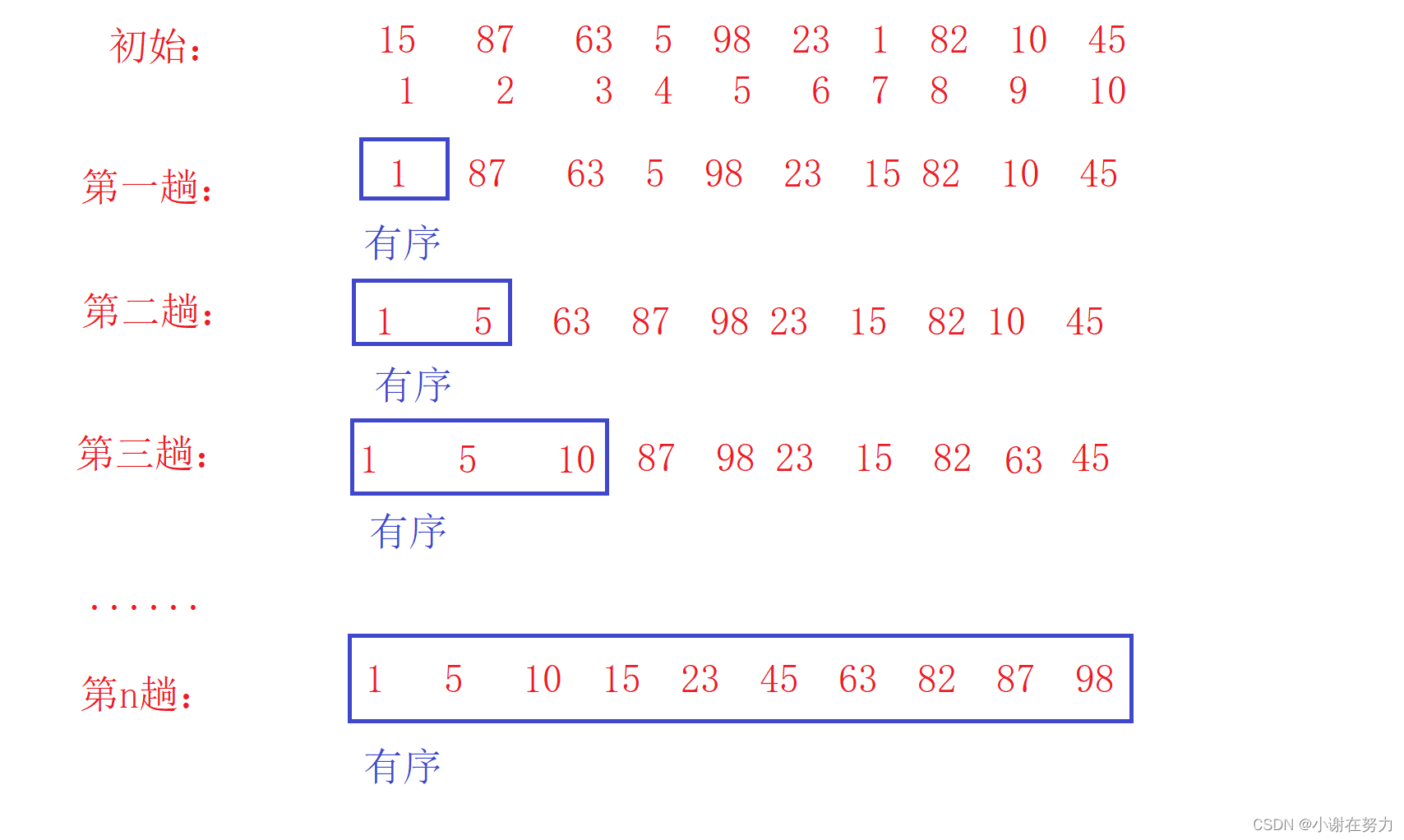
2.代码
Java
public class Sort {public static void selectSort(int[] array) {select(array,0, array.length-1);}private static void select(int[] array,int start,int end) {for (int i = 0; i <= end ; i++) {int minIndex = i;for (int j = i+1; j <= end ; j++) {if(array[j] < array[minIndex]) {minIndex = j;}}swap(array,i,minIndex);}}private static void swap(int[]array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
}#include <iostream>
using namespace std;
void selectSort(int array[], int size) {select(array, 0, size - 1);
}void select(int array[], int start, int end) {for (int i = 0; i <= end; i++) {int minIndex = i;for (int j = i + 1; j <= end; j++) {if (array[j] < array[minIndex]) {minIndex = j;}}swap(array, i, minIndex);}
}void swap(int array[], int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}
3.时间复杂度
最好情况和最坏情况都为:O(n^2) 所以不是很推荐使用
4.空间复杂度
因为直接选择排序是在本数组中实现的没有借用辅助空间所以为O(1)。
5.稳定性
不稳定
4.堆排序(需要重点掌握)
1.过程
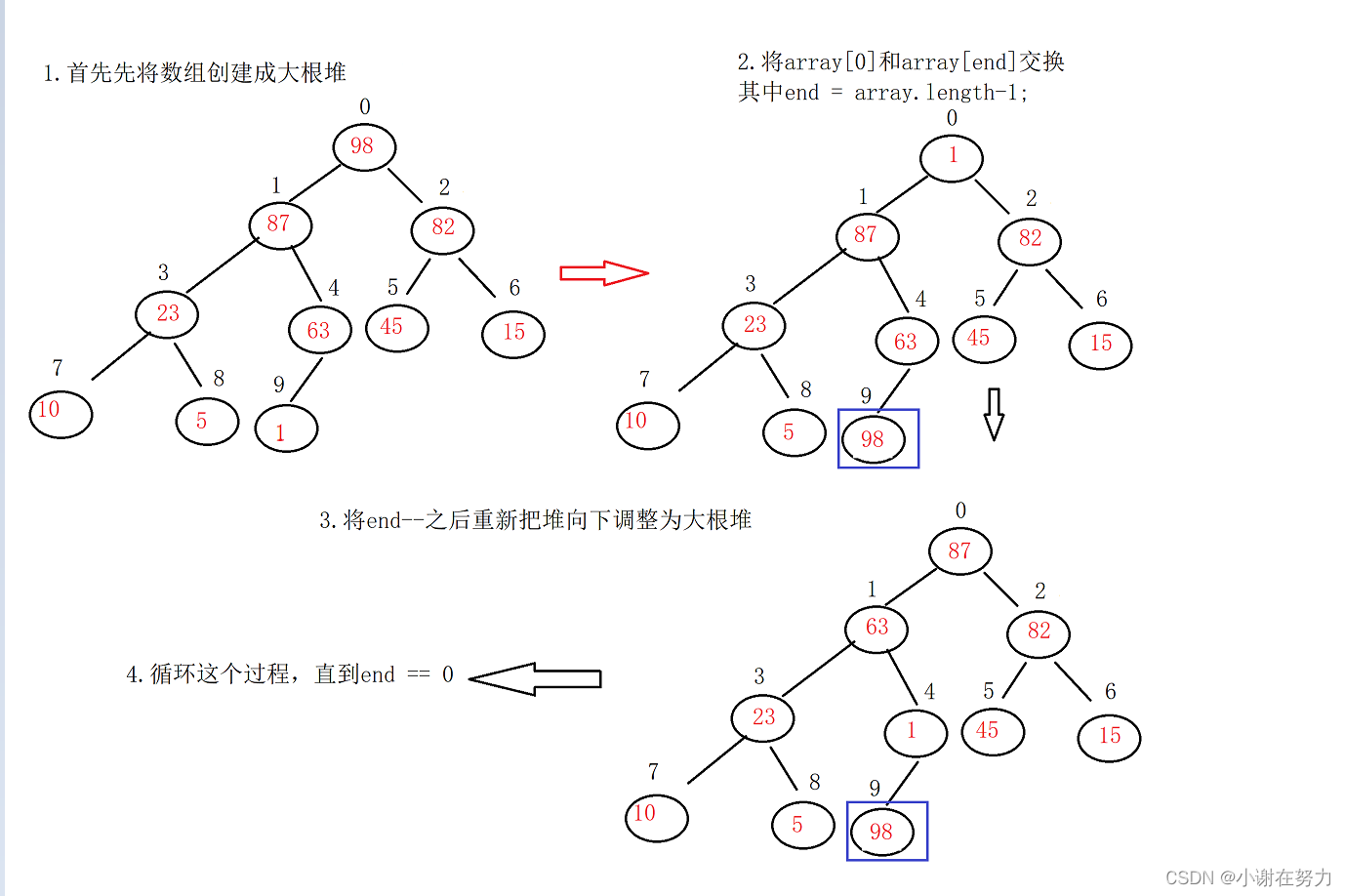
2.代码
Java
private static void swap(int[]array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public static void heapSort(int[] array) {crateHeap(array);//首先创建大根堆int end = array.length-1;while (end >= 0) {swap(array,0,end);siftDown(array,0,end);end--;}}// 创建大根堆private static void crateHeap(int[] array) {for (int parent = (array.length-1-1)/2; parent >= 0; parent--) {siftDown(array,parent,array.length);}}// 向下调整private static void siftDown(int[] array,int parent,int len) {int child = 2*parent+1;while (child < len) {if(child+1 < len && array[child] < array[child+1]) {child++;}if(array[child] > array[parent]) {swap(array,child,parent);parent = child;child = 2*parent+1;}else {break;}}}C++
#include <iostream>
using namespace std;void swap(int array[], int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}void heapSort(int array[], int length) {createHeap(array, length); // 首先创建大根堆int end = length - 1;while (end >= 0) {swap(array, 0, end);siftDown(array, 0, end);end--;}
}// 创建大根堆
void createHeap(int array[], int length) {for (int parent = (length - 2) / 2; parent >= 0; parent--) {siftDown(array, parent, length);}
}// 向下调整
void siftDown(int array[], int parent, int len) {int child = 2 * parent + 1;while (child < len) {if (child + 1 < len && array[child] < array[child + 1]) {child++;}if (array[child] > array[parent]) {swap(array, child, parent);parent = child;child = 2 * parent + 1;} else {break;}}
}
3.时间复杂度
因为堆是一颗完全二叉树所以他的时间复杂度为:O(n*logN)。
4.空间复杂度
没有借助辅助空间所以空间复杂度为:O(1)。
5.稳定性
不稳定
四.交换排序
5.冒泡排序
1.过程
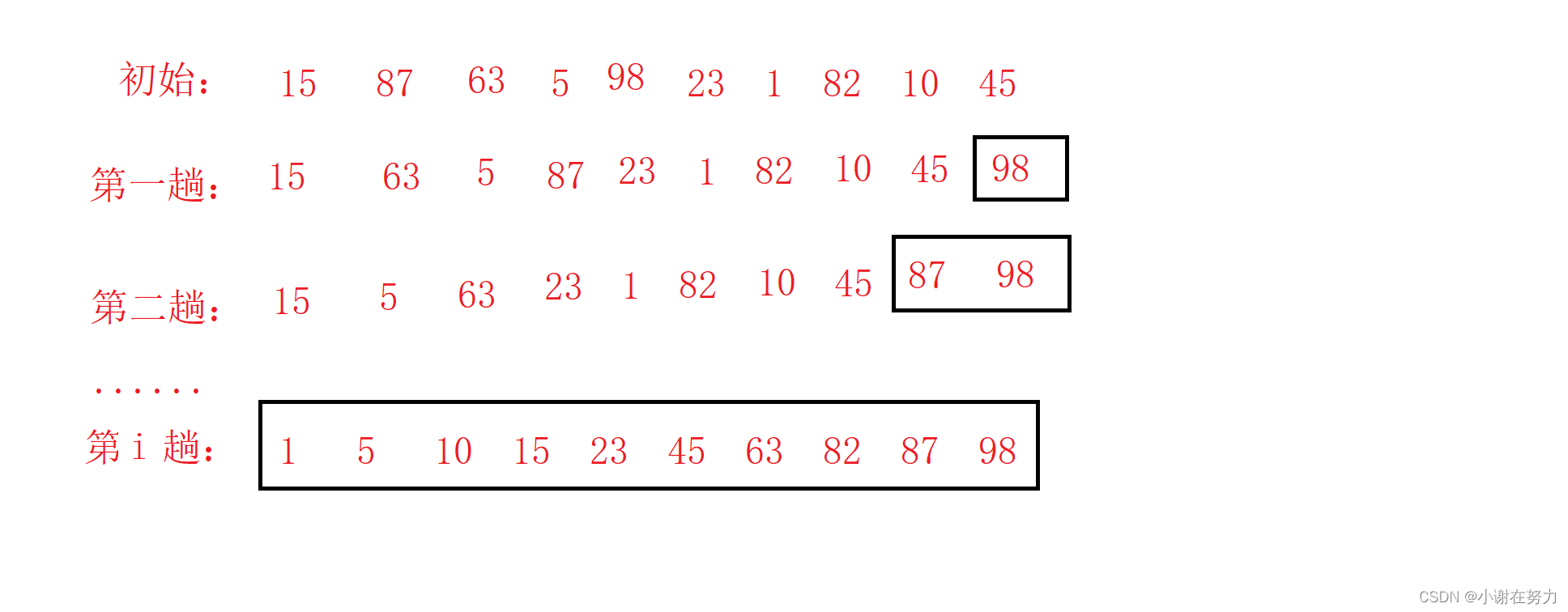
2.代码
Java
private static void swap(int[]array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public static void bubbleSort(int[] array) {//10个元素遍历9趟for (int i = 0; i < array.length-1; i++) {boolean flag = false;for (int j = 0; j < array.length-1-i; j++) {if(array[j] > array[j+1]) {swap(array,j,j+1);flag = true;}}//没有交换就证明有序if(flag == false) {return;}}}C++
#include <iostream>
using namespace std;void swap(int array[], int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}void bubbleSort(int array[], int length) {// 对于10个元素,遍历9趟for (int i = 0; i < length - 1; i++) {bool flag = false;for (int j = 0; j < length - 1 - i; j++) {if (array[j] > array[j + 1]) {swap(array, j, j + 1);flag = true;}}// 若没有交换发生,则证明数组已有序if (!flag) {return;}}
}3.时间复杂度
最好情况下:
冒泡排序在最好情况下也就是在数据都有序的情况下为O(n)。
最坏情况下:
冒泡排序的最坏情况也就是在数据为逆序的情况下为O(n^2)。
4.空间复杂度
没有借助辅助空间所以空间复杂度为:O(1)。
5.稳定性
稳定
6.快速排序(重点掌握)
1.1Hoare法过程
1.2Hoare法代码
private static void swap(int[]array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public static void quickSort(int[] array) {quick(array,0, array.length-1);}private static void quick(int[] array,int left,int right) {if(right-left <= 1) {return;}//三数取中法int index = middleNum(array,left,right);swap(array,left,index);int pivot = partitionHoare(array,left,right);quick(array,left,pivot-1);//递归左边quick(array,pivot+1,right);//递归右边}//三数取中private static int middleNum(int[] array,int start,int end) {int mid = start+((end-start)>>1);if(array[start] < array[end]) {if(array[mid] > array[end]) {return end;} else if (array[mid] < array[start]) {return start;}else {return mid;}}else {if(array[mid] < array[end]) {return end;} else if (array[mid] > array[start]) {return start;}else {return mid;}}}//获取基准值的位置使用Hoare法private static int partitionHoare(int[] array,int left ,int right) {int tmp = array[left];//基准值int i = left;//记录下来基准值开始的下标while (left < right) {while (left < right && array[right] >= tmp) {right--;}while (left < right && array[left] <= tmp) {left++;}swap(array,left,right);}swap(array,left,i);return left;}C++版本
#include <iostream>
using namespace std;void swap(int array[], int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}void quickSort(int array[], int length) {quick(array, 0, length - 1);
}void quick(int array[], int left, int right) {if (right - left <= 1) {return;}// 三数取中法int index = middleNum(array, left, right);swap(array, left, index);int pivot = partitionHoare(array, left, right);quick(array, left, pivot - 1); // 递归左边quick(array, pivot + 1, right); // 递归右边
}// 三数取中
int middleNum(int array[], int start, int end) {int mid = start + ((end - start) >> 1);if (array[start] < array[end]) {if (array[mid] > array[end]) {return end;} else if (array[mid] < array[start]) {return start;} else {return mid;}} else {if (array[mid] < array[end]) {return end;} else if (array[mid] > array[start]) {return start;} else {return mid;}}
}// 获取基准值的位置使用Hoare法
int partitionHoare(int array[], int left, int right) {int tmp = array[left]; // 基准值int i = left; // 记录下来基准值开始的下标while (left < right) {while (left < right && array[right] >= tmp) {right--;}while (left < right && array[left] <= tmp) {left++;}swap(array, left, right);}swap(array, left, i);return left;
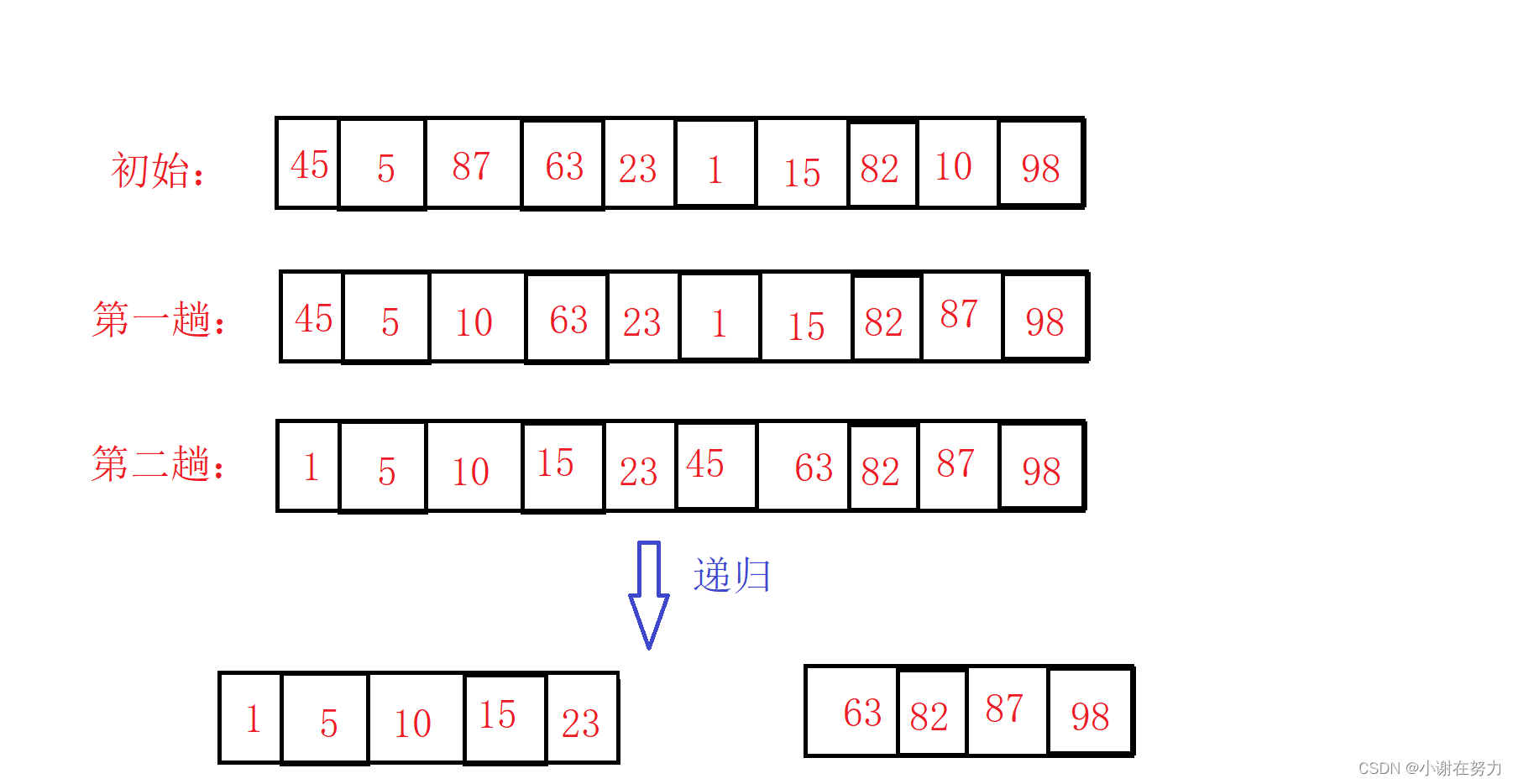
}2.1挖坑法过程(重点掌握)考试选择题过程一般使用挖坑法

2.2 挖坑法代码(重点掌握)
Java
private static void swap(int[]array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public static void quickSort(int[] array) {quick(array,0, array.length-1);}private static void quick(int[] array,int left,int right) {if(right-left <= 1) {return;}//三数取中法int index = middleNum(array,left,right);swap(array,left,index);int pivot = partition(array,left,right);quick(array,left,pivot-1);//递归左边quick(array,pivot+1,right);//递归右边}//三数取中private static int middleNum(int[] array,int start,int end) {int mid = start+((end-start)>>1);if(array[start] < array[end]) {if(array[mid] > array[end]) {return end;} else if (array[mid] < array[start]) {return start;}else {return mid;}}else {if(array[mid] < array[end]) {return end;} else if (array[mid] > array[start]) {return start;}else {return mid;}}}//获取基准值的位置使用挖坑法private static int partition(int[] array,int left ,int right) {int tmp = array[left];//记录基准值while (left < right) {while (left < right && array[right] >= tmp) {right--;}array[left] = array[right];while (left < right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;// 将基准值放入正确位置return left;}C++
#include <iostream>
using namespace std;void swap(int array[], int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}void quickSort(int array[], int length) {quick(array, 0, length - 1);
}void quick(int array[], int left, int right) {if (right - left <= 1) {return;}// 三数取中法int index = middleNum(array, left, right);swap(array, left, index);int pivot = partition(array, left, right);quick(array, left, pivot - 1); // 递归左边quick(array, pivot + 1, right); // 递归右边
}// 三数取中
int middleNum(int array[], int start, int end) {int mid = start + ((end - start) >> 1);if (array[start] < array[end]) {if (array[mid] > array[end]) {return end;} else if (array[mid] < array[start]) {return start;} else {return mid;}} else {if (array[mid] < array[end]) {return end;} else if (array[mid] > array[start]) {return start;} else {return mid;}}
}// 获取基准值的位置使用挖坑法
int partition(int array[], int left, int right) {int pivot = array[left]; // 基准值while (left < right) {while (left < right && array[right] >= pivot) {right--;}array[left] = array[right];while (left < right && array[left] <= pivot) {left++;}array[right] = array[left];}array[left] = pivot; // 将基准值放入正确位置return left;
}3.时间复杂度
最好情况下数据为无序的时候为O(n*logN)。
最坏情况下数据为有序或者是逆序的时候为O(n^2)。
4.空间复杂度
在递归调用过程中,需要使用O(log n)的栈空间来存储递归调用的上下文信息所以空间复杂度为:O(logN)。
5.稳定性
不稳定
7.归并排序(重点掌握)
1.过程
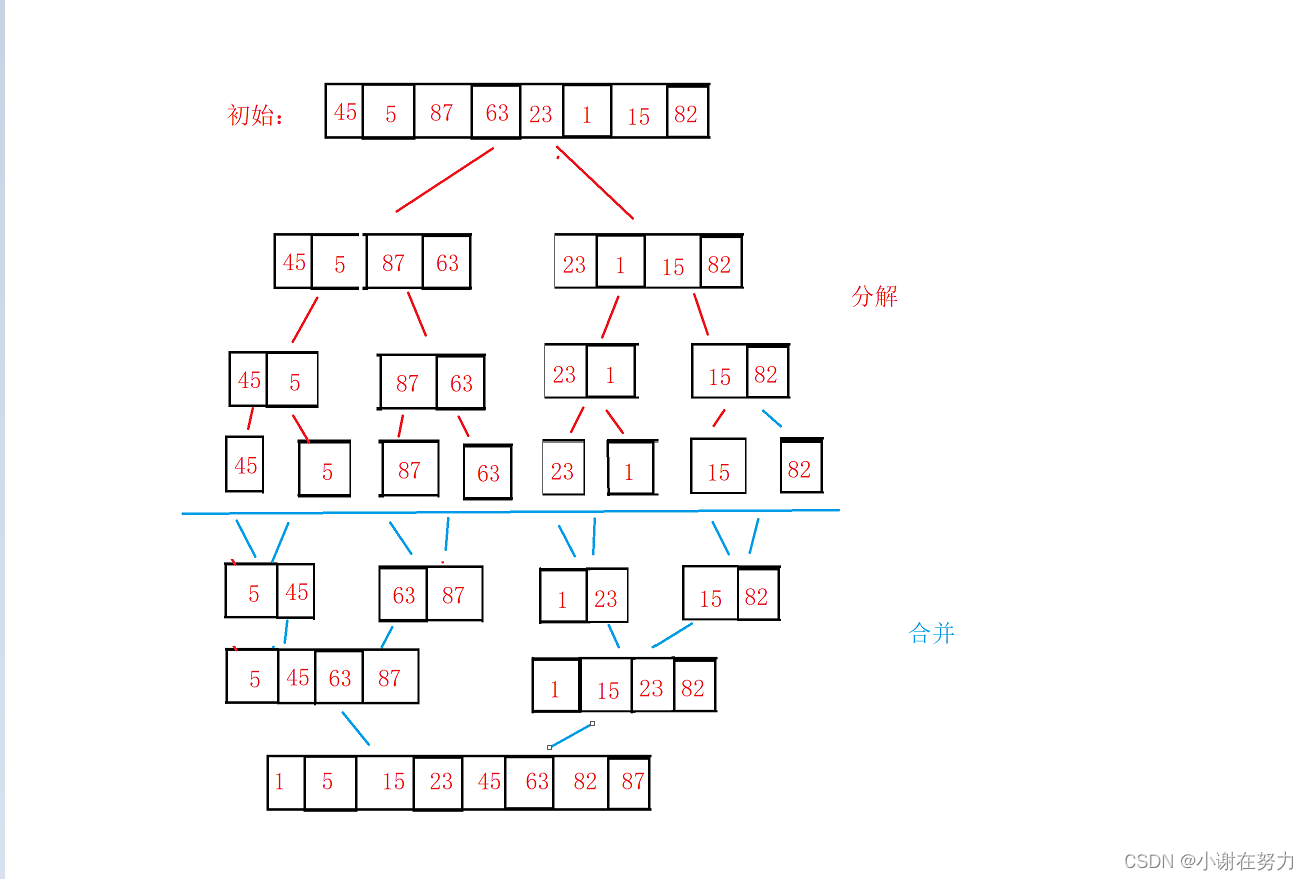
2.代码
Java
public static void mergeSort(int[] array) {mergeFunc(array,0,array.length-1);}private static void mergeFunc(int[] array,int left,int right) {if(left >= right) {return;}int mid = left + ((right-left) >> 1);//开始分解mergeFunc(array,left,mid);mergeFunc(array, mid+1, right);//开始合并merge(array,left,right,mid);}private static void merge(int[] array,int left,int right,int mid) {int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;int[] tmp = new int[right-left+1];//创建一个临时数组来储存数据int k = 0;//临时数组下标while (s1 <= e1 && s2 <= e2) {if(array[s1] <= array[s2]) {tmp[k++] = array[s1++];}else {tmp[k++] = array[s2++];}}//看那个数组还有数据就拷贝过去while (s1 <= e1) {tmp[k++] = array[s1++];}while (s2 <= e2) {tmp[k++] = array[s2++];}//3.拷贝到源数组for (int i = 0; i < k; i++) {array[i+left] = tmp[i];}}C++
#include <iostream>
using namespace std;void mergeSort(int array[], int length) {mergeFunc(array, 0, length - 1);
}void mergeFunc(int array[], int left, int right) {if (left >= right) {return;}int mid = left + ((right - left) >> 1);// 开始分解mergeFunc(array, left, mid);mergeFunc(array, mid + 1, right);// 开始合并merge(array, left, right, mid);
}void merge(int array[], int left, int right, int mid) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int tmp[right - left + 1]; // 创建一个临时数组来储存数据int k = 0; // 临时数组下标while (s1 <= e1 && s2 <= e2) {if (array[s1] <= array[s2]) {tmp[k++] = array[s1++];} else {tmp[k++] = array[s2++];}}// 看那个数组还有数据就拷贝过去while (s1 <= e1) {tmp[k++] = array[s1++];}while (s2 <= e2) {tmp[k++] = array[s2++];}// 3.拷贝到源数组for (int i = 0; i < k; i++) {array[i + left] = tmp[i];}
}3.时间复杂度
时间复杂度为O(n*logN)。
4.空间复杂度
因为需要借助临时数组所以空间复杂度为O(n)。
5.稳定性
稳定
五.各个排序算法的时间复杂度和空间复杂度以及稳定性总结

以上就是关于基于比较排序的所以的内容了,如果有帮助到你,创作不易希望可以给博主一个关注,感谢你的阅读,希望能够对你有所帮助
相关文章:

数据结构奇妙旅程之七大排序
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN …...

【JavaScript】Generator
MDN-Generator Generator对象由生成器函数返回,并且它符合可迭代协议和迭代器协议。 Generator-核心语法 核心语法: 定义生成器函数获取generator对象yield表达式的使用通过for of获取每一个yield的值 // 1. 通过function* 创建生成器函数 function* foo() {//…...

河南省考后天网上确认,请提前准备证件照哦
✔报名时间:2024年1月18号一1月24号 ✔报名确认和缴费:2024年1月 31号一2月4号 ✔准考证打印:2024年3月12号一3月17号 ✔笔试时间:2024年3月16日-2024年3月17日。 ✔面试时间:面试时间拟安排在2024年5月中旬 报名网址&…...

【前端】防抖和节流
防抖 防抖用于限制连续触发的事件的执行频率。当一个事件被触发时,防抖会延迟一定的时间执行对应的处理函数。如果在延迟时间内再次触发了同样的事件,那么之前的延迟执行将被取消,重新开始计时。 总结:在单位时间内频繁触发事件,只有最后一次生效 场景 :用户在输入框输…...

【网络】:网络套接字(UDP)
网络套接字 一.网络字节序二.端口号三.socket1.常见的API2.封装UdpSocket 四.地址转换函数 网络通信的本质就是进程间通信。 一.网络字节序 我们已经知道,内存中的多字节数据相对于内存地址有大端和小端之分, 磁盘文件中的多字节数据相对于文件中的偏移地址也有大端小端之分,网…...

Linux编程 1/2 数据结构
数据结构: 程序 数据结构 算法 1.数据结构: 1.时间复杂度: 数据量的增长与程序运行时间增长所呈现的比例函数,则称为时间渐进复杂度函数简称时间复杂度 O(c) > O(logn)> O(n) > O(nlogn) > O(n^2) > O(n^3) > O(2^n) 2.空间复杂度: 2.类…...

【UE Niagara】实现闪电粒子效果的两种方式
目录 效果 步骤 方式一(网格体渲染器) (1)添加网格体渲染器 (2)修改粒子显示方向 (3)添加从上到下逐渐显现的效果 (4)粒子颜色变化 方式二࿰…...
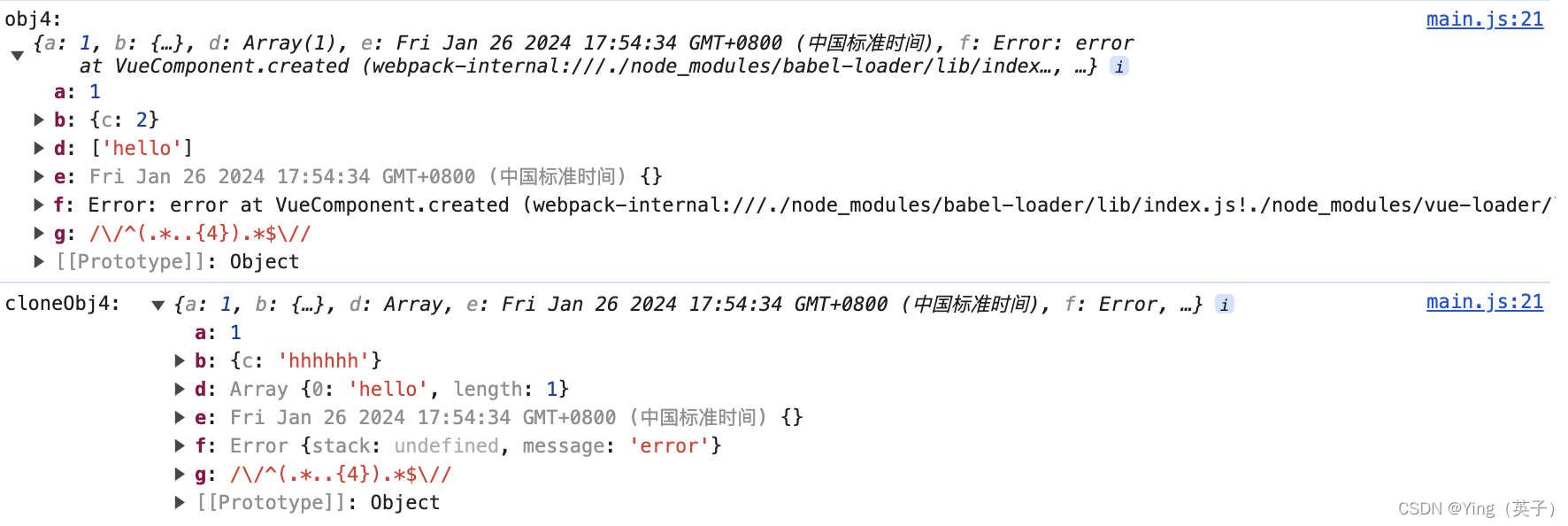
js数组/对象的深拷贝与浅拷贝
文章目录 一、js中的深拷贝和浅拷贝二、浅拷贝1、Object.assign()2、利用es6扩展运算符(...) 二、深拷贝1、JSON 序列化和反序列化2、js原生代码实现3、使用第三方库lodash等 四、总结 一、js中的深拷贝和浅拷贝 在JS中,深拷贝和浅拷贝是针对…...
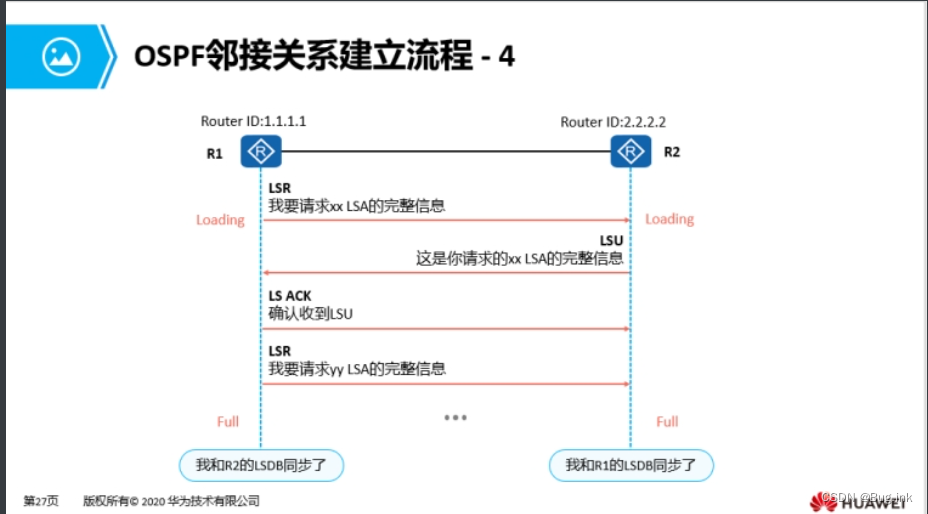
HCIA学习第六天:OSPF:开放式最短路径优先协议
OSPF:开放式最短路径优先协议 无类别链路状态IGP动态路由协议 1.距离矢量协议:运行距离矢量协议的路由器会周期性的泛洪自己的路由表。通过路由的交互,每台路由器从相邻的路由器学习到路由,并且加载进自己的路由表中;…...
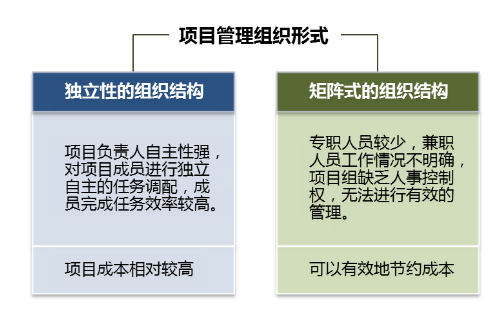
从四个方面来解决企业在项目管理中遇到的各类问题
案例背景:某建筑集团有限公司成立于1949年,拥有国家房屋建筑工程施工总承包一级、建筑装修装饰工程专业承包一级、市政公用工程施工总承包一级资质。是一家集建筑施工、设备安装、装饰装潢、仿古建筑、房地产开发、建材试验为一体的具有综合生产能力的建…...
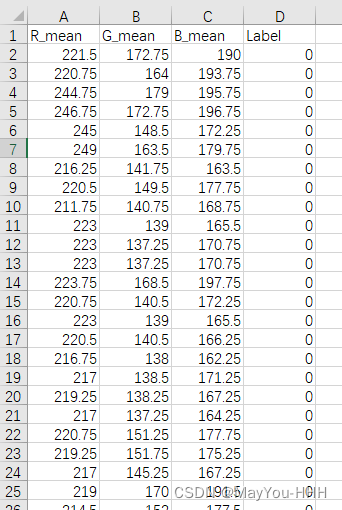
使用代码取大量2*2像素图片各通道均值,存于Excel文件中。
任务是取下图RGB各个通道的均值及标签(R, G,B,Label),其中标签由图片存放的文件夹标识。由于2*2像素图片较多,所以将结果放置于Excel表格中,之后使用SVM对他们进行分类。 from PIL import Image import os …...

React16源码: React中commit阶段的commitBeforeMutationLifecycles的源码实现
commitBeforeMutationLifecycles 1 )概述 在 react commit 阶段的 commitRoot 第一个while循环中调用了 commitBeforeMutationLifeCycles现在来看下,里面发生了什么 2 )源码 回到 commit 阶段的第一个循环中,在 commitRoot 函数…...

压制二元组的总价值
压制二元组的总价值 对于每一个 a i a_i ai, 看它能压制它前面的多少个元素, 那么它对总价值的贡献就是: 在a数组中: a i a_i ai压制了x个数, 贡献为: x ∗ i x*i x∗i被 a i a_i ai所压制的所有数在 a a a中的下标和为 y y y, 贡献为 − y -y −y 树状数组来求: 为了…...

【习题】保存应用数据
判断题 1. 首选项是关系型数据库。 错误(False) 2. 应用中涉及到Student信息,如包含姓名,性别,年龄,身高等信息可以用首选项来存储。 错误(False) 3. 同一应用或进程中每个文件仅存在一个Preferences实例。 正确(True) 单选题 …...
Flask框架小程序后端分离开发学习笔记《5》简易服务器代码
Flask框架小程序后端分离开发学习笔记《5》 Flask是使用python的后端,由于小程序需要后端开发,遂学习一下后端开发。 简易服务器代码 接口解析那一块很关键,学后端服务器这一块,感觉主要就是学习相应地址的接口怎么处理。 然后…...

“计算机视觉处理设计开发工程师”专项培训(第二期)
“人工智能技术与咨询” 发布...
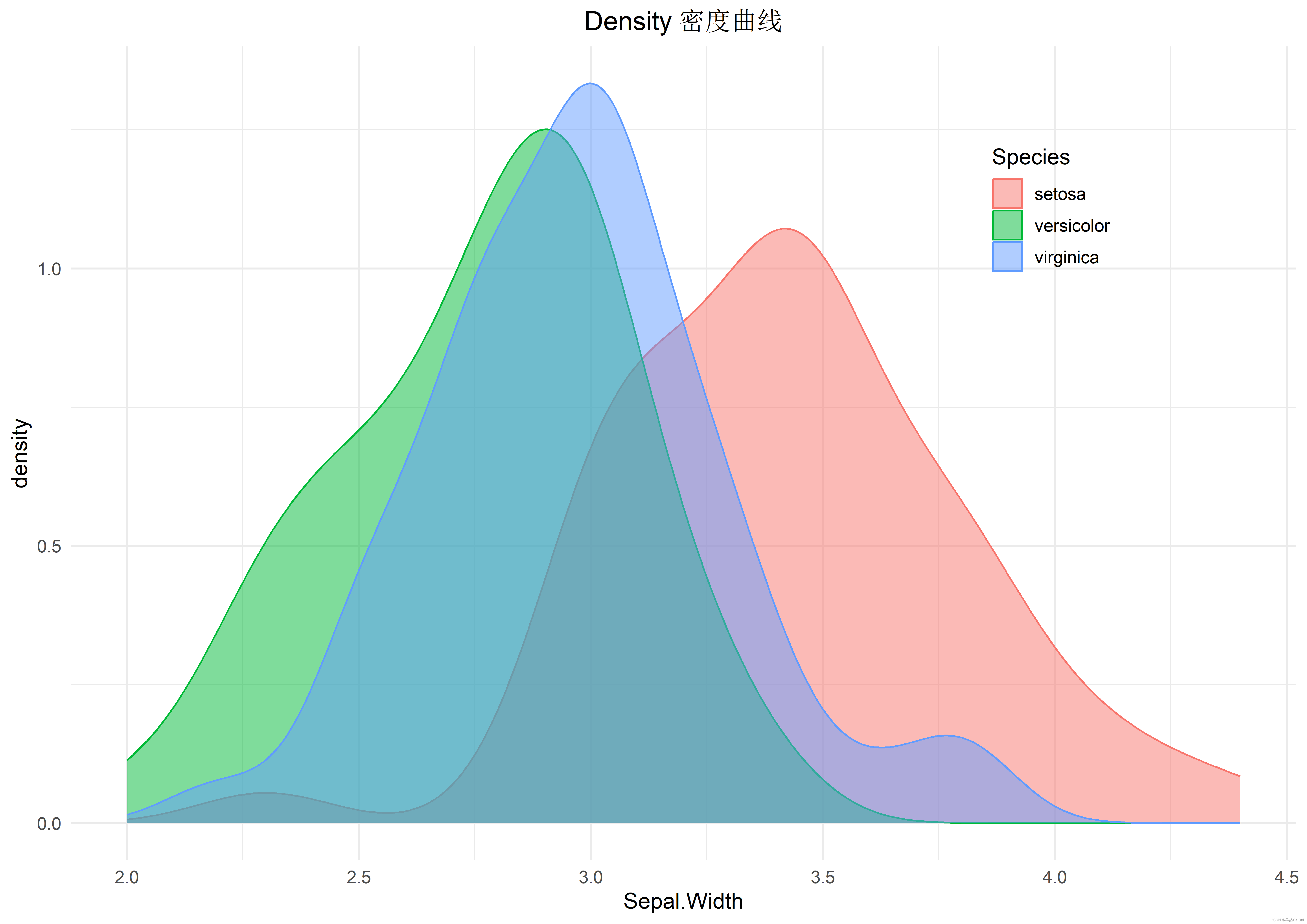
R语言学习case7:ggplot基础画图(核密度图)
step1: 导入ggplot2库文件 library(ggplot2)step2:带入自带的iris数据集 iris <- datasets::irisstep3:查看数据信息 dim(iris)维度为 [150,5] head(iris)查看数据前6行的信息 step4:画图展示 plot2 <- ggplot(iris,aes(Sepal.W…...

Ubuntu18配置Docker
1.基本过程 1.更新软件源列表 sudo apt update2.安装软件包依赖 sudo apt install apt-transport-https ca-certificates curl software-properties-common3.在系统中添加Docker的官方密钥 curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add - …...

Keil/MDK平台 - 结构体成员指针注意事项
文章目录 1 . 前言总结2 . 问题现象3 . 解决思路4 . 细节扩展5 . 总结 【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485 1 . 前言总结 有时候希望通过类定义的类型指向数据包来解析,恰好又想结构体内定义指针指向一段数据&…...
一款超级好用的远程控制APP,你值得拥有
在这个科技日新月异的时代,我们的生活被各种手机软件所包围。几乎每个人都有一个甚至多个手机,你是否也有遇到过需要远程操作自己某一台手机的场景呢?今天,我要向大家推荐一款神奇的手机远程操作神器,让你可以随时随地…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
