Linux编程 1/2 数据结构
数据结构:
程序 = 数据结构 + 算法
1.数据结构:
1.时间复杂度:
数据量的增长与程序运行时间增长所呈现的比例函数,则称为时间渐进复杂度函数简称时间复杂度
O(c) > O(logn)> O(n) > O(nlogn) > O(n^2) > O(n^3) > O(2^n)
2.空间复杂度:
2.类型:
1.逻辑结构
线性结构(一对一)
表
非线性结构(一对多、多对多)
树
图
2.存储结构
顺序存储
链式存储
散列存储
索引存储
3.数据结构:
顺序表
链式表(重点)
单向链表
双向链表
循环链表
内核链表
顺序栈
链式栈
顺序队列
链式队列
二叉树
排序查找算法
4.顺序表:
对数据增删改查
5.链式表:
链式存储的表状结构,链表可以分为:单向链表、双向链表、循环链表、内核链表
优点:
1.只要空间足够,理论上可以存放无限个数据
2.链表插入和删除效率高
缺点:
1.数据访问不太方便(空间不连续)
2.会使结构所占存储空间变大
相关文章:

Linux编程 1/2 数据结构
数据结构: 程序 数据结构 算法 1.数据结构: 1.时间复杂度: 数据量的增长与程序运行时间增长所呈现的比例函数,则称为时间渐进复杂度函数简称时间复杂度 O(c) > O(logn)> O(n) > O(nlogn) > O(n^2) > O(n^3) > O(2^n) 2.空间复杂度: 2.类…...

【UE Niagara】实现闪电粒子效果的两种方式
目录 效果 步骤 方式一(网格体渲染器) (1)添加网格体渲染器 (2)修改粒子显示方向 (3)添加从上到下逐渐显现的效果 (4)粒子颜色变化 方式二࿰…...
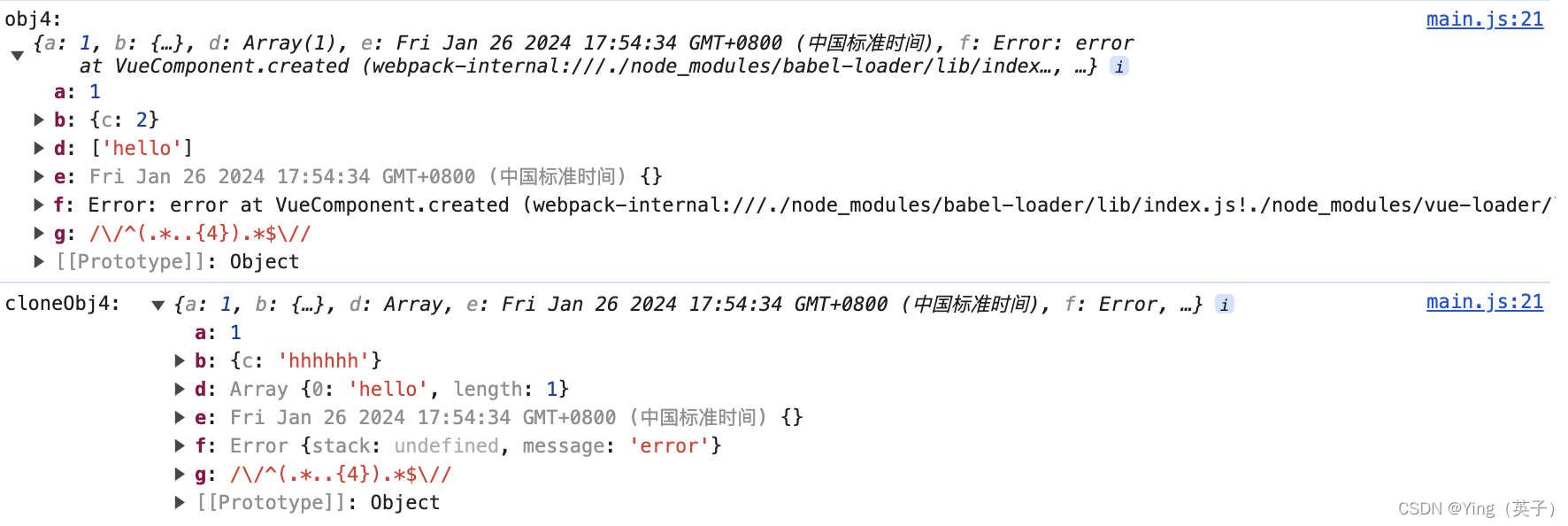
js数组/对象的深拷贝与浅拷贝
文章目录 一、js中的深拷贝和浅拷贝二、浅拷贝1、Object.assign()2、利用es6扩展运算符(...) 二、深拷贝1、JSON 序列化和反序列化2、js原生代码实现3、使用第三方库lodash等 四、总结 一、js中的深拷贝和浅拷贝 在JS中,深拷贝和浅拷贝是针对…...
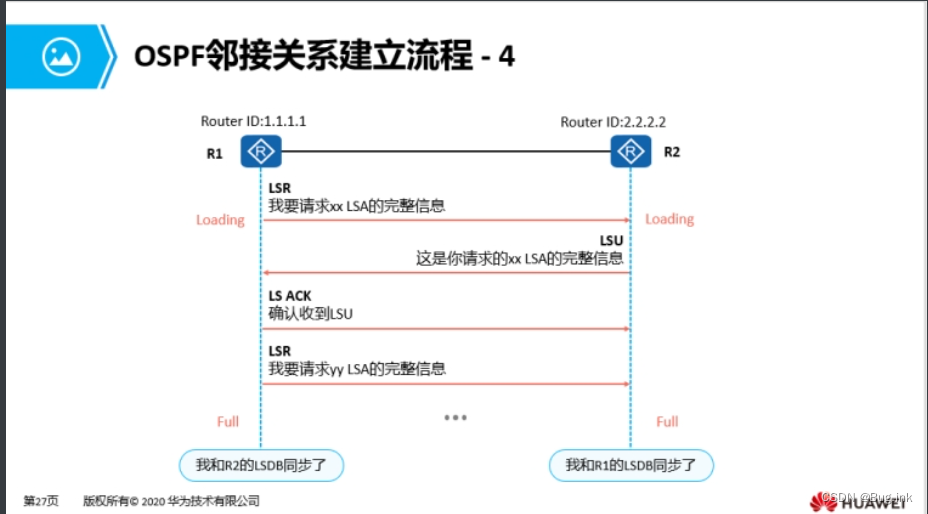
HCIA学习第六天:OSPF:开放式最短路径优先协议
OSPF:开放式最短路径优先协议 无类别链路状态IGP动态路由协议 1.距离矢量协议:运行距离矢量协议的路由器会周期性的泛洪自己的路由表。通过路由的交互,每台路由器从相邻的路由器学习到路由,并且加载进自己的路由表中;…...
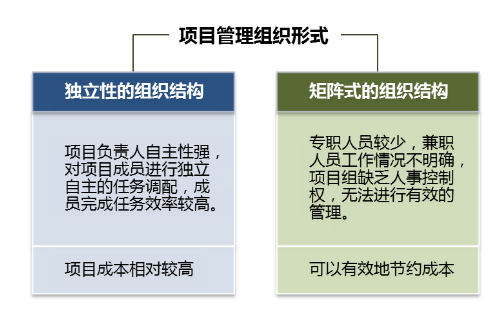
从四个方面来解决企业在项目管理中遇到的各类问题
案例背景:某建筑集团有限公司成立于1949年,拥有国家房屋建筑工程施工总承包一级、建筑装修装饰工程专业承包一级、市政公用工程施工总承包一级资质。是一家集建筑施工、设备安装、装饰装潢、仿古建筑、房地产开发、建材试验为一体的具有综合生产能力的建…...
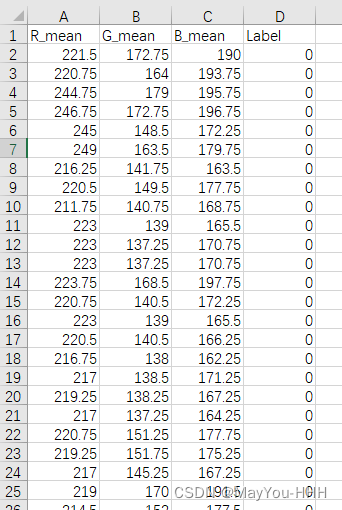
使用代码取大量2*2像素图片各通道均值,存于Excel文件中。
任务是取下图RGB各个通道的均值及标签(R, G,B,Label),其中标签由图片存放的文件夹标识。由于2*2像素图片较多,所以将结果放置于Excel表格中,之后使用SVM对他们进行分类。 from PIL import Image import os …...

React16源码: React中commit阶段的commitBeforeMutationLifecycles的源码实现
commitBeforeMutationLifecycles 1 )概述 在 react commit 阶段的 commitRoot 第一个while循环中调用了 commitBeforeMutationLifeCycles现在来看下,里面发生了什么 2 )源码 回到 commit 阶段的第一个循环中,在 commitRoot 函数…...

压制二元组的总价值
压制二元组的总价值 对于每一个 a i a_i ai, 看它能压制它前面的多少个元素, 那么它对总价值的贡献就是: 在a数组中: a i a_i ai压制了x个数, 贡献为: x ∗ i x*i x∗i被 a i a_i ai所压制的所有数在 a a a中的下标和为 y y y, 贡献为 − y -y −y 树状数组来求: 为了…...

【习题】保存应用数据
判断题 1. 首选项是关系型数据库。 错误(False) 2. 应用中涉及到Student信息,如包含姓名,性别,年龄,身高等信息可以用首选项来存储。 错误(False) 3. 同一应用或进程中每个文件仅存在一个Preferences实例。 正确(True) 单选题 …...
Flask框架小程序后端分离开发学习笔记《5》简易服务器代码
Flask框架小程序后端分离开发学习笔记《5》 Flask是使用python的后端,由于小程序需要后端开发,遂学习一下后端开发。 简易服务器代码 接口解析那一块很关键,学后端服务器这一块,感觉主要就是学习相应地址的接口怎么处理。 然后…...

“计算机视觉处理设计开发工程师”专项培训(第二期)
“人工智能技术与咨询” 发布...
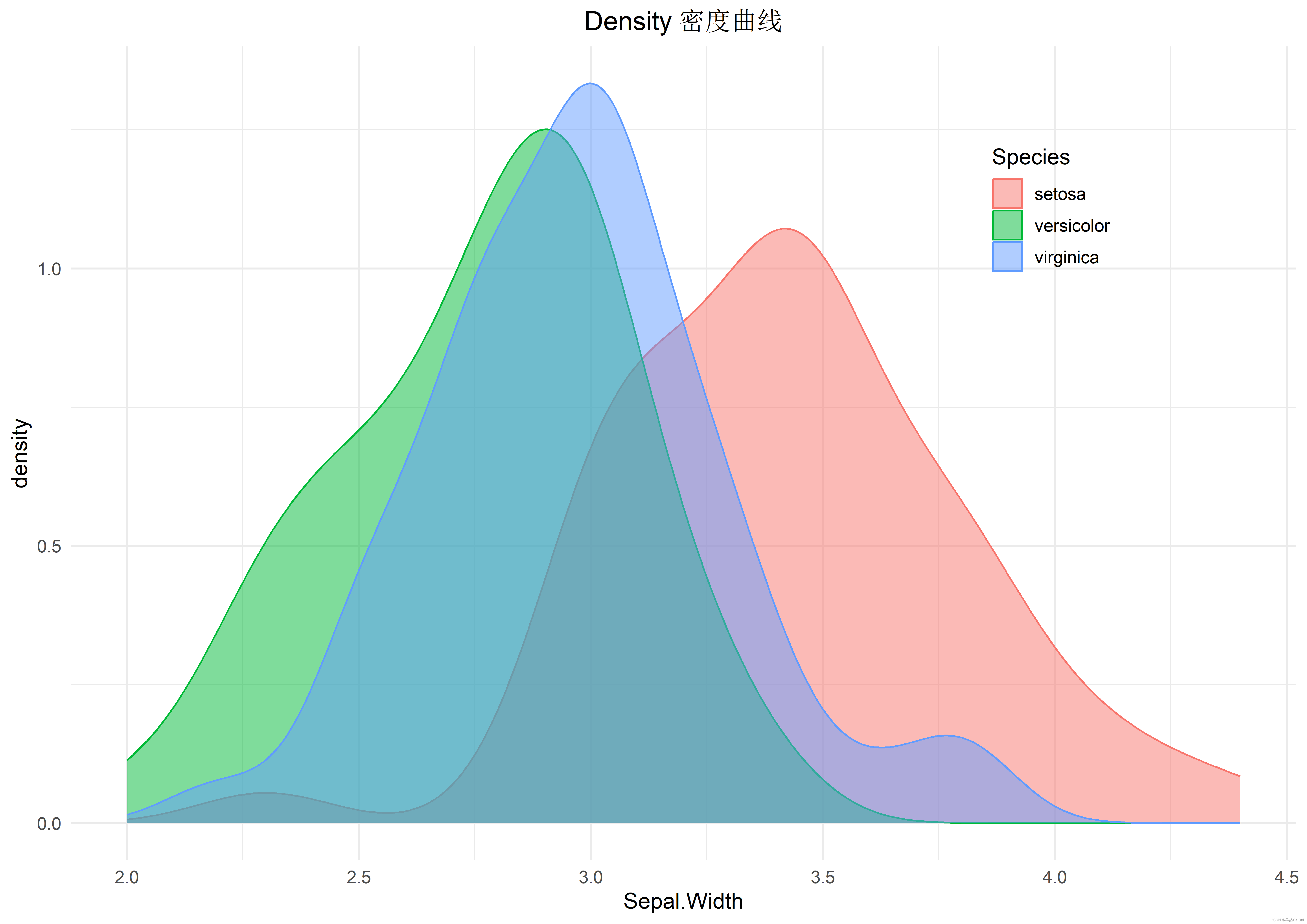
R语言学习case7:ggplot基础画图(核密度图)
step1: 导入ggplot2库文件 library(ggplot2)step2:带入自带的iris数据集 iris <- datasets::irisstep3:查看数据信息 dim(iris)维度为 [150,5] head(iris)查看数据前6行的信息 step4:画图展示 plot2 <- ggplot(iris,aes(Sepal.W…...

Ubuntu18配置Docker
1.基本过程 1.更新软件源列表 sudo apt update2.安装软件包依赖 sudo apt install apt-transport-https ca-certificates curl software-properties-common3.在系统中添加Docker的官方密钥 curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add - …...

Keil/MDK平台 - 结构体成员指针注意事项
文章目录 1 . 前言总结2 . 问题现象3 . 解决思路4 . 细节扩展5 . 总结 【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485 1 . 前言总结 有时候希望通过类定义的类型指向数据包来解析,恰好又想结构体内定义指针指向一段数据&…...
一款超级好用的远程控制APP,你值得拥有
在这个科技日新月异的时代,我们的生活被各种手机软件所包围。几乎每个人都有一个甚至多个手机,你是否也有遇到过需要远程操作自己某一台手机的场景呢?今天,我要向大家推荐一款神奇的手机远程操作神器,让你可以随时随地…...

NumPy必知必会50例 | 18. 使用 NumPy 解决线性方程组:数学问题的实用解决方案
继续我们的 NumPy 探索之旅吧,接下来我们将探讨使用 NumPy 解决线性方程组,一种实用的数学应用。 文章目录 18. 使用 NumPy 解决线性方程组:数学问题的实用解决方案线性方程组:数学世界的基石创建线性方程组 解决实际问题应用场景…...
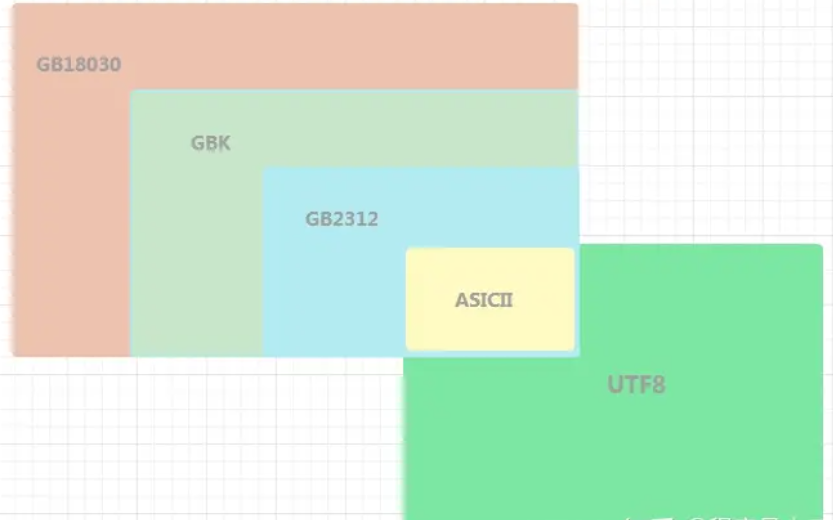
C/C++编码问题研究
文章目录 一、Unicode字符集与U8/U16/U32编码二、编码1. 占字节数2. ASCII、GB2312、GBK、GB18030 以及 UTF8 的关系3. BOM4. UTF-8的存储实现 三、编译器字符集设置1. GCC语法Example 2. MSVC语法Example 三、wchar_t五、编码转换函数六、代码 & 实践1. UTF8与UTF16、UTF3…...

二刷代码随想录|Java版|回溯算法3|子集问题
习题 2.3 子集问题 就是组合过程收集path。就像是代码随想录里说得那样,组合和分割问题就是收集叶子结点,子集问题就是收集每一个节点。 有涉及到同层重复元素的问题。 先排序,后再for循环里处理相同数值跳过。 设置函数内的used。 还可以用…...

mongodb config
windows: 1.同级bin,data,log创建mongo.config文件 dbpathD:\Program\mongodb\data\db logpathD:\Program\mongodb\log\mongo.log logappendtrue #默认启用日志 journaltrue #过滤无用日志信息,调试设置为false quiettrue port2…...

pytorch 实现中文文本分类
🍨 本文为[🔗365天深度学习训练营学习记录博客🍦 参考文章:365天深度学习训练营🍖 原作者:[K同学啊 | 接辅导、项目定制]\n🚀 文章来源:[K同学的学习圈子](https://www.yuque.com/mi…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
