【FMCW 01】中频IF信号
FMCW信号
调频连续波(frequency modulated continuous wave,FMCW)顾名思义,就是对信号的频率进行线性调制的信号。
从时域上看,对频率的调制,就像一把连续的锯齿波。其中每一个锯齿叫做一个chirp,其持续的时间叫做chirp的周期(chirp period 或 chirp repetition time);在实际使用中,我们将chirp合并成一帧(frame)进行发送,从而得到物体的速度(或多普勒频偏)信息,是为FMCW信号。
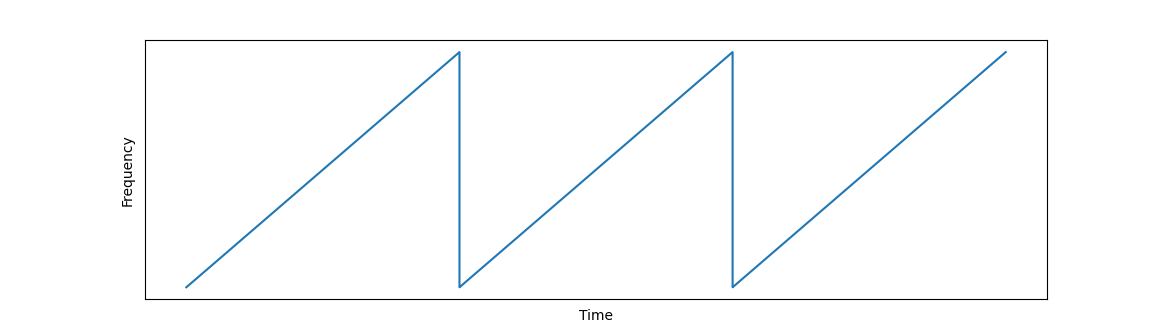
我们定义扫频带宽与chirp周期的比值为系数K,也即锯齿波的斜率(slope)。
K=扫频带宽chirp周期=扫频终止频率−扫频起始频率chirp周期K = \frac{扫频带宽}{chirp周期}= \frac{扫频终止频率-扫频起始频率}{chirp周期} K=chirp周期扫频带宽=chirp周期扫频终止频率−扫频起始频率
如果从时域上看此时信号幅度的变化,可以发现随着时间的推移,对应正弦波的频率会越来越高,即呈现越来越密的特点。
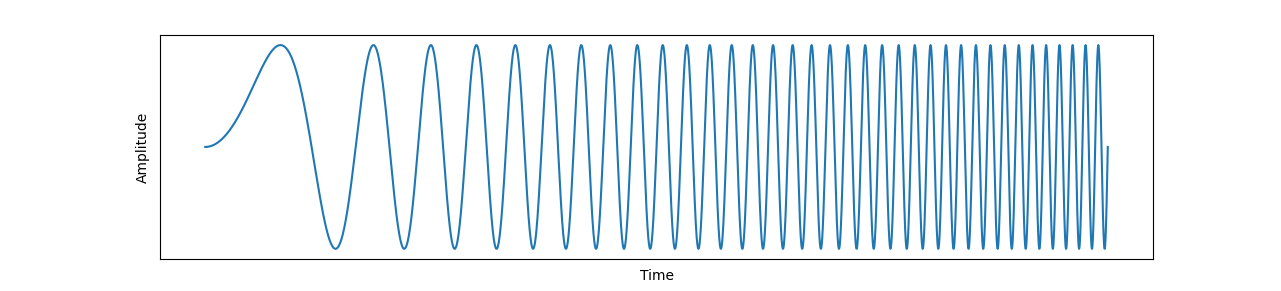
中频信号
我们采用的IF信号就是指接收的回波信号与原始信号进行混频后,再过低通滤波器得到的低中频信号(或差拍信号,beat signal)。用一个简图来表示就是:
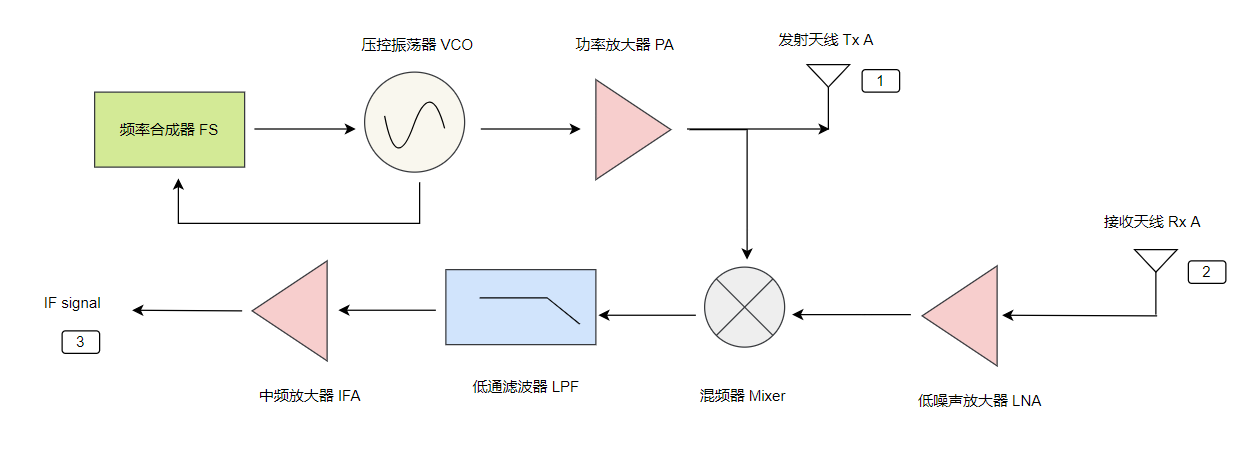
我们只关注1处发射信号、2处接收信号和3处IF信号的表达形式即可。
1处发射信号
由于发送信号为FMCW信号,取其中一个chirp,我们知道相位对时间的导数为角频率(再除以2π2 \pi2π即频率),如下:
12πdϕdt=fo+Kt\frac{1}{2\pi}\frac{d \phi}{dt} = f_o+Kt 2π1dtdϕ=fo+Kt
于是,我们对上式两边积分,就有:
ϕ=2π(fot+12Kt2)+ϕo=2πfot+πKt2+ϕ0\phi = 2\pi( f_ot + \frac{1}{2}Kt^2)+\phi_o = 2\pi f_ot + \pi Kt^2+\phi_0 ϕ=2π(fot+21Kt2)+ϕo=2πfot+πKt2+ϕ0
所以1处发射信号的形式为:
xTx(t)=Asin(2πfot+πKt2+ϕ0)x_{\tiny{T}x}(t) = A \sin(2 \pi f_ot +\pi Kt^2+\phi_0) xTx(t)=Asin(2πfot+πKt2+ϕ0)
注意上式为发送的实信号形式(在物理世界中传输的都是实信号),将其转换为复信号(在信号处理中这可由希尔伯特变换实现),即
xr=Aej(2πfot+πKt2+ϕ0)x_r = Ae^{j(2 \pi f_ot +\pi Kt^2+\phi_0)} xr=Aej(2πfot+πKt2+ϕ0)
其中,K为斜率,ϕo\phi_oϕo为信号的初始相位,f0f_0f0为中心频率:
fo=扫频起始频率+扫频结束频率2f_o =\frac{扫频起始频率+扫频结束频率}{2} fo=2扫频起始频率+扫频结束频率
2处接收信号

发送的信号在遇到目标(Target)后就会反射,从而产生2处接收天线的回波信号,假设这个时延为τ\tauτ,衰减系数为aaa,则
xRx(t)=axTx(t−τ)=A′sin[2πfo(t−τ)+πK(t−τ)2+ϕ0]=Asin[πKt2+2π(fo−Kτ)t+πKτ2−2πfoτ+ϕ0]x_{\tiny{R}x}(t) = a x_{\tiny{T}x}(t-\tau) = A^{\prime} \sin[2 \pi f_o(t-\tau) +\pi K(t-\tau)^2+\phi_0] \\ =A\sin[\pi K t^2 +2\pi (f_o - K \tau)t+\pi K \tau^2-2 \pi f_o \tau + \phi_0] xRx(t)=axTx(t−τ)=A′sin[2πfo(t−τ)+πK(t−τ)2+ϕ0]=Asin[πKt2+2π(fo−Kτ)t+πKτ2−2πfoτ+ϕ0]
3处IF信号
根据三角公式中的积化和差公式,即:
sin(α)sin(β)=12[cos(α−β)−cos(α+β)]\sin(\alpha) \sin(\beta) = \frac{1}{2}[\cos(\alpha - \beta) - \cos(\alpha + \beta) ] sin(α)sin(β)=21[cos(α−β)−cos(α+β)]
于是我们混频后的信号为:
xTx(t)×xRx(t)=12AA′[cos(2πKτt+2πfoτ−πKτ2)−cos(2π(2fo−Kτ)t+...)]x_{\tiny{T}x}(t) \times x_{\tiny{R}x}(t) =\frac{1}{2}AA^{\prime}[\cos(2\pi K\tau t+2\pi f_o \tau-\pi K \tau^2 ) \\- \cos(2\pi(2 f_o-K \tau)t+...)] xTx(t)×xRx(t)=21AA′[cos(2πKτt+2πfoτ−πKτ2)−cos(2π(2fo−Kτ)t+...)]
经过低通滤波器后,结果中的和式将作为高频成分被滤除,而只留下差式中低频的成分,我们再将这个差信号通过中频放大器放大,最终将得到3处的中频信号,即:
xIF(t)=A′′cos(2πKτt+2πfoτ−πKτ2)x_{\tiny{IF}}(t) = A^{\prime \prime} \cos(2\pi K\tau t+2\pi f_o \tau-\pi K \tau^2 ) xIF(t)=A′′cos(2πKτt+2πfoτ−πKτ2)
我们再对上面的参数有一个感性的认识:由于电磁波以光速运动,在前方1m处的目标其时延τ\tauτ的量级大致在10−810^{-8}10−8,f0f_0f0对于毫米波雷达在10910^9109量级,而一般的 K 大概是1GHz除以0.1ms级别,即10−1310^{-13}10−13级。比较两个附加相位:
foτ≈10Kτ2≈10−3f_o \tau \approx 10 \ \ \ K\tau ^2 \approx 10^{-3} foτ≈10 Kτ2≈10−3
所以最后一项的附加相位几乎可以忽略不计,即一般将中频信号的形式写为:
xIF(t)=A′′cos(2πKτt+2πfoτ)x_{\tiny{IF}}(t) = A^{\prime \prime} \cos(2\pi K\tau t+2\pi f_o \tau ) xIF(t)=A′′cos(2πKτt+2πfoτ)
上式即为本文最终要得出的式子。
相关文章:

【FMCW 01】中频IF信号
FMCW信号 调频连续波(frequency modulated continuous wave,FMCW)顾名思义,就是对信号的频率进行线性调制的信号。 从时域上看,对频率的调制,就像一把连续的锯齿波。其中每一个锯齿叫做一个chirp,其持续的时间叫做ch…...

【蓝桥杯试题】暴力枚举题型
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:蓝桥杯试题 文章目录1. 统计方形(数据加强版)1. 1 题目描述1.2 思路…...

I.MX6ULL_Linux_系统篇(22) kernel移植
原厂 Linux 内核编译 NXP 提供的 Linux 源码肯定是可以在自己的 I.MX6ULL EVK 开发板上运行下去的,所以我们肯定是以 I.MX6ULL EVK 开发板为参考,然后将 Linux 内核移植到 I.MX6U-ALPHA 开发板上的。 配置编译 Linux 内核 和uboot一样,在编…...

UE实现相机聚焦物体功能
文章目录 1.实现目标2.实现过程2.1 实现原理2.2 源码浅析2.3 具体代码2.3.1 蓝图实现2.3.2 C++实现3.参考资料1.实现目标 实现根据输入的Actor,自动计算出其缩放显示到当前屏幕上相机的最终位置,然后相机飞行过去,实现相机对物体的聚集效果,避免每次输入FlyTo坐标参数,GI…...
算法系列之数值积分的目的
PLC算法里的数字积分器详细介绍请参看下面的文章链接: PLC算法系列之数值积分器(Integrator)_RXXW_Dor的博客-CSDN博客数值积分和微分在工程上的重要意义不用多说,闭环控制的PID控制器就是积分和微分信号的应用。流量累加也会用到。有关积分运算在流量累加上的应用,请参看下…...

【2.4 golang中循环语句for】
1. 循环语句for 1.1.1. Golang for支持三种循环方式,包括类似 while 的语法。 for循环是一个循环控制结构,可以执行指定次数的循环。 语法 Go语言的For循环有3中形式,只有其中的一种使用分号。 for init; condition; post { }for conditi…...

代码随想录 动态规划||343 96
Day35343. 整数拆分力扣题目链接给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。思路动规逻辑确定dp数组(dp table)以及下标的含义dp[i]指的是拆分数字i能得到的最大成绩d…...
Python---正则表达式
专栏:python 个人主页:HaiFan. 专栏简介:Python在学,希望能够得到各位的支持!!! 正则表达式前言概念作用和特点使用场景正则符号re模块re.compile()match()search()span()findall()group()sub()…...

Unity入门精要02---纹理
纹理和材质不可分割 本节知识结构 实践:简单贴一张纹理到模型上 首先在属性处添加相关属性 Properties {_Color ("Color Tint", Color) (1, 1, 1, 1)_MainTex ("Main Tex", 2D) "white" {}//加入纹理_Specular ("Specular&q…...
【Day1】一小时入门 python 基础,从安装到入门
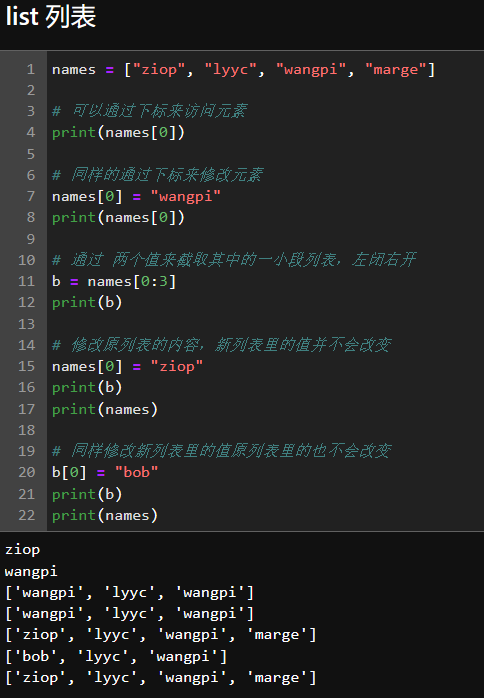
文章目录python安装安装python安装 pycharmpython基础输出注释变量输入类型转换运算符自增字符串相关操作比较运算符逻辑运算符条件控制while循环list 列表for 循环range函数元组python 安装 安装python 官网进行下载:官网下载地址这里下载的一直是最新版本的 点…...

2D图像处理:相机标定
文章目录 效果一、相机标定的是什么?二、四个坐标系2.1 世界坐标系(X,Y,Z)2.2 相机坐标系(x,y,x)2.3 图像坐标系2.4 像素坐标系三、坐标系间的变换关系3.1 世界坐标系-->相机坐标系3.2 相机坐标系-->图像坐标系3.3图像坐标系-->像素坐标系四、相机畸变模型4.1 径向…...
windows 下 python 和repo 下载安装环境变量配置
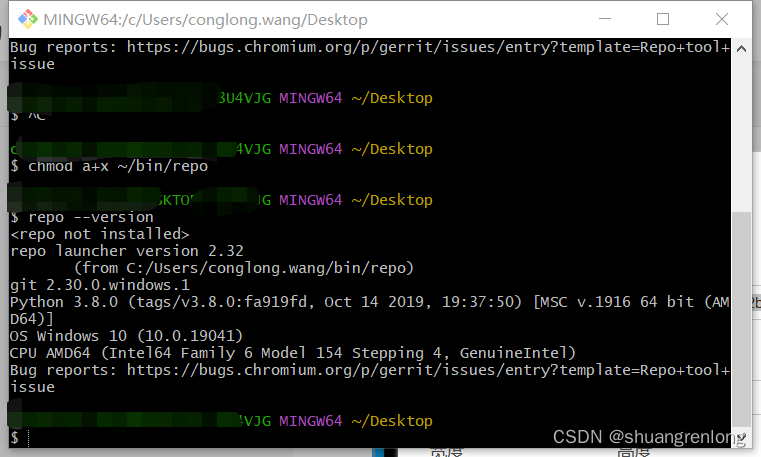
repo 安装成功,但是下载代码 repo init的时候出错 不知道是不是repo windows版本有问题 python 最好下载2.6-2.7版本的 Python Releases for Windows | Python.org 不然下载代码会有问题,下不了,会提示安装2.6-2.7版本的 Windows下成功安…...

jsp进阶
文章目录jsp进阶内容回顾JSP 的九大内置对象内置对象的创建九大内置对象详解四大作用域对象四大作用域范围总结EL 进阶JSTL 标准标签库JSTL 核心标签jsp进阶 内容回顾 jsp 创建 jsp 的工作原理:翻译 --> 编译 --> 运行 翻译:第一次访问 jsp 页面…...

模块化CommonJS、AMD、CMD、ES6
参考链接:https://juejin.cn/post/6844903576309858318 一、 commonjs(node实现、缓存值(浅拷贝),同步,运行时加载) 同步加载模块 module.exportrequire // 定义模块math.js var basicNum …...
Python GUI界面编程-初识
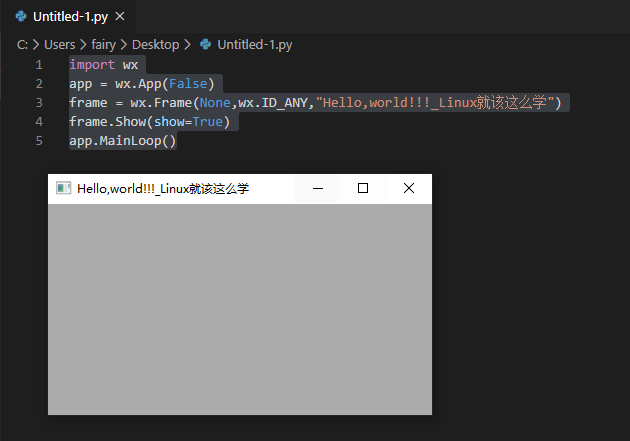
图形用户界面(Graphical User Interface,简称 GUI,又称图形用户接口)是指采用图形方式显示的计算机操作用户界面。与早期计算机使用的命令行界面相比,图形界面对于用户来说在视觉上更易于接受。然而这界面若要通过在显示屏的特定位置…...
【Servlet篇4】cookie和session
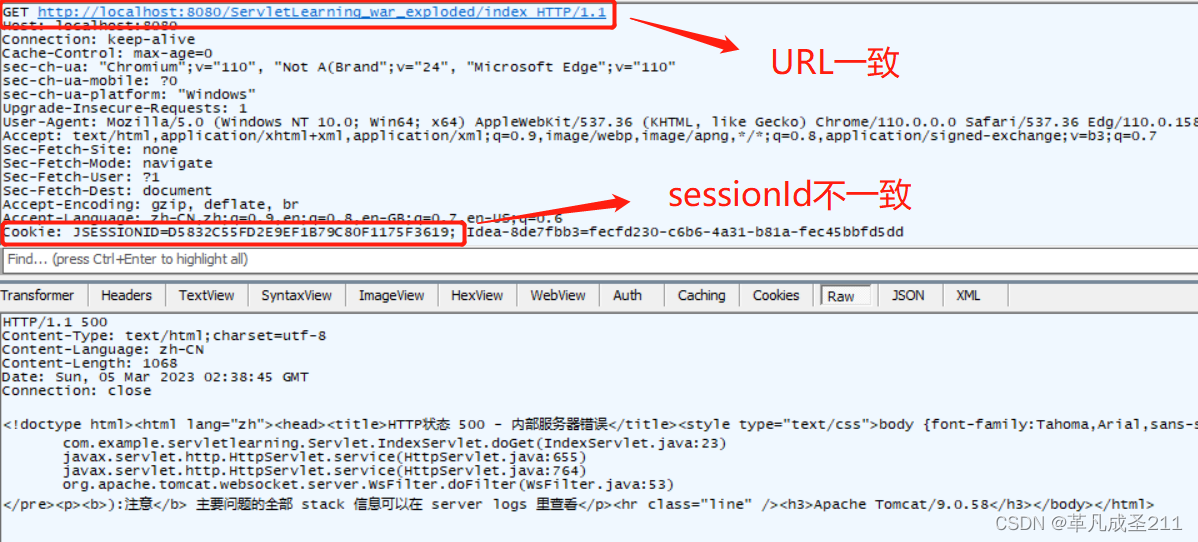
在这一篇文章当中,我们提到了什么是cookie和session。 【网络原理8】HTTP请求篇_革凡成圣211的博客-CSDN博客HTTP的常见属性,URL,User-Agent,Refer,get 和post的区别https://blog.csdn.net/weixin_56738054/article/details/1291…...
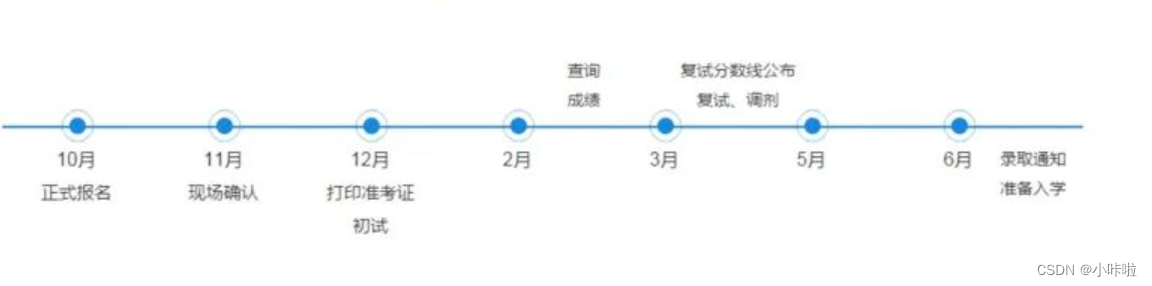
考研流程,可以进来转一转(考研你不知道的事情)(详细版)
之前有听过好多人说要考研,那么,考研的信息,如何获取呢,考研都有哪些流程呢。 初试开始到考试:↓ 1、了解考研信息。 2、确定自己要报考的专业。(本专业or跨考) 3、选择地区 4、选择要报考的学…...
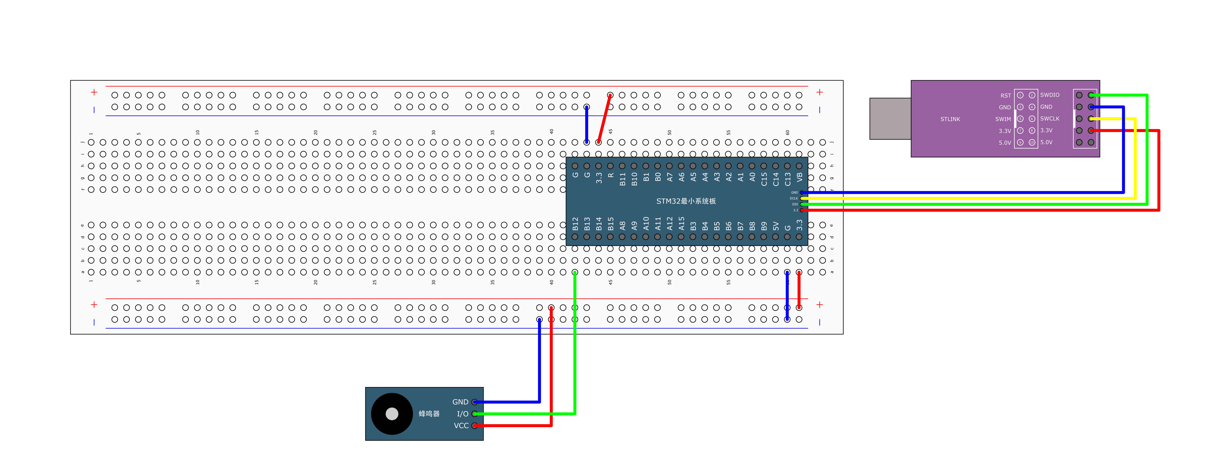
3.2 LED闪烁流水灯蜂鸣器
LED闪烁1.1 电路连接示意图LED采用低电平点亮的方式,利用ST-Link的3.3V进行供电。1.2程序设计1.21知识储备GPIO配置步骤步骤:1. 第⼀步,使⽤RCC开启GPIO的时钟2. 第⼆步,使⽤GPIO_Init()函数初始化GPIO3. 第三步,使⽤输…...

刷题笔记3 | 203. 移除链表元素、707设计链表,206.反转链表
目录 203. 移除链表元素 707、设计链表 206.反转链表 203. 移除链表元素 题意:删除链表中等于给定值 val 的所有节点。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出:[1,2,3,4,5] 示例 2: 输入:h…...

[一篇读懂]C语言十一讲:单链表的删除和单链表真题实战
[一篇读懂]C语言十一讲:单链表的删除和单链表真题实战1. 与408关联解析及本节内容介绍1 本节内容介绍2. 单链表的删除操作实战3. 单链表真题解读与解题设计1 题目解读2 解题设计第一阶段:双指针找中间结点第二阶段:原地逆置第三阶段ÿ…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
