《动手学深度学习(PyTorch版)》笔记4.1
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过。
Chapter4 Multilayer Perceptron
4.1 Basic Concepts
4.1.1 Hidden Layer
我们在第三章中描述了仿射变换,它是一种带有偏置项的线性变换。如果我们的标签通过仿射变换后确实与我们的输入数据相关,那么这种方法确实足够了。但是,仿射变换中的线性是一个很强的假设。线性意味着单调假设:任何特征的增大都会导致模型输出的增大(如果对应的权重为正),或者导致模型输出的减小(如果对应的权重为负)。有时这是有道理的。例如,如果我们试图预测一个人是否会偿还贷款。我们可以认为,在其他条件不变的情况下,收入较高的申请人比收入较低的申请人更有可能偿还贷款。但是,虽然收入与还款概率存在单调性,但它们不是线性相关的。收入从0增加到5万,可能比从100万增加到105万带来更大的还款可能性。处理这一问题的一种方法是对我们的数据进行预处理,使线性变得更合理,如使用收入的对数作为我们的特征。
然而我们可以很容易找出违反单调性的例子。例如,我们想要根据体温预测死亡率。对体温高于37摄氏度的人来说,温度越高风险越大。然而,对体温低于37摄氏度的人来说,温度越高风险就越低。在这种情况下,我们也可以通过一些巧妙的预处理来解决问题。例如,我们可以使用与37摄氏度的距离作为特征。
与我们前面的例子相比,这里的线性很荒谬,而且我们难以通过简单的预处理来解决这个问题。我们的数据可能会有一种表示,这种表示会考虑到我们在特征之间的相关交互作用。在此表示的基础上建立一个线性模型可能会是合适的,但我们不知道如何手动计算这么一种表示。对于深度神经网络,我们使用观测数据来联合学习隐藏层表示和应用于该表示的线性预测器。
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制,使其能处理更普遍的函数关系类型。要做到这一点,最简单的方法是将许多全连接层堆叠在一起。每一层都输出到上面的层,直到生成最后的输出。我们可以把前 L − 1 L-1 L−1层看作表示,把最后一层看作线性预测器。这种架构通常称为多层感知机(multilayer perceptron),通常缩写为MLP,下面我们以图的方式描述了多层感知机。

这个多层感知机有4个输入,3个输出,其隐藏层包含5个隐藏单元。输入层不涉及任何计算,因此使用此网络产生输出只需要实现隐藏层和输出层的计算。因此,这个多层感知机中的层数为2。注意,这两个层都是全连接的。每个输入都会影响隐藏层中的每个神经元,而隐藏层中的每个神经元又会影响输出层中的每个神经元。
然而,具有全连接层的多层感知机的参数开销可能会高得令人望而却步,即使在不改变输入或输出大小的情况下,可能在参数节约和模型有效性之间进行权衡。
同之前的章节一样,我们通过矩阵 X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d来表示 n n n个样本的小批量,其中每个样本具有 d d d个输入特征。对于具有 h h h个隐藏单元的单隐藏层多层感知机,用 H ∈ R n × h \mathbf{H} \in \mathbb{R}^{n \times h} H∈Rn×h表示隐藏层的输出,称为隐藏表示(hidden representations)。在数学或代码中, H \mathbf{H} H也被称为隐藏层变量(hidden-layer variable)或隐藏变量(hidden variable)。因为隐藏层和输出层都是全连接的,所以我们有隐藏层权重 W ( 1 ) ∈ R d × h \mathbf{W}^{(1)} \in \mathbb{R}^{d \times h} W(1)∈Rd×h和隐藏层偏置 b ( 1 ) ∈ R 1 × h \mathbf{b}^{(1)} \in \mathbb{R}^{1 \times h} b(1)∈R1×h以及输出层权重 W ( 2 ) ∈ R h × q \mathbf{W}^{(2)} \in \mathbb{R}^{h \times q} W(2)∈Rh×q和输出层偏置 b ( 2 ) ∈ R 1 × q \mathbf{b}^{(2)} \in \mathbb{R}^{1 \times q} b(2)∈R1×q。形式上,我们按如下方式计算单隐藏层多层感知机的输出 O ∈ R n × q \mathbf{O} \in \mathbb{R}^{n \times q} O∈Rn×q:
H = X W ( 1 ) + b ( 1 ) , O = H W ( 2 ) + b ( 2 ) . \begin{aligned} \mathbf{H} & = \mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}, \\ \mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}. \end{aligned} HO=XW(1)+b(1),=HW(2)+b(2).
注意在添加隐藏层之后,模型现在需要跟踪和更新额外的参数。可我们能从中得到什么好处呢?在上面定义的模型里,我们没有好处!原因很简单:上面的隐藏单元由输入的仿射函数给出,而输出(softmax操作前)只是隐藏单元的仿射函数。仿射函数的仿射函数本身就是仿射函数,但是我们之前的线性模型已经能够表示任何仿射函数。对于这个例子,证明如下:
O = ( X W ( 1 ) + b ( 1 ) ) W ( 2 ) + b ( 2 ) = X W ( 1 ) W ( 2 ) + b ( 1 ) W ( 2 ) + b ( 2 ) = X W + b . \mathbf{O} = (\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})\mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W}^{(1)}\mathbf{W}^{(2)} + \mathbf{b}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W} + \mathbf{b}. O=(XW(1)+b(1))W(2)+b(2)=XW(1)W(2)+b(1)W(2)+b(2)=XW+b.
为了发挥多层架构的潜力,我们还需要一个额外的关键要素:在仿射变换之后对每个隐藏单元应用非线性的激活函数(activation function) σ \sigma σ。激活函数的输出(例如, σ ( ⋅ ) \sigma(\cdot) σ(⋅))被称为活性值(activations)。一般来说,有了激活函数,就不可能再将我们的多层感知机退化成线性模型:
H = σ ( X W ( 1 ) + b ( 1 ) ) , O = H W ( 2 ) + b ( 2 ) . \begin{aligned} \mathbf{H} & = \sigma(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}), \\ \mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}.\\ \end{aligned} HO=σ(XW(1)+b(1)),=HW(2)+b(2).
由于 X \mathbf{X} X中的每一行对应于小批量中的一个样本,出于记号习惯的考量,我们定义非线性函数 σ \sigma σ也以按行的方式作用于其输入,即一次计算一个样本。本节应用于隐藏层的激活函数通常不仅按行操作,也按元素操作。这意味着在计算每一层的线性部分之后,我们可以计算每个活性值,而不需要查看其他隐藏单元所取的值,对于大多数激活函数都是这样。
为了构建更通用的多层感知机,我们可以继续堆叠这样的隐藏层,例如 H ( 1 ) = σ 1 ( X W ( 1 ) + b ( 1 ) ) \mathbf{H}^{(1)} = \sigma_1(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}) H(1)=σ1(XW(1)+b(1))和 H ( 2 ) = σ 2 ( H ( 1 ) W ( 2 ) + b ( 2 ) ) \mathbf{H}^{(2)} = \sigma_2(\mathbf{H}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)}) H(2)=σ2(H(1)W(2)+b(2)),一层叠一层,从而产生更有表达能力的模型。
多层感知机可以通过隐藏神经元,捕捉到输入之间复杂的相互作用,这些神经元依赖于每个输入的值。我们可以很容易地设计隐藏节点来执行任意计算。例如,在一对输入上进行基本逻辑操作,多层感知机是通用近似器。即使是网络只有一个隐藏层,给定足够的神经元和正确的权重,我们可以对任意函数建模,尽管实际中学习该函数是很困难的(通用近似定理)
虽然一个单隐层网络能学习任何函数,但并不意味着我们应该尝试使用单隐藏层网络来解决所有问题。事实上,通过使用更深(而不是更广)的网络,我们可以更容易地逼近许多函数。我们将在后面的章节中进行更细致的讨论。
4.1.2 Activation Function
激活函数(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活,它们将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。激活函数是深度学习的基础,下面介绍一些常见的激活函数。
4.1.2.1 ReLU function
最受欢迎的激活函数是修正线性单元(Rectified linear unit,ReLU),因为它实现简单,同时在各种预测任务中表现良好。ReLU提供了一种非常简单的非线性变换,给定元素 x x x,ReLU函数被定义为该元素与 0 0 0的最大值:
ReLU ( x ) = max ( x , 0 ) . \operatorname{ReLU}(x) = \max(x, 0). ReLU(x)=max(x,0).
如图,激活函数是分段线性的。

当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。注意,当输入值精确等于0时,ReLU函数不可导。在此时,我们默认使用左侧的导数,即当输入为0时导数为0。我们可以忽略这种情况,因为输入可能永远都不会是0,正如一句名言所说,“如果微妙的边界条件很重要,我们很可能是在研究数学而非工程”。ReLU函数的导数图像如下:

使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题(稍后将详细介绍)。
ReLU函数有许多变体,包括参数化ReLU(Parameterized ReLU,pReLU)函数,该变体为ReLU添加了一个线性项,因此即使参数是负的,某些信息仍然可以通过:
pReLU ( x ) = max ( 0 , x ) + α min ( 0 , x ) . \operatorname{pReLU}(x) = \max(0, x) + \alpha \min(0, x). pReLU(x)=max(0,x)+αmin(0,x).
4.1.2.2 Sigmoid function
sigmoid通常称为挤压函数(squashing function),因为它将范围(-inf, inf)中的任意输入压缩到区间(0, 1)中的某个值:
sigmoid ( x ) = 1 1 + exp ( − x ) . \operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)}. sigmoid(x)=1+exp(−x)1.
当人们逐渐关注到到基于梯度的学习时,sigmoid函数是一个自然的选择,因为它是一个平滑的、可微的阈值单元近似。当我们想要将输出视作二元分类问题的概率时,sigmoid仍然被广泛用作输出单元上的激活函数(sigmoid可以视为softmax的特例)。然而,sigmoid在隐藏层中已经较少使用,
它在大部分时候被更简单、更容易训练的ReLU所取代。在后面关于循环神经网络的章节中,我们将描述利用sigmoid单元来控制时序信息流的架构。
sigmoid函数图像如下:

sigmoid函数的导数为:
d d x sigmoid ( x ) = exp ( − x ) ( 1 + exp ( − x ) ) 2 = sigmoid ( x ) ( 1 − sigmoid ( x ) ) . \frac{d}{dx} \operatorname{sigmoid}(x) = \frac{\exp(-x)}{(1 + \exp(-x))^2} = \operatorname{sigmoid}(x)\left(1-\operatorname{sigmoid}(x)\right). dxdsigmoid(x)=(1+exp(−x))2exp(−x)=sigmoid(x)(1−sigmoid(x)).
sigmoid函数的导数图像如下:

4.1.2.3 tanh function
与sigmoid函数类似,tanh(双曲正切)函数能将其输入压缩转换到区间(-1, 1)上。tanh函数的公式如下:
tanh ( x ) = 1 − exp ( − 2 x ) 1 + exp ( − 2 x ) . \operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}. tanh(x)=1+exp(−2x)1−exp(−2x).
tanh函数的形状类似于sigmoid函数,不同的是tanh函数关于坐标系原点中心对称。其函数图像如下:

tanh函数的导数是:
d d x tanh ( x ) = 1 − tanh 2 ( x ) . \frac{d}{dx} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x). dxdtanh(x)=1−tanh2(x).
tanh函数的导数图像如下:

本节代码如下:
import matplotlib.pyplot as plt
import torch
from d2l import torch as d2l#绘制ReLU函数图像
x=torch.arange(-8,8,0.1,requires_grad=True)
y=torch.relu(x)
d2l.plot(x.detach(),y.detach(),'x','relu(x)',figsize=(5,2.5))
#"detach()" is used to create a new tensor that shares the same data with x but doesn't have a computation graph
plt.show()#绘制ReLU函数的导数图像
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(),x.grad,'x','grad of relu(x)',figsize=(5,2.5))
#torch.ones_like(x): creates a tensor of the same shape as x but filled with ones. This tensor is used as the gradient of the output y with respect to x during backpropagation
#retain_graph=True: retains the computational graph after performing the backward pass
plt.show()#绘制sigmoid函数图像
y=torch.sigmoid(x)
d2l.plot(x.detach(),y.detach(),'x','sigmoid(x)',figsize=(5,2.5))
plt.show()#绘制sigmoid函数的导数图像
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(),x.grad,'x','grad of sigmoid(x)',figsize=(5,2.5))
plt.show()#绘制tanh函数图像
y=torch.tanh(x)
d2l.plot(x.detach(),y.detach(),'x','tanh(x)',figsize=(5,2.5))
plt.show()#绘制tanh函数的导数图像
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(),x.grad,'x','grad of tanh(x)',figsize=(5,2.5))
plt.show()
相关文章:

《动手学深度学习(PyTorch版)》笔记4.1
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过。…...

OpenAI发布新模型!ChatGPT性能重磅提升,API大幅降价,GPT-4 「变懒」被修复
OpenAI 对ChatGPT进行了大更新:推出了新一代的嵌入模型,对GPT-4 Turbo模型进行了更新,并将很快对GPT-3.5 Turbo的API进行大幅降价,GPT-4「变懒」行为也被修复。 接下来二狗就带大家看看ChatGPT的这次详细更新。 推出新的嵌入模型…...
【C深度解剖】计算机数据下载和删除原理
简介:本系列博客为C深度解剖系列内容,以某个点为中心进行相关详细拓展 适宜人群:已大体了解C语法同学 作者留言:本博客相关内容如需转载请注明出处,本人学疏才浅,难免存在些许错误,望留言指正 作…...

ASTORS国土安全奖:ManageEngine AD360荣获银奖
美国安全今日(AST)的年度“ASTORS”国土安全奖计划是一个备受瞩目的活动,致力于突显国土安全领域的创新与进步。这一奖项旨在表彰在保护国家免受安全威胁方面做出卓越贡献的个人和组织。该计划汇聚了执法、公共安全和行业领袖,不仅…...

clang--cpplint--gitlint
clang_format clang_format是什么 代码格式化工具 clang_format 官网和官网教程 中文教程 下载 sudo apt install clang sudo apt install clang-format#查看下载是否成功 clang --version 代码的构建到提交的过程: cmake .. make make test make clang_f…...

Web开发8:前后端分离开发
在现代的 Web 开发中,前后端分离开发已经成为了一种常见的架构模式。它的优势在于前端和后端可以独立开发,互不干扰,同时也提供了更好的可扩展性和灵活性。本篇博客将介绍前后端分离开发的概念、优势以及如何实现。 什么是前后端分离开发&am…...
基于 java+springboot+mybatis电影售票网站管理系统前台+后台设计和实现
基于 javaspringbootmybatis电影售票网站管理系统前台后台设计和实现 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承…...
】错误:*.onchip_flash_0:UFM 扇区不支持“隐藏”模式。请更新访问模式设置)
【INTEL(ALTERA)】错误:*.onchip_flash_0:UFM 扇区不支持“隐藏”模式。请更新访问模式设置
说明 由于英特尔 Quartus Prime Standard Edition 软件版本 22.1 存在一个问题,当您针对 10 FPGA Compact 变体英特尔 MAX在片上闪存英特尔 FPGA IP中选择单压缩映像配置模式时,可能会出现以下错误消息。 错误:*.onchip_flash_0:…...

备战蓝桥杯---数据结构与STL应用(基础3)
今天我们主要介绍的是pair,string,set,map pair:我们可以把它当作一个结构体: void solve(){pair<int int> a;//创建amake_pair(1,2);//添加元素cout<<a.first<<endl<<a.second<<endl;}//输出 当然,它也可以嵌套&#…...

「优选算法刷题」:只出现一次的数字Ⅲ
一、题目 给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。 你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。 示例 1: …...
Vue-43、Vue中组件自定义事件
1、给学生绑定atguigu事件 2、在组件内触发事件 第二种写法 传多个参数。 解绑 解绑一个事件 解绑多个自定义事件 this.$off([xxx1,xxx2]);解绑所有事件 this.$off();总结...

GitHub 开启 2FA 双重身份验证的方法
为什么要开启 2FA 自2023年3月13日起,我们登录 GitHub 都会看到一个要求 Enable 2FA 的重要提示,具体如下: GitHub users are now required to enable two-factor authentication as an additional security measure. Your activity on GitHub includes you in this requi…...
ASP.NET Core 过滤器 使用依赖项注入
过滤器是 ASP.NET Core 中的特殊组件,允许我们在请求管道的特定阶段控制请求的执行。这些过滤器在中间件执行后以及 MVC 中间件匹配路由并调用特定操作时发挥作用。 简而言之,过滤器提供了一种在操作级别自定义应用程序行为的方法。它们就像检查点&#…...

2024年的网创之路应该这样走才对
2024年的网创之路应该这样走才对 大家都知道这两年经济环境不好,钱不好挣,对于普通人,只有一条出路,就是学某项技能,然后死磕,不能提升某项技能的项目,打死也不做,因为多数项目都是…...

ssh异常报错:Did not receive identification string from
一、问题描述 某次外出在异地工作场所xshell炼乳远程服务器时,报错:Connection closed by foreign host. D,服务器查看secure日志或sshd服务状态会显示:id not receive identification string from client_ip; 二、分析处理 1&a…...
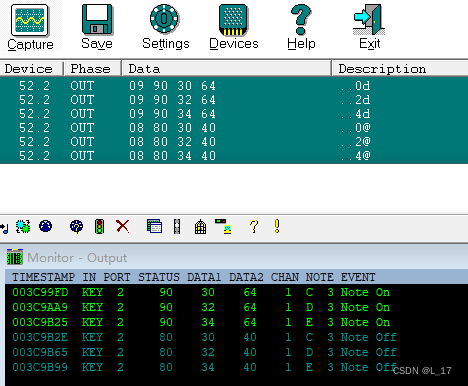
MIDI码深度解析
MIDI 协议即数字音乐接口(Musical Instrument Digital Interface),是电子乐器、合成器等演奏设备之间的一种即时通信协议,用于硬件之间的实时演奏数据传递。如果理解还不够深刻,官方如下解释: 常用midi硬件…...
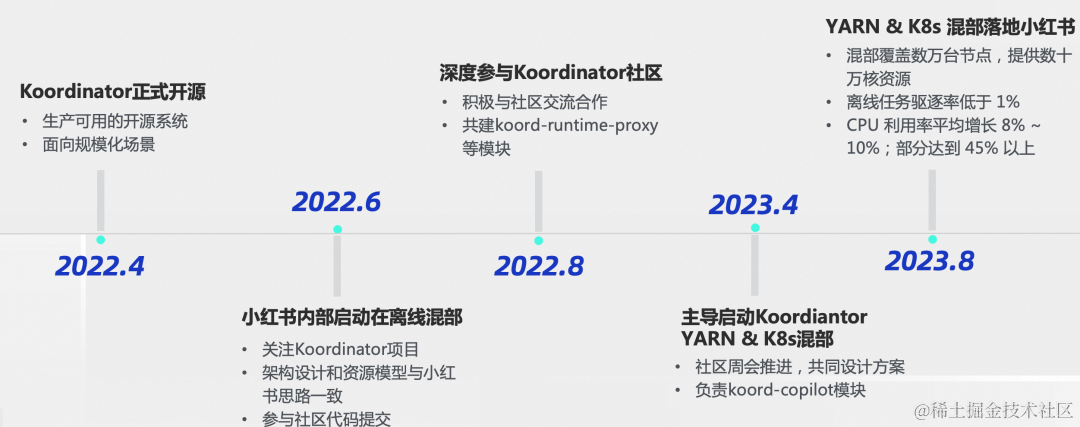
小红书如何做混部?
作者:宋泽辉(小红书)、张佐玮(阿里云) 编者按: Koordinator 是一个开源项目,是基于阿里巴巴内部多年容器调度、混部实践经验孵化诞生,是行业首个生产可用、面向大规模场景的开源混…...
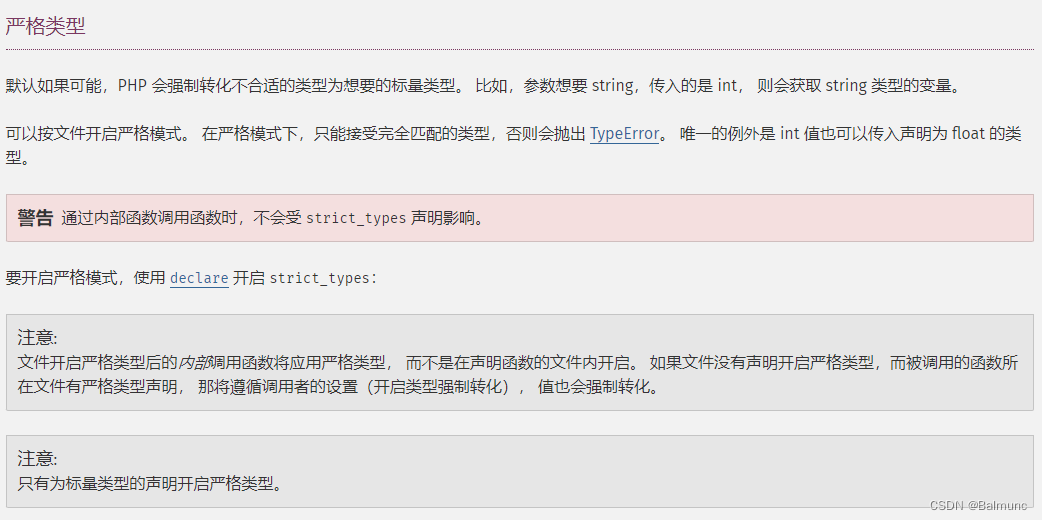
[PHP]严格类型
PHP: 类型声明 - Manual...

作为程序员,你必须学会Maven
资源领取在末尾. Maven 是一款旨在简化 Java 开发流程的管理工具,它的主要功能包括: 1. 项目管理:Maven 提供了一种项目对象模型(Project Object Model, POM),用于管理项目的构建、报告和文档。它允许开发者通过少量代码…...
数据访问宏)
UDF学习(三)数据访问宏
数据访问宏一 网格节点相关宏** NODE_X (v) 节点v的x方向的坐标 (Node *v) NODE_Y (v) 节点v的y方向的坐标 (Node *v) NODE_Z (v) 节点v的z方向的坐标 (Node *v) F_NODE (f,t,n) 获取节点 (face_t f, Thread *t, int n 节点索引号) F_NNODES(f,t) 获取面上的节点数量 (…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

DriveGPT4: Interpretable End-to-end Autonomous Driving via Large Language Model
一、研究背景与创新点 (一)现有方法的局限性 当前智驾系统面临两大核心挑战:一是长尾问题,即系统在遇到新场景时可能失效,例如突发交通状况或非常规道路环境;二是可解释性问题,传统方法无法解释智驾系统的决策过程,用户难以理解车辆行为的依据。传统语言模型(如 BERT…...

年度峰会上,抖音依靠人工智能和搜索功能吸引广告主
上周早些时候举行的第五届年度TikTok World产品峰会上,TikTok推出了一系列旨在增强该应用对广告主吸引力的功能。 新产品列表的首位是TikTok Market Scope,这是一个全新的分析平台,为广告主提供整个考虑漏斗的全面视图,使他们能够…...
