【MAC】Multi-Level Monte Carlo Actor-Critic阅读笔记
基本思想:
利用多层次蒙特卡洛方法(Multi-Level Monte Carlo,MLMC)和Actor-Critic算法,解决平均奖励强化学习中的快速混合问题。
快速混合?
在强化学习中,当我们说一个策略"混合得快",是指该策略在探索和利用之间达到一个良好的平衡,从而使学习过程更快、更有效。
提出的背景:
现有的强化学习方法在后端使用的是stochastic gradient descent(随机梯度下降),基于数据生成过程与步长选择中出现的速率参数以指数速度混合的假设,但对于较大状态空间或具有稀疏奖励的情况,这个假设并不成立。因此提出MAC这一个方法,是将蒙特卡洛利用于critic网络,actor网络和AC算法中的平均奖励,既不依赖于参数选择中混合时间的预测知识,也不假定其指数衰减。
随机梯度下降 (Stochastic Gradient Descent,SGD) 是一种选代优化算法,用于最小化代价函数J(theta)。该算法在每次迭代时随机选择一个训练样本,并利用该样本对模型参数theta进行更新然后重复这个过程多次。
混合速率?
如果环境是高度随机性的或存在很多障碍,这时智能体可能会长期停留在固定的一个状态下,到达稳态的总变化的变化距离是在缓慢减小的,也就是mixing rate,混合速率较慢。
许多强化学习的环境由于高纬度、内在波动性、稀疏奖励或包含不同的子任务导致它们表现出比指数级环境更慢的混合速率。
论文中关于mixing time的定义是:
主要思路:
将多层次蒙特卡洛方法与Actor-Critic算法相结合,通过同时更新策略和状态-行为值函数来寻找最优策略。在多层次蒙特卡洛方法中,Actor部分使用低层次的蒙特卡洛模拟来快速更新策略,而Critic部分使用高层次的蒙特卡洛模拟来精确计算状态-行为值函数的更新。
MAC算法的伪代码:

与传统AC算法不同的是,中间利用了MLMC算法,即多层次蒙特卡洛方法,对参数进行更新。
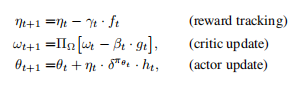
论文作者是在Dorman&Levy所研究出的MLMC和AdaGrad步长选择器基础上开发出一个MLMC梯度估计器。
Adagrad优化算法被称为自适应学习率优化算法,之前我们讲的随机梯度下降对所有的参数都使用的固定的学习率进行参数更新,但是不同的参数梯度可能不一样,所以需要不同的学习率才能比较好的进行训练,但Adagrad 的核心想法就是,如果一个参数的梯度一直都非常大,那么其对应的学习率就变小一点,防止震荡,而一个参数的梯度一直都非常小,那么这个参数的学习率就变大一点,使得其能够更快地更新。
论文实验:
算法环境是一个NxN网格,起始位置在左上角,目标位置在右下角。智能体有五个动作:停留、上、下、左和右,到达目标位置给予+1奖励,其余位置为0奖励。
相关文章:
【MAC】Multi-Level Monte Carlo Actor-Critic阅读笔记
基本思想: 利用多层次蒙特卡洛方法(Multi-Level Monte Carlo,MLMC)和Actor-Critic算法,解决平均奖励强化学习中的快速混合问题。 快速混合? 在强化学习中,当我们说一个策略"混合得快"…...

[GN] 设计模式—— 创建型模式
文章目录 创建型模式单例模式 -- 确保对象唯一性例子优化饿汉式懒汉式 优缺点使用场景 简单工厂模式例子:优化优缺点适用场景 工厂方法模式 -- 多态工厂的实现例子优缺点优化适用场景 抽象工厂模式 -- 产品族的创建例子优缺点适用场景 总结 创建型模式 单例模式 –…...

链表——超详细
一、无头单向非循环链表 1.结构(两个部分): typedef int SLTDataType; typedef struct SListNode {SLTDataType data;//数据域struct SListNode* next;//指针域 }SLNode; 它只有一个数字域和一个指针域,里面数据域就是所存放的…...
【刷题】 leetcode 面试题 08.05.递归乘法
递归乘法 1 题目描述2 思路一(返璞归真版)3 思路二(二进制乘法器版)4 思路三(变态版)Thanks♪(・ω・)ノ谢谢阅读下一篇文章见!!! 1 题目…...
C语言实现希尔排序算法(附带源代码)
希尔排序 希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。 希尔排序是基于插入排序的以下两点性质而提出改进方法的: 插入排序在对几乎已经排好序的数据操作时,效率高࿰…...
:取taxlist对象的子集)
R语言【taxlist】——subset():取taxlist对象的子集
Package taxlist version 0.2.4 Description taxlist对象的子集将通过逻辑操作或模式匹配来完成。子集可以引用包含在插槽taxonNames、taxonRelations或taxonTraits中的信息。 Usage ## S4 method for signature taxlist subset(x,subset,slot "names",keep_child…...

单片机学习笔记---定时器计数器(含寄存器)工作原理介绍(详解篇2)
目录 T1工作在方式2时 T0工作在方式3时 四种工作方式的总结 定时计数器对输入信号的要求 定时计数器对的编程的一个要求 关于初值计算的问题 4种工作方式的最大定时时间的大小 关于编程方式的问题 实例分析 实例1 实例2 T1工作在方式2时 51单片机,有两个…...

《动手学深度学习(PyTorch版)》笔记4.1
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过。…...

OpenAI发布新模型!ChatGPT性能重磅提升,API大幅降价,GPT-4 「变懒」被修复
OpenAI 对ChatGPT进行了大更新:推出了新一代的嵌入模型,对GPT-4 Turbo模型进行了更新,并将很快对GPT-3.5 Turbo的API进行大幅降价,GPT-4「变懒」行为也被修复。 接下来二狗就带大家看看ChatGPT的这次详细更新。 推出新的嵌入模型…...
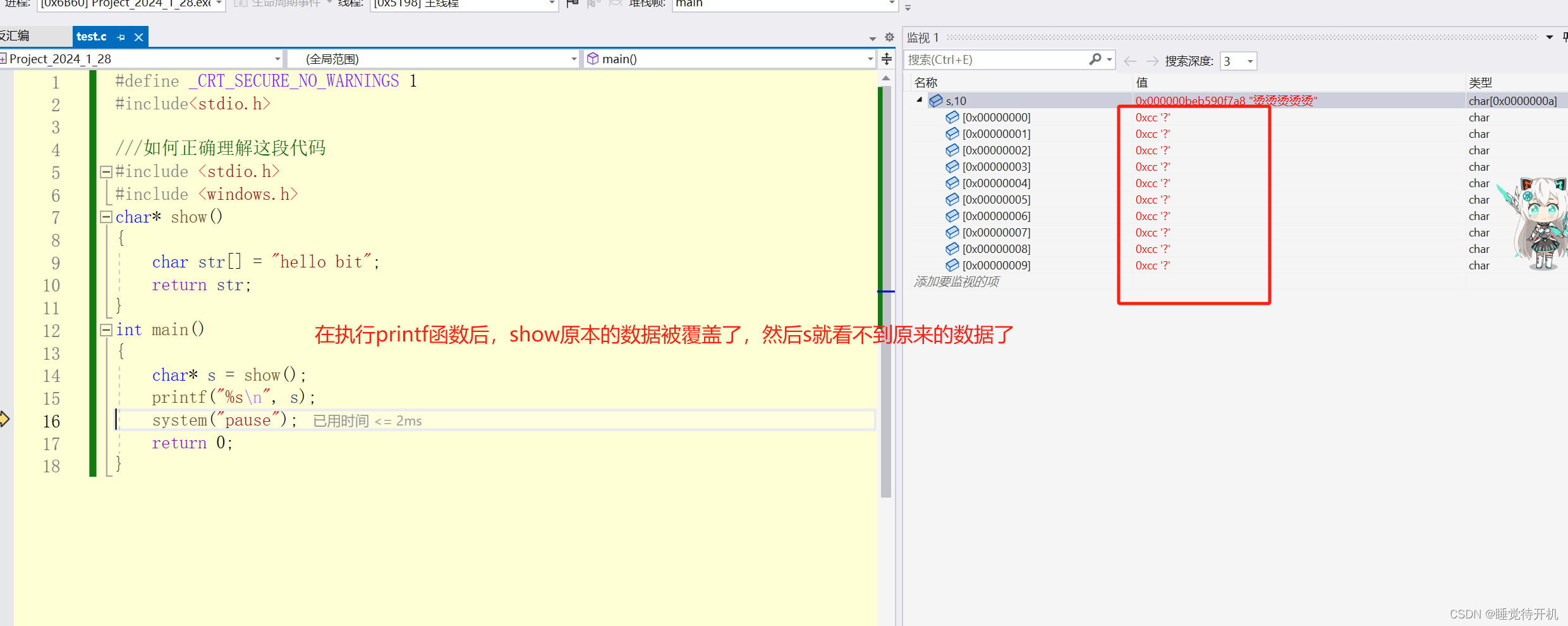
【C深度解剖】计算机数据下载和删除原理
简介:本系列博客为C深度解剖系列内容,以某个点为中心进行相关详细拓展 适宜人群:已大体了解C语法同学 作者留言:本博客相关内容如需转载请注明出处,本人学疏才浅,难免存在些许错误,望留言指正 作…...

ASTORS国土安全奖:ManageEngine AD360荣获银奖
美国安全今日(AST)的年度“ASTORS”国土安全奖计划是一个备受瞩目的活动,致力于突显国土安全领域的创新与进步。这一奖项旨在表彰在保护国家免受安全威胁方面做出卓越贡献的个人和组织。该计划汇聚了执法、公共安全和行业领袖,不仅…...

clang--cpplint--gitlint
clang_format clang_format是什么 代码格式化工具 clang_format 官网和官网教程 中文教程 下载 sudo apt install clang sudo apt install clang-format#查看下载是否成功 clang --version 代码的构建到提交的过程: cmake .. make make test make clang_f…...

Web开发8:前后端分离开发
在现代的 Web 开发中,前后端分离开发已经成为了一种常见的架构模式。它的优势在于前端和后端可以独立开发,互不干扰,同时也提供了更好的可扩展性和灵活性。本篇博客将介绍前后端分离开发的概念、优势以及如何实现。 什么是前后端分离开发&am…...
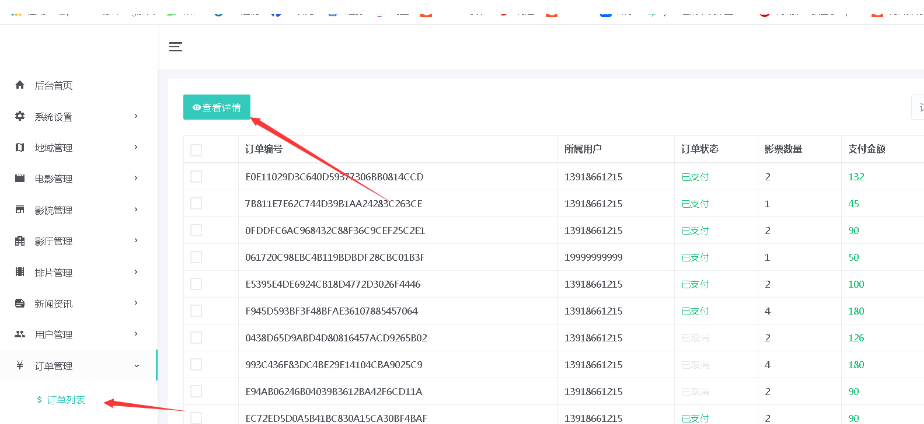
基于 java+springboot+mybatis电影售票网站管理系统前台+后台设计和实现
基于 javaspringbootmybatis电影售票网站管理系统前台后台设计和实现 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承…...
】错误:*.onchip_flash_0:UFM 扇区不支持“隐藏”模式。请更新访问模式设置)
【INTEL(ALTERA)】错误:*.onchip_flash_0:UFM 扇区不支持“隐藏”模式。请更新访问模式设置
说明 由于英特尔 Quartus Prime Standard Edition 软件版本 22.1 存在一个问题,当您针对 10 FPGA Compact 变体英特尔 MAX在片上闪存英特尔 FPGA IP中选择单压缩映像配置模式时,可能会出现以下错误消息。 错误:*.onchip_flash_0:…...

备战蓝桥杯---数据结构与STL应用(基础3)
今天我们主要介绍的是pair,string,set,map pair:我们可以把它当作一个结构体: void solve(){pair<int int> a;//创建amake_pair(1,2);//添加元素cout<<a.first<<endl<<a.second<<endl;}//输出 当然,它也可以嵌套&#…...

「优选算法刷题」:只出现一次的数字Ⅲ
一、题目 给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。 你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。 示例 1: …...
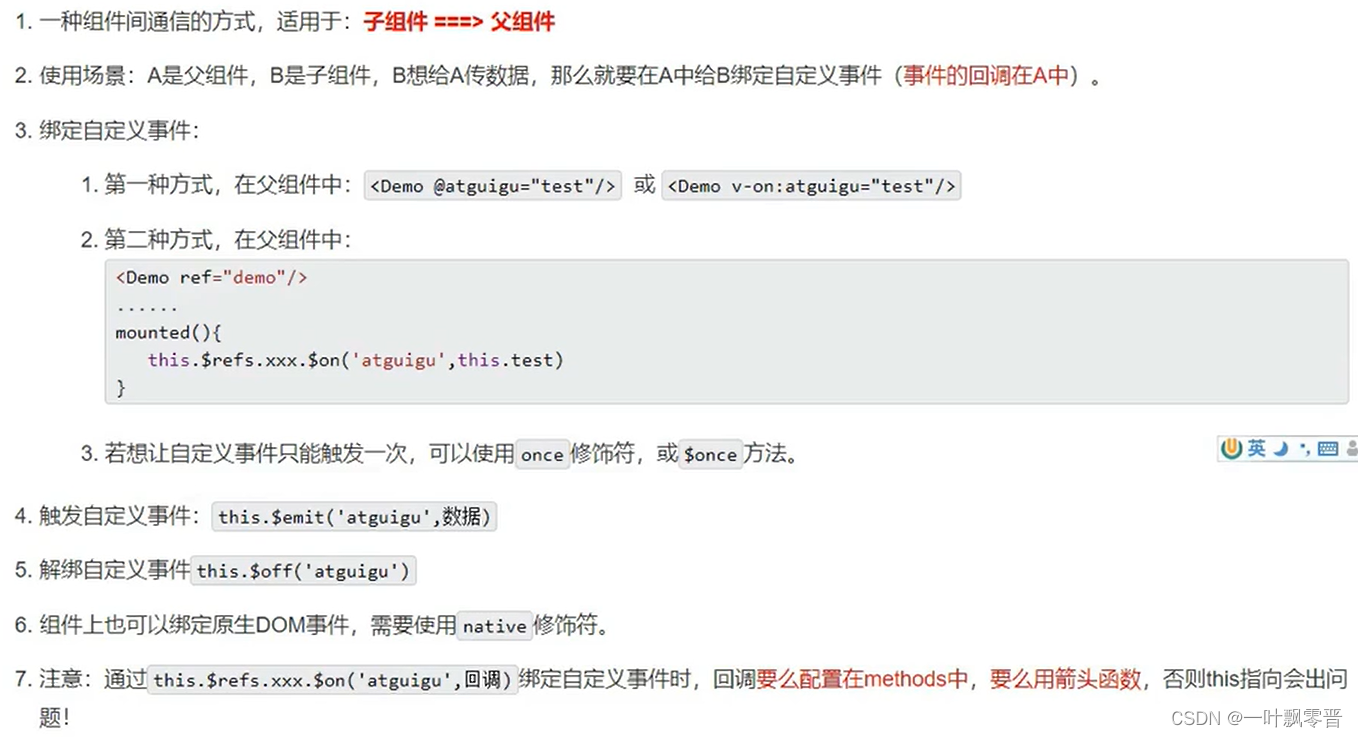
Vue-43、Vue中组件自定义事件
1、给学生绑定atguigu事件 2、在组件内触发事件 第二种写法 传多个参数。 解绑 解绑一个事件 解绑多个自定义事件 this.$off([xxx1,xxx2]);解绑所有事件 this.$off();总结...

GitHub 开启 2FA 双重身份验证的方法
为什么要开启 2FA 自2023年3月13日起,我们登录 GitHub 都会看到一个要求 Enable 2FA 的重要提示,具体如下: GitHub users are now required to enable two-factor authentication as an additional security measure. Your activity on GitHub includes you in this requi…...
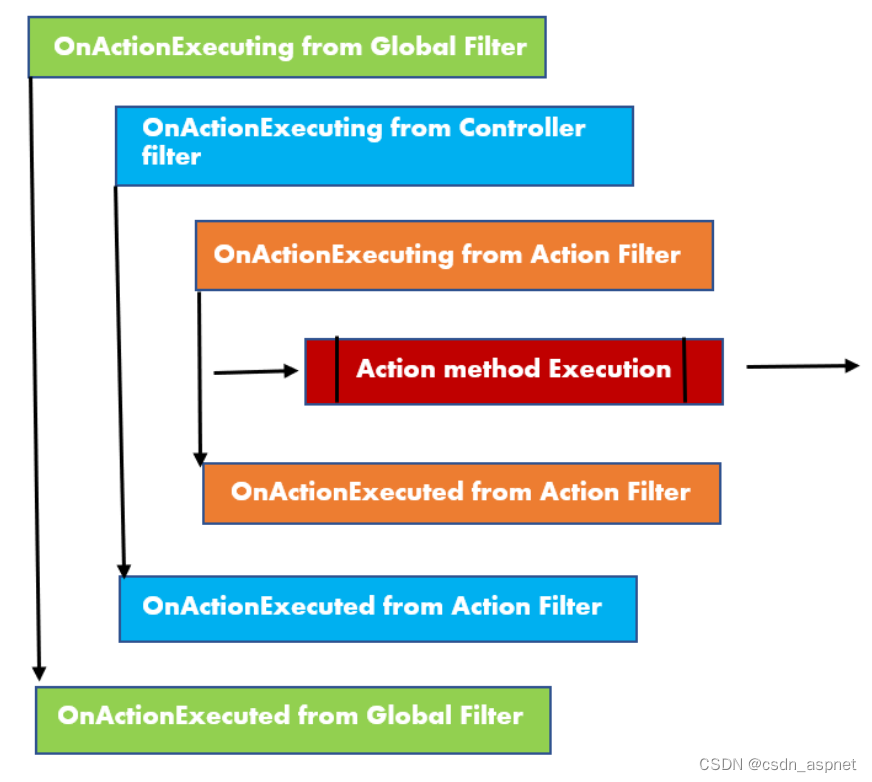
ASP.NET Core 过滤器 使用依赖项注入
过滤器是 ASP.NET Core 中的特殊组件,允许我们在请求管道的特定阶段控制请求的执行。这些过滤器在中间件执行后以及 MVC 中间件匹配路由并调用特定操作时发挥作用。 简而言之,过滤器提供了一种在操作级别自定义应用程序行为的方法。它们就像检查点&#…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

