阿赵的MaxScript学习笔记分享十二《获取和导出各种数据》
大家好,我是阿赵,周日的早上继续分享MaxScript学习笔记,这是第十二篇,获取和导出各种数据
1、导出数据的目的
使用3DsMax建立3D模型后,很多时候需要输出模型到别的引擎去使用,常用的格式有Obj、FBX、SLT等。有时候,这些通用的格式里面的数据不够,比如obj里面就没有带顶点颜色。有时候是因为某些格式的解析比较复杂,比如FBX,之类,我们会需要根据自己的需要来导出各种的数据。
一般来说,导出模型数据会包括以下这些:
顶点坐标
UV
UV2
顶点颜色
顶点法线
面的索引信息
蒙皮信息
材质贴图
动画关键帧
等
首先要明白一个概念,比如一个box,他是由8个顶点、6个四角面组成的。但在导出到引擎使用的时候,其实他是24个点,12个面的,因为游戏引擎绘制的一般是三角面,所以一个四角面会拆分成2个三角面。然后从UV和法线的角度,同一个顶点,有可能是被多个面同时使用的,所以顶点在属于不同的面的时候,顶点的UV坐标和法线方向也是不一样的。
所以,在导出数据的时候,可以使用自己的方式去处理数据。其中一个方法是可以参数obj格式,他把重复的顶点、UV坐标、法线方向进行合并,每个数据有一个索引index,然后在记录面数据的时候,比如一个box有12个面,他会记录12个面的信息,每个面有3个顶点,每个顶点包含了顶点索引、法线索引和uv索引的数据。这样操作下来,存储的数据量最少,也不会丢失任何数据。当然如果想把顶点颜色的数据也加进去,也可以再增加一个顶点颜色的索引,把它带在面的顶点数据里面导出。
下面还是以一个box为思考的参考,列出了获取各种信息的方法,结合着之前讲过的字符串操作方法,和文件读写方法,就可以根据自己的需要取导出自己的模型格式了
2、各种数据的获取方式举例
--获得网格顶点数
GetNumVerts boxt1.mesh
8
--获得某个通道的顶点数据数量,1通道代表UV通道,
--这里我能用1通道,是因为我已经展过UV了,如果没有展过UV,会报错
polyop.getNumMapVerts boxt1 1
24
--获得实际的三角面数
GetNumFaces boxt1.mesh
12
--获得第一个顶点的坐标
getVert boxt1.mesh 1
[-12.5,-12.5,0]
--获得第12个面使用了哪几个顶点,对应网格顶点数的索引
getface boxt1.mesh 12
[3,1,5]
--获得第12个面的法线方向
GetFaceNormal boxt1.mesh 12
[-1,0,0]
--获得第12个面引用的UV索引,对应UV坐标索引
GetTVFace boxt1.mesh 12
[9,10,11]
--获得第9个UV索引点的UV坐标
getTVert boxt1.mesh 9
[0.0005,0.0005,0]
特别说一下法线的获取方式和设置方式
法线的获取和赋值比较特殊一点,需要注意以下几点:
1.如果不通过Edit_Normals修改器来获取,法线的数据是不正确的
box02 = box()
$Box:Box003 @ [0.000000,0.000000,0.000000]converttopoly box02
$Editable_Poly:Box003 @ [0.000000,0.000000,0.000000]faceNum = polyop.getnumfaces box02
6
for i in 1 to faceNum do
(
local faceNormal = polyop.getfacenormal box02 i
print faceNormal
)
[0,0,-1]
[0,0,1]
[0,-1,0]
[1,0,0]
[0,1,0]
[-1,0,0]
OKvertNum = box02.numverts
8
for i in 1 to vertNum do
(local vertNormal = getNormal box02.mesh iprint vertNormal
)
[0,0,-1.5708]
[0,0,-1.5708]
[0,0,-1.5708]
[0,0,-1.5708]
[0,0,1.5708]
[0,0,1.5708]
[0,0,1.5708]
[0,0,1.5708]
OK
通过以上的代码,似乎可以通过polyop来获取某个面的法线方向,然后也可以用点的index通过getNormal的方法来获取到mesh里面某个点的法线方向。
但其实这个获取的方法是有问题的
(1)首先来说这个面的法线,这个面的发现方向,从一个box的4个面的角度看,是正确的,但如果我们通过添加Edit_Normals编辑器,修改其中一个面的法线,然后再次打印6个面的法线方向,会发现结果根本没有变化。所以我个人感觉,这个从polyop里面获取的面法线方向,并不是通过4个顶点的法线方向计算出来的值,只是通过4个顶点的坐标位置,算出来的一个法线方向。如果在不修改顶点法线的情况下,应该是可以用的,但我们谈论的获取法线方向,一般是指顶点的法线方向,所以这个面的法线方向其实没什么意义
(2)再来看通过getNormal方法获得的顶点法线,会发现这个值有点莫名其妙,首先,8个点只有2种法线方向,然后,这个法线也没有归一化,长度并不是1的,所以这个获取的结果,我觉得也是并没有什么用途的。实际上,一个顶点有可能不止一个法线方向的,下面会继续分析。
2.一个顶点具体包含多少个法线,要看具体的平滑组设置

box03 = box()
$Box:Box003 @ [0.000000,0.000000,0.000000]
converttopoly box03
$Editable_Poly:Box003 @ [0.000000,0.000000,0.000000]
select box03
OK
modPanel.addModToSelection (Edit_Normals()) ui:on
OK
通过一段代码,创建一个box,然后添加了一个Edit_Normals的修改器,这时候我们可以看到场景里面的box每个顶点上面伸出了3条线,这些线,其实就是法线了。由于一个box有8个顶点,所以这个时候,应该有24条法线。
为什么会有24条这么多呢?那是因为这个box每个面的光滑组都不一样,所以面与面之间,是硬转角,而虽然我们看来这个box只有8个顶点,但每个顶点同时被3个面共用,所以一个顶点需要3个法线方向来分别代表组成不同面时,该顶点的法线方向。

这时候,做一下修改,返回Editable Poly,选择所有面,把它们的光滑组都改成1

再回到Edit_Normals,这时候,可以看到每个顶点只有1根法线了。这究竟是真的一个顶点变成1根法线,还是由于同一个顶点的法线都重叠在一起了呢?我们可以通过代码去验证一下。
local myVerts = #{1,2,3,4,5,6,7,8}
local myNormals = #{}
local modN = box03.modifiers[1]
modN.ConvertVertexSelection &myVerts&myNormals
print myNormals
这里有一段代码,由于现在box03的第一个修改器就是Edit_Normals,所以modN获取了这个Edit_Normals修改器,然后通过ConvertVertexSelection ,获取指定的myVerts的8个顶点使用到的法线id到myNormals数组
当把box03的光滑组取消的时候,得到的打印结果是:
#{1…24}
当把box03的所有面光滑组设置成1后,得到的打印结果是:
#{1…8}
很明显,在把所有面的光滑组设置成1后,这个box03的法线方向的确是只剩下了8个。于是我们能得出结论,模型的一个顶点具体有多少个法线方向,是根据面的光滑组来分的。或者换个说法,面与面之间是硬边过渡,还是光滑过渡,是看组成面之间的边缘的顶点,是否共用法线。
3.通过Edit_Normals修改器来获取法线数据
通过了上面的实验,我们知道,只有通过Edit_Normals修改器,才能比较准确的获得和修改模型的法线。所以接下来就使用这个修改器来获取数据。
具体的步骤是这样的?
(1)通过ConvertVertexSelection 方法,获取到所有的NormalId
(2)通过GetFaceDegree方法逐个面获取当前的面有多少个不同角度的点组成
(3)通过GetNormalID方法,获得组成每个面每个顶点的对应NormalId
(4)根据1和4的结果,就可以知道每个顶点的发现方向了
具体代码:
local vertNum = box03.numVertslocal myVerts = #{1..vertNum}local myNormals = #{}local modN = box03.modifiers[1]--通过ConvertVertexSelection把所有顶点用到的normalId存到myNormals数组modN.ConvertVertexSelection &myVerts&myNormals--通过GetNormal方法把每一个normalId对应的法线方向,存到normalArr里面local normalArr = #()for i in myNormals do(local norPos = modN.GetNormal inormalArr[i] = norPos)print "法线集合:"print normalArr--获得面的数量local faceNum = modN.GetNumFaces()local faceNormalIdList = #()for i in 1 to faceNum do(--corner的含义可以理解成这个面由多少个不同角度的点组成local corners = modN.GetFaceDegree i--遍历组成面的这些conner,通过GetNormalID方法,获得组成这个面的顶点对应的normalIdlocal tempFaceNormalList = #()for j in 1 to corners do(local norInd = modN.GetNormalID i jappend tempFaceNormalList norInd)faceNormalIdList[i] = tempFaceNormalList) print "面对应法线Id"print faceNormalIdList
运行的结果:
"法线集合:"
[0,0,-1]
[0,0,-1]
[0,0,-1]
[0,0,-1]
[0,0,1]
[0,0,1]
[0,0,1]
[0,0,1]
[0,-1,0]
[0,-1,0]
[0,-1,0]
[0,-1,0]
[1,0,0]
[1,0,0]
[1,0,0]
[1,0,0]
[0,1,0]
[0,1,0]
[0,1,0]
[0,1,0]
[-1,0,0]
[-1,0,0]
[-1,0,0]
[-1,0,0]
"面对应法线Id"
#(1, 2, 3, 4)
#(5, 6, 7, 8)
#(9, 10, 11, 12)
#(13, 14, 15, 16)
#(17, 18, 19, 20)
#(21, 22, 23, 24)
根据需要,把这些数据保存你的文件里面就可以了。
4.修改法线
顺便提一下怎样修改法线。
之前用GetNormalId可以获取到某个点的NormalId,然后用GetNormal可以获得对应NormalId的具体法线方向值。那么反过来,通过SetNormal方法,就可以改变对应NormalId的点的法线方向了,比如,刚才那个例子,需要把第16个NormalId的值改成[0.5,0.6,0.7],可以这样:
modN.SetNormal 16 [0.5,0.6,0.7]
相关文章:

阿赵的MaxScript学习笔记分享十二《获取和导出各种数据》
大家好,我是阿赵,周日的早上继续分享MaxScript学习笔记,这是第十二篇,获取和导出各种数据 1、导出数据的目的 使用3DsMax建立3D模型后,很多时候需要输出模型到别的引擎去使用,常用的格式有Obj、FBX、SLT等…...

react-draggable实现拖拽详解
react-draggable属性常用属性属性列表事件列表举例首先安装 react-draggable实现移动希望小编写的能够帮助到你😘属性 常用属性 属性默认值介绍axisxhandle拖动的方向,可选值 x ,y,bothhandle无指定拖动handle的classposition无handle的位置࿰…...

01.进程和线程的区别
进程和线程的区别进程和线程是计算机中的两个核心概念,它们都是用来实现并发执行的方式,但是它们在实现并发的方式和资源管理方面有一些重要的区别。进程是一个程序的运行实例。每个进程都有自己的内存空间、代码、数据和系统资源(如文件描述…...

逻辑优化-rewrite
简介 逻辑综合中的rewrite算法是一种常见的优化算法,其主要作用是通过对逻辑电路的布尔函数进行等效变换,从而达到优化电路面积、时序和功耗等目的。本文将对rewrite算法进行详细介绍,并附带Verilog代码示例。 一、算法原理 rewrite算法的…...
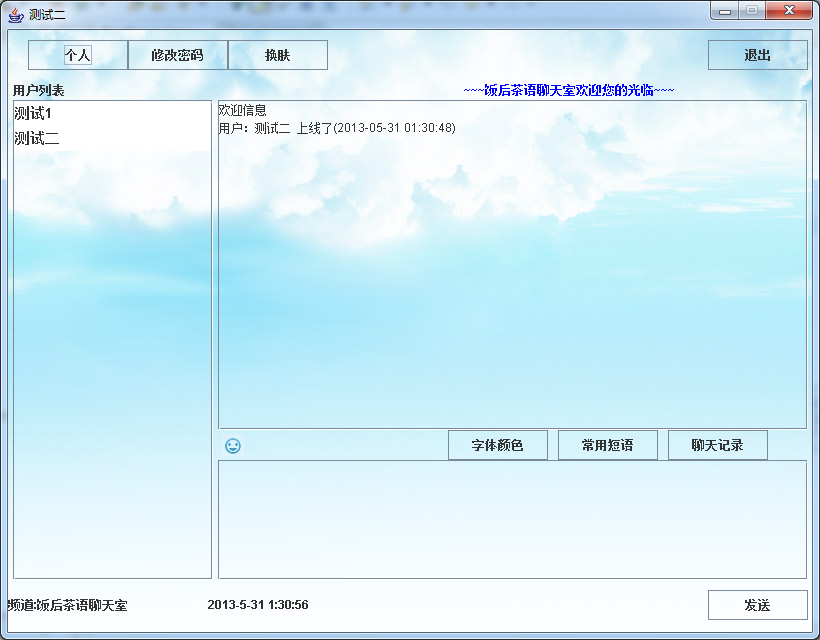
文件传输与聊天系统设计
技术:Java等摘要:本文介绍了一种基于TCP/IP协议使用Socket技术实现的聊天室系统,包括私聊功能和文件传输功能,对系统的主要模块进行了分析,并对系统实现过程中遇到的关键性技术进行了阐述,最后对系统进行了…...
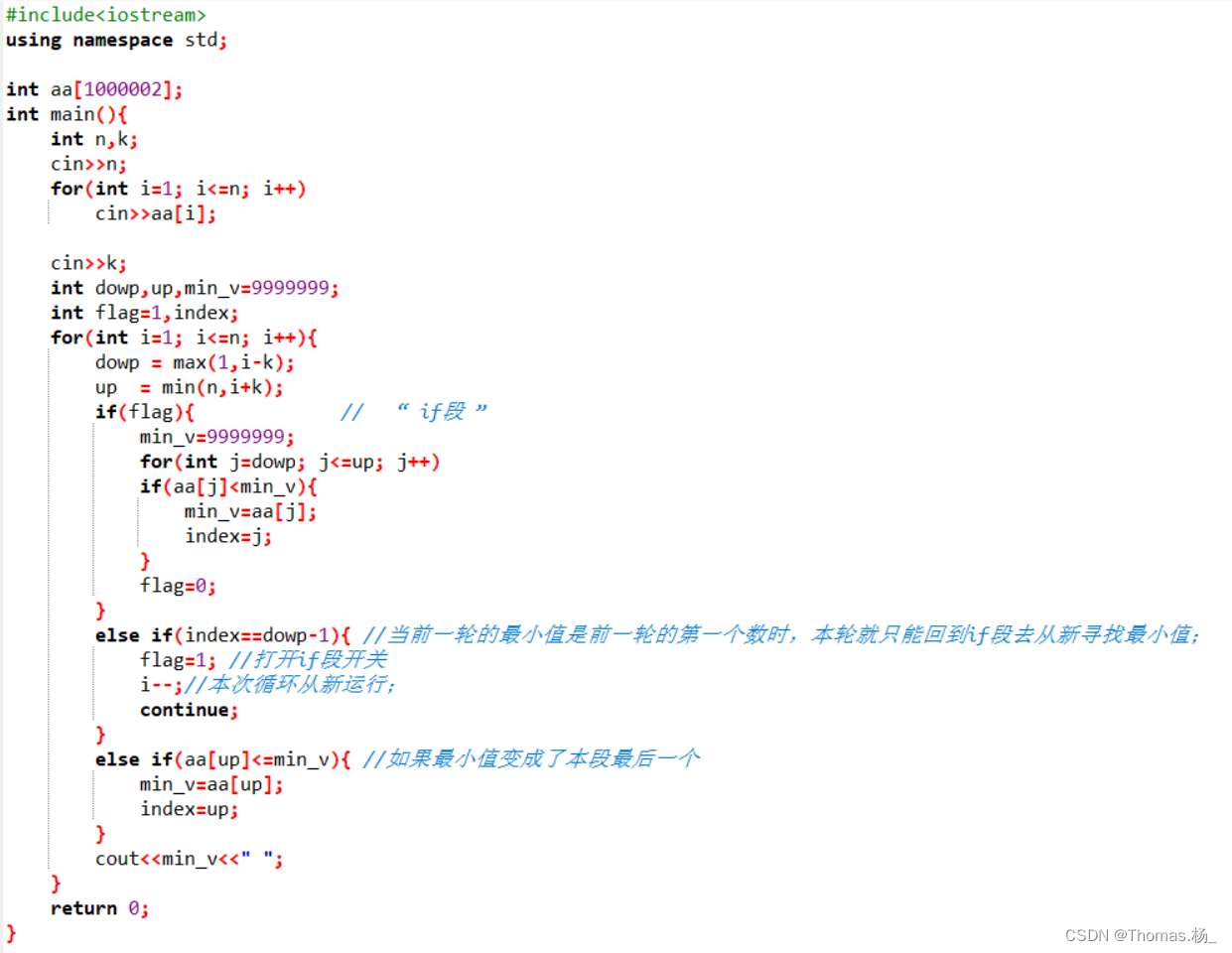
蓝桥杯第十四届校内赛(第三期) C/C++ B组
一、填空题 (一)最小的十六进制 问题描述 请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。 请将这个数的十进制形式作…...

有关平方或高次方的公式整理一元高次方程的求解
Part.I Introduction 这篇博文记录一下数学中常用的有关平方或高次方的一些公式。 Chap.I 一些结论 下面一部分汇总了一些重要的结论 完全平方公式:(ab)2a22abb2(ab)^2a^22abb^2(ab)2a22abb2平方差公式:a2−b2(ab)(a−b)a^2-b^2(ab)(a-b)a2−b2(ab)(…...

Java笔记3
ArrayListArrayList<String> list new Arraylist<>();<>是泛型表示存放的数据类型,注意不能是基本数据类型;增删改查增:add 返回值为true删:remove 1.直接删元素2.根据索引删元素改:set(…...

Leetcode.2202 K 次操作后最大化顶端元素
题目链接 Leetcode.2202 K 次操作后最大化顶端元素 Rating : 1717 题目描述 给你一个下标从 0开始的整数数组 nums,它表示一个 栈 ,其中 nums[0]是栈顶的元素。 每一次操作中,你可以执行以下操作 之一 : 如果栈非空…...

JAVA知识点全面总结3:String类的学习
三.String类学习 1.String,StringBuffer,StringBuilder的区别? 2.字符串拼接用加号的原理 ? 3.字符串常量池如何理解? 4.String的intern方法理解? 5.String的equals方法和compareTo方法的使用…...
Eureka注册中心和Nacos注册中心详解以及Nacos与Eureka有什么区别?
目录:前言Eureka注册中心Nacos注册中心Nacos与Eureka有什么区别?前言提供接口给其它微服务调用的微服务叫做服务提供者,而调用其它微服务提供的接口的微服务则是服务消费者。如果服务A调用了服务B,而服务B又调用了服务C࿰…...

Web3D发展趋势以及Web3D应用场景
1,Web3D发展趋势随着互联网的快速发展,Web3D技术也日渐成熟,未来发展趋势也值得关注。以下是Web3D未来发展趋势的七个方面:可视化和可交互性的增强:Web3D可以为三维数据提供可视化和可交互性的增强,将极大地…...

2023-3-4 刷题情况
按位与为零的三元组 题目描述 给你一个整数数组 nums ,返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件: 0 < i < nums.length 0 < j < nums.length 0 < k < nums.l…...
前端面试总结
1.引言 最近参加了大量的招聘会,投递了大量的简历,整整体会了从“随便找个厂上一下”——“还是的找个大厂”——“没人要”——“急了急了,海投一波”——“工资有点尬”——“海投中…”。简单说一下自己的一些感受吧,现在的前端属实有点尴…...
: Spatial clustering)
Geospatial Data Science (6): Spatial clustering
Geospatial Data Science (6): Spatial clustering 1.Clustering, spatial clustering, and geodemographics 本节涉及空间观测的统计聚类。许多问题和主题都是复杂的现象,涉及多个维度,难以归纳为一个单一的变量。在统计学术语中,我们把这一类问题称为多变量,而不是在…...

蚁群算法优化问题
%%%%%%%%%%%%蚁群算法解决 TSP 问题%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%% clear all; %清除所有变量 close all; %清图 clc; %清屏 m 50; %蚂蚁个数 Alpha 1; %信息素重要程度参数 Beta 5; %启发式因子重要程度参数 Rho 0.1; %信息素蒸发系数 G 20…...

为啥一个 main 方法就能启动项目
在 Spring Boot 出现之前,我们要运行一个 Java Web 应用,首先需要有一个 Web 容器(例如 Tomcat 或 Jetty),然后将我们的 Web 应用打包后放到容器的相应目录下,最后再启动容器。 在 IDE 中也需要对 Web 容器…...

洛谷:P1554 梦中的统计 JAVA
思路:定义一个长度为10的数组,数组下标代表数组元素的数字,比如arr[0]代表数字0.用一个for循环,对每个数先取余再取整,知道取整得到的数为0,说明该数字已经被拆解完了。今天又学了一个输入,原来…...
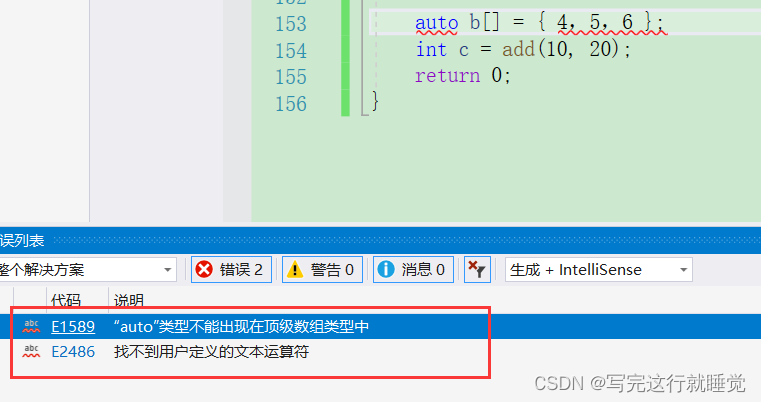
C++初学笔记整理
目录 1. C关键字 2. 命名空间 1)命名空间的引入和概述 2)命名空间的定义 3)std与命名空间的使用 4).相关特性 3. C输入&输出 4. 缺省参数 1 )缺省参数概念 2)使用及分类 a.全缺省 b.部分缺省 5. 函数…...

记录--在Vue3这样子写页面更快更高效
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 前言 在开发管理后台过程中,一定会遇到不少了增删改查页面,而这些页面的逻辑大多都是相同的,如获取列表数据,分页,筛选功能这些基本功能。而…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
