【算法与数据结构】198、213、337LeetCode打家劫舍I, II, III
文章目录
- 一、198、打家劫舍
- 二、213、打家劫舍 II
- 三、337、打家劫舍III
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、198、打家劫舍

思路分析:打家劫舍是动态规划的的经典题目。本题的难点在于递归公式和初始化。
- 第一步, d p [ j ] dp[j] dp[j]的含义。 d p [ j ] dp[j] dp[j]代表到第 j j j家的时候,偷窃到的最高金额。
- 第二步,递推公式。 d p [ j ] dp[j] dp[j]仅仅与 d p [ j − 1 ] dp[j-1] dp[j−1]和 d p [ j − 2 ] dp[j-2] dp[j−2]有关。如果不偷第 j j j家,则偷窃金额不变, d p [ j ] = d p [ j − 1 ] dp[j] = dp[j-1] dp[j]=dp[j−1]。如果偷第 j j j家,那么偷窃金额在 d p [ j − 2 ] dp[j-2] dp[j−2]基础上加上 n u m s [ i ] nums[i] nums[i],即 d p [ j ] = d p [ j − 2 ] + n u m s [ i ] dp[j] = dp[j-2] + nums[i] dp[j]=dp[j−2]+nums[i]。综合二者, d p [ j ] = m a x ( d p [ j − 1 ] , d p [ j − 2 ] + n u m s [ i ] ) dp[j] = max(dp[j-1], dp[j-2] + nums[i]) dp[j]=max(dp[j−1],dp[j−2]+nums[i])。
- 第三部,元素初始化。 d p [ 0 ] dp[0] dp[0]初始化为0,代表还没开始偷窃; d p [ 1 ] dp[1] dp[1]初始化为 n u m [ 0 ] num[0] num[0]。
- 第四部,递归顺序。循环从 j = 2 j = 2 j=2开始。
- 第五步,打印结果。
程序如下:
// 198、打家劫舍,动态规划
class Solution {
public:int rob(vector<int>& nums) {vector<int> dp(nums.size() + 1, 0);dp[1] = nums[0];for (int i = 2; i <= nums.size(); i++) {dp[i] = max(dp[i - 1], dp[i - 2] + nums[i-1]);}return dp[nums.size()];}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( n ) O(n) O(n)。
因为只用到了dp数组的最后一个元素,实际上不需要保存所有的元素。因此对上述代码进行内存优化,将空间复杂度降低到 O ( 1 ) O(1) O(1),但是递归的过程不明显,找bug费劲。
// 198、打家劫舍,动态规划-内存优化
class Solution2 {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];int first = nums[0], second = max(nums[0], nums[1]);for (int i = 2; i < nums.size(); i++) {int temp = second;second = max(second, first + nums[i]);first = temp;}return second;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
二、213、打家劫舍 II
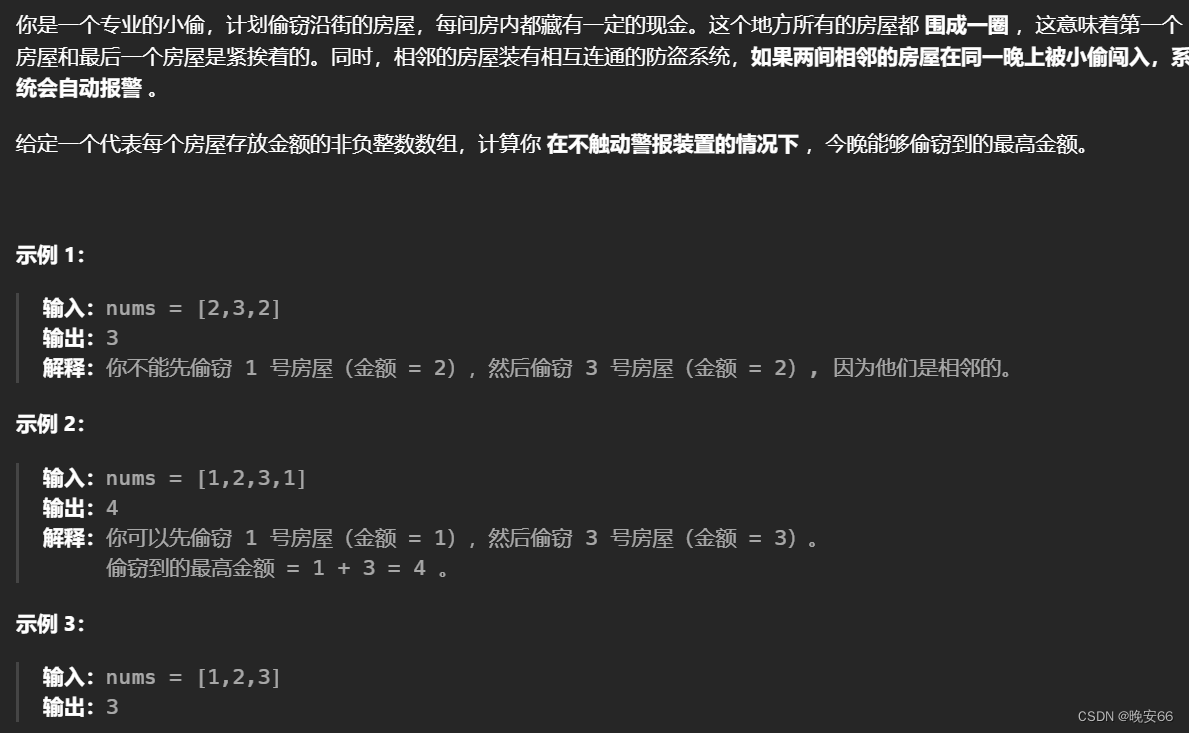
思路分析:本题是打家劫舍I的升级版,要求第一家和最后一家是连着的,不能同时偷。这是一个非此即彼的问题。要么偷第一家,不偷最后一家,这等于将最后一家排除在外。反之,不偷第一家,偷最后一家,等价于将第一家排除在外。假设第一家的下标为 0 0 0,最后一家的下标为 i − 1 i-1 i−1,那么一共有两种情况:偷窃范围 [ 0 , i − 2 ] [0, i - 2] [0,i−2],偷窃范围 [ 1 , i − 1 ] [1, i - 1] [1,i−1]。然后应用打家劫舍I的思路来做即可。以下是动态规划的代码,内存优化版本就没给出了,思路都是一样的。
程序如下:
// 213、打家劫舍II,动态规划
class Solution3 {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];int result1 = robRange(nums, 0, nums.size() - 2);int result2 = robRange(nums, 1, nums.size() - 1);return max(result1, result2);}int robRange(vector<int>& nums, int start, int end) {if (end == start) return nums[start];vector<int> dp(nums.size(), 0);dp[start] = nums[start];dp[start + 1] = max(nums[start], nums[start + 1]);for (int i = start + 2; i <= end; i++) {dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);}return dp[end];}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( n ) O(n) O(n)。
三、337、打家劫舍III
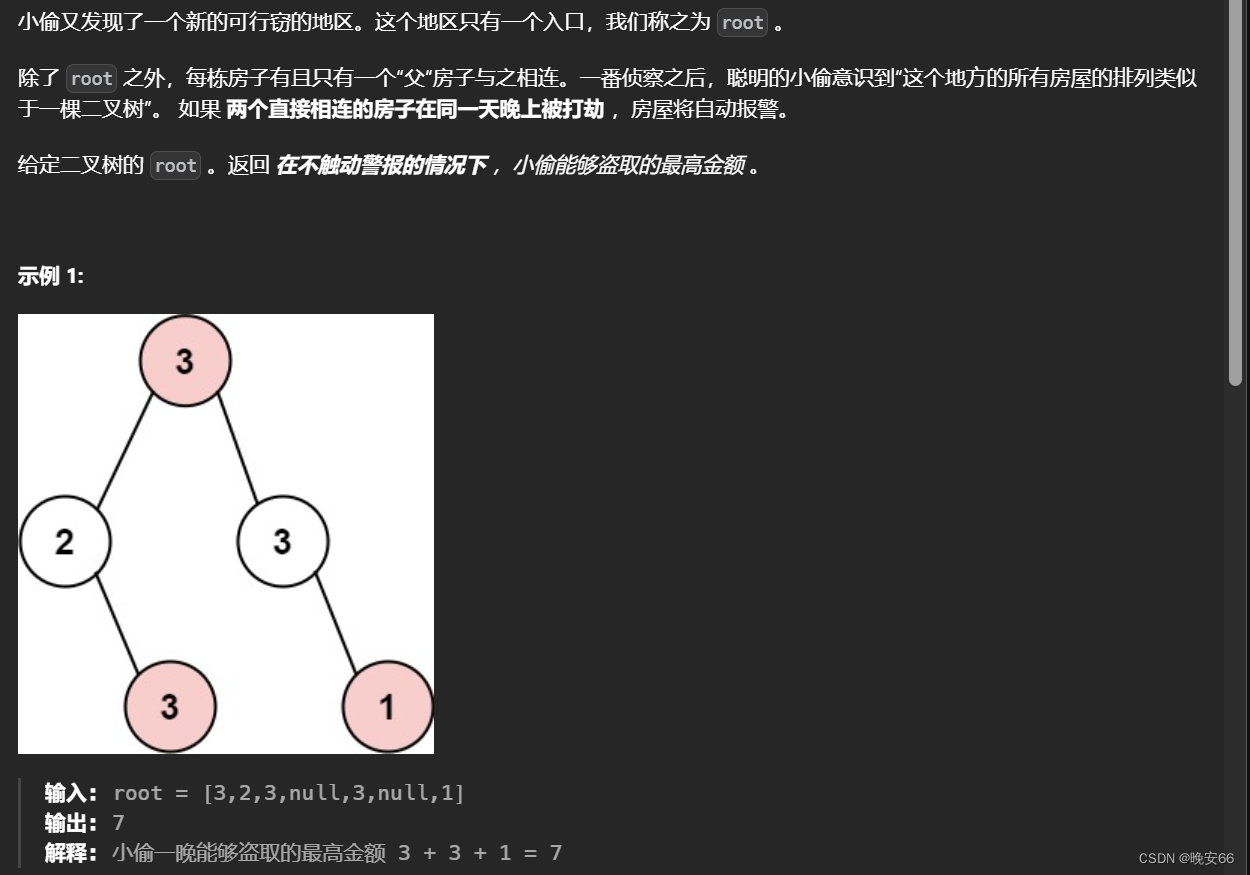
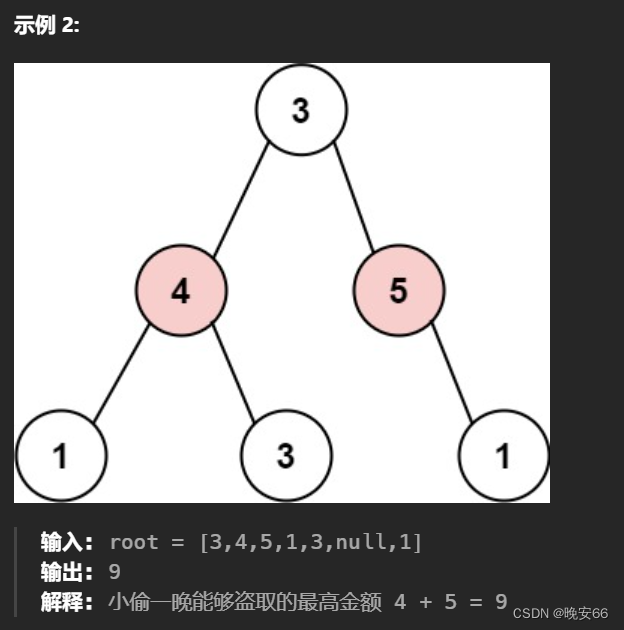
思路分析:本题是打家劫舍I的变体,原题目中的数组变成了二叉树。本题涉及到树形递归和动态规划,我们就结合递归三部曲和动态规划五步骤:
- 1、返回值和递归参数。我们需要判断一个节点要不要偷,而偷不偷取决于动作带来的收益。因此,我们需要返回一个节点偷与不偷的两个状态所得的金额。这就是一个长度为2的数组。这里我们假设这个二维数组第一个元素代表不偷的收益,第二个元素代表偷的收益,{ 0 , 1 = 不偷的收益,偷的收益 {0, 1} = {不偷的收益,偷的收益} 0,1=不偷的收益,偷的收益}。输入参数是当前节点。
- 2、确定终止条件。当遇到空节点就返回,空节点不会带来收益。因此返{ 0 , 0 {0,0} 0,0}。
if (cur == NULL) return vector<int>{0, 0};
- 3、确定遍历顺序。因为当前节点偷不偷需要根据左右孩子的返回值来进行判断,所以 我们需要先得到左右孩子的返回值,即先遍历左右孩子。在所有的遍历顺序中,只有后序遍历(左右中遍历顺序)满足。
vector<int> left = robTree(cur->left); // 左vector<int> right = robTree(cur->right); // 右
- 4、确定单层递归逻辑。对于当前节点来说,只有两个情况。如果偷当前节点,那么左右孩子节点就不能偷,偷的收益=左孩子不偷的收益+右孩子不偷的收益。如果不偷当前节点,那么左右孩子节点可偷可不偷,至于究竟偷不偷就看那个收益大(注意偷的收益未必更大,偷了小的金额,旁边大的金额就偷不了)。不偷的收益 = max(左孩子不偷的收益,左孩子偷的收益)+max(右孩子不偷的收益,右孩子偷的收益)。将文字抽象成公式:
int val1 = cur->val + left[0] + right[0]; // 偷当前节点,那么左右孩子节点不能偷int val2 = max(left[0], left[1]) + max(right[0], right[1]); // 不偷当前节点,那么左右孩子节点可以偷也可以不偷,取决于偷或者是不偷的金额。
- 5、具体示例推导dp数组,验证。
程序如下:
// 337、打家劫舍III动态规划
class Solution {
public:int rob(TreeNode* root) {vector<int> result = robTree(root);return max(result[0], result[1]);}vector<int> robTree(TreeNode* cur) { // 返回一个二维数组, {0, 1} = {不偷的金额,偷的金额}if (cur == NULL) return vector<int>{0, 0};vector<int> left = robTree(cur->left);vector<int> right = robTree(cur->right);int val1 = cur->val + left[0] + right[0]; // 偷当前节点,那么左右孩子节点不能偷int val2 = max(left[0], left[1]) + max(right[0], right[1]); // 不偷当前节点,那么左右孩子节点可以偷也可以不偷,取决于偷或者是不偷的金额。return { val2, val1 };}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),每个节点只遍历了一次。
- 空间复杂度: O ( l o g n ) O(log n) O(logn),算上递推系统栈的空间。
三、完整代码
// 打家劫舍I, II
# include <iostream>
# include <vector>
# include <algorithm>
using namespace std;// 198、打家劫舍,动态规划
class Solution {
public:int rob(vector<int>& nums) {vector<int> dp(nums.size() + 1, 0);dp[1] = nums[0];for (int i = 2; i <= nums.size(); i++) {dp[i] = max(dp[i - 1], dp[i - 2] + nums[i-1]);}return dp[nums.size()];}
};// 198、打家劫舍,动态规划-内存优化
class Solution2 {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];int first = nums[0], second = max(nums[0], nums[1]);for (int i = 2; i < nums.size(); i++) {int temp = second;second = max(second, first + nums[i]);first = temp;}return second;}
};// 213、打家劫舍II,动态规划
class Solution3 {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];int result1 = robRange(nums, 0, nums.size() - 2);int result2 = robRange(nums, 1, nums.size() - 1);return max(result1, result2);}int robRange(vector<int>& nums, int start, int end) {if (end == start) return nums[start];vector<int> dp(nums.size(), 0);dp[start] = nums[start];dp[start + 1] = max(nums[start], nums[start + 1]);for (int i = start + 2; i <= end; i++) {dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);}return dp[end];}
};int main() {vector<int> nums = { 1,2,3,1 };Solution3 s1;int result = s1.rob(nums);cout << result << endl;system("pause");return 0;
}
// 337、打家劫舍III
# include <iostream>
# include <vector>
# include <string>
# include <queue>
using namespace std;// 树节点定义
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};template<typename T>
void my_print(T& v, const string msg)
{cout << msg << endl;for (class T::iterator it = v.begin(); it != v.end(); it++) {cout << *it << ' ';}cout << endl;
}template<class T1, class T2>
void my_print2(T1& v, const string str) {cout << str << endl;for (class T1::iterator vit = v.begin(); vit < v.end(); ++vit) {for (class T2::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {cout << *it << ' ';}cout << endl;}
}// 前序遍历迭代法创建二叉树,每次迭代将容器首元素弹出(弹出代码还可以再优化)
void Tree_Generator(vector<string>& t, TreeNode*& node) {if (!t.size() || t[0] == "NULL") return; // 退出条件else {node = new TreeNode(stoi(t[0].c_str())); // 中if (t.size()) {t.assign(t.begin() + 1, t.end());Tree_Generator(t, node->left); // 左}if (t.size()) {t.assign(t.begin() + 1, t.end());Tree_Generator(t, node->right); // 右}}
}// 层序遍历
vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size(); // size必须固定, que.size()是不断变化的vector<int> vec;for (int i = 0; i < size; ++i) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}return result;
}// 337、打家劫舍III动态规划
class Solution {
public:int rob(TreeNode* root) {vector<int> result = robTree(root);return max(result[0], result[1]);}vector<int> robTree(TreeNode* cur) { // 返回一个二维数组, {0, 1} = {不偷的金额,偷的金额}if (cur == NULL) return vector<int>{0, 0};vector<int> left = robTree(cur->left);vector<int> right = robTree(cur->right);int val1 = cur->val + left[0] + right[0]; // 偷当前节点,那么左右孩子节点不能偷int val2 = max(left[0], left[1]) + max(right[0], right[1]); // 不偷当前节点,那么左右孩子节点可以偷也可以不偷,取决于偷或者是不偷的金额。return { val2, val1 };}
};int main() {vector<string> t = { "3", "2", "NULL", "3", "NULL", "NULL", "3", "NULL", "1", "NULL", "NULL"}; // 前序遍历TreeNode* root = new TreeNode(); // 生成根节点Tree_Generator(t, root); // 生成树vector<vector<int>> tree = levelOrder(root); // 层序遍历my_print2<vector<vector<int>>, vector<int>>(tree, "目标树:"); // 打印层序遍历Solution s1;int result = s1.rob(root);cout << "最大金额为:" << result << endl;system("pause");return 0;
}
end
相关文章:

【算法与数据结构】198、213、337LeetCode打家劫舍I, II, III
文章目录 一、198、打家劫舍二、213、打家劫舍 II三、337、打家劫舍III三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、198、打家劫舍 思路分析:打家劫舍是动态规划的的经典题目。本题的难点在于递归公式…...

React、React Router、JSX 简单入门快速上手
React、React Router、JSX 简单入门快速上手 介绍特点 JSX使用js表达式渲染列表样式控制注意事项 入门脚手架创建react项目安装目录介绍入口文件解析 组件解析介绍函数式组件类组件 事件绑定注意点定义使用事件对象事件处理函数接收额外参数 组件状态状态的定义使用 组件通信父…...

从 0 开始搭建 React 框架
webpack 配置 不再赘述,可参考前三个文章(wenpack5 基本使用 1 - 3) 使用 react 安装 react、react-dom、babel/preset-react yarn add react react-dom babel/preset-react<!DOCTYPE html> <html lang"en"> <h…...

网站地址怎么改成HTTPS?
现在,所有类型的网站都需要通过 HTTPS 协议进行安全连接,而实现这一目标的唯一方法是使用 SSL 证书。如果您不将 HTTP 转换为 HTTPS,浏览器和应用程序会将您网站的连接标记为不安全。 但用户询问如何将我的网站从 HTTP 更改为 HTTPS。在此页…...
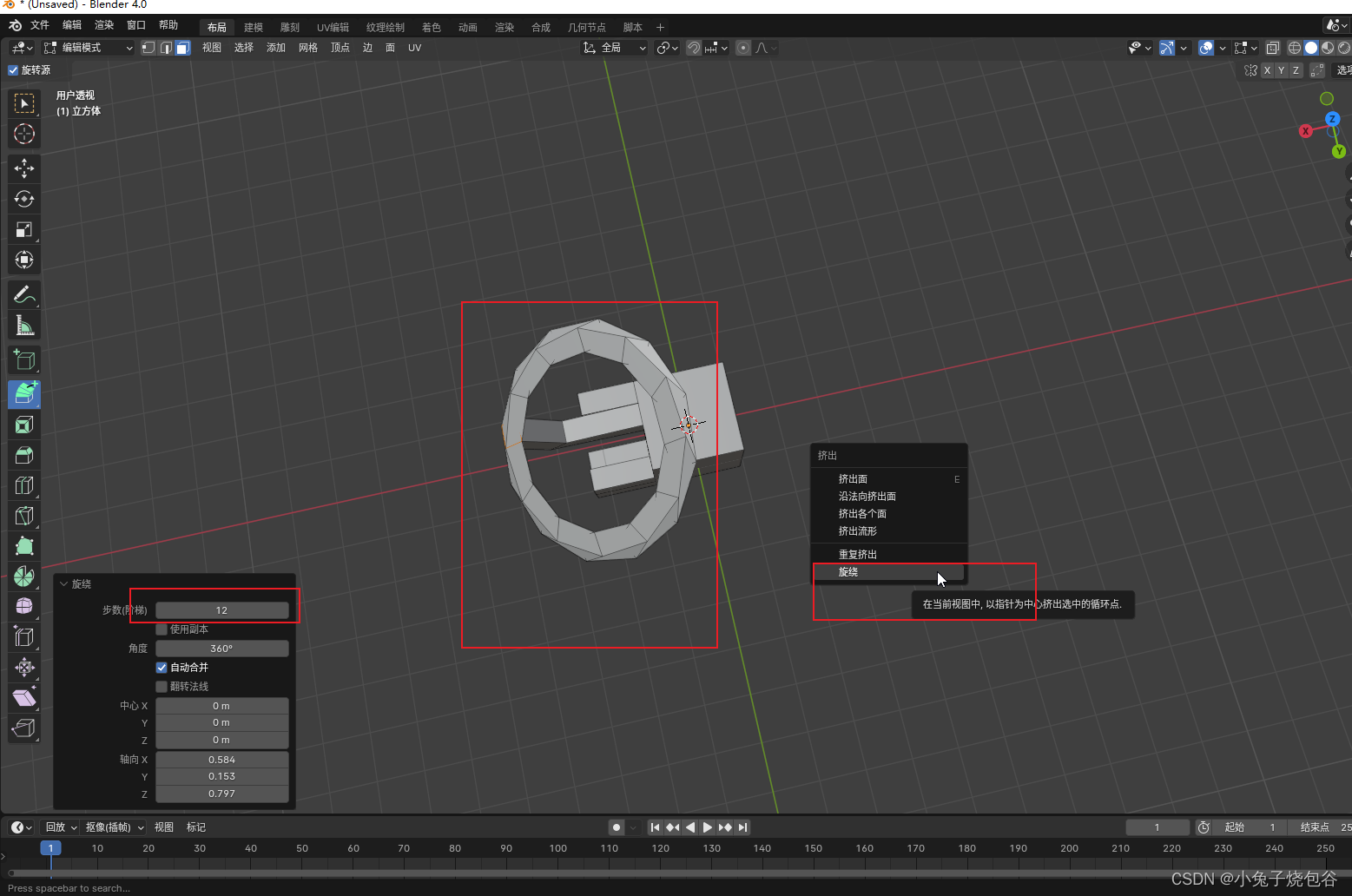
Blender教程(基础)-面的细分与删除、挤出选区-07
一、Blender之面的细分 新建一个立方体,在编辑模式下、选中一个面。 在选中的面上单击右键弹出细分选项,选择细分。 在选中细分后、会默认细分1次。修改细分次数在左下角 二、Blender之面的删除 选择中需要操作的面,在英文状态下按X键弹…...

QT自制软键盘 最完美、最简单、支持中文输入(二)
目录 一、前言 二、本自制虚拟键盘特点 三、中文输入原理 四、组合键输入 五、键盘事件模拟 六、界面 七、代码 7.1 frmKeyBoard 头文件代码 7.2 frmKeyBoard 源文件代码 八、使用示例 九、效果 十、结语 一、前言 由于系统自带虚拟键盘不一定好用,也不一…...

SpringCloud_学习笔记_1
SpringCloud01 1.认识微服务 随着互联网行业的发展,对服务的要求也越来越高,服务架构也从单体架构逐渐演变为现在流行的微服务架构。这些架构之间有怎样的差别呢? 1.0.学习目标 了解微服务架构的优缺点 1.1.单体架构 单体架构ÿ…...

容器算法迭代器初识
#include<iostream> using namespace std; #include<vector> //vetor容器存放内置数据类型 void test01() {//创建了一个vector容器,数组 vector<int> v;//向容器中插入数据v.push_back (10);//尾插 v.push_back (20);v.push_back (30);v.push_ba…...

瑞_力扣LeetCode_二叉搜索树相关题
文章目录 说明题目 450. 删除二叉搜索树中的节点题解递归实现 题目 701. 二叉搜索树中的插入操作题解递归实现 题目 700. 二叉搜索树中的搜索题解递归实现 题目 98. 验证二叉搜索树题解中序遍历非递归实现中序遍历递归实现上下限递归 题目 938. 二叉搜索树的范围和题解中序遍历…...

python爬虫爬取网站
流程: 1.指定url(获取网页的内容) 爬虫会向指定的URL发送HTTP请求,获取网页的HTML代码,然后解析HTML代码,提取出需要的信息,如文本、图片、链接等。爬虫请求URL的过程中,还可以设置请求头、请求参数、请求…...
c# Get方式调用WebAPI,WebService等接口
/// <summary> /// 利用WebRequest/WebResponse进行WebService调用的类 /// </summary> public class WebServiceHelper {//<webServices>// <protocols>// <add name"HttpGet"/>// <add name"HttpPost"/>// …...

银行数据仓库体系实践(11)--数据仓库开发管理系统及开发流程
数据仓库管理着整个银行或公司的数据,数据结构复杂,数据量庞大,任何一个数据字段的变化或错误都会引起数据错误,影响数据应用,同时业务的发展也带来系统不断升级,数据需求的不断增加,数据仓库需…...

微信小程序引导用户打开定位授权通用模版
在需要使用位置信息的页面(例如 onLoad 或 onShow 生命周期函数)中调用 wx.getSetting 方法检查用户是否已经授权地理位置权限: Page({onLoad: function() {wx.getSetting({success: res > {if (res.authSetting[scope.userLocation]) {/…...

JVM篇----第十篇
系列文章目录 文章目录 系列文章目录前言一、JAVA 强引用二、JAVA软引用三、JAVA弱引用四、JAVA虚引用五、分代收集算法前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给你的码吧…...
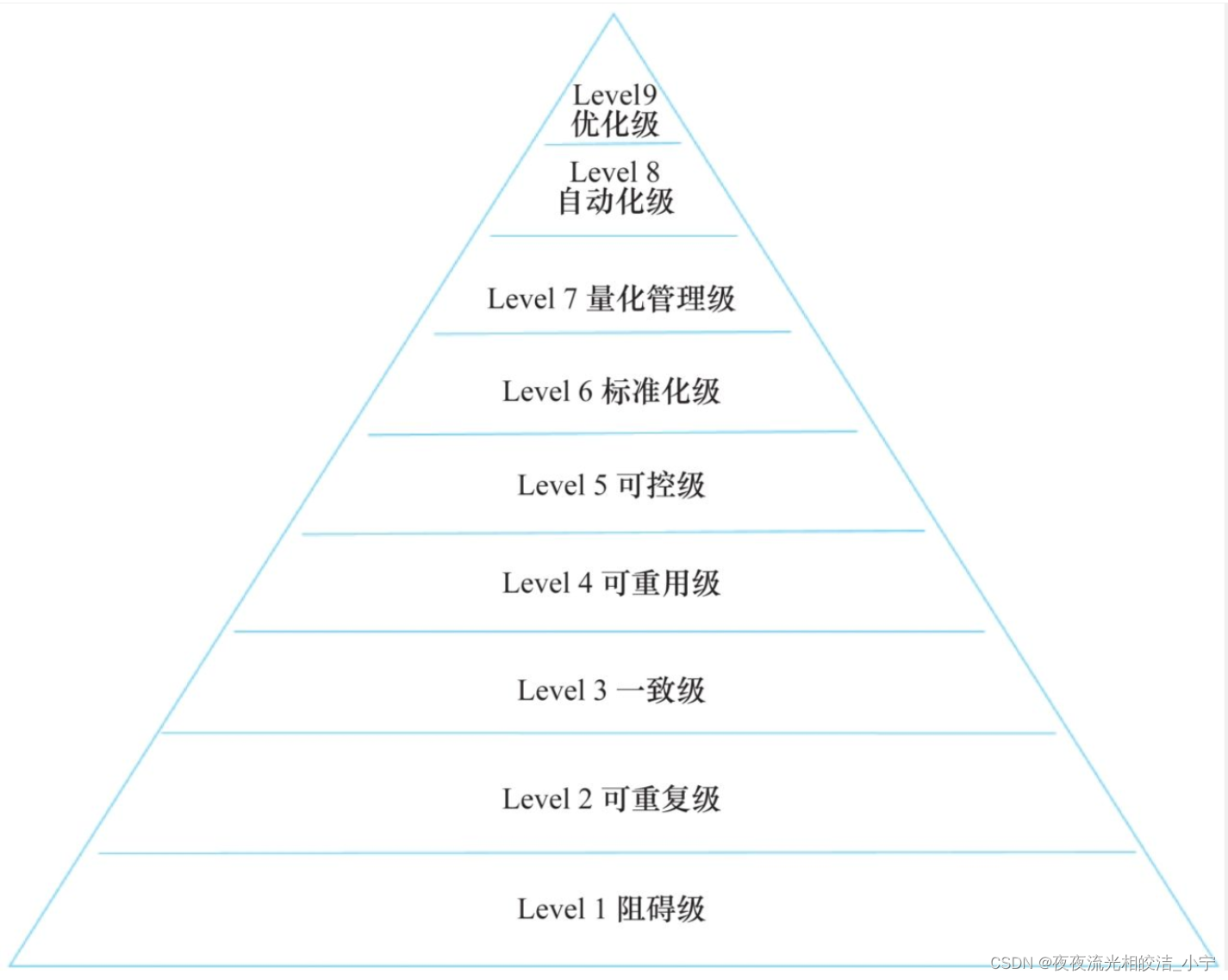
DevSecOps 参考模型介绍
目录 一、参考模型概述 1.1 概述 二、参考模型分类 2.1 DevOps 组织型模型 2.1.1 DevOps 关键特性 2.1.1.1 模型特性图 2.1.1.2 特性讲解 2.1.1.2.1 自动化 2.1.1.2.2 多边协作 2.1.1.2.3 持续集成 2.1.1.2.4 配置管理 2.1.2 DevOps 生命周期 2.1.2.1 研发过程划分…...

什么是okhttp?
OkHttp简介: OkHttp 是一个开源的、高效的 HTTP 客户端库,由 Square 公司开发和维护。它为 Android 和 Java 应用程序提供了简单、强大、灵活的 HTTP 请求和响应的处理方式。OkHttp 的设计目标是使网络请求变得更加简单、快速、高效,并且支持…...
R语言基础学习-02 (此语言用途小众 用于数学 生物领域 基因分析)
变量 R 语言的有效的变量名称由字母,数字以及点号 . 或下划线 _ 组成。 变量名称以字母或点开头。 变量名是否正确原因var_name2.正确字符开头,并由字母、数字、下划线和点号组成var_name%错误% 是非法字符2var_name错误不能数字开头 .var_name, var.…...
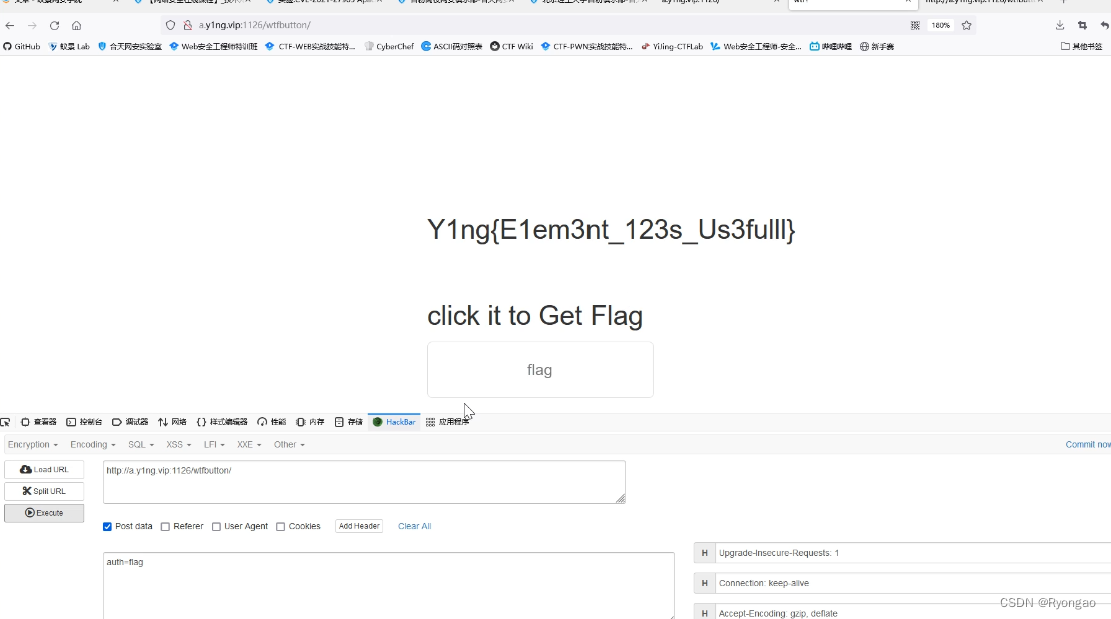
CTF-WEB的入门真题讲解
EzLogin 第一眼看到这个题目我想着用SQL注入 但是我们先看看具体的情况 我们随便输入admin和密码发现他提升密码不正确 我们查看源代码 发现有二个不一样的第一个是base64 意思I hava no sql 第二个可以看出来是16进制转化为weak通过发现是个弱口令 canyouaccess 如果…...
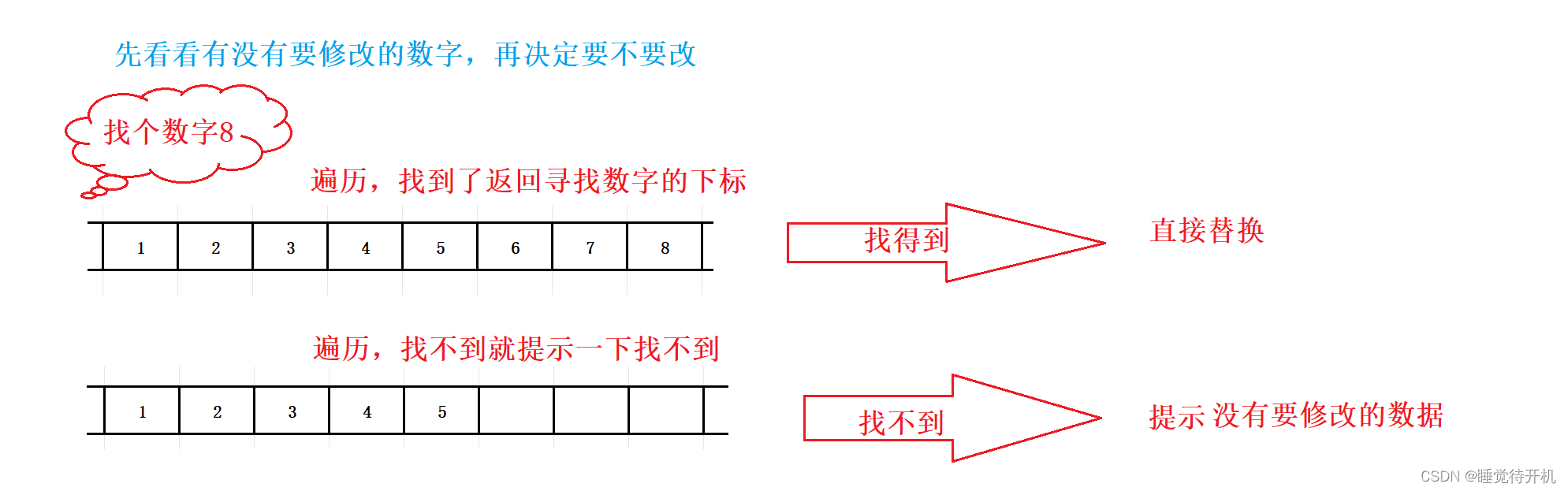
【C项目】顺序表
简介:本系列博客为C项目系列内容,通过代码来具体实现某个经典简单项目 适宜人群:已大体了解C语法同学 作者留言:本博客相关内容如需转载请注明出处,本人学疏才浅,难免存在些许错误,望留言指正 作…...
【Docker】在Windows下使用Docker Desktop创建nginx容器并访问默认网站
欢迎来到《小5讲堂》,大家好,我是全栈小5。 这是《Docker容器》序列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
