快速排序|超详细讲解|入门深入学习排序算法
快速排序介绍
快速排序(Quick Sort)使用分治法策略。
它的基本思想是:选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分;其中一部分的所有数据都比另外一部分的所有数据都要小。然后,再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序流程:
(1) 从数列中挑出一个基准值。
(2) 将所有比基准值小的摆放在基准前面,所有比基准值大的摆在基准的后面(相同的数可以到任一边);在这个分区退出之后,该基准就处于数列的中间位置。
(3) 递归地把"基准值前面的子数列"和"基准值后面的子数列"进行排序。
快速排序图文说明
/** 快速排序** 参数说明:* a -- 待排序的数组* l -- 数组的左边界(例如,从起始位置开始排序,则l=0)* r -- 数组的右边界(例如,排序截至到数组末尾,则r=a.length-1)*/
void quick_sort(int a[], int l, int r)
{if (l < r){int i,j,x;i = l;j = r;x = a[i];while (i < j){while(i < j && a[j] > x)j--; // 从右向左找第一个小于x的数if(i < j)a[i++] = a[j];while(i < j && a[i] < x)i++; // 从左向右找第一个大于x的数if(i < j)a[j--] = a[i];}a[i] = x;quick_sort(a, l, i-1); /* 递归调用 */quick_sort(a, i+1, r); /* 递归调用 */}
}下面以数列a={30,40,60,10,20,50}为例,演示它的快速排序过程(如下图)。
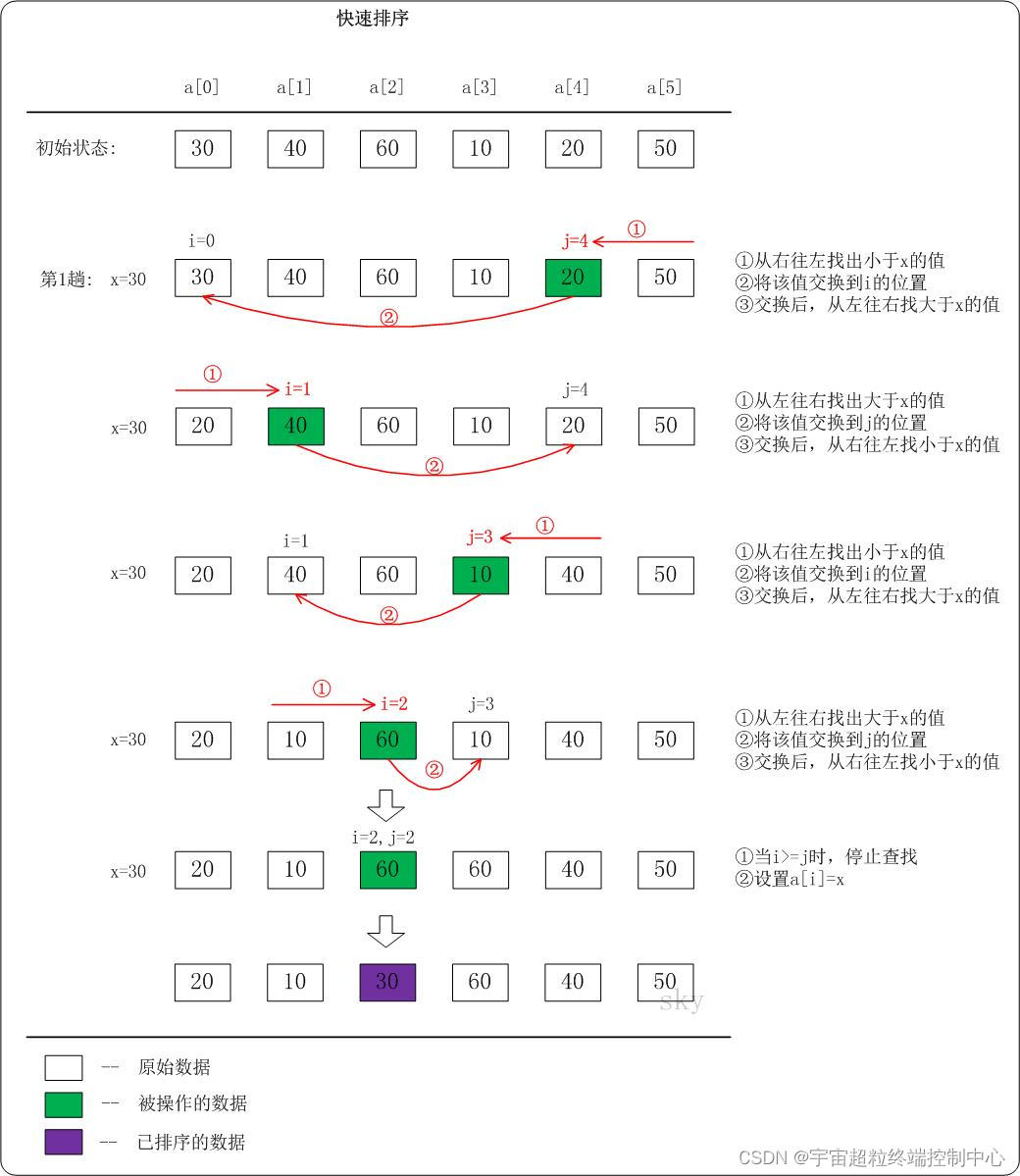
上图只是给出了第1趟快速排序的流程。在第1趟中,设置x=a[i],即x=30。
(01) 从"右 --> 左"查找小于x的数:找到满足条件的数a[j]=20,此时j=4;然后将a[j]赋值a[i],此时i=0;接着从左往右遍历。
(02) 从"左 --> 右"查找大于x的数:找到满足条件的数a[i]=40,此时i=1;然后将a[i]赋值a[j],此时j=4;接着从右往左遍历。
(03) 从"右 --> 左"查找小于x的数:找到满足条件的数a[j]=10,此时j=3;然后将a[j]赋值a[i],此时i=1;接着从左往右遍历。
(04) 从"左 --> 右"查找大于x的数:找到满足条件的数a[i]=60,此时i=2;然后将a[i]赋值a[j],此时j=3;接着从右往左遍历。
(05) 从"右 --> 左"查找小于x的数:没有找到满足条件的数。当i>=j时,停止查找;然后将x赋值给a[i]。此趟遍历结束!按照同样的方法,对子数列进行递归遍历。最后得到有序数组!
时间复杂度和稳定性
快速排序稳定性
快速排序是不稳定的算法,它不满足稳定算法的定义。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
快速排序时间复杂度
快速排序的时间复杂度在最坏情况下是O(N2),平均的时间复杂度是O(N*lgN)。
这句话很好理解:假设被排序的数列中有N个数。遍历一次的时间复杂度是O(N),需要遍历多少次呢?至少lg(N+1)次,最多N次。
(01) 为什么最少是lg(N+1)次?快速排序是采用的分治法进行遍历的,我们将它看作一棵二叉树,它需要遍历的次数就是二叉树的深度,而根据完全二叉树的定义,它的深度至少是lg(N+1)。因此,快速排序的遍历次数最少是lg(N+1)次。
(02) 为什么最多是N次?这个应该非常简单,还是将快速排序看作一棵二叉树,它的深度最大是N。因此,快读排序的遍历次数最多是N次。
代码实现
C语言实现
/*** 快速排序:C 语言** @author skywang* @date 2014/03/11*/#include <stdio.h>// 数组长度
#define LENGTH(array) ( (sizeof(array)) / (sizeof(array[0])) )/** 快速排序** 参数说明:* a -- 待排序的数组* l -- 数组的左边界(例如,从起始位置开始排序,则l=0)* r -- 数组的右边界(例如,排序截至到数组末尾,则r=a.length-1)*/
void quick_sort(int a[], int l, int r)
{if (l < r){int i,j,x;i = l;j = r;x = a[i];while (i < j){while(i < j && a[j] > x)j--; // 从右向左找第一个小于x的数if(i < j)a[i++] = a[j];while(i < j && a[i] < x)i++; // 从左向右找第一个大于x的数if(i < j)a[j--] = a[i];}a[i] = x;quick_sort(a, l, i-1); /* 递归调用 */quick_sort(a, i+1, r); /* 递归调用 */}
}void main()
{int i;int a[] = {30,40,60,10,20,50};int ilen = LENGTH(a);printf("before sort:");for (i=0; i<ilen; i++)printf("%d ", a[i]);printf("\n");quick_sort(a, 0, ilen-1);printf("after sort:");for (i=0; i<ilen; i++)printf("%d ", a[i]);printf("\n");
}c++实现
/*** 快速排序:C++** @author skywang* @date 2014/03/11*/#include <iostream>
using namespace std;/** 快速排序** 参数说明:* a -- 待排序的数组* l -- 数组的左边界(例如,从起始位置开始排序,则l=0)* r -- 数组的右边界(例如,排序截至到数组末尾,则r=a.length-1)*/
void quickSort(int* a, int l, int r)
{if (l < r){int i,j,x;i = l;j = r;x = a[i];while (i < j){while(i < j && a[j] > x)j--; // 从右向左找第一个小于x的数if(i < j)a[i++] = a[j];while(i < j && a[i] < x)i++; // 从左向右找第一个大于x的数if(i < j)a[j--] = a[i];}a[i] = x;quickSort(a, l, i-1); /* 递归调用 */quickSort(a, i+1, r); /* 递归调用 */}
}int main()
{int i;int a[] = {30,40,60,10,20,50};int ilen = (sizeof(a)) / (sizeof(a[0]));cout << "before sort:";for (i=0; i<ilen; i++)cout << a[i] << " ";cout << endl;quickSort(a, 0, ilen-1);cout << "after sort:";for (i=0; i<ilen; i++)cout << a[i] << " ";cout << endl;return 0;
}java实现
/*** 快速排序:Java** @author skywang* @date 2014/03/11*/public class QuickSort {/** 快速排序** 参数说明:* a -- 待排序的数组* l -- 数组的左边界(例如,从起始位置开始排序,则l=0)* r -- 数组的右边界(例如,排序截至到数组末尾,则r=a.length-1)*/public static void quickSort(int[] a, int l, int r) {if (l < r) {int i,j,x;i = l;j = r;x = a[i];while (i < j) {while(i < j && a[j] > x)j--; // 从右向左找第一个小于x的数if(i < j)a[i++] = a[j];while(i < j && a[i] < x)i++; // 从左向右找第一个大于x的数if(i < j)a[j--] = a[i];}a[i] = x;quickSort(a, l, i-1); /* 递归调用 */quickSort(a, i+1, r); /* 递归调用 */}}public static void main(String[] args) {int i;int a[] = {30,40,60,10,20,50};System.out.printf("before sort:");for (i=0; i<a.length; i++)System.out.printf("%d ", a[i]);System.out.printf("\n");quickSort(a, 0, a.length-1);System.out.printf("after sort:");for (i=0; i<a.length; i++)System.out.printf("%d ", a[i]);System.out.printf("\n");}
}上面3种语言的实现原理和输出结果都是一样的。下面是它们的输出结果:
before sort:30 40 60 10 20 50 after sort:10 20 30 40 50 60
相关文章:

快速排序|超详细讲解|入门深入学习排序算法
快速排序介绍 快速排序(Quick Sort)使用分治法策略。 它的基本思想是:选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分;其中一部分的所有数据都比另外一部分的所有数据都要小。然后,再按此方法对这两部分数据分别进…...
指针+一维整型数组的基本运用 和 指针+一维整型数组的初步学习
一,调式程序的技巧: 1.明确问题 2.定位问题 3.加打印(打印核心数据0) 二,指针的回顾 1.指针的概念:指针就是地址(内存单元的编号),是一个数据类型(指针类型…...

APP测试基本流程以及APP测试要点总结
🍅 视频学习:文末有免费的配套视频可观看 🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 APP测试实际上依然属于软件测试的范畴,是软件测试的一个真子集,所以经典软…...

GPT-4 Vision调试任何应用,即使缺少文本日志 升级Streamlit七
GPT-4 Vision 系列: 翻译: GPT-4 with Vision 升级 Streamlit 应用程序的 7 种方式一翻译: GPT-4 with Vision 升级 Streamlit 应用程序的 7 种方式二翻译: GPT-4 Vision静态图表转换为动态数据可视化 升级Streamlit 三翻译: GPT-4 Vision从图像转换为完全可编辑的表格 升级St…...

ppt形状导入draw.io
draw.io里面的形状还是有点少,我有时想找一个形状,发现PPT里有,但draw.io里有,比如 也就是这个形状 最简单的想法就是我直接把这个形状在PPT里存成图片(png),然后再导入到draw.io里,但是结果是…...
GoLang和GoLand的安装和配置
1. GoLang 1.1 特点介绍 Go 语言保证了既能达到静态编译语言的安全和性能,又达到了动态语言开发维护的高效率,使用一个表达式来形容 Go 语言:Go C Python , 说明 Go 语言既有 C 静态语言程序的运行速度,又能达到 Python 动态语…...

BGAD文章复现笔记-1
文章名:《Explicit Boundary Guided Semi-Push-Pull Contrastive Learning for Supervised Anomaly Detection》 原作者代码:https://github.com/xcyao00/BGAD 复现过程: 系统Ubuntu22.04, PyTorch1.12.1,python3.9 下载原作者…...
【EI会议推荐】第六届下一代数据驱动网络国际学术会议(NGDN 2024)
第六届下一代数据驱动网络国际学术会议(NGDN 2024) The Sixth International Conference on Next Generation Data-driven Networks 2024年4月26-28日 | 中国沈阳 *NGDN 2024已进入中国学术会议在线推荐列表:Click 基于前几届在英国埃克塞…...
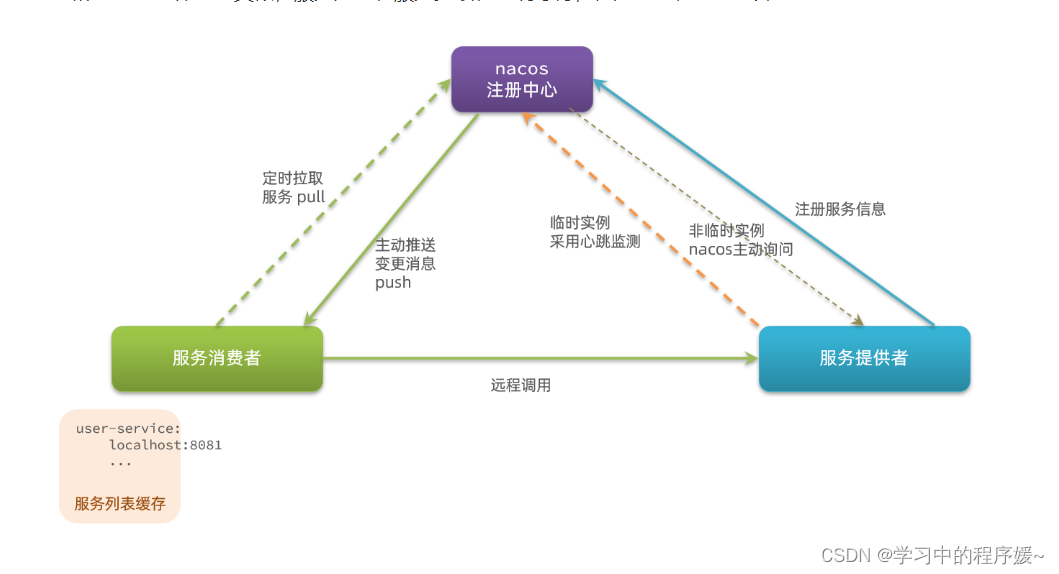
聊聊java中的Eureka和Nacos
本文主要来自于黑马课程中 1.提供者与消费者 在服务调用关系中,会有两个不同的角色: 服务提供者:一次业务中,被其它微服务调用的服务。(提供接口给其它微服务) 服务消费者:一次业务中࿰…...

系统架构设计师-21年-上午试题
系统架构设计师-21年-上午试题 更多软考资料 https://ruankao.blog.csdn.net/ 1 ~ 10 1 前趋图(Precedence Graph)是一个有向无环图,记为:→{(Pi,Pj)|Pi must complete before Pj may strat},假设系统中进程P{P1,P2,P3…...
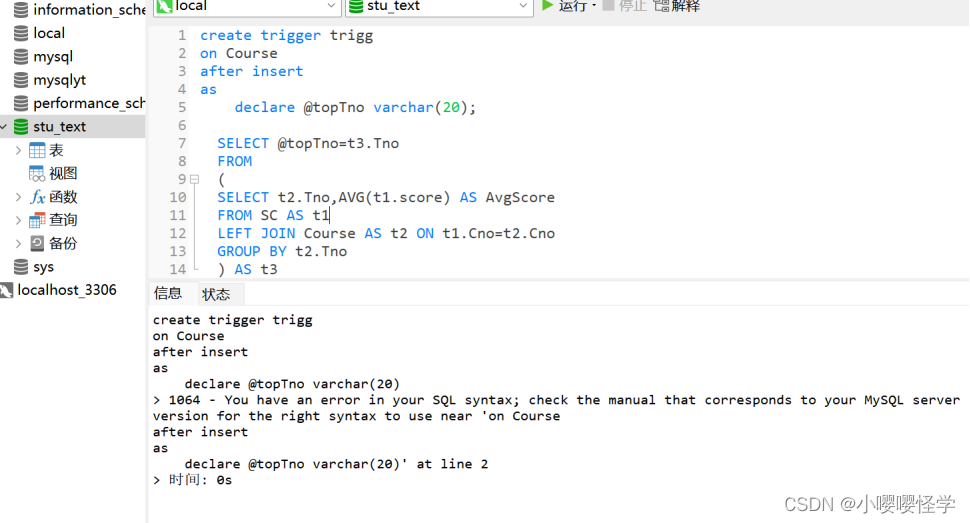
数据库MySQL查询设计||给定四个关联表,其定义和数据加载如下:-- 学生表 Student-- 选课表 SC
SQL查询设计 给定四个关联表,其定义和数据加载如下: -- 学生表 Student create table Student(Sno varchar(6), Sname varchar(10), Sdate datetime, Ssex varchar(10)); insert into Student values(01 , 赵雷 , 1999-01-01 , 男); insert into St…...
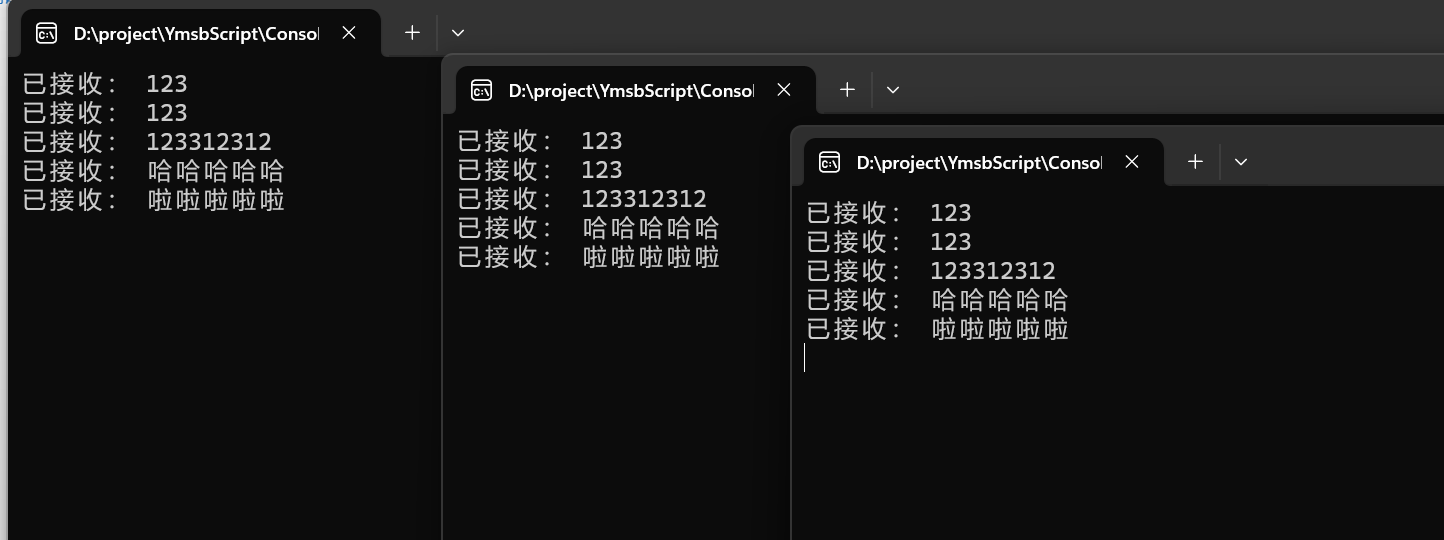
C#使用RabbitMQ-3_发布订阅模式(扇形交换机)
简介 发布订阅模式允许一个生产者向多个消费者发送消息。在RabbitMQ中实现发布订阅模式通常涉及以下几个关键组件: 生产者:负责生产并发送消息到RabbitMQ的Exchange(路由器)。Exchange:作为消息的中转站,…...
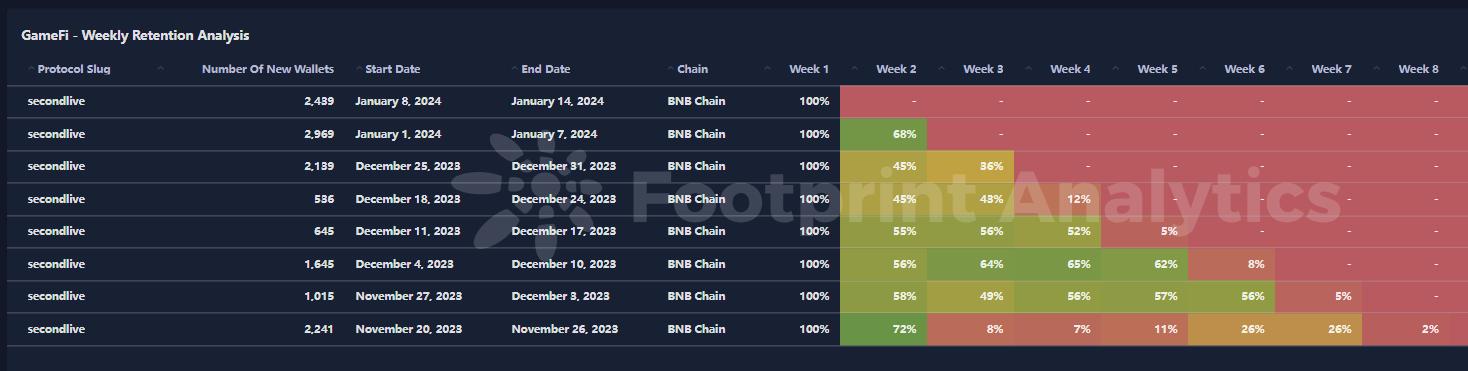
区块链游戏解说:什么是 SecondLive
数据源:SecondLive Dashboard 作者:lesleyfootprint.network 什么是 SecondLive SecondLive 是元宇宙居民的中心枢纽,拥有超过100 万用户的蓬勃社区。它的主要使命是促进自我表达,释放创造力,构建梦想中的平行宇宙…...

构建基于Flask的跑腿外卖小程序
跑腿外卖小程序作为现代生活中的重要组成部分,其技术实现涉及诸多方面,其中Web开发框架是至关重要的一环。在这篇文章中,我们将使用Python的Flask框架构建一个简单的跑腿外卖小程序的原型,展示其基本功能和实现原理。 首先&…...

【算法】Partitioning the Array(数论)
题目 Allen has an array a1,a2,…,an. For every positive integer k that is a divisor of n, Allen does the following: He partitions the array into n/k disjoint subarrays of length k. In other words, he partitions the array into the following subarrays: [a1,…...

ASP.NET Core 7 Web 使用Session
ASP.NET Core 好像不能像20年前那样直接使用Session函数,我使用如下方法 1、在NuGet安装以下2个包 2、在Program.cs注册 //注册Session builder.Services.AddSession(options > {options.IdleTimeout TimeSpan.FromMinutes(60);options.Cookie.HttpOnly fals…...

(1)SpringBoot学习——芋道源码
Spring Boot 的快速入门 一.、概述 使用 Spring Boot 可以很容易地创建出能直接运行的独立的、生产级别的基于 Spring 的应用。 二、快速入门 2.1 创建 Maven 项目 打开 IDEA,点击菜单 File -> New -> Project.来创建项目选择 Maven 类型,点击「…...

宏景eHR FrCodeAddTreeServlet SQL注入漏洞复现
前言 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该文章仅供学习用途使用。 一、产…...
STM32——I2C
通信协议见(STM32——SPI) 一、I2C协议 1.1 I2C协议介绍; I2C是(Inter IC Bus)是由Philips公司开发的一种通用数据总线; 有多根通信线; 一根SDA(串行通信线)…...

笔记本从零安装ubuntu server系统+环境配置
文章目录 前言相关链接ubuntu Server 安装教程屏幕自动息屏关上盖子不休眠MobaXterm外网SSH内网穿透IPV6远程 为什么我要笔记本装Linux为什么要换ubuntu Server版能否连接wifi之后Linux 配置清单总结 前言 之前装了个ubuntu desktop 版,发现没有命令行,…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
