【算法】Partitioning the Array(数论)
题目
Allen has an array a1,a2,…,an. For every positive integer k that is a divisor of n, Allen does the following:
-
He partitions the array into n/k disjoint subarrays of length k. In other words, he partitions the array into the following subarrays:
[a1,a2,…,ak],[ak+1,ak+2,…,a2k],…,[an−k+1,an−k+2,…,an]
-
Allen earns one point if there exists some positive integer m (m≥2) such that if he replaces every element in the array with its remainder when divided by m, then all subarrays will be identical.
Help Allen find the number of points he will earn.
================================================================
Allen 有一个数组 a1,a2,…,an。对于每一个能被 n 整除的正整数 k,艾伦都会做如下运算:
-
他将数组划分为长度为 k 的 n/k 个互不相交的子数组:
[a1,a2,…,ak],[ak+1,ak+2,…,a2k],…,[an−k+1,an−k+2,…,an]
-
如果存在某个正整数 m (m≥2),使得如果他把数组中的每个元素都替换成除以 m 后的余数,那么所有的子数组都是相同的,Allen 就可以得到一分。
帮助艾伦找出他将获得的分数。
Input
Each test consists of multiple test cases. The first line contains a single integer t (1≤t≤104) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer n (1≤n≤2⋅10^5) — the length of the array a.
The second line of each test case contains n integers a1,a2,…,an (1≤ai≤n) — the elements of the array a.
It is guaranteed that the sum of n over all test cases does not exceed 2⋅105.
输入
每个测试由多个测试用例组成。第一行包含一个整数 t(1≤t≤104)–测试用例数。测试用例说明如下。
每个测试用例的第一行包含一个整数 n(1≤n≤2⋅105)–数组 a 的长度。
每个测试用例的第二行包含 n 个整数 a1,a2,…,an(1≤ai≤n)–数组 a 的元素。
保证所有测试用例中 n 的总和不超过 2⋅10^5。
Output
For each test case, output a single integer — the number of points Allen will earn.
输出
对于每个测试用例,输出一个整数 - 艾伦将获得的分数。
思路
本题用到一个概念:如果m为|x-y|的因数,则x % m == y % m.
将数组划分为长度相等的 i 段,将所有的数全部模m之后,所有数组相同。例如当m = 1的时候每个数组中的数均为0,(当然题目中要求m != 0,这里只是做个假设)可以得到一分。
若 n % k == 0,将数组分成了k段
则原数组中m 必须为 abs(h[ i ] - h[ i + k])的因数.

代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n;
int h[N];int gcd(int a, int b) // 欧几里得算法
{return b ? gcd(b, a % b) : a;
}void solve()
{cin >> n;int ans = 0;for(int i = 1; i <= n; i ++) cin >> h[i];for(int i = 1; i <= n; i ++){if(n % i == 0){int m = 0;for(int k = 1; k + i <= n; k ++){m = gcd(m,abs(h[i + k] - h[k]));}ans += (m != 1);}}cout << ans << endl;
}int main()
{int t;cin >> t;while(t --)solve();return 0;
}
题目来自:Partitioning the Array
相关文章:

【算法】Partitioning the Array(数论)
题目 Allen has an array a1,a2,…,an. For every positive integer k that is a divisor of n, Allen does the following: He partitions the array into n/k disjoint subarrays of length k. In other words, he partitions the array into the following subarrays: [a1,…...

ASP.NET Core 7 Web 使用Session
ASP.NET Core 好像不能像20年前那样直接使用Session函数,我使用如下方法 1、在NuGet安装以下2个包 2、在Program.cs注册 //注册Session builder.Services.AddSession(options > {options.IdleTimeout TimeSpan.FromMinutes(60);options.Cookie.HttpOnly fals…...

(1)SpringBoot学习——芋道源码
Spring Boot 的快速入门 一.、概述 使用 Spring Boot 可以很容易地创建出能直接运行的独立的、生产级别的基于 Spring 的应用。 二、快速入门 2.1 创建 Maven 项目 打开 IDEA,点击菜单 File -> New -> Project.来创建项目选择 Maven 类型,点击「…...

宏景eHR FrCodeAddTreeServlet SQL注入漏洞复现
前言 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该文章仅供学习用途使用。 一、产…...
STM32——I2C
通信协议见(STM32——SPI) 一、I2C协议 1.1 I2C协议介绍; I2C是(Inter IC Bus)是由Philips公司开发的一种通用数据总线; 有多根通信线; 一根SDA(串行通信线)…...

笔记本从零安装ubuntu server系统+环境配置
文章目录 前言相关链接ubuntu Server 安装教程屏幕自动息屏关上盖子不休眠MobaXterm外网SSH内网穿透IPV6远程 为什么我要笔记本装Linux为什么要换ubuntu Server版能否连接wifi之后Linux 配置清单总结 前言 之前装了个ubuntu desktop 版,发现没有命令行,…...

SQL 快速参考手册
SQL 语句语法AND / ORSELECT column_name(s) FROM table_name WHERE condition AND|OR conditionALTER TABLEALTER TABLE table_name ADD column_name datatype 或者: ALTER TABLE table_name DROP COLUMN column_name AS (alias)SELECT column_name AS column_alia…...

Linux/Windows系统无法git clone解决办法
一、Windows 1. 查找github和githubusercontent的IP地址 IP Tracer & Tracker - IP Address Lookup Made EasyIP Lookup Made Easy Using The Best IP Tracker – Trace An IP, Map The Location & Get Accurate Results When Using The Best IP Finderhttps://www.i…...
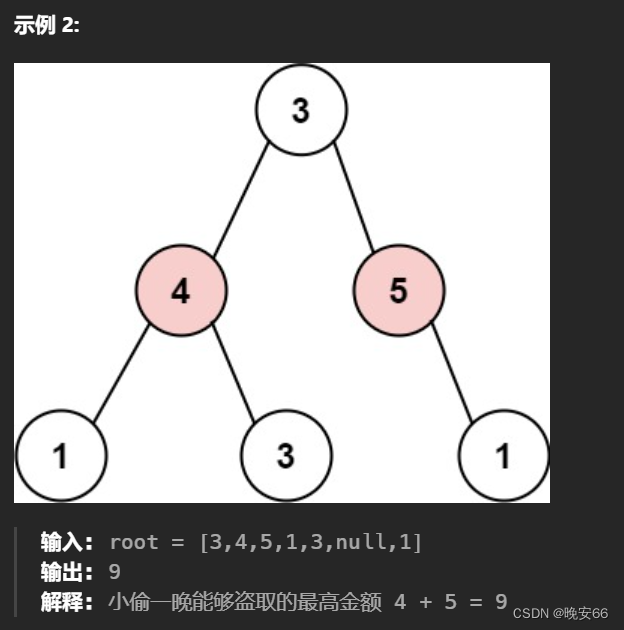
【算法与数据结构】198、213、337LeetCode打家劫舍I, II, III
文章目录 一、198、打家劫舍二、213、打家劫舍 II三、337、打家劫舍III三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、198、打家劫舍 思路分析:打家劫舍是动态规划的的经典题目。本题的难点在于递归公式…...

React、React Router、JSX 简单入门快速上手
React、React Router、JSX 简单入门快速上手 介绍特点 JSX使用js表达式渲染列表样式控制注意事项 入门脚手架创建react项目安装目录介绍入口文件解析 组件解析介绍函数式组件类组件 事件绑定注意点定义使用事件对象事件处理函数接收额外参数 组件状态状态的定义使用 组件通信父…...

从 0 开始搭建 React 框架
webpack 配置 不再赘述,可参考前三个文章(wenpack5 基本使用 1 - 3) 使用 react 安装 react、react-dom、babel/preset-react yarn add react react-dom babel/preset-react<!DOCTYPE html> <html lang"en"> <h…...

网站地址怎么改成HTTPS?
现在,所有类型的网站都需要通过 HTTPS 协议进行安全连接,而实现这一目标的唯一方法是使用 SSL 证书。如果您不将 HTTP 转换为 HTTPS,浏览器和应用程序会将您网站的连接标记为不安全。 但用户询问如何将我的网站从 HTTP 更改为 HTTPS。在此页…...
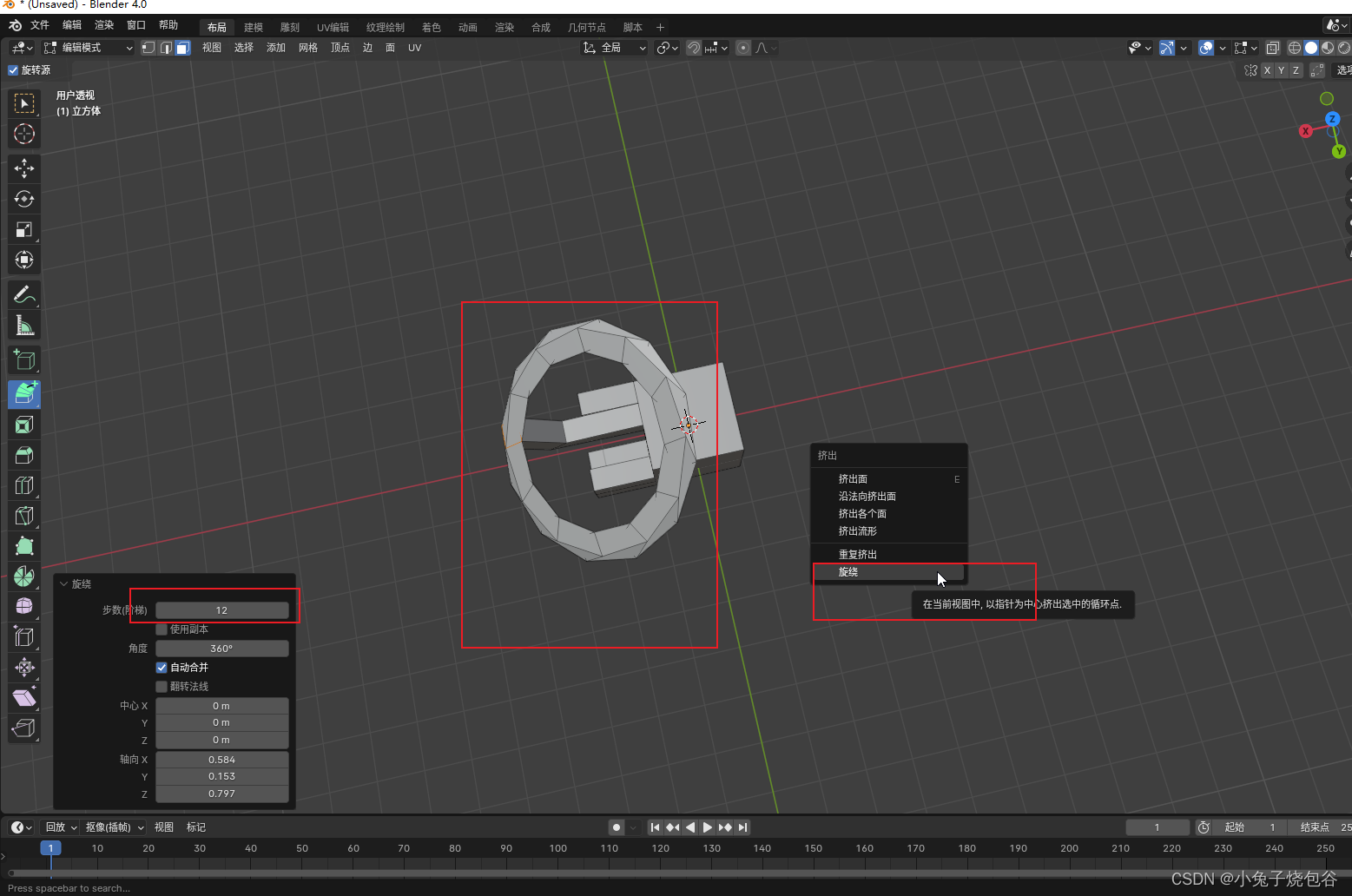
Blender教程(基础)-面的细分与删除、挤出选区-07
一、Blender之面的细分 新建一个立方体,在编辑模式下、选中一个面。 在选中的面上单击右键弹出细分选项,选择细分。 在选中细分后、会默认细分1次。修改细分次数在左下角 二、Blender之面的删除 选择中需要操作的面,在英文状态下按X键弹…...

QT自制软键盘 最完美、最简单、支持中文输入(二)
目录 一、前言 二、本自制虚拟键盘特点 三、中文输入原理 四、组合键输入 五、键盘事件模拟 六、界面 七、代码 7.1 frmKeyBoard 头文件代码 7.2 frmKeyBoard 源文件代码 八、使用示例 九、效果 十、结语 一、前言 由于系统自带虚拟键盘不一定好用,也不一…...

SpringCloud_学习笔记_1
SpringCloud01 1.认识微服务 随着互联网行业的发展,对服务的要求也越来越高,服务架构也从单体架构逐渐演变为现在流行的微服务架构。这些架构之间有怎样的差别呢? 1.0.学习目标 了解微服务架构的优缺点 1.1.单体架构 单体架构ÿ…...

容器算法迭代器初识
#include<iostream> using namespace std; #include<vector> //vetor容器存放内置数据类型 void test01() {//创建了一个vector容器,数组 vector<int> v;//向容器中插入数据v.push_back (10);//尾插 v.push_back (20);v.push_back (30);v.push_ba…...

瑞_力扣LeetCode_二叉搜索树相关题
文章目录 说明题目 450. 删除二叉搜索树中的节点题解递归实现 题目 701. 二叉搜索树中的插入操作题解递归实现 题目 700. 二叉搜索树中的搜索题解递归实现 题目 98. 验证二叉搜索树题解中序遍历非递归实现中序遍历递归实现上下限递归 题目 938. 二叉搜索树的范围和题解中序遍历…...

python爬虫爬取网站
流程: 1.指定url(获取网页的内容) 爬虫会向指定的URL发送HTTP请求,获取网页的HTML代码,然后解析HTML代码,提取出需要的信息,如文本、图片、链接等。爬虫请求URL的过程中,还可以设置请求头、请求参数、请求…...
c# Get方式调用WebAPI,WebService等接口
/// <summary> /// 利用WebRequest/WebResponse进行WebService调用的类 /// </summary> public class WebServiceHelper {//<webServices>// <protocols>// <add name"HttpGet"/>// <add name"HttpPost"/>// …...

银行数据仓库体系实践(11)--数据仓库开发管理系统及开发流程
数据仓库管理着整个银行或公司的数据,数据结构复杂,数据量庞大,任何一个数据字段的变化或错误都会引起数据错误,影响数据应用,同时业务的发展也带来系统不断升级,数据需求的不断增加,数据仓库需…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
