C++ 数论相关题目 博弈论 Nim游戏
给定 n
堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 n
。
第二行包含 n
个数字,其中第 i
个数字表示第 i
堆石子的数量。
输出格式
如果先手方必胜,则输出 Yes。
否则,输出 No。
数据范围
1≤n≤105
,
1≤每堆石子数≤109
输入样例:
2
2 3
输出样例:
Yes
先手必胜状态:可以走到某一个必败状态
先手必败状态:走不到任何一个必败状态
几种状态:
(1)全部是0,异或起来也是0。(必败态)
(2)异或起来不是0,若等于x,x的第k位为1的话,则一定存在一个ai的第k位等于1,则从ai中拿走ai-ai^x个石子,则剩下的异或为0。(证明:总存在一种拿法,使得拿完异或起来为0)
(3)异或起来是0,假设从ai中拿走一些,则剩下的异或起来一定不等于0,因为反正假设等于0,拿走前后的全部堆异起来有ai等于拿走部分后的ai,矛盾。

总结:刚拿到石子,异或起来为不为0,则一定存在某种取法,使得剩下的异或为0,后手任意操作后状态一定不为0,这样循环,先手总操作不为0,后手总操作为0,最终,必败态(全部取完全0)一定会被后手先遇到,则先手胜。反之后手胜。
分析猛如虎,代码很简单。只需要把每个数读进来,异或一遍,看是不是0就行。
#include <iostream>
#include <algorithm>using namespace std;int main ()
{int n;cin>>n;int res = 0;while (n -- ){int x;cin>>x;res ^= x;}if(res) puts("Yes");else puts("No");return 0;
}
相关文章:

C++ 数论相关题目 博弈论 Nim游戏
给定 n 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。 问如果两人都采用最优策略,先手是否必胜。 输入格式…...
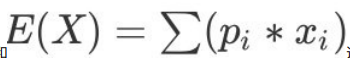
机器学习---无偏估计
1. 如何理解无偏估计 无偏估计:就是我认为所有样本出现的概率⼀样。 假如有N种样本我们认为所有样本出现概率都是 1/N。然后根据这个来计算数学期望。此时的数学期望就是我们平常讲 的平均值。数学期望本质就 是平均值。 2. 无偏估计为何叫做“无偏”࿱…...

C语言基础13
今天是学习嵌入式相关内容的第十四天,以下是今日所学内容 1.结构体: 1.结构体类型定义 2.结构体变量的定义 3.结构体元素的访问 4.结构体的存储 内存对齐 结构体整体的大小必须为最大基本类型长度的整数倍 5.结构体作为函数参数 值传递 练习:定…...

【Java】Maven配置加载到全局
Maven配置加载到全局 <build><plugins><plugin><artifactId>maven-resources-plugin</artifactId><configuration><encoding>utf-8</encoding><useDefaultDelimiters>true</useDefaultDelimiters></configura…...
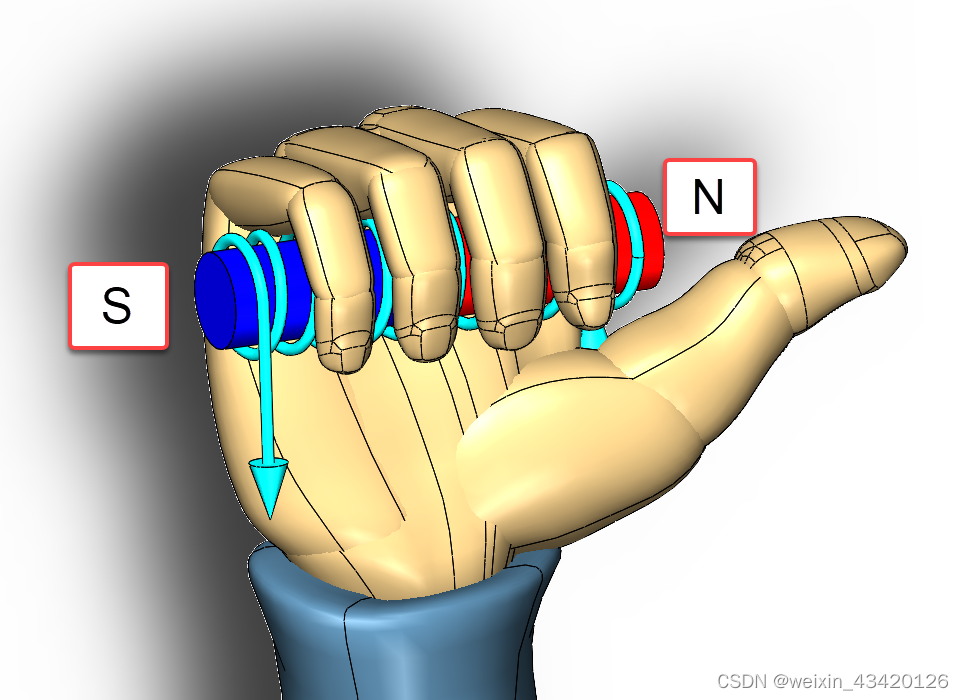
右手螺旋线定则
通电螺线管中的安培定则(安培定则二):用右手握住通电螺线管,让四指指向电流的方向,那么大拇指所指的那一端是通电螺线管的N极。...

2024 高级前端面试题之 React 「精选篇」
该内容主要整理关于 React 模块的相关面试题,其他内容面试题请移步至 「最新最全的前端面试题集锦」 查看。 React模块精选篇 1. 如何理解React State不可变性的原则2. JSX本质3. React合成事件机制4. setState和batchUpdate机制5. 组件渲染和更新过程6. Diff算法相…...
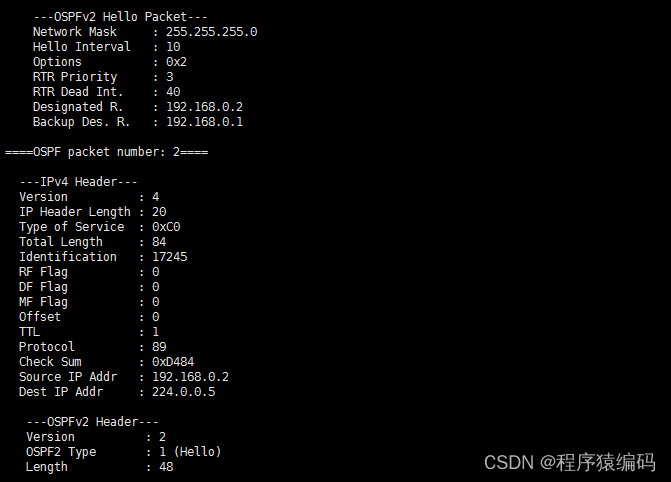
OSPF协议解析及相关技术探索(C/C++代码实现)
OSPF(开放最短路径优先)是一种用于自治系统(AS)内部的路由协议,它是基于链路状态算法的。OSPF的设计目的是为了提供一种可扩展、快速收敛和高效的路由解决方案。 OSPF概念和特点 概念 自治系统(AS&#…...
如何恢复已删除的照片?
在这篇综合文章中发现恢复丢失照片的有效且免费的方法。无论您使用的是智能手机、iPhone、Windows 计算机、Mac、SD 卡还是数码相机,我们都提供有关如何恢复已删除照片的分步说明。此外,学习一些有价值的技巧,以防止将来意外删除照片。 意外…...
VMware虚拟机安装macOS
VMware虚拟机安装macOS 文章目录 VMware虚拟机安装macOS先看效果一、准备工作①:镜像资源下载②:虚拟机③:安装macOS所必要的插件 二、开始安装①:创建新的虚拟机②:自定义硬件③:开启虚拟机 先看效果 一、…...
API管理协作工具:Apipost
相信无论是前端,还是后端的测试和开发人员,都遇到过这样的困难。不同工具之间数据一致性非常困难、低效。多个系统之间数据不一致,导致协作低效、频繁出问题,开发测试人员痛苦不堪。 API管理的难点在哪? 开发人员在 …...
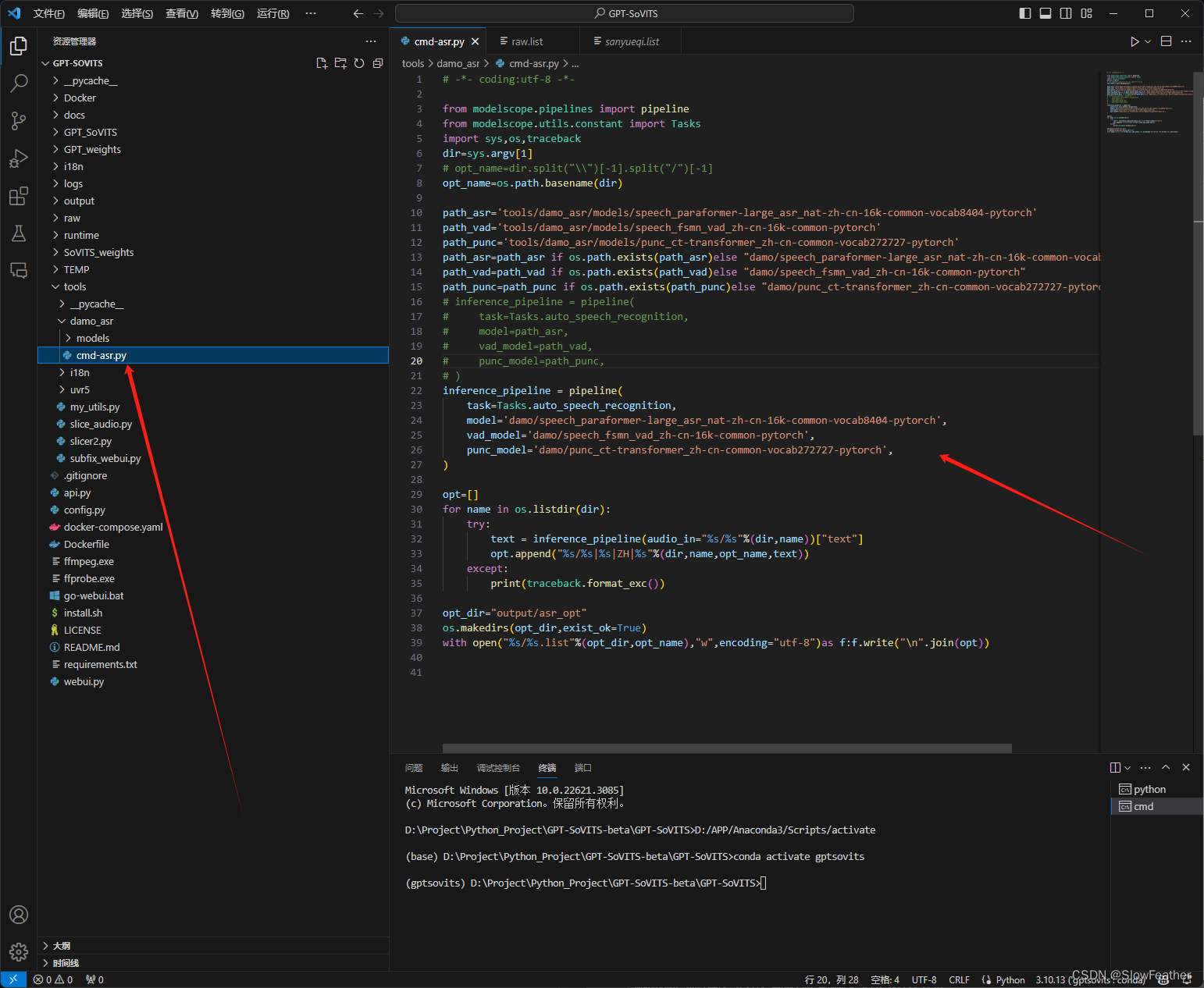
GPT-SoVITS 本地搭建踩坑
GPT-SoVITS 本地搭建踩坑 前言搭建下载解压VSCode打开安装依赖包修改内容1.重新安装版本2.修改文件内容 运行总结 前言 传言GPT-SoVITS作为当前与BertVits2.3并列的TTS大模型,于是本地搭了一个,简单说一下坑。 搭建 下载 到GitHub点击此处下载 http…...
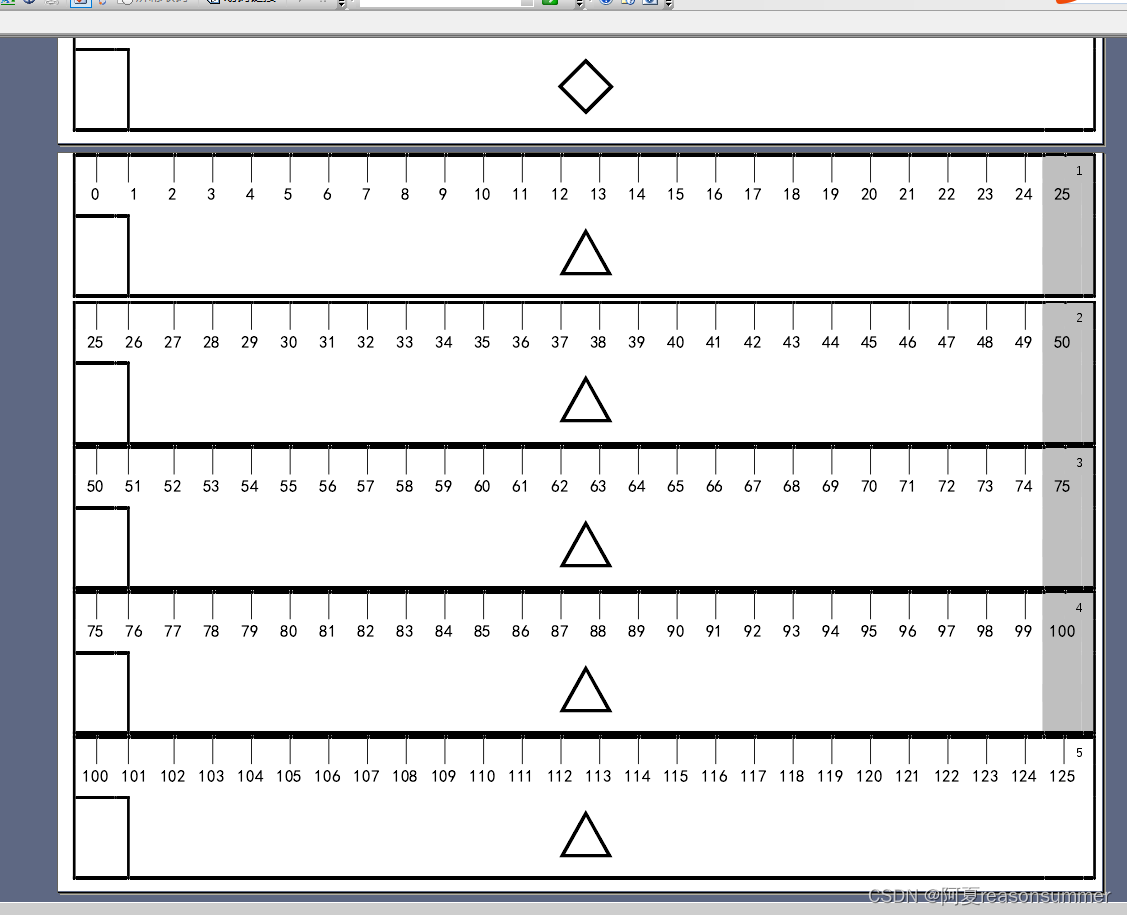
【教学类-34-02】20240130纸尺2.0 (A4横版5条,刻度25*5=125CM,有图案)
作品展示: 背景需求: 设计了纸尺的基本模板 【教学类-34-01】20240130纸尺1.0 (A4横版5条,刻度25*5125CM)-CSDN博客文章浏览阅读194次,点赞5次,收藏5次。【教学类-34-01】20240130纸尺1.0 &am…...
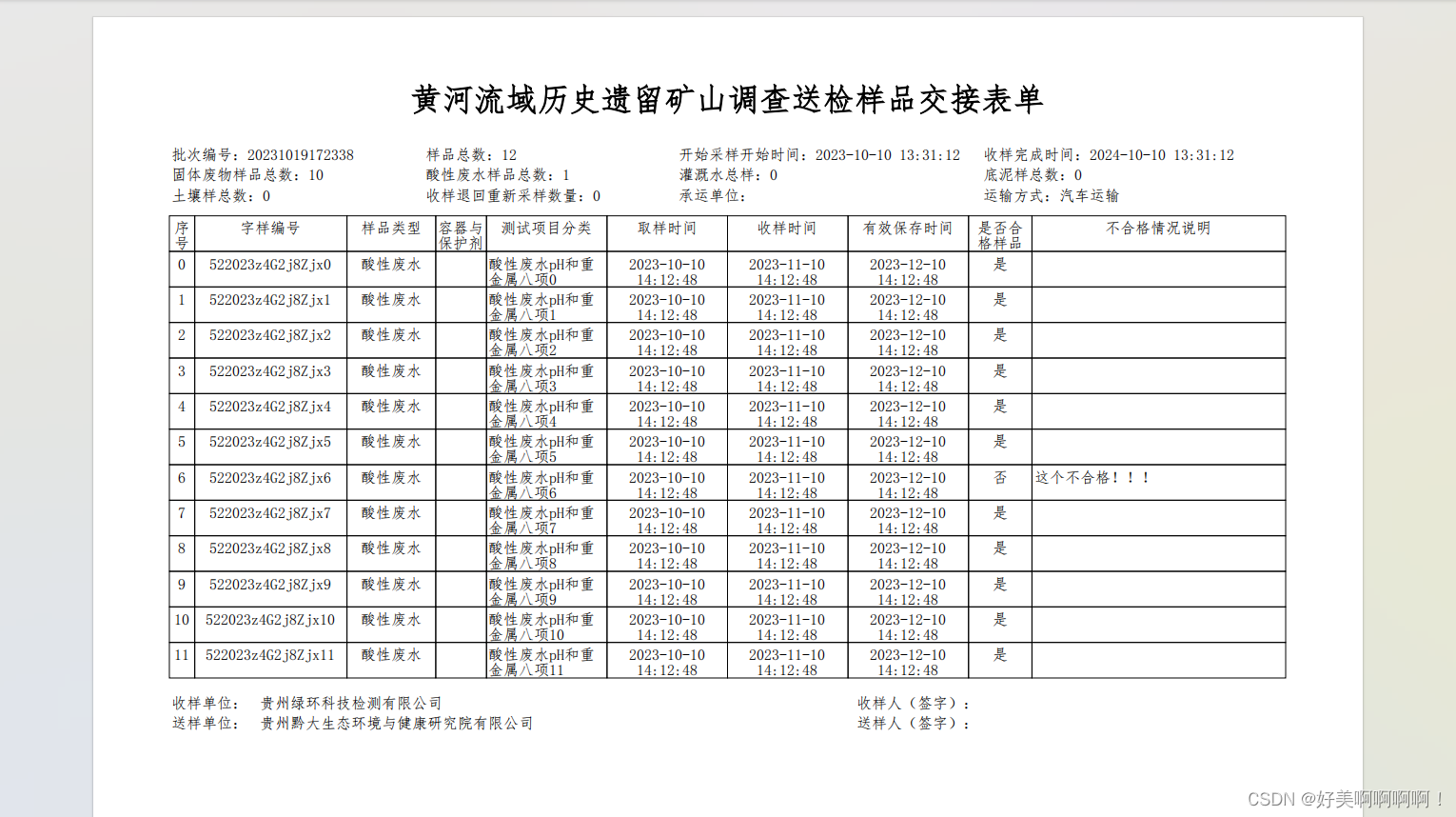
iText操作pdf
最近有个任务是动态的创建pdf根据获取到的内容,百度到的知识点都比较零散,官方文档想必大家也不容易看懂。下文是我做出的汇总 public class CreatePdfUtils {public static void create(){//准备File file new File("C:\\code\\base-project-back…...

关于SQLite 的下载与使用。配合python
win系统下: SQLite Download Page Precompiled Binaries for Windows sqlite-tools-win-x64-3450000.zip (4.77 MiB) 解压后,找个位置。然后设置环境变量指定位置。 可以手动建立.db文件。 也可以通过代码建立: 如下代码就是建立一个db文件。…...

java面向对象基础(面试)
一、面向对象基础 1. 面向对象和面向过程的区别 面向过程把解决问题的过程拆成一个个方法,通过一个个方法的执行解决问题。面向对象会先抽象出对象,然后用对象执行方法的方式解决问题。 2.创建一个对象用什么运算符?对象实体与对象引用有何不同? n…...

【C++修行之道】STL(初识list、stack)
目录 一、list 1.1list的定义和结构 以下是一个示例,展示如何使用list容器: 1.2list的常用函数 1.3list代码示例 二、stack 2.1stack的定义和结构 stack的常用定义 2.2常用函数 2.3stack代码示例 一、list 1.1list的定义和结构 list的使用频率不高&#…...
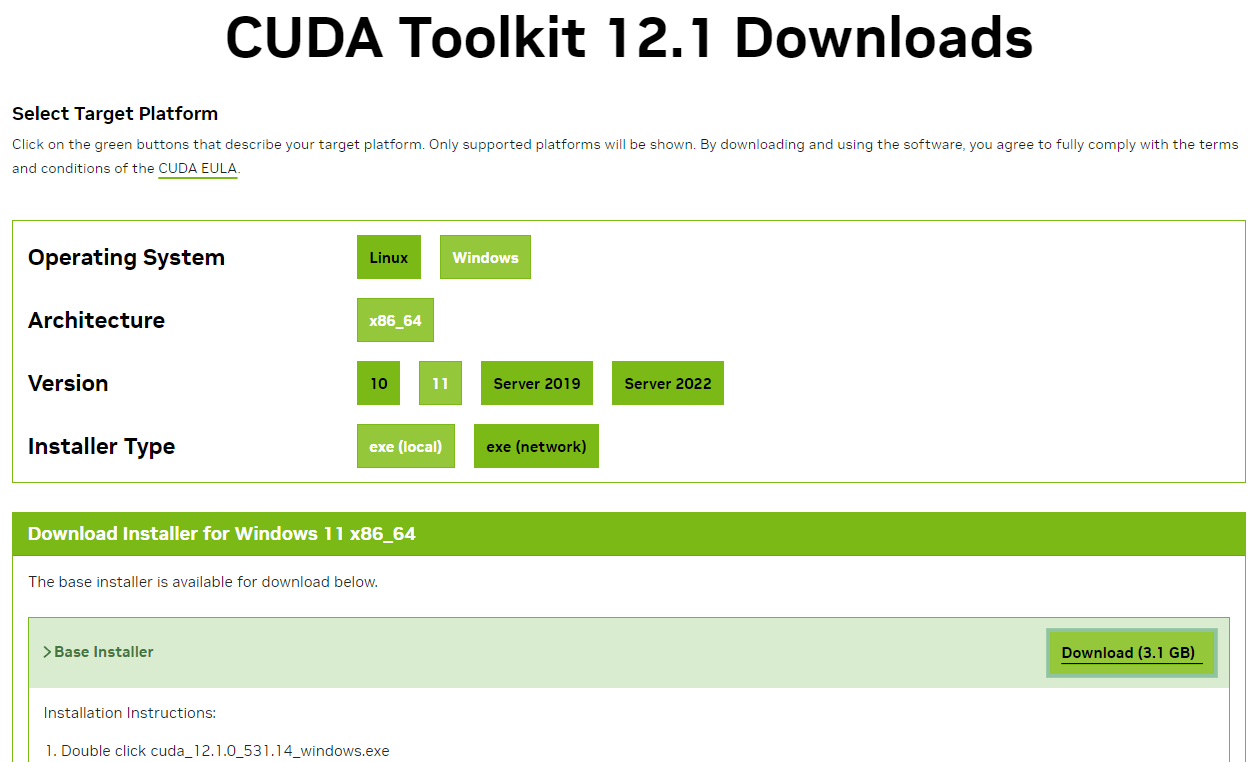
【环境配置】安装了pytorch但是报错torch.cuda.is_availabel()=Flase
解决思路:import torch正常,说明torch包安装正常,但是不能和gpu正常互动,猜测还是pytroch和cuda的配合问题 1.查看torch包所需的cuda版本 我的torch是2.0.1,在现在是比较新的包,需要12以上的cuda支持&…...

什么是模板方法模式?它的实现方式有哪些?
什么是模板方法模式?它的实现方式有哪些? 模板方法模式是一种行为型模式,它定义了一个操作中的算法骨架,而将算法的一些步骤延迟到子类中实现,使得子类可以不改变该算法结构的情况下重定义该算法的某些特定步骤。 模…...
)
java:实现查询MySQL数据库中的数据,并导出excel、pdf类型文档(超详细)
查询MySQL数据库中数据,导出excel、pdf类型文档 1.数据库表格 CREATE TABLE user (id int NOT NULL AUTO_INCREMENT COMMENT 编号,name varchar(255) DEFAULT NULL COMMENT 姓名,age int DEFAULT NULL COMMENT 年龄,addr varchar(255) DEFAULT NULL COMMENT 住址1…...
Java后端须知的前端知识
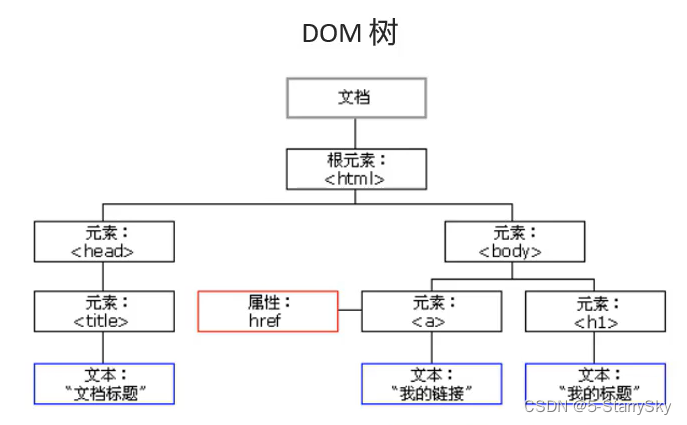
Java后端须知的前端知识 HTML (超文本标记语言) W3C标准 结构:HTML表现:CSS行为:JavaScript 快速入门 <html><head><title></title></head><body><font color"red&q…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
