Spring 中获取 Bean 对象的三种方式
目录
1、根据名称获取Bean
2、根据Bean类型获取Bean
3、根据 Bean 名称 + Bean 类型来获取 Bean(好的解决方法)
假设 Bean 对象是 User,并存储到 Spring 中,注册到 xml 文件中
public class User {public String sayHi(){return "hello world";}
}

下面我将列举获取 Bean 对象的几种方法
下面代码中 context 为 spring (上下文)对象
1、根据名称获取Bean
User user = (User) context.getBean("user");这种方式获取 Bean 只需要传入名称,即注册到 xml 文件中 Bean 的 id 。

同时我们还需要做一次对象类型强转,因为只传入 id ,getBean() 方法返回的是一个 Object 类型的对象。
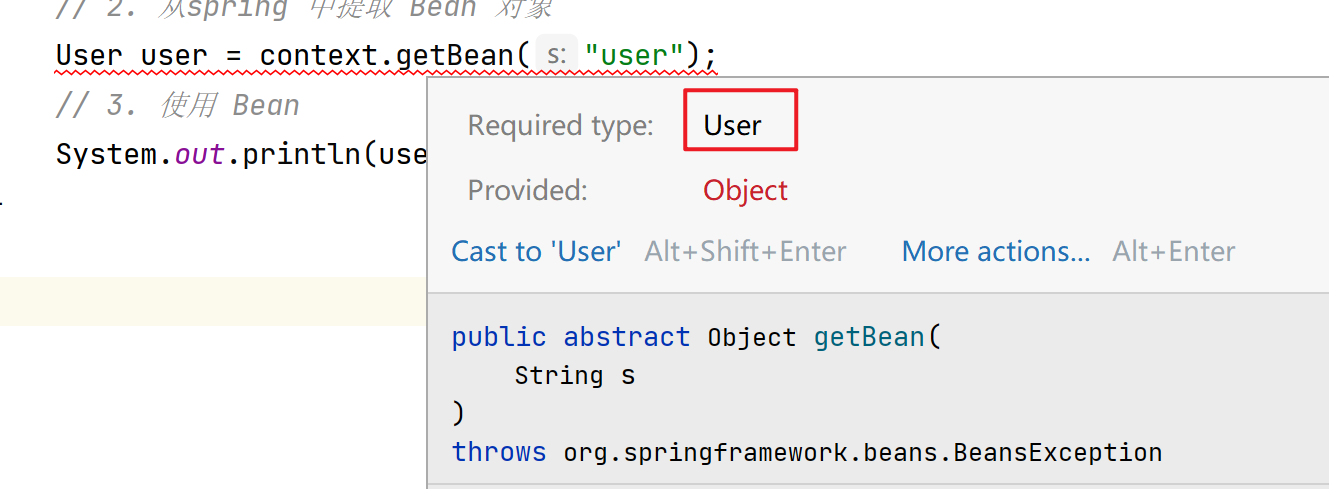
存在问题:当传入一个NULL时,强转 User 就会出错,报异常。
2、根据Bean类型获取Bean
User user = context.getBean(User.class);这种方式写法简单, 解决第一种方式传入 NULL 会报错的情况,但也存在一些问题,实际用途并不太多。
存在问题:当Spring中存在相同的对象是,使用类型来获取Bean就会报错

3、根据 Bean 名称 + Bean 类型来获取 Bean(好的解决方法)
User user = context.getBean("user", User.class);这种我们需要传入两个参数,一个是id,一个是对象类,返回一个该类的对象,就避免了强转的风险(第一种问题解决)。同时,我们在 spring 中存储多个相同对象时,也不回报错(第二种问题解决)。
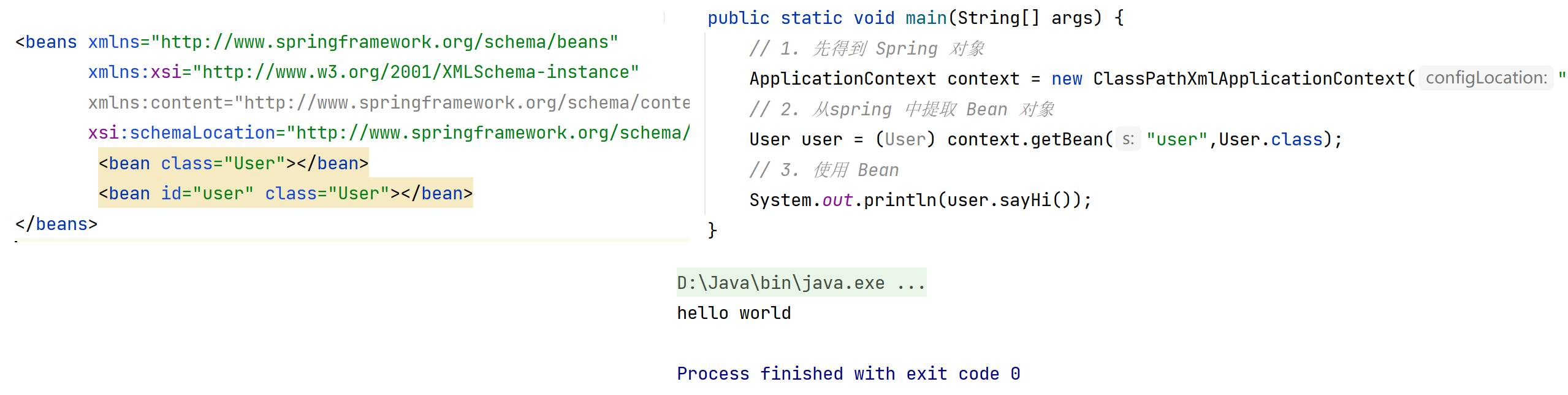
相关文章:

Spring 中获取 Bean 对象的三种方式
目录 1、根据名称获取Bean 2、根据Bean类型获取Bean 3、根据 Bean 名称 Bean 类型来获取 Bean(好的解决方法) 假设 Bean 对象是 User,并存储到 Spring 中,注册到 xml 文件中 public class User {public String sayHi(){retur…...

centos系统安装Ward服务器监控工具
简介 Ward是一个简约美观多系统支持的服务器监控面板 安装 1.首先安装jdk yum install java-1.8.0-openjdk-devel.x86_64 2.下载jar wget 3.启动 java -jar ward-1.8.8.jar 体验 浏览器输入 http://192.168.168.110:4000/ 设置服务名设置为:myserver 端口号:5000 点击…...

计算机网络-数据交换方式(电路交换 报文交换 分组交换及其两种方式 )
文章目录 为什么要数据交换?总览电路交换电路交换的各个阶段建立连接数据传输释放连接 电路交换的特点电路交换的优缺点 报文交换报文交换流程报文交换的优缺点 分组交换分组交换流程分组交换的优缺点 数据交换方式的选择分组交换的两种方式数据报方式数据报方式的特…...

【C++入门到精通】特殊类的设计 | 单例模式 [ C++入门 ]
阅读导航 引言一、设计模式概念(了解)二、单例模式1. 饿汉模式(1)概念(2)模拟实现(3)优缺点(4)适用场景 2. 懒汉模式(1)概念ÿ…...
【创建vue项目的两种方式】
Vue环境搭建 NodeJs安装包安装淘宝镜像 环境搭建webpack安装全局安装vue/cli查看模板创建项目1.webpack2. vue-cli NodeJs安装包 下载链接:官网链接 下载下来后,直接傻瓜式的安装即可。 通过在cmd控制台输入以下命令查看是否安装成功 node -v因为适配某…...
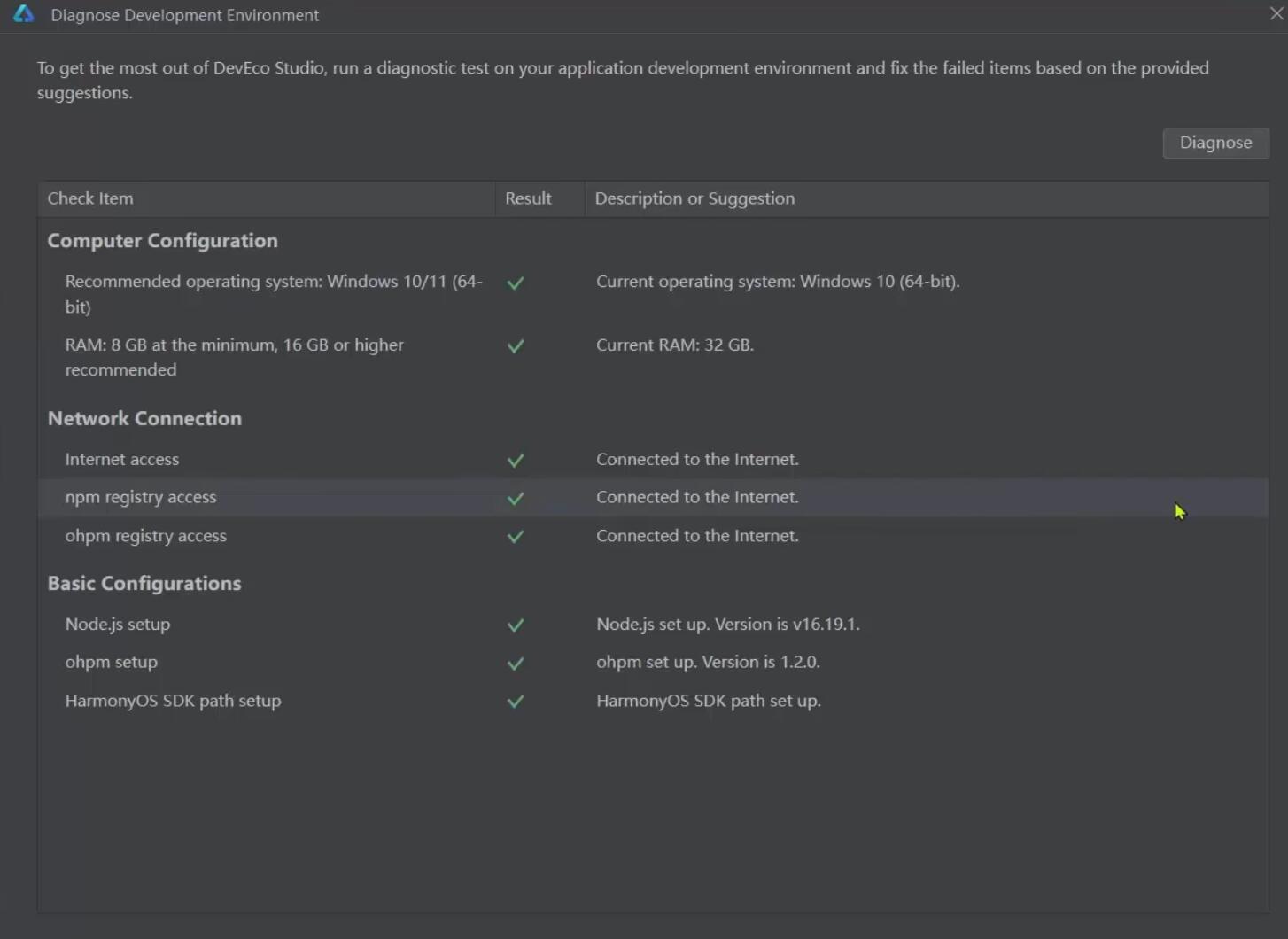
2. HarmonyOS应用开发DevEcoStudio准备-1
2. HarmonyOS应用开发DevEcoStudio准备-1 下载 DevEco Studio 进入HUAWEI DevEco Studio产品页产品页。 单击下载列表右侧的按钮,下载 DevEco Studio。 安装 DevEco Studio 下载完成后,双击下载的 deveco-studio-xxxx.exe,进入 DevEco St…...
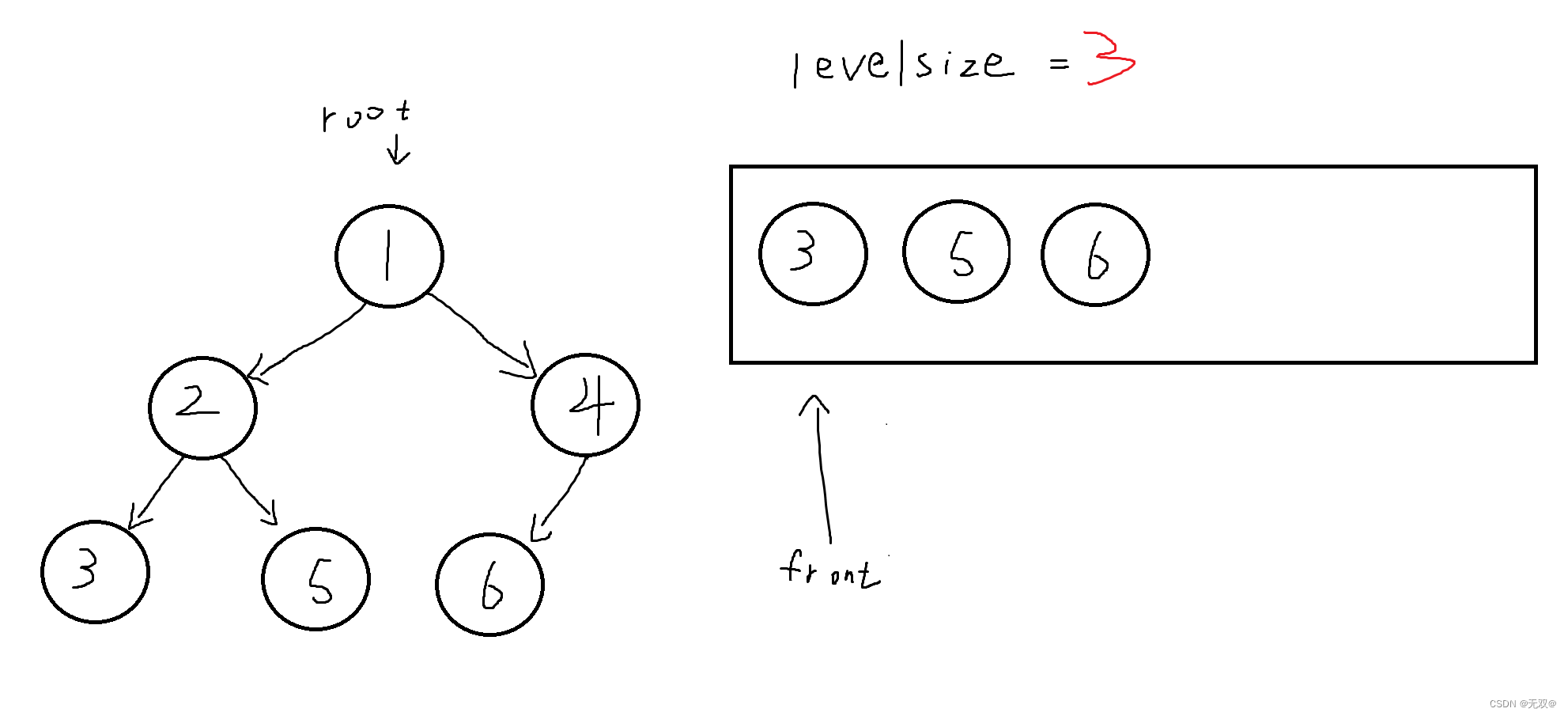
《二叉树》——3(层序遍历)
目录 前言: 层序遍历: 解析: 前言: 本文主讲链式二叉树的层序遍历,在前面的张篇blog我们初步实现了链式二叉树递归部分的内容,对于递归算法的学习和思维方式我们仍然需要不断加强,所以将对链式二叉树进行…...

HarmonyOS应用开发者基础认证考试答案
HarmonyOS应用开发者基础认证考试答案 一、判断题 1.Ability是系统调度应用的最小单元,是能够完成一个独立功能的组件。一个应用可以包含一个或多个Ability。 正确(True) 2.所有使用Component修饰的自定义组件都支持onPageShow,onBackPress和onPageHide…...

【前端素材】bootstrap3 实现地产置业公司source网页设计
一、需求分析 地产置业公司的网页通常是该公司的官方网站,旨在向访问者提供相关信息和服务。这些网页通常具有以下功能: 公司介绍:网页通常包含有关公司背景、历史、核心价值观和使命等方面的信息。此部分帮助访问者了解公司的身份和目标。 …...

C++ 数论相关题目 博弈论 Nim游戏
给定 n 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。 问如果两人都采用最优策略,先手是否必胜。 输入格式…...
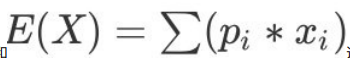
机器学习---无偏估计
1. 如何理解无偏估计 无偏估计:就是我认为所有样本出现的概率⼀样。 假如有N种样本我们认为所有样本出现概率都是 1/N。然后根据这个来计算数学期望。此时的数学期望就是我们平常讲 的平均值。数学期望本质就 是平均值。 2. 无偏估计为何叫做“无偏”࿱…...

C语言基础13
今天是学习嵌入式相关内容的第十四天,以下是今日所学内容 1.结构体: 1.结构体类型定义 2.结构体变量的定义 3.结构体元素的访问 4.结构体的存储 内存对齐 结构体整体的大小必须为最大基本类型长度的整数倍 5.结构体作为函数参数 值传递 练习:定…...

【Java】Maven配置加载到全局
Maven配置加载到全局 <build><plugins><plugin><artifactId>maven-resources-plugin</artifactId><configuration><encoding>utf-8</encoding><useDefaultDelimiters>true</useDefaultDelimiters></configura…...
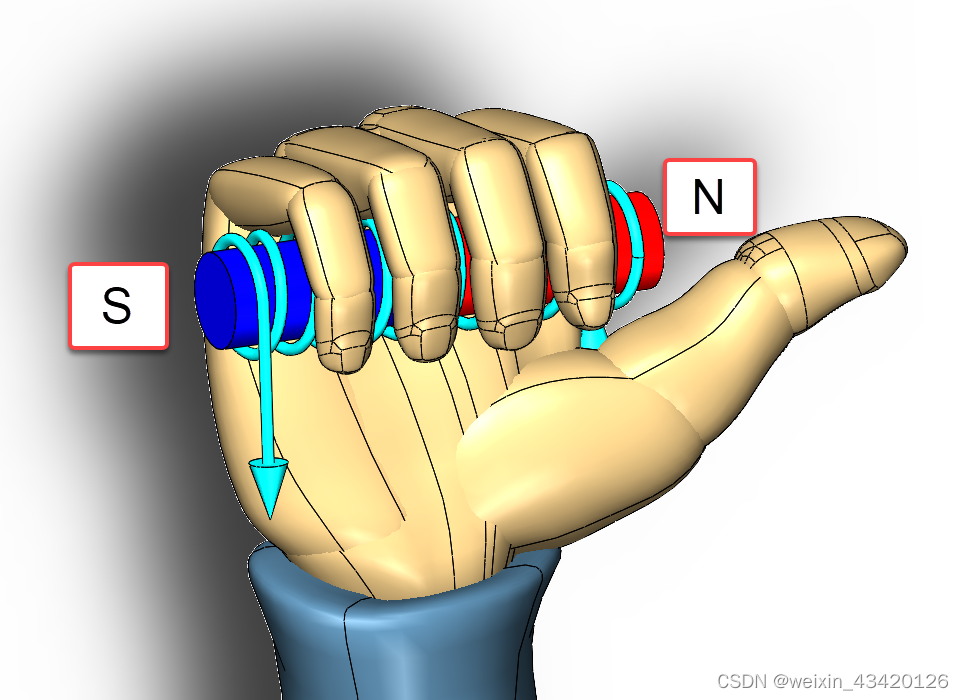
右手螺旋线定则
通电螺线管中的安培定则(安培定则二):用右手握住通电螺线管,让四指指向电流的方向,那么大拇指所指的那一端是通电螺线管的N极。...

2024 高级前端面试题之 React 「精选篇」
该内容主要整理关于 React 模块的相关面试题,其他内容面试题请移步至 「最新最全的前端面试题集锦」 查看。 React模块精选篇 1. 如何理解React State不可变性的原则2. JSX本质3. React合成事件机制4. setState和batchUpdate机制5. 组件渲染和更新过程6. Diff算法相…...
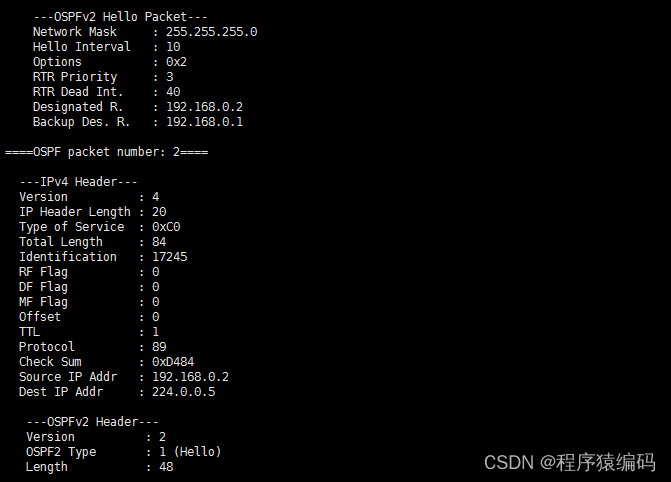
OSPF协议解析及相关技术探索(C/C++代码实现)
OSPF(开放最短路径优先)是一种用于自治系统(AS)内部的路由协议,它是基于链路状态算法的。OSPF的设计目的是为了提供一种可扩展、快速收敛和高效的路由解决方案。 OSPF概念和特点 概念 自治系统(AS&#…...
如何恢复已删除的照片?
在这篇综合文章中发现恢复丢失照片的有效且免费的方法。无论您使用的是智能手机、iPhone、Windows 计算机、Mac、SD 卡还是数码相机,我们都提供有关如何恢复已删除照片的分步说明。此外,学习一些有价值的技巧,以防止将来意外删除照片。 意外…...
VMware虚拟机安装macOS
VMware虚拟机安装macOS 文章目录 VMware虚拟机安装macOS先看效果一、准备工作①:镜像资源下载②:虚拟机③:安装macOS所必要的插件 二、开始安装①:创建新的虚拟机②:自定义硬件③:开启虚拟机 先看效果 一、…...
API管理协作工具:Apipost
相信无论是前端,还是后端的测试和开发人员,都遇到过这样的困难。不同工具之间数据一致性非常困难、低效。多个系统之间数据不一致,导致协作低效、频繁出问题,开发测试人员痛苦不堪。 API管理的难点在哪? 开发人员在 …...
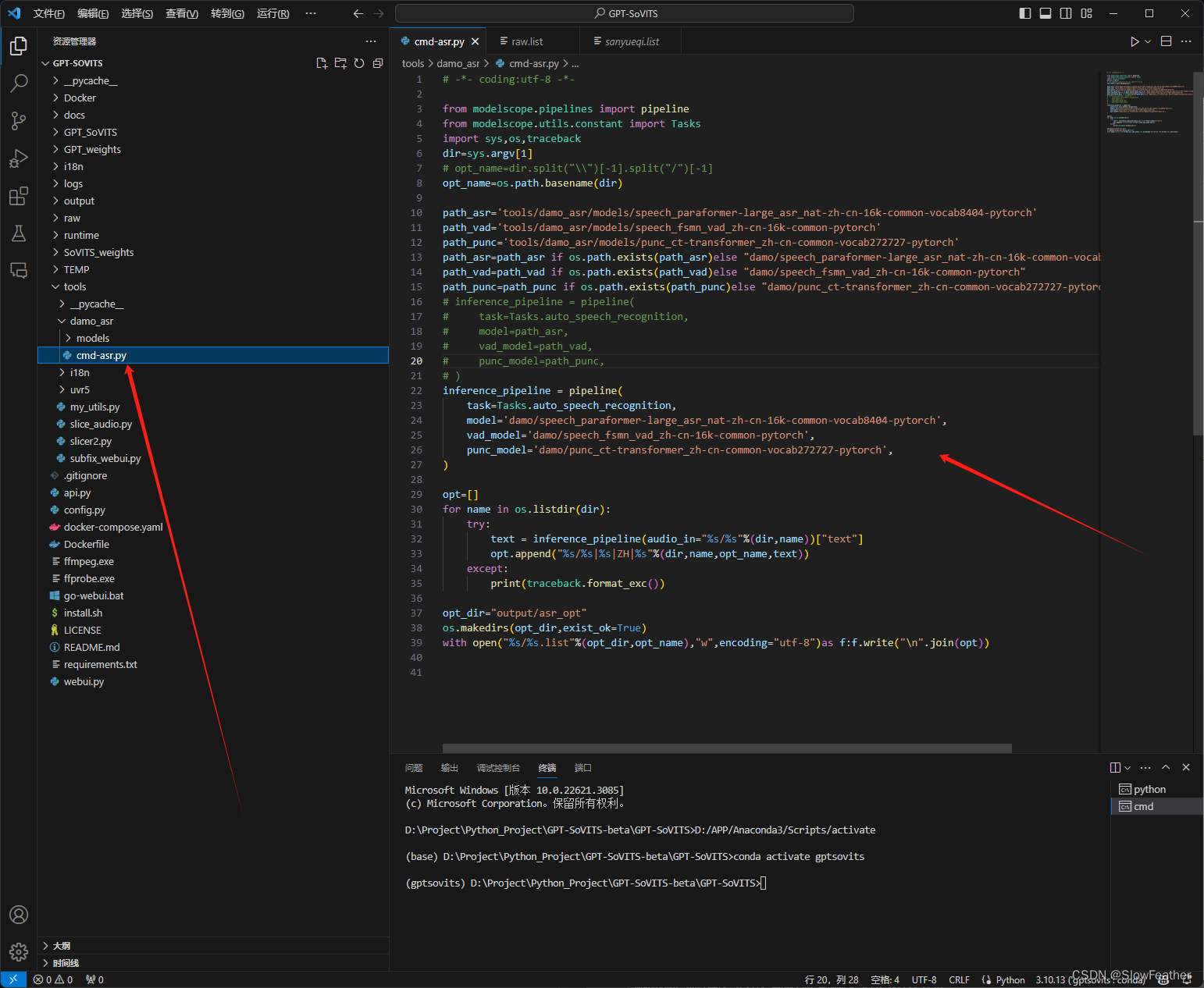
GPT-SoVITS 本地搭建踩坑
GPT-SoVITS 本地搭建踩坑 前言搭建下载解压VSCode打开安装依赖包修改内容1.重新安装版本2.修改文件内容 运行总结 前言 传言GPT-SoVITS作为当前与BertVits2.3并列的TTS大模型,于是本地搭了一个,简单说一下坑。 搭建 下载 到GitHub点击此处下载 http…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
