给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数
这个算法的核心思想是通过交换操作,将每个数放到它应该在的位置上。然后再次遍历数组,找到第一个不在正确位置上的数,其索引加一即为缺失的最小正整数。
def first_missing_positive(nums):n = len(nums)# 第一次遍历,将数组中的每个数放到正确的位置上for i in range(n):while 1 <= nums[i] <= n and nums[nums[i] - 1] != nums[i]:nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]# 第二次遍历,找到第一个不在正确位置上的数,即为缺失的最小正整数for i in range(n):if nums[i] != i + 1:return i + 1# 如果数组中所有数都在正确位置上,则缺失的是数组长度+1return n + 1
这个算法的时间复杂度是 O(n),因为每个数最多进行两次交换操作,而且只进行了两次遍历。额外空间复杂度是 O(1),因为只使用了常数级别的额外空间。
原地哈希算法的原理是通过修改输入数据本身,将数据映射到正确的位置上,从而完成一些特定的操作。在具体的场景中,原地哈希算法通常用于解决一些空间复杂度受限制的问题,以达到在常数级别的额外空间内完成操作的目的。
for i in range(n):while 1 <= nums[i] <= n and nums[nums[i] - 1] != nums[i]:nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]
-
在这一步中,如果 nums[i] 不在正确的位置上,并且它应该在的位置上的数不等于它,就进行交换。
-
第二次遍历:找到第一个不在正确位置上的数,即为缺失的最小正整数。
-
for i in range(n):
if nums[i] != i + 1:
return i + 1
在这一步中,如果 nums[i] 不等于 i + 1,说明 i + 1 是缺失的最小正整数。
这样,通过两次遍历和原地交换的方式,就可以在常数级别的额外空间内找到未排序整数数组中缺失的最小正整数。
原地哈希算法通常涉及到将数据按某种规则重新排列,以满足问题的要求,而不需要额外的数据结构来存储中间结果。
相关文章:

给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数
这个算法的核心思想是通过交换操作,将每个数放到它应该在的位置上。然后再次遍历数组,找到第一个不在正确位置上的数,其索引加一即为缺失的最小正整数。 def first_missing_positive(nums):n len(nums)# 第一次遍历,将数组中的每…...
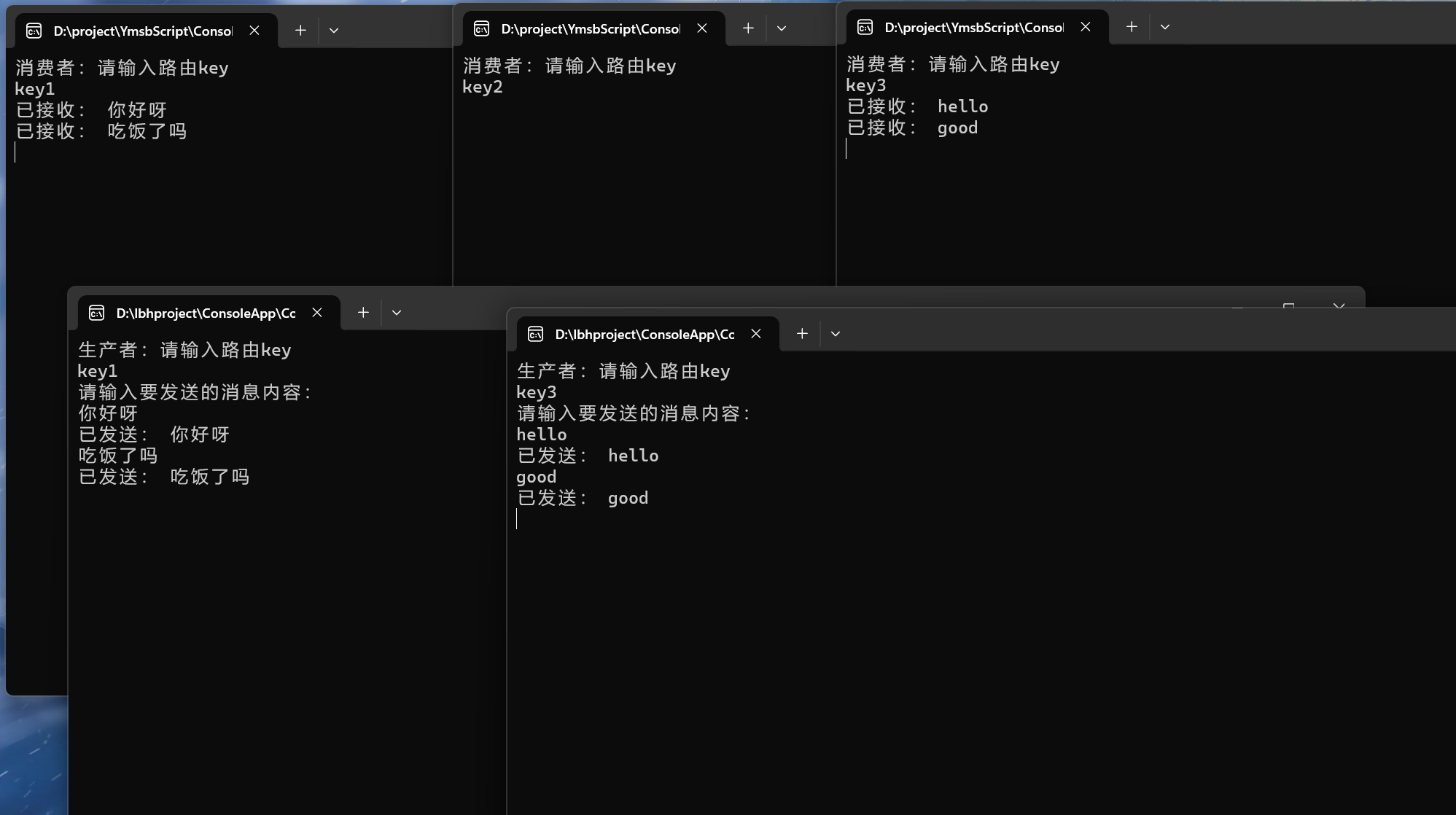
C#使用RabbitMQ-4_路由模式(直连交换机)
简介 RabbitMQ中的路由模式是一种根据Routing Key有条件地将消息筛选后发送给消费者的模式。在路由模式中,生产者向交换机发送消息时,会指定一个Routing Key。交换机接收生产者的消息后,根据消息的Routing Key将其路由到与Routing Key完全匹…...

PyTorch 之 nn.Parameter
文章目录 使用方法:为什么使用 nn.Parameter:示例使用: 在 PyTorch 中,nn.Parameter 是一个类,用于将张量包装成可学习的参数。它是 torch.Tensor 的子类,但被设计成可以被优化器更新的参数。通过将张量包装…...
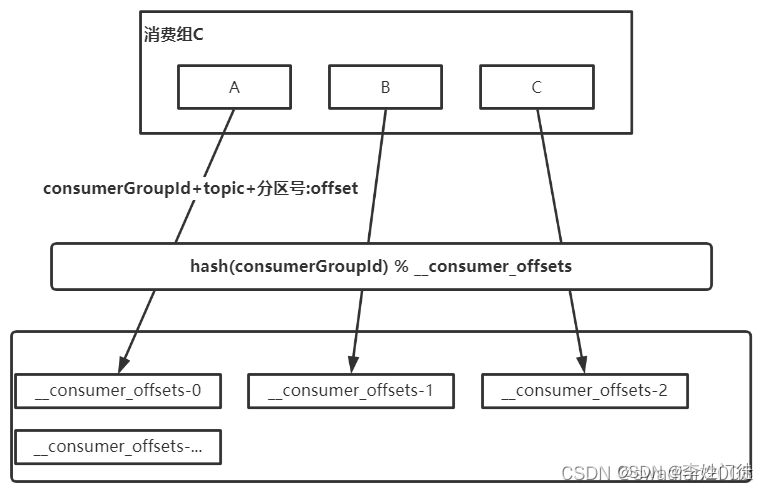
KAFKA高可用架构涉及常用功能整理
KAFKA高可用架构涉及常用功能整理 1. kafka的高可用系统架构和相关组件2. kafka的核心参数2.1 常规配置2.2 特殊优化配置 3. kafka常用命令3.1 常用基础命令3.1.1 创建topic3.1.2 获取集群的topic列表3.1.3 获取集群的topic详情3.1.4 删除集群的topic3.1.5 获取集群的消费组列表…...

3d模型上的材质怎么删除---模大狮模型网
在大多数3D软件中,可以通过以下步骤来删除3D模型上的材质: 选择要删除材质的模型:首先,从场景中选择包含目标材质的模型。可以使用选择工具或按名称查找模型。 进入编辑模式:将模型切换到编辑模式。这通常需要选择相应…...

leetcode hot100跳跃游戏Ⅱ
本题和上一题还是有不一样的地方,这个题中,我们需要记录我们跳跃的步数并尽可能的满足最小的跳跃步数到达终点。 那么我们还是采用覆盖范围的概念,但是我们需要两个,一个是在当前位置的覆盖范围,另一个是下一步的覆盖…...

大数据期望最大化(EM)算法:从理论到实战全解析
文章目录 大数据期望最大化(EM)算法:从理论到实战全解析一、引言概率模型与隐变量极大似然估计(MLE)Jensen不等式 二、基础数学原理条件概率与联合概率似然函数Kullback-Leibler散度贝叶斯推断 三、EM算法的核心思想期…...
【鸿蒙】大模型对话应用(二):对话界面设计与实现
Demo介绍 本demo对接阿里云和百度的大模型API,实现一个简单的对话应用。 DecEco Studio版本:DevEco Studio 3.1.1 Release HarmonyOS SDK版本:API9 关键点:ArkTS、ArkUI、UIAbility、网络http请求、列表布局、层叠布局 对话页…...

MySQL 导入数据
我们可以将已有的数据导入到MySQL数据库中,下面是几种方式: 1、mysql 命令导入 使用 mysql 命令导入语法格式为: mysql -u用户名 -p密码 < 要导入的数据库数据(shulanxt.sql) 实例: # mysql -uroot -p123456 < …...

探索数字经济:从基础到前沿的奇妙旅程
新一轮技术革命方兴未艾,特别是以人工智能、大数据、物联网等为代表的数字技术革命,催生了一系列新技术、新产业、新模式,深刻改变着世界经济面貌。数字经济已成为重组全球要素资源、重塑全球经济结构、改变全球竞争格局的关键力量。预估到20…...
】如何在 Windows 操作系统上设置 Design Space Explorer II 远程 SSH 场)
【INTEL(ALTERA)】如何在 Windows 操作系统上设置 Design Space Explorer II 远程 SSH 场
说明 从英特尔 Quartus Prime Pro Edition 软件 22.1 版本开始,您可以选择使用 Windows OpenSSH 服务器设置 Design Space Explorer II (DSE II)。 解决方法 1.让 DSE II 与 OpenSSH 协同工作的第一步是 安装 OpenSSH。应在远程主机上安装 Op…...

Python编程-使用urllib进行网络爬虫常用内容梳理
Python编程-使用urllib进行网络爬虫常用内容梳理 使用urllib库进行基础网络请求 使用request发起网络请求 from urllib import request from http.client import HTTPResponseresponse: HTTPResponse request.urlopen(url"http://pkc/vul/sqli/sqli_str.php") pr…...
01 Redis的特性+下载安装启动+Redis自动启动+客户端连接
1.1 NoSQL NoSQL(“non-relational”, “Not Only SQL”),泛指非关系型的数据库。 键值存储数据库 : 就像 Map 一样的 key-value 对。如Redis文档数据库 : NoSQL 与关系型数据的结合,最像关系…...

C++发起Https请求
Wininet库忽略Https证书 相信很多朋友使用C WINAPI开发的时候网络模块的时候遇到Https忽悠证书无效的情况下, 仍然希望获取结果下列代码便是忽略异常的Https CA证书,下面对原理进行简单的讲解首先, 需要设置Https忽略需要用到如下结果函数与参数Interne…...
哪款笔记软件支持电脑和手机互通数据?
上班族在日常工作中,随手记录工作笔记已成为司空见惯的场景。例如:从快节奏的会议记录到灵感迸发的创意;跟踪项目进展,记录每个阶段的成果、问题和下一步计划;记录、更新工作任务清单等,工作笔记承载了职场…...
部署PXE高效批量网络装机
部署PXE高效批量网络装机 因在Cisco3850核心交换机中已开启DHCP 服务,因此不需要在配置DHCP服务。如果您的网络环境中也已有DHCP服务,也不用再配置DHCP服务了,直接部署PXE相关服务即可。 找一台linux系统的服务器,这本次试验用的是…...
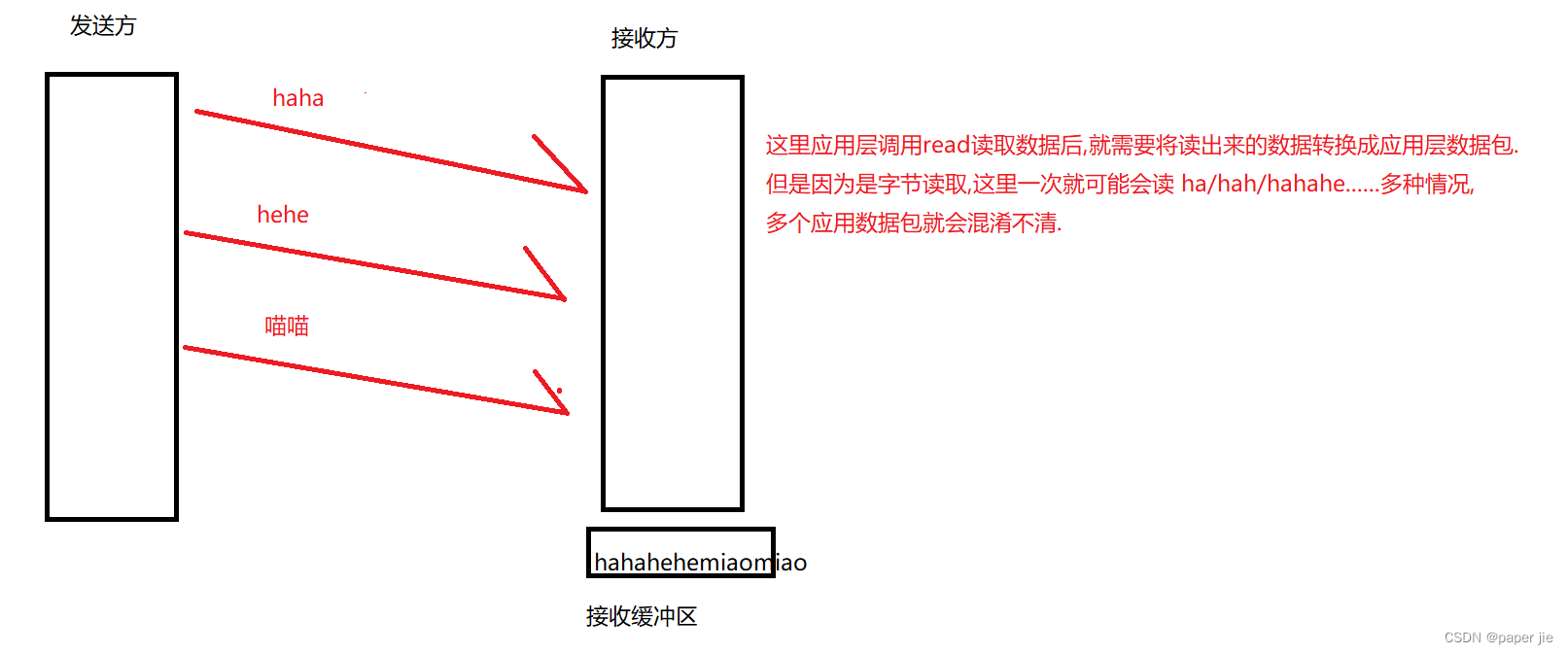
【JavaEE】UDP协议与TCP协议
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文于《JavaEE》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&…...

Leetcode—1828. 统计一个圆中点的数目【中等】
2024每日刷题(一零五) Leetcode—1828. 统计一个圆中点的数目 实现代码 class Solution { public:vector<int> countPoints(vector<vector<int>>& points, vector<vector<int>>& queries) {vector<int> a…...
)
新概念英语第二册(47)
New words and expressions】生词和短语(9) thirsty adj. 贪杯的 ghost n. 鬼魂 haunt v. (鬼)来访,闹鬼 block …...
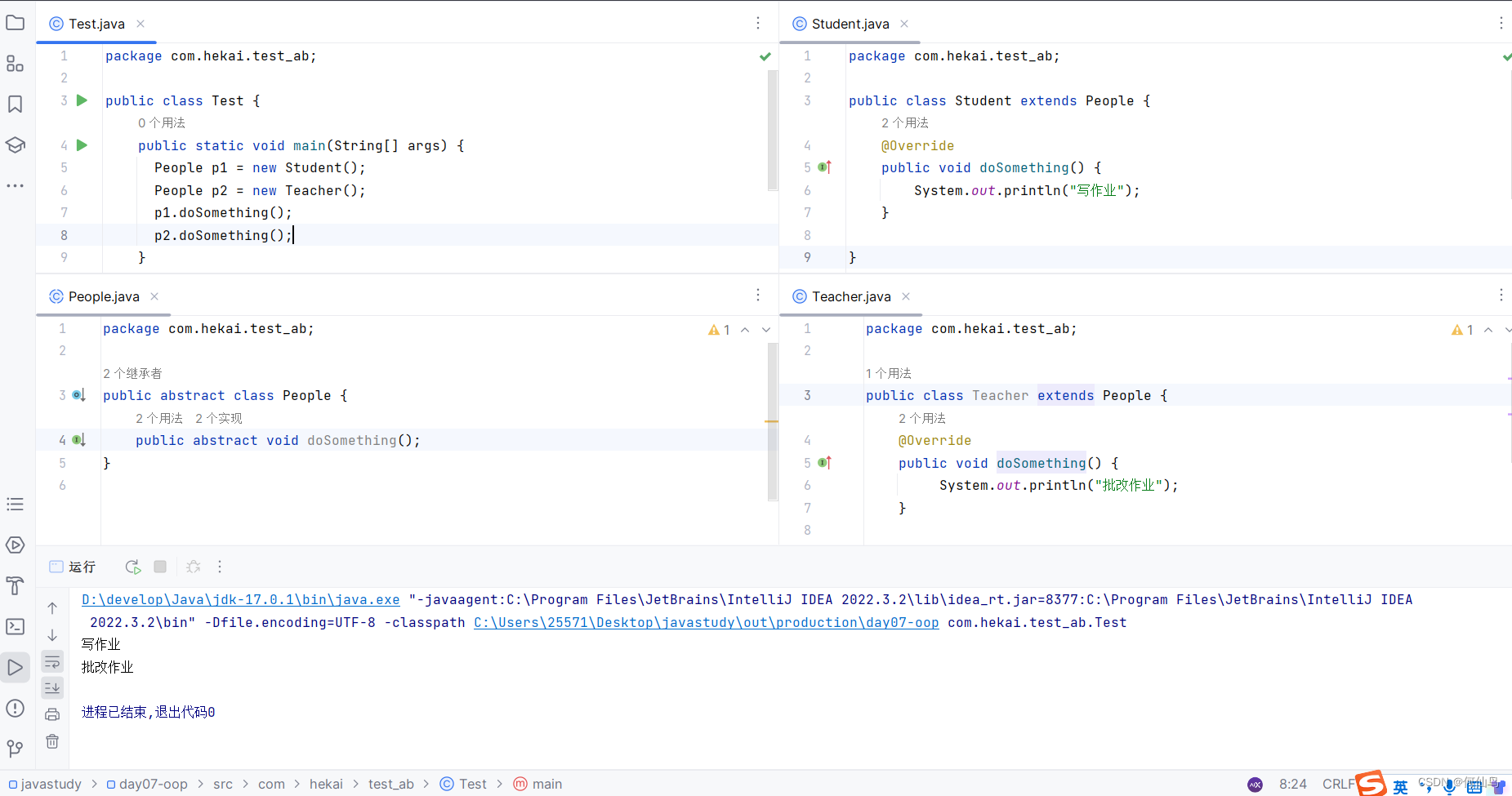
抽象类(Java)、模板方法设计模式
一、概念 在Java中有abstract关键字,就是抽象的意思,可用来修饰类和成员方法。 用abstract来修饰类,那这个类就是抽象类;修饰方法,那这个方法就是抽象方法。 修饰符 abstract class 类名{修饰符 abstract 返回值类型…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
