【数据结构】(三)树Tree

目录
1、基本概念
2、二叉树Binary Tree
3、树、森林与二叉树的转换
4、赫夫曼树Huffman Tree与赫夫曼编码Huffman Coding
1、基本概念
(1)树(Tree)是 n(n ≥\geq 1)个节点的有限集,n = 0时称为空树。
(2)非空树唯一拥有一个根(Root)结点(Node),n > 1时其余结点可分为m(m > 0)个互不相交的有限集并各自成根的子树(Sub Tree)。
(3)结点拥有的子树数目称为结点的度(Degree),度为 0 的结点称为叶结点(Leaf),树的度是树各结点的度的最大值。

(4)结点之间的关系:兄弟(Sibling)——孩子(Child)——双亲(Parent)

(5)结点的层次(Level)从根算起,根为第一层,根的孩子为第二层一直往下,最大层次为深度(Depth)。

(6)如果将树中结点的各子树看成从左至右呈有次序的不能互换的,则称该树为有序树,否则称为无序树。
(7)森林(Forest)是 m(m ≥\geq 0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。
(8)树的双亲表示法如下,data数据域存储结点的数据信息;parent指针域存储该结点双亲在数组中的下标,根结点的parent定义为 -1 即不存在该结点。

2、二叉树Binary Tree
(1)每个结点的度 ≤\leq 2,左右有次序之分的树称为二叉树。
(2)二叉树的五种基本形态:空二叉树、只有一个根结点、根结点只有左子树、根结点只有右子树、根结点既有左子树又有右子树。
(3)斜树包含左斜树(所有结点都只有左子树的二叉树)和右斜树(所有结点都只有右子树的二叉树),每一层都只有一个结点,结点个数即二叉斜树的深度(同线性表结构)。
(4)满二叉树:叶结点仅在最下层,非叶非根的结点度数均为 2 的二叉树。

满二叉树
(5)完全二叉树:按层序从上到下从左到右编号结点的位置与满二叉树相同的二叉树,特点有叶结点仅在最下两层,最下层叶子集中在左部连续位置,同结点数的二叉树深度最小。

完全二叉树
(6)二叉树的数学性质有:
(i) 第 i 层至多 2i−12^{i-1} 个结点(i ≥\geq 1)
(ii) 深度为k时至多有 2k2^{k} -1个结点(k ≥\geq1)
(iii) 所有节点的度数之和等于节点总数-1,若叶子结点数为 n0n_{0} ,度为2的结点数为n1n_{1} ,则n0n_{0} = n1n_{1} + 1( 二叉树除了叶结点就是度为1或2的结点)
(iv) 具有n个结点的完全二叉树的深度为[logn]+1
(7)顺序存储结构:一般只用于完全二叉树。
(8)二叉链表:一个数据域+两个指针域。
(9)遍历二叉树:从根节点出发,按某种次序依次唯一地访问每个结点。
(i) 前序遍历:若二叉树为空,则空操作返回,否则先访问根结点,然后遍历左子树, 再遍历右子树。
(i) 中序遍历:若二叉树为空,则空操作返回,否则先遍历左子树,然后访问根结点,再遍历右子树。
(i) 后序遍历:若二叉树为空,则空操作返回,否则从左到右先叶子后结点遍历访问左右子树,最后根结点。

(i) 层序遍历:若二叉树为空,则空操作返回,否则从第一层根结点开始往下从左到右对结点逐个访问。
已知前 + 中序 / 中 + 后序遍历序列,都可以唯一确定一棵二叉树。
3、树、森林与二叉树的转换
(1)树转换为二叉树
(i) 加线;在所有兄弟结点之间加一条连线。
(ii) 去线;每个结点只保留它与第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
(iii) 层次调整:以树的根结点为轴心,将整棵树顺时针旋转一定角度使其结构层次分明。

(2)森林转二叉树
(i) 将每棵树转换为二叉树。
(ii) 第一棵二叉树不动,从第二棵开始依次把后一棵二叉树的根结点作为前一棵根结点的右孩子,连线。

(3)二叉树转换成树
(i) 加线;左孩子的n个右孩子结点都作为此结点的孩子。将该结点与这些右孩子结点用线连接起来。
(ii) 去线;删除原二叉树中所有结点与其右孩子结点的连线。

(4)二叉树转森林
(i) 从根结点开始,若存在右孩子,则删除与右孩子的连线。
(ii) 再查看分离后的二叉树,若存在右孩子,则连线删除,直到所有右孩子连线删除为止。
(iii) 再将分离的二叉树都转换为树即可。

4、赫夫曼树Huffman Tree与赫夫曼编码Huffman Coding
从树一个结点到另一个结点的之间的分支构成两个结点之间的路径,路径分支数目称为路径长度。树的路径长度即从树根到每一结点的路径长度之和,结点间连线相关数称为权(Weight)。树的带权路径长度为树中所有叶子结点的带权路径长度之和,带权路径长度WPL最小的二叉树称为赫夫曼树。

二叉树a的路径长度为1+1+2+2+3+3+4+4=20,WPL = 5×\times1 + 15×\times2 + 40×\times3 + 30×\times4 + 10×\times4 = 315
二叉树b的路径长度为1+2+3+3+2+1+2+2=16,WPL = 5×\times3 +15×\times3 + 40×\times2 + 30×\times2 + 10×\times4 = 220
我们可以得出构造赫夫曼树的算法描述:
(1)根据给定的n个权值{ w1w_{1},w2w_{2},w3w_{3}……,wnw_{n}},构成 n 棵二叉树的集合F={ T1T_{1},T2T_{2},T3T_{3}……,TnT_{n}},其中每棵二叉树T中只有一个带权为w的根结点,其左右子树均为空。
(2)在 F 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,并置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
(3)在 F 中删除这两棵树,同时将新得到的二叉树加入F中。
(4)重复步骤(2)和(3)直到F只含一棵树为止,这棵树便是赫夫曼树。
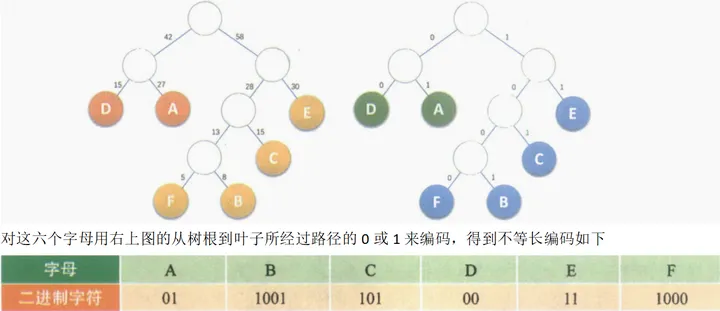
赫夫曼编码:规定赫夫曼树的左分支代表0,右分支代表1,则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码,即赫夫曼编码,它在信息存储与传输过程中对信息高效压缩。
假设六个字母的频率为A 27,B 8,C 15,D 15,E 30,F 5,合起来正好是100%,赫夫曼树构造如下:
相关文章:

【数据结构】(三)树Tree
目录 1、基本概念 2、二叉树Binary Tree 3、树、森林与二叉树的转换 4、赫夫曼树Huffman Tree与赫夫曼编码Huffman Coding 1、基本概念 (1)树(Tree)是 n(n ≥\geq 1)个节点的有限集,n 0时称…...

扩展坞 接两个显示器
笔记本电脑如何外接两个显示器,达到三个屏同时显示? 3 笔记本有 2 个显示扩展接口 目前笔记本中最常见的就是 1 个 HDMI 口 1 个支持 DP 协议的 Type-C 口或 2 个支持 DP 协议的 Type-C 口,此时使用 HDMI 线和 Type-C 转接线分别直连两台显…...

鸿蒙 ArkTS 从数组内查找指定的数据
let arr [1, 2, 3, 4, 5]; let target 3; let result arr.filter(item > item target); let a String(result) 将数字转换成文本型 console.log(a); 亲爱的读者: 首先,我要感谢您抽出宝贵的时间阅读这篇文章。我深知,您的每一分每一…...
qemu 抓取linux kernel vmcore
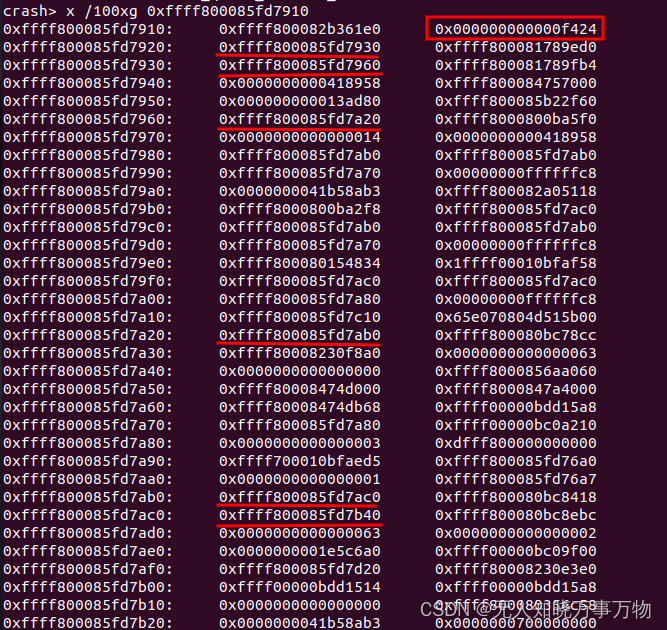
一、背景 在qemu调试linux kernel时 有时我们会遇到dump 情况,这时可以通过gdb 方式连接分析dump, 但实际中我们用得更多的是离线dump 分析,分析的文件通常是vmcore(linux kernel panic 生成的coredump文件)或者ramdu…...

RabbitMQ 死信队列应用
1. 概念 死信队列(Dead Letter Queue)是在消息队列系统中的一种特殊队列,用于存储无法被消费的消息。消息可能会因为多种原因变成“死信”,例如消息过期、消息被拒绝、消息队列长度超过限制等。当消息变成“死信”时,…...

除毛可以用宠物空气净化器吗?猫用空气净化器哪些品牌吸毛好?
作为一位长期养猫的铲屎官,我深刻理解只有养猫人才懂的困扰,那就是家里到处都是猫毛和异味。我发现自从开始养猫之后,家里的空气质量变得不佳。猫毛和皮屑飞扬,而且室内空气中的污染物也越来越多。这种低质量的空气对我们的健康有…...

有趣的css - 好看的呼吸灯效果
整体效果 这个效果主要用 css3 的 animation 属性来实现的。 这个效果可以用作在网站的整体 Loading,也可以放在网站首屏当一个 banner 的背景也是非常棒的! 代码部分 html 部分代码: <div class"app"><span class&quo…...
二叉树-堆应用(1)
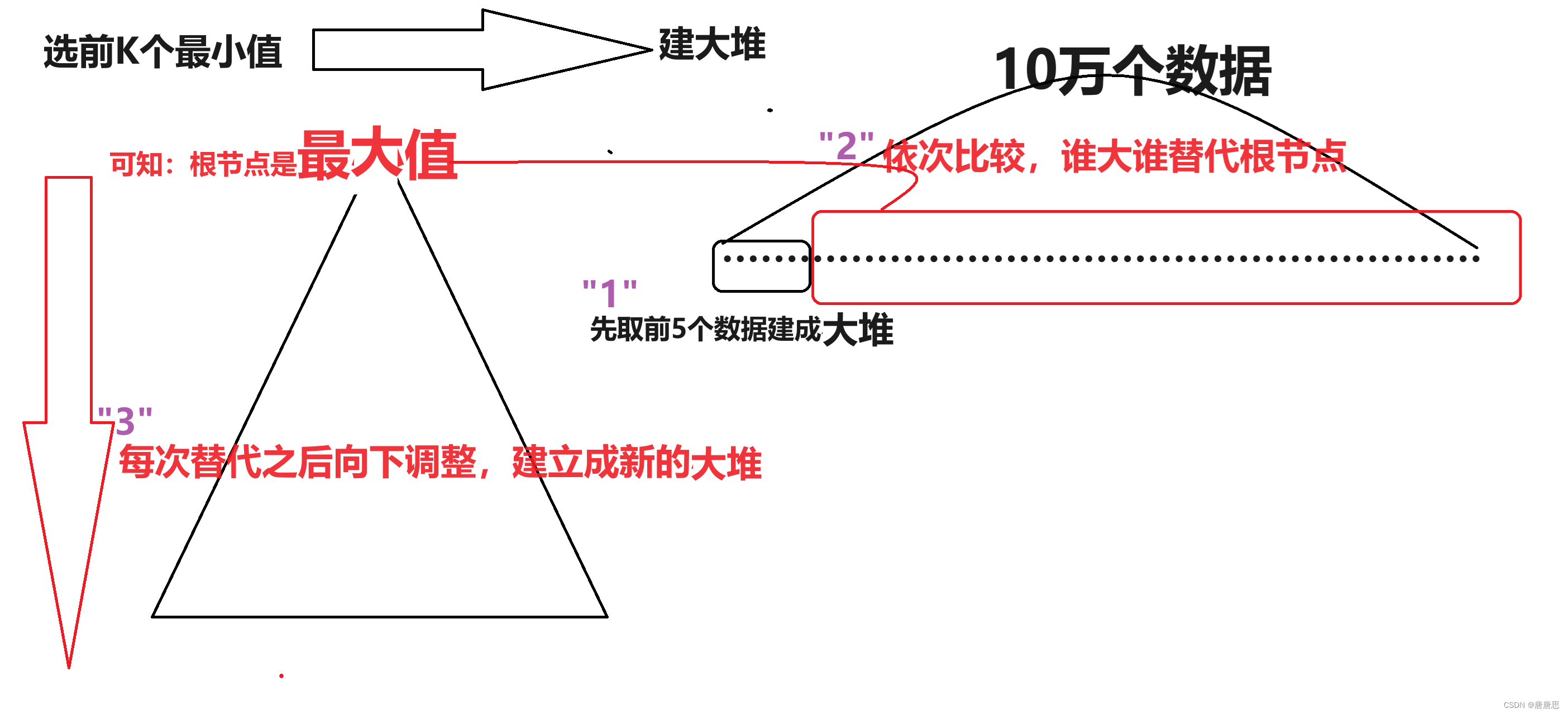
目录 堆排序 整体思路 代码实现 Q1建大堆/小堆 Q2数据个数和下标 TopK问题 整体思路 代码实现 Q1造数据CreateData Q2建大堆/小堆 建堆的两种方法这里会用到前面的向上/向下调整/交换函数。向上调整&向下调整算法-CSDN博客 堆排序 整体思路 建堆(直…...

猫头虎博主第10期赠书活动:《写给大家看的Midjourney设计书》
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通Golang》…...

线程池相关的类学习
Executor public interface Executor {//执行任务void execute(Runnable command); }ExecutorService public interface ExecutorService extends Executor {//关闭线程池,不能再向线程池中提交任务,已存在与线程池中的任务会继续执行,直到…...
Redis核心技术与实战【学习笔记】 - 9.如何避免单线程模型的阻塞
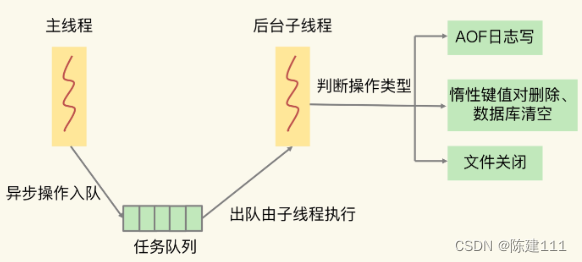
概述 Redis 被广泛应用的原因是因为它支持高性能访问。所以,我们要重视所有可能影响 Redis 性能的因素(如命令操作、系统配置、关键机制、硬件配置等)。 影响 Redis 性能的 5 大方面的潜在因素分别是: Redis 内部的阻塞式操作C…...
 迭代数组)
如何在 JavaScript 中使用 map() 迭代数组
简介 从经典的 for 循环到 forEach() 方法,JavaScript 中有各种技术和方法用于遍历数据集。其中最流行的方法之一是 .map() 方法。.map() 通过在父数组的每个项目上调用特定函数来创建一个数组。.map() 是一个非变异方法,它创建一个新数组,而…...

学习JavaEE的日子 Day19 常用类
Day19 1.包装类的使用 理解:8种基本数据类型对应类 出现原因: Java为纯面向对象语言(万物皆对象),8种基本数据类型不能new对象, 就破坏Java为纯面向对应语言的特征,Java又为8种基本数据类型分别 匹配了对应的…...
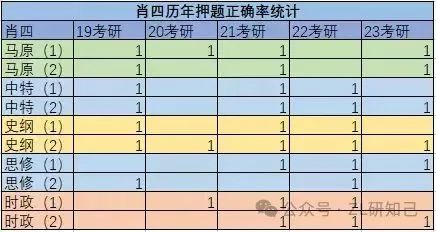
25考研政治备考计划
各位小伙伴大家好,今天给大家分享的是25考研政治复习备考计划。 政治没有基础阶段,直接就是强化,强化的内容也就是听课,刷题。 【时间安排】 *7-9月中 徐涛老师或腿姐强化课,推荐刷肖1000 *9月中-10月中 背腿姐的背…...

漏洞01-目录遍历漏洞/敏感信息泄露/URL重定向
目录遍历漏洞/敏感信息泄露/URL重定向 文章目录 目录遍历敏感信息泄露URL重定向 目录遍历 敏感信息泄露 于后台人员的疏忽或者不当的设计,导致不应该被前端用户看到的数据被轻易的访问到。 比如: ---通过访问url下的目录,可以直接列出目录下…...
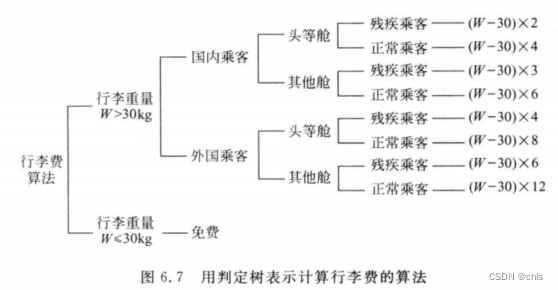
软件工程知识梳理4-详细设计
详细设计阶段的根本目标是确定应该怎样具体地实现所要求的系统,也就是说.经过这个阶段的设计工作.应该得出对目标系统的精确描述.从而在编码阶段可以把这个描述直接翻译成用某种程序设计语言书写的程序。 详细设计的的目标不仅仅是逻辑上正确地实现每个模块地功能&a…...

Spring Boot3,启动时间缩短 10 倍!
前面松哥写了一篇文章和大家聊了 Spring6 中引入的新玩意 AOT(见Spring Boot3 新玩法,AOT 优化!)。 文章发出来之后,有小伙伴问松哥有没有做性能比较,老实说,这个给落下了,所以今天…...
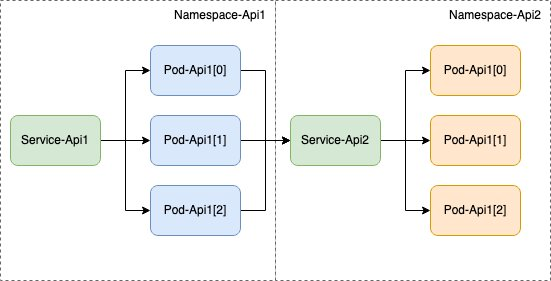
Picturesocial | 只要 5 分钟,发现容器编排的秘密武器!
在上一篇文章《Picturesocial | 开发实践:如何在 15 分钟内将应用容器化》,我们讨论了容器以及容器化应用程序所需的步骤。在不考虑将 container 部署到哪里的情况下创建 container,就像把家放在漂浮在海中的货运集装箱里一样,听起…...

GEE数据集——Umbra 卫星合成孔径雷达开放数据
Umbra 合成孔径雷达开放数据 Umbra 卫星生成的合成孔径雷达图像分辨率最高(优于 25 厘米/10 英寸)。合成孔径雷达卫星可以在夜间、透过云层、烟雾和雨水捕捉图像。合成孔径雷达具有监测变化的独特能力。开放数据计划(ODP)对全球十个不同地点进行监测。经常更新新图像。ODP …...

一个vue项目中通过iframe嵌套另外一个vue项目,如何让这两个项目进行通信
文章目录 需求分析父传子子传父 需求 一个vue项目中通过iframe嵌套另外一个vue项目,如何让这两个项目之间进行通信 分析 在Vue项目中通过iframe嵌套另外一个Vue项目时,可以通过postMessage方法实现这两个项目之间的通信。postMessage是HTML5新增加的API…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
