【leetcode100-081到090】【动态规划】一维五题合集1
【爬楼梯】
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
思路:
-
【状态】
dp[i];//爬i级台阶有几种方法
-
【初始】
dp[0] = 1;//爬0级1种(不爬)dp[1] = 1;//爬1级1种
-
【递推】
dp[i] = dp[i-2] + dp[i-1];//爬i级=先爬i-1级再爬1级+先爬i-2级再爬2级,没有其他可能了
-
【结论】
dp[n];//爬n级方法数
class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1);dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};【杨辉三角】
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
思路:
观察示例可以发现:
每一行的行号也是该行元素的最大下标;
每行的首尾元素是1;
其余元素是它左上和右上元素的和;
把以上规则翻译成代码语言即可。
class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> ans;vector<int> lastRow(1,1);ans.push_back(lastRow);if (numRows == 1)return ans;for (int i = 1; i < numRows; i++) {vector<int> curRow;//当前行最大下标就是icurRow.push_back(1);for (int j = 1; j < i; j++) {curRow.push_back(lastRow[j - 1] + lastRow[j]);}curRow.push_back(1);ans.push_back(curRow);lastRow.resize(i+1);lastRow = curRow;}return ans;}
};【打家劫舍】
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
思路:
建立dp数组,dp[i]代表到房子i为止最高可以偷到的金额。
对当前房子,我们分别计算偷它和不偷它可以获得的最大金额,并记录两者中较大的那个:
偷它,那么i-1号房子不可以偷,总金额是,偷i-2及以前的房子+偷i;
不偷它,那么i-1房子可以偷,总金额就是偷i-1及以前的房子;
class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();if (n == 1)return nums[0];vector<int> dp(n, 0);dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for (int i = 2; i < n; i++) {dp[i] = max(nums[i] + dp[i - 2], dp[i - 1]);}return dp[n - 1];}
};【完全平方数】
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
思路:
本题从如何减小问题规模入手。
首先,对拿到的数,我们已经知道任意一个比它小的数最少由几个完全平方数组成;
因此,我们可以先从当前数字中减掉一个完全平方数,然后通过dp直接拿到剩下的数的dp值,此时,这种切分方式得到的答案就是该dp值+1;
对当前数字,能从中减掉的完全平方数可能不止一个,因此,我们应该把能减的平方数全都试一遍,并把所有答案中最小的那个设为当前数字的dp值。
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1);dp[0] = 0;//填数组for (int k = 1; k <= n; k++) {int curMin = INT_MAX;//枚举平方根以下的数for (int i = 1; i * i <= k; i++) {curMin = min(curMin, dp[k - i * i]);}dp[k] = curMin + 1;}return dp[n];}
};【零钱兑换】
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
思路:
和上一题本质上没有任何区别,只要把上一题枚举的“完全平方数”在这题改成“硬币面值”,就完事儿了。
class Solution {
public:int coinChange(vector<int>& coins, int amount) {int n = coins.size();sort(coins.begin(), coins.end());if (amount == 0)return 0;if (amount < coins[0])return -1;vector<int> dp(amount + 1);dp[0] = 0;//依次计算for (int i = 1; i <= amount; i++) {int curMin = INT_MAX;//记录当前金额能否凑成bool flag = false;// calculate dp[i]//枚举比总数小的所有硬币面值for (int j = 0; j < n && 0 <= i - coins[j]; j++) {//如果去掉当前面值以后能凑出来if (dp[i - coins[j]] != -1) {//记录最少数量curMin = min(curMin, dp[i - coins[j]] + 1);//记录可以凑出flag = true;}}dp[i] = flag ? curMin : -1;}return dp[amount];}
};相关文章:

【leetcode100-081到090】【动态规划】一维五题合集1
【爬楼梯】 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 思路: 【状态】 dp[i];//爬i级台阶有几种方法 【初始】 dp[0] 1;//爬0级1种(不爬)dp[1] 1;/…...

数据结构-顺序表详解专题
目录 顺序表 1.简单了解顺序表 2.顺序表的分类 2.1静态顺序表 2.2动态顺序表 2.3typedef命名作用 3.动态顺序表的实现 SeqList.h SeqList.c test.c 顺序表 1.简单了解顺序表 顺序表是线性表的一种,线性表是在逻辑上是线性结构,在物理逻辑上并…...

对商业知识和思维的一些小体会
用途:个人学习笔录,欢迎指正 前言: 小生拙见,我认为商业知识和商业思维的理解对于每一个行业都有潜在的帮助,因为每个人的生活都离不开商业,生意、工作都是交换,用自身提供的价值换取薪酬。因此…...

【笔记】计算文件夹的大小
目标:遍历文件夹,计算文件夹下包含文件和文件夹的大小。将这些结果存入python自带的数据库。 用大模型帮我设计并实现。 Step1 创建一个测试用的目录结构 创建目录结构如下所示: TestDirectory/ │ ├── EmptyFolder/ │ ├── SmallF…...
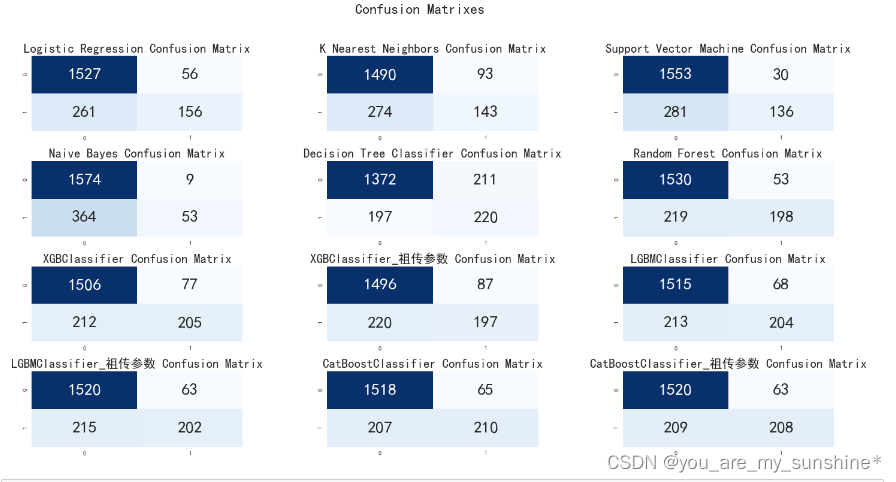
机器学习_常见算法比较模型效果(LR、KNN、SVM、NB、DT、RF、XGB、LGB、CAT)
文章目录 KNNSVM朴素贝叶斯决策树随机森林 KNN “近朱者赤,近墨者黑”可以说是 KNN 的工作原理。 整个计算过程分为三步: 计算待分类物体与其他物体之间的距离;统计距离最近的 K 个邻居;对于 K 个最近的邻居,它们属于…...

外包干了8个月,技术退步明显...
先说一下自己的情况,大专生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四年的功能测…...
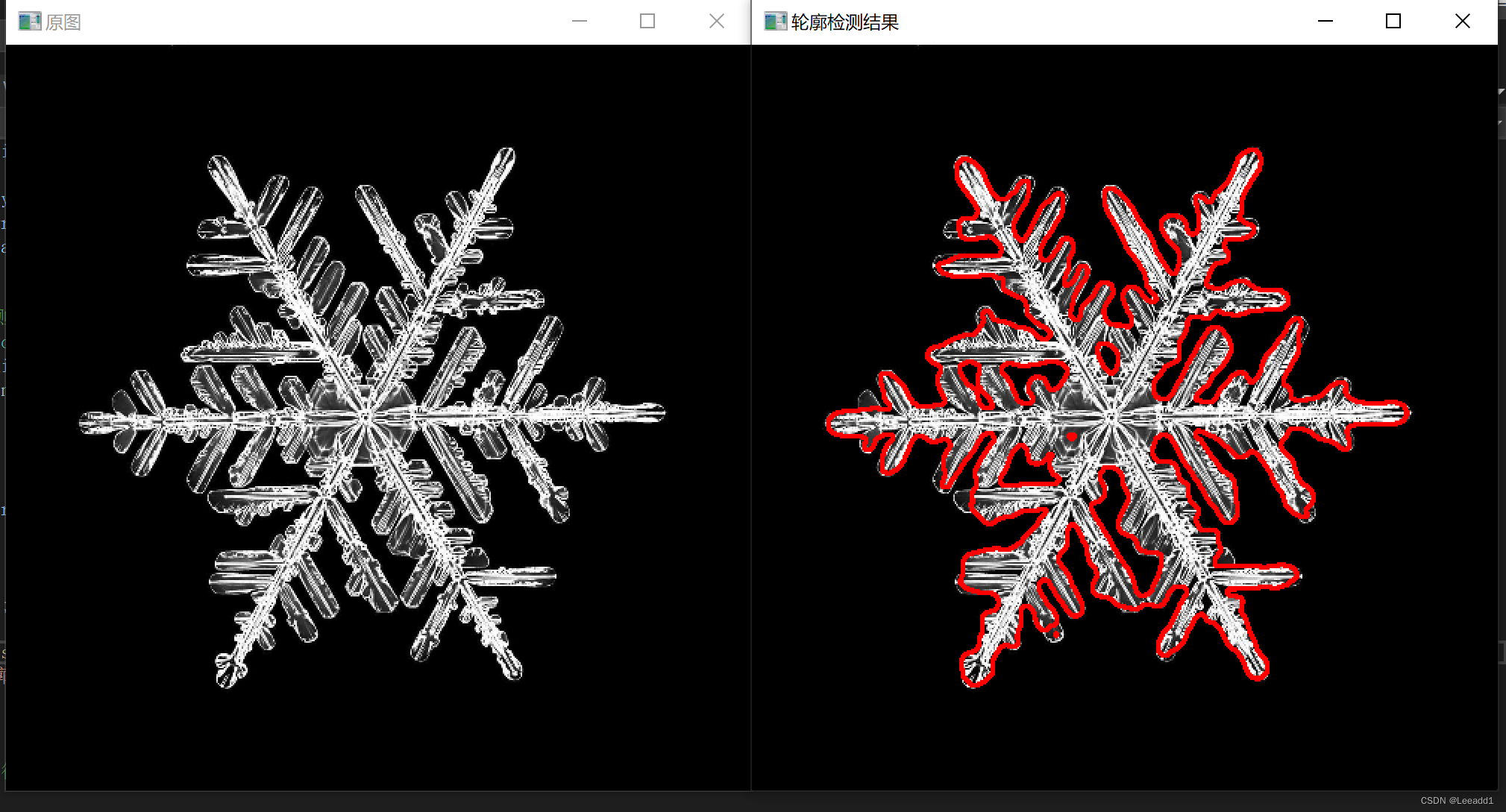
opencv#41 轮廓检测
轮廓概念介绍 通常我们使用二值化的图像进行轮廓检测,对轮廓以外到内进行数字命名,如下图,最外面的轮廓命名为0,向内部进行扩展,遇到黑色白色相交区域,就是一个新的轮廓,然后依次对轮廓进行编号…...
Websocket基本用法
1.Websocket介绍 WebSocket是基于TCP的一种新的网络协议。它实现了浏览器与服务器全双工通信——浏览器和服务器只需要完成一次握手,两者之间就可以创建持久性的连接,并进行双向数据传输。 应用场景: 视频弹幕网页聊天体育实况更新股票基金…...
node.js与express.js创建项目以及连接数据库
搭建项目 一、技术准备 node版本:16.16.0 二、安装node成功后,安装express,命令如下: npm install -g express 或者: npm install --locationglobal express 再安装express的命令工具: npm install --location…...

【Tomcat与网络8】从源码看Tomcat的层次结构
在前面我们介绍了如何通过源码来启动Tomcat,本文我们就来看一下Tomcat是如何一步步启动的,以及在启动过程中,不同的组件是如何加载的。 一般,我们可以通过 Tomcat 的 /bin 目录下的脚本 startup.sh 来启动 Tomcat,如果…...

Java Agent Premain Agentmain
概念 premain是在jvm启动的时候类加载到虚拟机之前执行的 agentmain是可以在jvm启动后类已经加载到jvm中了,才去转换类。 这种方式会转换会有一些限制,比如不能增加或移除字段。 具体的做法,两者的实际做法是差不多的: premain 定义个静…...

Python实现设计模式-策略模式
策略模式是一种行为型设计模式,它定义了一系列算法或策略,并将它们封装成独立的类,使得它们可以相互替换,而不影响客户端的使用。 在策略模式中,算法或策略被封装在单独的策略类中,这些策略类实现了相同的…...
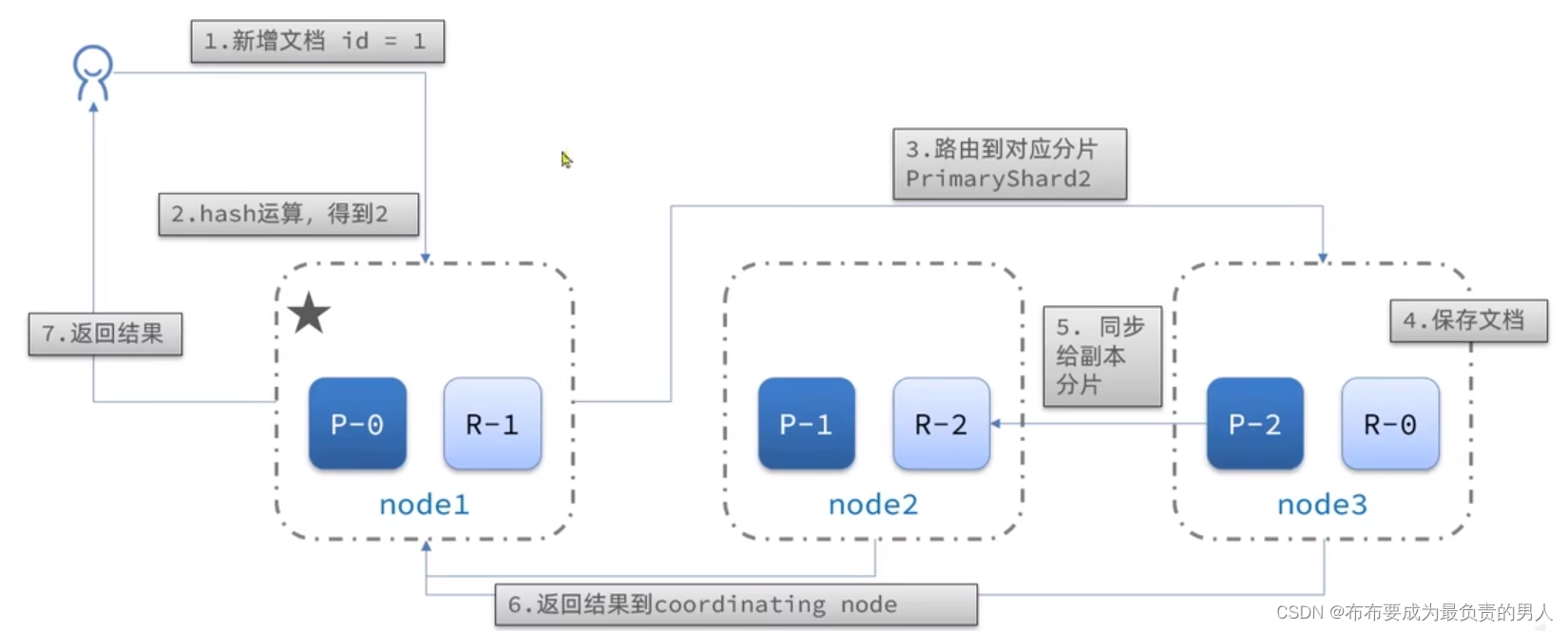
详解SpringCloud微服务技术栈:深入ElasticSearch(4)——ES集群
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:详解SpringCloud微服务技术栈:深入ElasticSearch(3)——数据同步(酒店管理项目&a…...
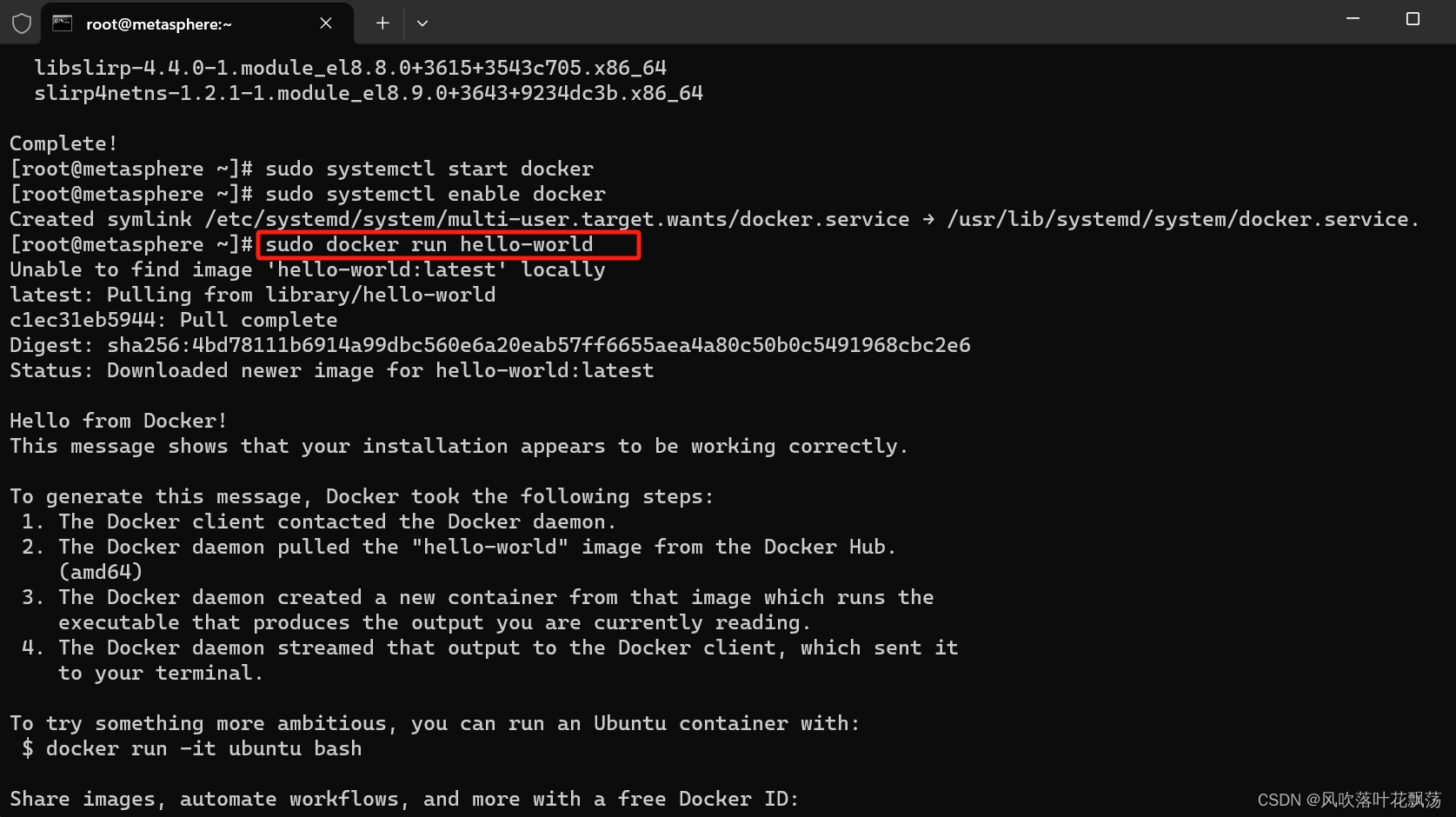
AlmaLinux上安装Docker
AlmaLinux上安装Docker 文章目录 AlmaLinux上安装Docker一、前言二、具体步骤1、Docker 下载更新系统包索引:添加Docker仓库:安装Docker引擎: 2、Docker服务启动启动Docker服务:设置Docker开机自启: 3、Docker 安装验证…...

熟悉MATLAB 环境
一、问题描述 熟悉MATLAB 环境。 二、实验目的 了解Matlab 的主要功能,熟悉Matlab 命令窗口及文件管理,Matlab 帮助系统。掌握命令行的输入及编辑,用户目录及搜索路径的配置。了解Matlab 数据的特点,熟悉Matlab 变量的命名规则&a…...
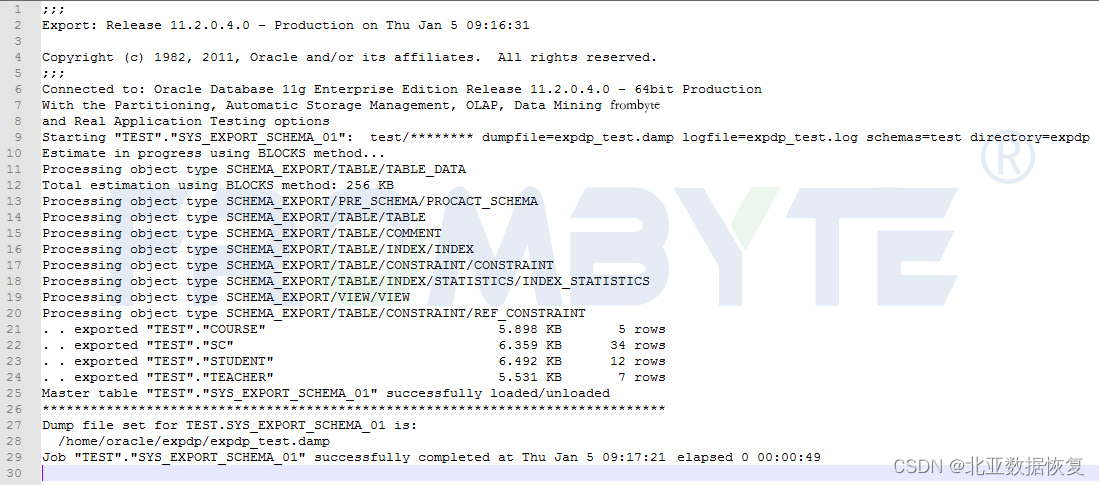
【数据库数据恢复】Oracle数据库ASM磁盘组数据恢复案例
oracle数据库故障&分析: oracle数据库ASM磁盘组掉线,ASM实例不能挂载。数据库管理员尝试修复数据库,但是没有成功。 oracle数据库数据恢复过程: 1、将oracle数据库所涉及磁盘以只读方式备份。后续的数据分析和数据恢复操作都…...
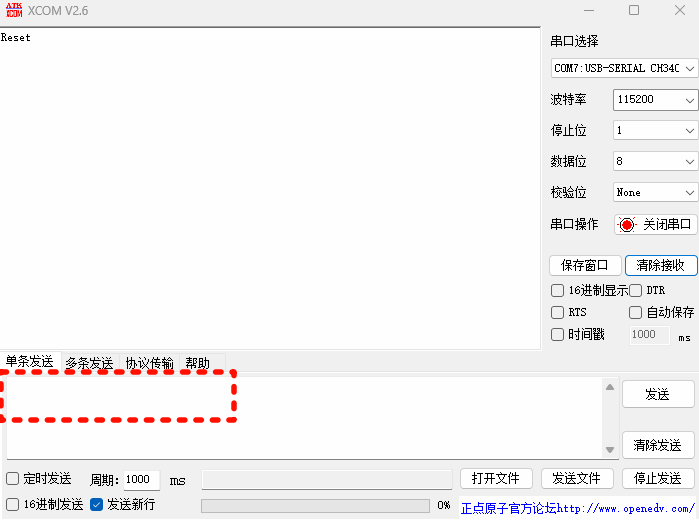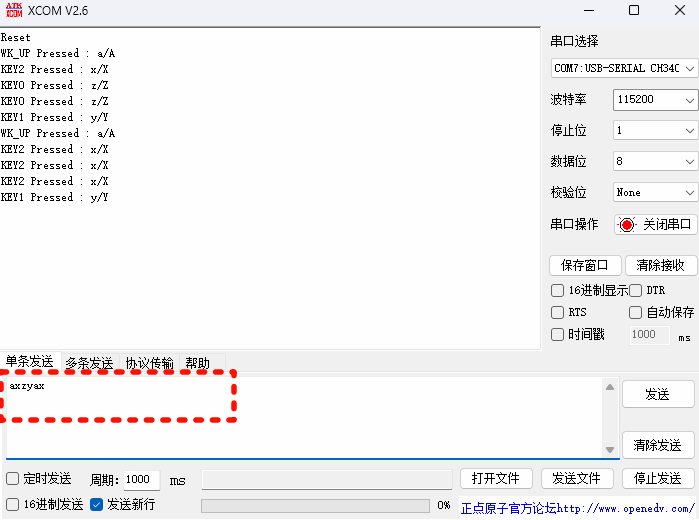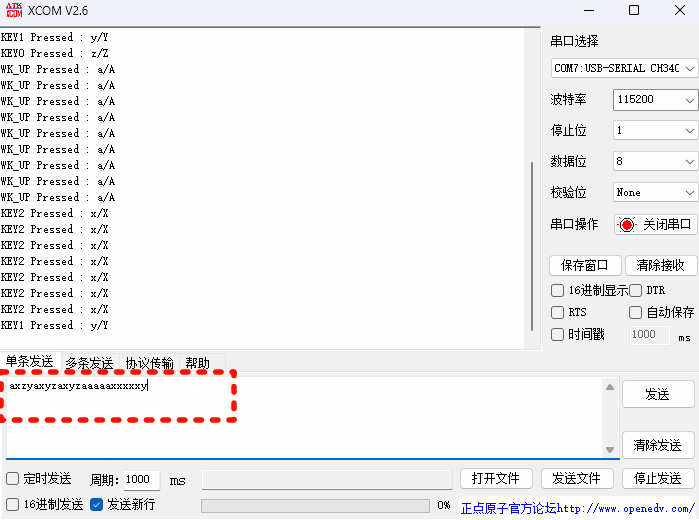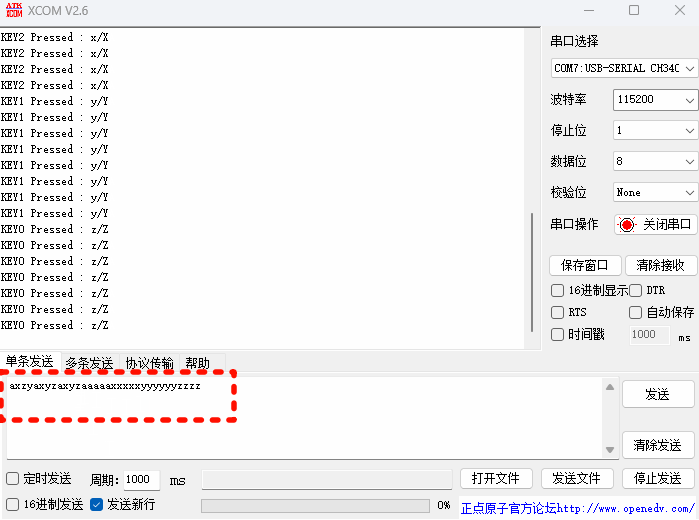
STM32CubeMX教程31 USB_DEVICE - HID外设_模拟键盘或鼠标
目录 1、准备材料 2、实验目标 3、模拟鼠标实验流程 3.0、前提知识 3.1、CubeMX相关配置 3.1.0、工程基本配置 3.1.1、时钟树配置 3.1.2、外设参数配置 3.1.3、外设中断配置 3.2、生成代码 3.2.0、配置Project Manager页面 3.2.1、设初始化调用流程 3.2.2、外设中…...

知道Wi-Fi名称和密码之后自动连接
这里写自定义目录标题 有Wi-Fi名称和密码自动连接Wi-Fi主Activity服务类 WIFIStateReceiver工具类 WIFIConnectionManager 有Wi-Fi名称和密码自动连接Wi-Fi 主Activity public class MainActivity extends AppCompatActivity implements View.OnClickListener{private static…...

本地搭建Plex私人影音网站并结合内网穿透实现公网远程访问
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
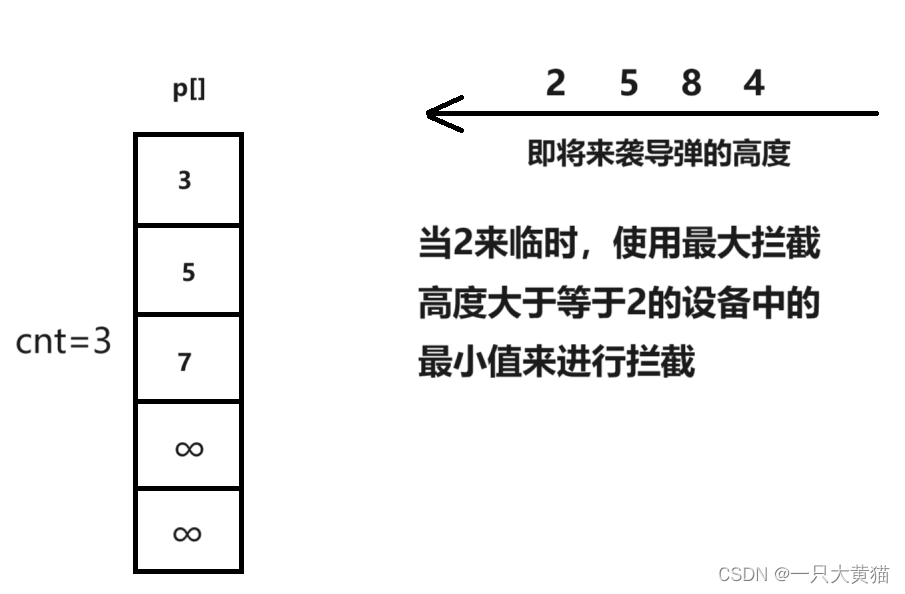
【算法】拦截导弹(线性DP)
题目 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。 但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。 某天,雷达捕捉到敌国的导弹来袭。 由于该系…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
