从交通信号灯看流控和拥塞控制
局部的效率和全局的公平一直都是矛盾的双方。对一个统计复用系统,局部效率由流控决定,而全局公平由拥塞控制决定。
交通信号灯是个典型的分时复用流控的实例,但我经常看到绿灯方向没有任何车辆通过,红灯方向却排成了长龙,这是个不佳的策略。如果是 Linux kernel,早有一堆人卷 patch 了。
可明明只需要实时 “观测” 统计一下流量,设置一下信号灯就行了,这么简单的操作背后还有什么考虑?
作为分时复用系统,目之所及重要的是调度策略,调度器不能忍受资源闲置,十字路口竟然闲置了一半容量,这是失败的策略。
但从拥塞控制角度看,局部转移视线到全局,如果根据实时流量切换信号灯,这种策略可能从 “心理” 上影响司机,而造成流量颠簸。
人的行为具有规律性,某司机每个工作日某时通过某路口时总是绿灯,接下来某个路口是红灯,这是每天开车上下班路上用时几乎相等的原因,周一到周五下班路上时间大概率是 40 分钟,41 分钟,38 分钟,39 分钟,43 分钟,但几乎不可能是 40 分钟,73 分钟,25 分钟,58 分钟,91 分钟,所以不要以堵车作不确定的借口。
按固定间隔调度信号灯,流量是收敛的。但根据实时流量调度,就不好收敛了。如果某司机发现空闲道路有更大概率遇到红灯,那么他可能会换另一条路,影响另一条路的流量,加剧拥塞,当绿灯道路拥堵到让司机宁可等红灯也不想排队时,流量就颠簸了,最终再次影响信号灯。
注意,从流控视角,是拥塞导致了绿灯,但从自私的拥塞控制视角,司机会颠倒因果,为了不等红灯而加入拥塞。
实时调度的流量带有博弈性质,颠簸而不收敛。
互联网流量调度大概也是如此,QoS 要看全局而非当前节点,如果某 queue 空闲,其它流量能被调度到该 queue 吗?假设可以,如果有条流 “发现” 了这个恩惠,它会发送更多数据,从而拥塞加剧,这有损全局公平性。
曾经我觉得公路交通作为一个统计复用系统,通行时间不确定,但后来我发现这个时间波动性很小,唯一可能对时间造成比较大影响的是交通事故。并道,等红灯这些时间几乎固定。每天坐地铁,你同样会发现身边的人也是同样的人,统计复用系统的行为其实非常固定,这固定的背后应该就是每个节点的固定调度策略。
但当我跟别人说这个固定模式时,没人相信我,没有人相信这是固定的。我曾经提到过一种新样式的拥塞控制算法,利用这种固定的模式来决策发送,但仔细想想,发现点有趣的端倪,如果足够多的 sender 都基于观察到的固定流量模式做决策,固定流量模式本身也就消失了,系统重新开始博弈,颠簸。
到底怎么回事?固定的策略导致固定的流量模式,但固定的流量模式却不能被利用,这是一个从阿拉丁神灯里跳出来的俄罗斯套娃。
每个路口的调度策略可以根据时段切换,但根据实时流量切换又不影响全局,难度很大,要避免他们发现这个策略,还要让他们利用这个策略疏导拥塞,这本身就是矛盾。
浙江温州皮鞋湿,下雨进水不会胖。
相关文章:

从交通信号灯看流控和拥塞控制
局部的效率和全局的公平一直都是矛盾的双方。对一个统计复用系统,局部效率由流控决定,而全局公平由拥塞控制决定。 交通信号灯是个典型的分时复用流控的实例,但我经常看到绿灯方向没有任何车辆通过,红灯方向却排成了长龙…...
【LinkedList】| 深度剥析Java SE 源码合集Ⅰ
目录一. 🦁 LinkedList介绍二. 🦁 结构以及对应方法分析2.1 结构组成2.1.1 节点类2.1.2 成员变量2.2 方法实现2.2.1 添加add(E e)方法2.2.2 头尾添加元素Ⅰ addFirst(E e)Ⅱ addLast(E e)2.2.3 查找get(int index)方法2.2.4 删除remove()方法三. &#x…...
黑马程序员7
算数运算符重载 运算符重载概念:对已有的运算符重新进行定义,赋予其另一种功能,以适应不同的数据类型 加号运算符 通过自己写函数,实现两个对象相加属性后返回新的对象 两种方式重载 成员函数方式重载 全局函数重载 上来 perso…...
Qt安装与使用经验分享;无.pro文件;无QTextCodec file;Qt小试;界面居中;无缝;更换Qt图标;更换Qt标题。
1、切换安装下载源 《Qt安装教程》先推荐一篇安装文章:《Qt安装教程》 Qt 5.15 之后已经不提供离线安装包了,就是那个 3.7G 的 exe 安装包。请看官方说明,所以只能用在线安装包。 1,下载在线安装包 QT 在线安装包链接ÿ…...
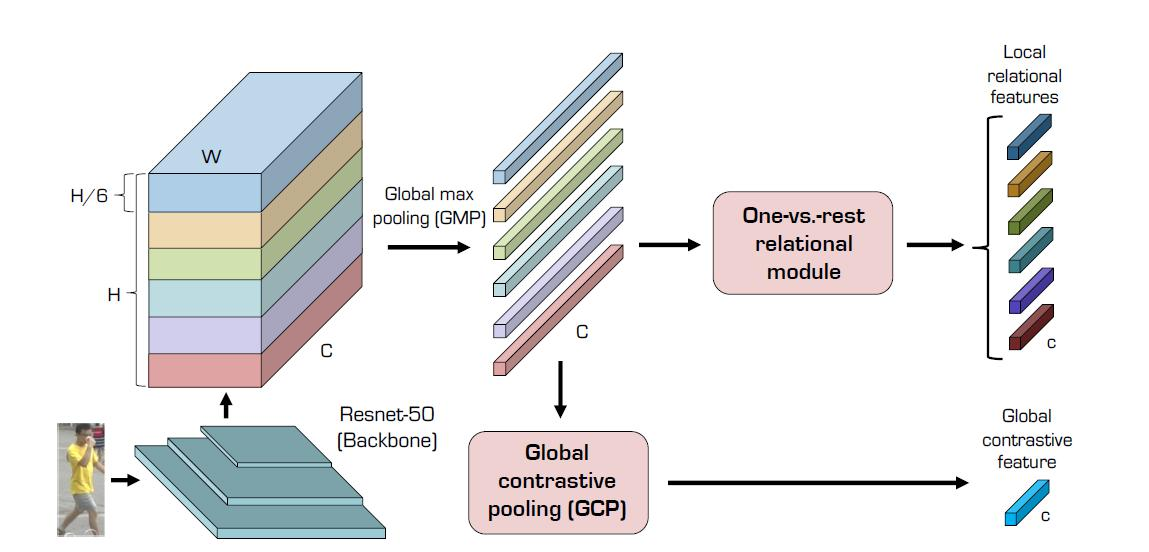
AAAI顶会行人重识别算法详解——Relation Network for Person Re-identification
1.论文整体框架概述 在行人重识别任务中,通常都是对整个输入数据进行特征提取,但是缺少了局部信息。能不能既考虑局部与整体信息,也同时加入他们的联系呢?这篇论文主要的思想就是局部信息和全局信息的融合。 整体流程如上图所示, 首先对整体进行特征提取, 通常采用…...
)
hadoop调优(二)
hadoop调优(二) 1 HDFS故障排除 1.1 NameNode故障处理 NameNode进程挂了并且存储数据丢失了,如何恢复NameNode? 如果NameNode进程挂掉并且数据丢失了,可以利用Secondary NameNode来恢复NameNode。Secondary NameNode主要用于备份NameNode…...

【基础算法】双指针---数组元素的目标和
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...
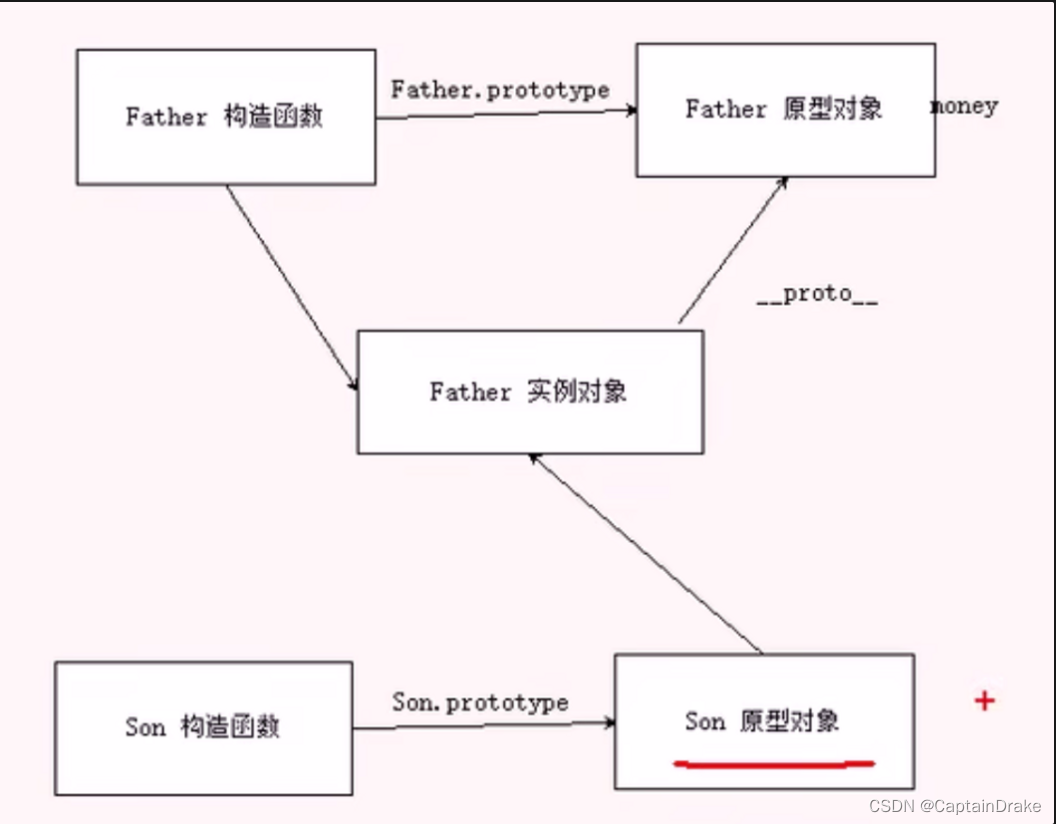
Javascript借用原型对象继承父类型方法
借用原型对象继承父类型方法 目的: 儿子继承父类属性和方法,父类之后新增的方法不会被儿子继承。 前言: 先理解一个问题: Son.prototype Father.prototype; 这一操作相当于把Son的原型对象指向Father。 意味着Son的prototype的地址与Fa…...

你不会工作1年了连枚举都还不知道吧?
💗推荐阅读文章💗 🌸JavaSE系列🌸👉1️⃣《JavaSE系列教程》🌺MySQL系列🌺👉2️⃣《MySQL系列教程》🍀JavaWeb系列🍀👉3️⃣《JavaWeb系列教程》…...
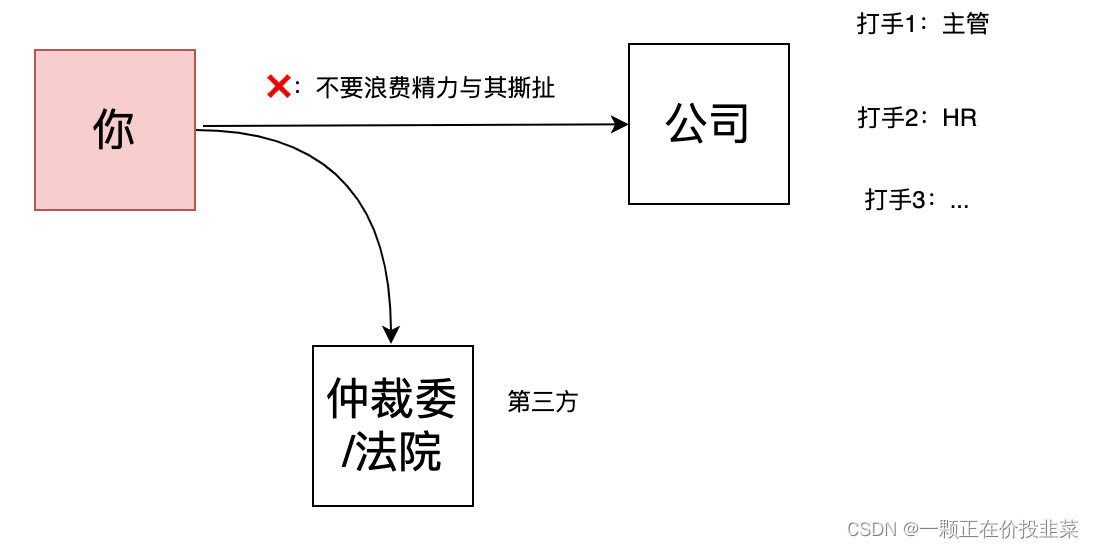
ks通过恶意低绩效来变相裁员(五)绩效申诉就是「小六自证吃了一碗凉粉」
目录 一、小六吃了一碗凉粉 二、给你差绩效 公司告诉你可以绩效申诉 1、公司的实际目的是啥 2、你一旦自证,就掉入了陷阱 三、谁主张谁举证——让公司证明它绩效考核的客观性和公平性 四、针对公司的流氓恶意绩效行为,还有其他招吗 五、当公司用各…...
一阶低通滤波介绍及simulink模型
一阶低通滤波 背景介绍 低通滤波是一种过滤方式,规定低频信号能正常通过,而超过设定临界值的高频信号则被阻隔、减弱。低通滤波可以简单的认为:设定一个频率点,当信号频率高于这个频率时不能通过,在数字信号中&#…...

三十三、MongoDB PHP 扩展
PHP 语言访问 MongoDB 数据库需要使用 mongo 扩展 mongo 扩展不是 PHP 官方内置的扩展,需要开发者自己手动安装和配置 本章我们将学习如何在 Linux、Window、Mac 平台上安装 mongo 扩展 Linux 上安装 PHP MongoDB 扩展 通过 pecl 来安装 在 Linux 系统上可以通…...

2D图像处理:九点标定_上(机械手轴线与法兰轴线重合)(附源码)
文章目录 1. 九点标定2. 九点标定流程2.1 机械手轴线与法兰轴线重合代码实现1. 九点标定 在2D视觉抓取项目中,如果想要让机械手准确的抓取到工件,前提是需要知道机械手应该移动到哪里(位姿)。而移动到哪里(位姿)的获取就需要对相机和机械手进行标定。因此,九点标定(2D视…...
:vector内存预分配,左值引用和右值引用,move语义)
2023最新C++面经(一):vector内存预分配,左值引用和右值引用,move语义
文章目录零、前言一、在C中,往vector插入1000个数字,怎么做能保证性能最高二、在vector中对10000个数字删除偶数位置的数,怎么做保证性能较高三、malloc用delete会出现什么问题四、weak_ptr解决的是什么问题,lock返回的对象可以直接使用吗五、…...

【C语言经典例题】调整数组使奇数全部都位于偶数前面
目录 一、题目要求 二、解题思路 分步解析 从前往后找 从后往前找 交换 三、完整代码演示 一、题目要求 输入一个整数数组,实现一个函数, 来调整该数组中数字的顺序使得数组中所有的奇数位于数组的前半部分, 所有偶数位于数组的后半…...

C++经典20题型,满满知识,看这一篇就够了(含答案)
今天找了20道c的经典题型,看这一篇就够了,全是干货 目录 1、题目:有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总…...

卷积神经网络CNN之ZF Net网络模型详解(理论篇)
1.背景 2. ZF Net模型结构 3. 改进优缺点 一、背景 ZF Net是用作者的名字命名的,Matthew D.Zeiler 和 Rob Fergus (纽约大学),2013年撰写的论文; 论文原网址https://arxiv.org/abs/1311.2901 论文名:Vis…...

Vue 3.0 响应性 基础 【Vue3 从零开始】
#声明响应式状态 要为 JavaScript 对象创建响应式状态,可以使用 reactive 方法: import { reactive } from vue// 响应式状态const state reactive({count: 0}) reactive 相当于 Vue 2.x 中的 Vue.observable() API ,为避免与 RxJS 中的 ob…...
flex布局方式让最后一个(或第二个...n)元素居右显示
<div class"round"> <div class"income">收入</div> <div class"center"> <img style"width: 12px" src"../../img/big/up.png"> </div> <div class"rg"> <span cl…...

【Python语言基础】——Python MySQL Order By
Python语言基础——Python MySQL Order By 文章目录 Python语言基础——Python MySQL Order By一、Python MySQL Order By一、Python MySQL Order By 结果排序 请使用 ORDER BY 语句按升序或降序对结果进行排序。 ORDER BY 关键字默认按升序对结果进行排序。若要按降序对结果进…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
