实验一 Python编程基础
目录
一、实验目标
二、实验内容
1.绘制如下图形 ,一个正方形,内有三个红点,中间红点在正方形中心。
2.使用turtle库绘制如下图形:
3.绘制奥运五环图
4.回文问题
5.身份证性别判别
6.数据压缩
7.验证哥德巴赫猜想
8.使用蒙特 · 卡罗方法计算圆周率近似值问题
9.爬楼梯问题
10.年份判断
11.选做题:汉诺塔问题。
一、实验目标
1.了解Python的基本编程环境,熟悉其主要组成部分和使用。
2.熟悉turtle库语法元素,了解其绘图坐标体系、画笔控制函数和运动命令函数。通过程序实例,初步掌握Python程序设计的基本概念、编程规则和开发过程。
3.掌握Python的基本数据类型的概念和使用;
4.运用Python的标准数学库进行数值计算;
5. 掌握字符串类型的格式化操作方法和应用。
6.熟练运用选择结构与循环结构解决实际问题。
二、实验内容
1.绘制如下图形 ,一个正方形,内有三个红点,中间红点在正方形中心。
| 要求如下:
(1)正方形边长为200,线条为黑色; (2)圆点的直径均为20 ,填充颜色为红色,画完后隐藏画笔; (3)中间圆点的圆心位置为画布正中心,三个圆心之间距离相隔为40。 |
import turtle as tu
tu.setup(width=1.0,height=1.0,startx=0,starty=0)
tu.bgcolor('white')
tu.pencolor('black')
tu.hideturtle()
tu.begin_fill()
tu.fillcolor('red')
tu.circle(10)
tu.end_fill()
tu.penup()
tu.goto(40,0)
tu.pendown()
tu.begin_fill()
tu.fillcolor('red')
tu.circle(10)
tu.end_fill()
tu.penup()
tu.goto(-40,0)
tu.pendown()
tu.begin_fill()
tu.fillcolor('red')
tu.circle(10)
tu.end_fill()
tu.penup()
tu.goto(-100,-100)
tu.pendown()
for i in range(4):tu.forward(200)tu.left(90)
tu.penup()
tu.goto(-20,200)
tu.pendown()
tu.mainloop()2.使用turtle库绘制如下图形:

(1)画一个由一个正方形和一个菱形组成的图形,其中,正方形的边长为200象素,菱形的四个顶点均在正方形四条边的中点上;
(2)设置画笔速度为1;
(3)菱形的填充颜色为红色,所有线条为黑色;
(4)画图结束,隐藏并停止画笔。
import turtle as tu
tu.hideturtle()
tu.setup(1.0,1.0,0,0)
tu.bgcolor('white')
tu.penup()
tu.goto(-100,-100)
tu.pendown()
for i in range(4):tu.forward(200)tu.left(90)
tu.penup()
tu.goto(0,-100)
tu.left(45)AC
tu.pendown()
tu.begin_fill()
tu.fillcolor("red")
for i in range(4):tu.forward(141)tu.left(90)
tu.end_fill()
tu.penup()
tu.goto(-20,200)
tu.pendown()
tu.mainloop()3.绘制奥运五环图
其中五种颜色分别为蓝色、黑色、红色、黄色和绿色。注意根据实际效果调整圆形的大小和位置。

import turtle as tu
tu.setup(1.0,1.0,0,0)
tu.hideturtle()
tu.bgcolor('white')
tu.pencolor('black')
tu.pensize(5)
tu.circle(50)
tu.penup()
tu.goto(-120,0)
tu.pendown()
tu.pencolor('blue')
tu.pensize(5)
tu.circle(50)
tu.penup()
tu.goto(120,0)
tu.pendown()
tu.pencolor('red')
tu.pensize(5)
tu.circle(50)
tu.penup()
tu.goto(60,-60)
tu.pendown()
tu.pencolor('green')
tu.pensize(5)
tu.circle(50)
tu.penup()
tu.goto(-60,-60)
tu.pendown()
tu.pencolor('yellow')
tu.pensize(5)
tu.circle(50)
tu.penup()
tu.goto(-20,200)
tu.pendown()
tu.pencolor('black')
tu.mainloop()4.回文问题
输入一个字符串,判断一个字符串是不是回文。
def f(s):for i in range(len(s)):if s[i]!=s[len(s)-i-1]:return Falsereturn True
print(f(input()))5.身份证性别判别
输入一个18位字符组成的身份证号,其中第17位表示性别,如果是奇数表示男性,是偶数表示女性,编写代码实现判断输入的一个身份证号是男性还是女性。
def f(s):if int(s[16])%2==0:print('woman')else:print('man')
f(input())6.数据压缩
用两个数据表示一段连续相同的字符,第一个数据记录指定字符重复相同的次数,第二个记录具体字符值。例如输入字符串“AAAABBBCC”,输出“4A3B2C”
def f(s):res=[]dic={}for i in s:if i in res:dic[i]+=1else:res.append(i)dic[i]=1for i in res:print("%d%s"%(dic[i],i),end='')
f("AAAABBBCC")7.验证哥德巴赫猜想
任何大于2的偶数,都可以表示为两个素数之和。输入一个大于2的偶数,若猜想成功屏幕上输出哥德巴赫猜想等式,否则输出“Failed”。
例如:输入100,输出97+3。
def su(n):for i in range(2,n//2+1):if n%i==0:return Falsereturn True
def f(n):for i in range(2,n//2+1):if su(i) and su(n-i):print(("%d+%d")%(n-i,i))returnprint('Failed')return
f(100)8.使用蒙特 · 卡罗方法计算圆周率近似值问题
试着编写程序,模拟蒙特·卡罗计算圆周率近似值的方法,输入掷飞镖次数,然后输出圆周率近似值。
蒙特·卡罗方法是一种通过概率来得到问题近似解的方法,在很多领域都有重要的应用,其中就包括圆周率近似值的计算问题。假设有一块边长为 2 的正方形木板,上面画一个单位圆,然后随意往木板上扔飞镖,落点坐标(x, y)必然在木板上(更多的时候是落在单位圆内),如果扔的次数足够多,那么落在单位圆内的次数除以总次数再乘以 4,这个数字会无限逼近圆周率的值。
提示:random模块用法
import random #导入random模块
random.random()产生0-1之间的一个随机数
import random as r
n=1000000
sums=0
for i in range(n):x=r.uniform(0,1)y=r.uniform(0,1)if (x-0.5)*(x-0.5)+(y-0.5)*(y-0.5)<=0.25:sums+=1
print(sums/n*4)9.爬楼梯问题
假设一段楼梯共 15 个台阶,小明一步最多能上 3 个台阶。输入小明上的台阶,计算小明上这段楼梯一共有多少种方法。从第15个台阶上往回看,有3种方法可以上来(从第14个台阶上一步迈1个台阶上来,从第13个台阶上一步迈2个台阶上来,从第12个台阶上一步迈3个台阶上来),同理,第14个、13个、12个台阶都可以这样推算,从而得到公式f(n) = f(n-1) + f(n-2) + f(n-3),其中n=15、14、13、...、5、4。然后确定这个递归公式的结束条件了,第一个台阶只有1种上法,第二个台阶有2种上法(一步迈2个台阶上去、一步迈1个台阶分两步上去),第三个台阶有4种上法,….
def f(n):if n<0:return 0if n==0:return 1return weimeng(n-1)+weimeng(n-2)+weimeng(n-3)
print(f(15))10.年份判断
输入某一个年份,输出该年份开始的12个年份及对应的天干地支与生肖。例如:
输入:2009年
输出:
2009 己丑 牛
...【中间部分省略了,程序测试效果要输出】
2020 庚子 鼠
year = int(input("请输入年份:"))
tiangan = ['甲', '乙', '丙', '丁', '戊', '己', '庚', '辛', '壬', '癸']
dizhi = ['子', '丑', '寅', '卯', '辰', '巳', '午', '未', '申', '酉', '戌', '亥']
shengxiao = ['鼠', '牛', '虎', '兔', '龙', '蛇', '马', '羊', '猴', '鸡', '狗', '猪']
gan = tiangan[(year - 4)%10]
zhi = dizhi[(year - 4)%12]
xiao = shengxiao[(year - 4)%12]
for i in range(year, year + 12):gan = tiangan[(i - 4)%10]zhi = dizhi[(i - 4)%12]xiao = shengxiao[(i - 4)%12]print(i, gan, zhi, xiao)11.选做题:汉诺塔问题。
据说古代有一个梵塔,塔内有三个底座 A、B、C,A 座上有 64 个盘子,盘子大小不等,大的在下,小的在上。有一个和尚想把这 64 个盘子从 A 座移到 C 座,但每次只能允许移动一个盘子。在移动盘子的过程中可以利用 B 座,但任何时刻 3 个座上的盘子都必须始终保持大盘在下、小盘在上的顺序。如果只有一个盘子,则不需要利用 B 座,直接将盘子从 A 移动到 C 即可。编写函数,接收一个表示盘子数量的参数和分别表示源、目标、临时底座的参数,然后输出详细移动步骤和每次移动后三个底座上的盘子分布情况。
t=1
def f(n,a,b,c):global tif n==1:print("%d.Move %d from %s to %s"%(t,n,a,c))t+=1return Nonef(n-1,a,c,b)print("%d.Move %d from %s to %s"%(t,n,a,c))t+=1f(n-1,b,a,c)
n=int(input())
a,b,c='a','b','c'
f(n,a,b,c)相关文章:

实验一 Python编程基础
目录 一、实验目标 二、实验内容 1.绘制如下图形 ,一个正方形,内有三个红点,中间红点在正方形中心。 2.使用turtle库绘制如下图形: 3.绘制奥运五环图 4.回文问题 5.身份证性别判别 6.数据压缩 7.验证哥德巴赫猜想 8.使…...
ThreadLocal介绍和理解)
java多线程(十五)ThreadLocal介绍和理解
一、对ThreadLocal的理解 ThreadLocal,很多地方叫做线程本地变量,也有些地方叫做线程本地存储,其实意思差不多。可能很多朋友都知道ThreadLocal为变量在每个线程中都创建了一个副本,那么每个线程可以访问自己内部的副本变量。这句…...
K8S 实用工具之三 - 图形化 UI Lens
开篇 📜 引言: 磨刀不误砍柴工工欲善其事必先利其器 第一篇:《K8S 实用工具之一 - 如何合并多个 kubeconfig?》第二篇:《K8S 实用工具之二 - 终端 UI K9S》 像我这种,kubectl 用的不是非常溜,经…...
HDMI协议介绍(六)--EDID
目录 什么是EDID EDID结构 1)Header Information 头信息(厂商信息、EDID 版本等) (2)Basic Display Parameters and Features 基本显示参数(数字/模拟接口、屏幕尺寸、格式支持等) (3)色度信息 (4)Established Timings(VESA 定义的电脑使用 Timings) (5)Standard Timing…...
【项目实战】Linux下安装Nginx教程
一、环境准备 Linux版本:CentOS7 64位 二、具体步骤 2.1 步骤1:确认系统中安装以下基础依赖 确认系统中安装了gcc、pcre-devel、zlib-devel、openssl-devel。 在安装Nginx前首先要确认系统中安装了gcc、pcre-devel、zlib-devel、openssl-devel。 yu…...

【数据结构】链式二叉树
前言 在前面我们学习了一些二叉树的基本知识,了解了它的结构以及一些性质,我们还用数组来模拟二叉树建立了堆,并学习了堆排序,可是数组结构的二叉树有很大的局限性,平常我们用的最多树结构的还是链式二叉树,…...
CentOS安装RStudio-Server的方法
R语言是生信分析、数据挖掘最常用最好用的软件之一,得到了广大生信工程师、数据分析师的厚爱。Rstudio 是 R 的集成开发环境,使得R语言的用户体验更强。一般个人电脑(PC, Personal Computer)使用单机版的 Rstudio 即可,…...

从交通信号灯看流控和拥塞控制
局部的效率和全局的公平一直都是矛盾的双方。对一个统计复用系统,局部效率由流控决定,而全局公平由拥塞控制决定。 交通信号灯是个典型的分时复用流控的实例,但我经常看到绿灯方向没有任何车辆通过,红灯方向却排成了长龙…...
【LinkedList】| 深度剥析Java SE 源码合集Ⅰ
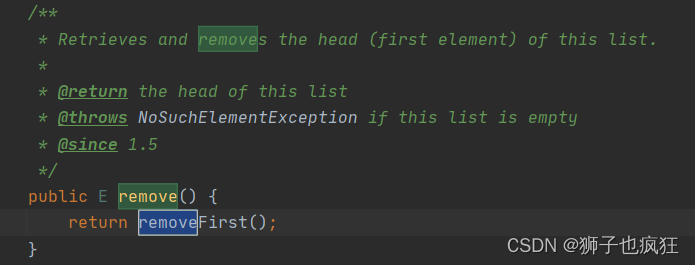
目录一. 🦁 LinkedList介绍二. 🦁 结构以及对应方法分析2.1 结构组成2.1.1 节点类2.1.2 成员变量2.2 方法实现2.2.1 添加add(E e)方法2.2.2 头尾添加元素Ⅰ addFirst(E e)Ⅱ addLast(E e)2.2.3 查找get(int index)方法2.2.4 删除remove()方法三. &#x…...
黑马程序员7
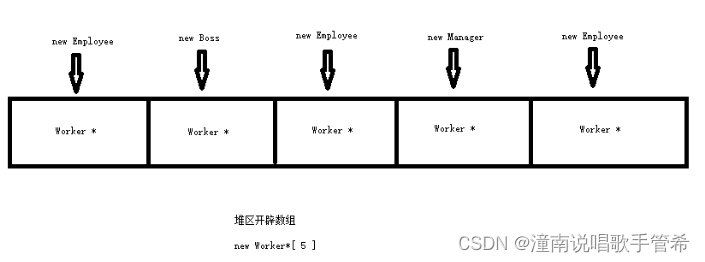
算数运算符重载 运算符重载概念:对已有的运算符重新进行定义,赋予其另一种功能,以适应不同的数据类型 加号运算符 通过自己写函数,实现两个对象相加属性后返回新的对象 两种方式重载 成员函数方式重载 全局函数重载 上来 perso…...
Qt安装与使用经验分享;无.pro文件;无QTextCodec file;Qt小试;界面居中;无缝;更换Qt图标;更换Qt标题。
1、切换安装下载源 《Qt安装教程》先推荐一篇安装文章:《Qt安装教程》 Qt 5.15 之后已经不提供离线安装包了,就是那个 3.7G 的 exe 安装包。请看官方说明,所以只能用在线安装包。 1,下载在线安装包 QT 在线安装包链接ÿ…...
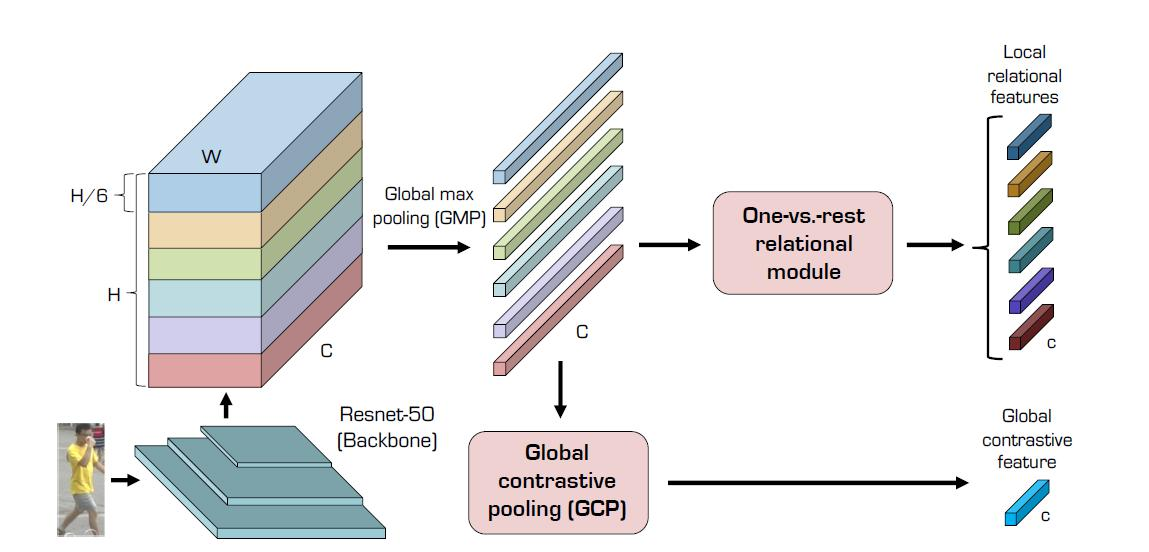
AAAI顶会行人重识别算法详解——Relation Network for Person Re-identification
1.论文整体框架概述 在行人重识别任务中,通常都是对整个输入数据进行特征提取,但是缺少了局部信息。能不能既考虑局部与整体信息,也同时加入他们的联系呢?这篇论文主要的思想就是局部信息和全局信息的融合。 整体流程如上图所示, 首先对整体进行特征提取, 通常采用…...
)
hadoop调优(二)
hadoop调优(二) 1 HDFS故障排除 1.1 NameNode故障处理 NameNode进程挂了并且存储数据丢失了,如何恢复NameNode? 如果NameNode进程挂掉并且数据丢失了,可以利用Secondary NameNode来恢复NameNode。Secondary NameNode主要用于备份NameNode…...

【基础算法】双指针---数组元素的目标和
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...
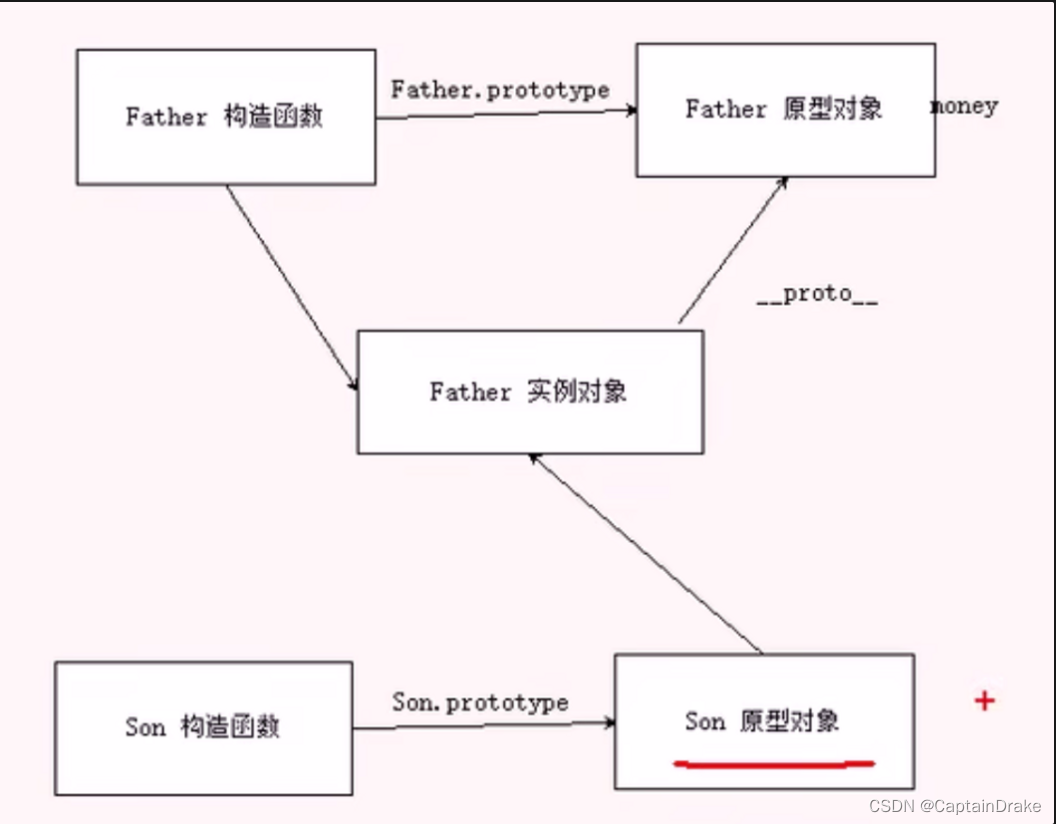
Javascript借用原型对象继承父类型方法
借用原型对象继承父类型方法 目的: 儿子继承父类属性和方法,父类之后新增的方法不会被儿子继承。 前言: 先理解一个问题: Son.prototype Father.prototype; 这一操作相当于把Son的原型对象指向Father。 意味着Son的prototype的地址与Fa…...

你不会工作1年了连枚举都还不知道吧?
💗推荐阅读文章💗 🌸JavaSE系列🌸👉1️⃣《JavaSE系列教程》🌺MySQL系列🌺👉2️⃣《MySQL系列教程》🍀JavaWeb系列🍀👉3️⃣《JavaWeb系列教程》…...
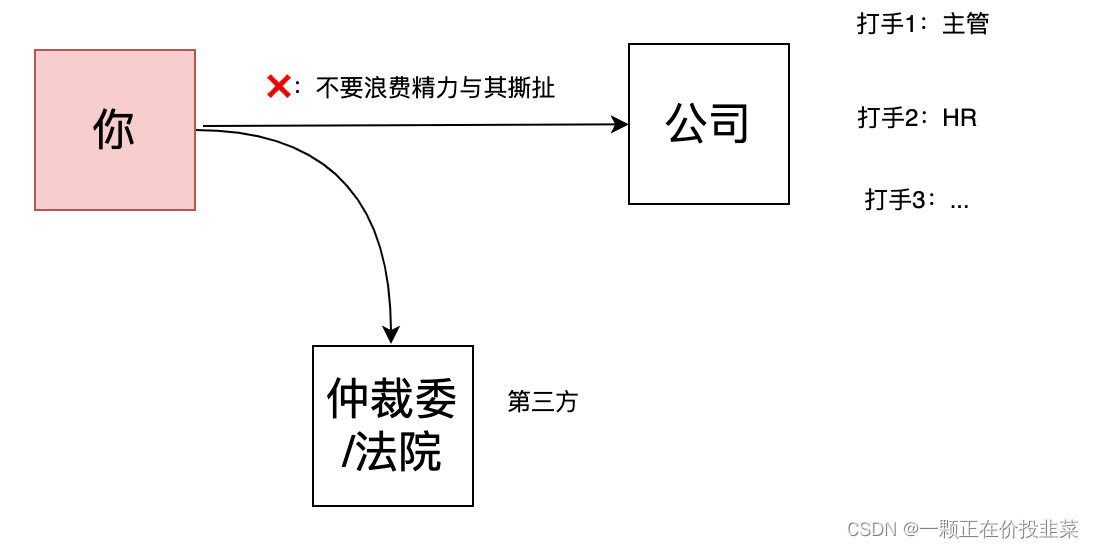
ks通过恶意低绩效来变相裁员(五)绩效申诉就是「小六自证吃了一碗凉粉」
目录 一、小六吃了一碗凉粉 二、给你差绩效 公司告诉你可以绩效申诉 1、公司的实际目的是啥 2、你一旦自证,就掉入了陷阱 三、谁主张谁举证——让公司证明它绩效考核的客观性和公平性 四、针对公司的流氓恶意绩效行为,还有其他招吗 五、当公司用各…...
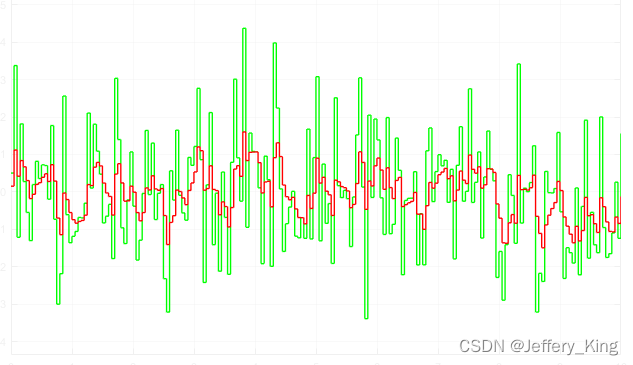
一阶低通滤波介绍及simulink模型
一阶低通滤波 背景介绍 低通滤波是一种过滤方式,规定低频信号能正常通过,而超过设定临界值的高频信号则被阻隔、减弱。低通滤波可以简单的认为:设定一个频率点,当信号频率高于这个频率时不能通过,在数字信号中&#…...

三十三、MongoDB PHP 扩展
PHP 语言访问 MongoDB 数据库需要使用 mongo 扩展 mongo 扩展不是 PHP 官方内置的扩展,需要开发者自己手动安装和配置 本章我们将学习如何在 Linux、Window、Mac 平台上安装 mongo 扩展 Linux 上安装 PHP MongoDB 扩展 通过 pecl 来安装 在 Linux 系统上可以通…...

2D图像处理:九点标定_上(机械手轴线与法兰轴线重合)(附源码)
文章目录 1. 九点标定2. 九点标定流程2.1 机械手轴线与法兰轴线重合代码实现1. 九点标定 在2D视觉抓取项目中,如果想要让机械手准确的抓取到工件,前提是需要知道机械手应该移动到哪里(位姿)。而移动到哪里(位姿)的获取就需要对相机和机械手进行标定。因此,九点标定(2D视…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...

自定义线程池1.2
自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本,将线程池中的线程数量交给使用者决定,并且将线程的创建延迟到任务提交的时候,在本文中我们将对这个版本进行如下的优化: 在新建线程时交给线程一个任务。让线程在某种情况下…...

HTML版英语学习系统
HTML版英语学习系统 这是一个完全免费、无需安装、功能完整的英语学习工具,使用HTML CSS JavaScript实现。 功能 文本朗读练习 - 输入英文文章,系统朗读帮助练习听力和发音,适合跟读练习,模仿学习;实时词典查询 - 双…...

