蓝桥杯算法赛第4场小白入门赛强者挑战赛
蓝桥杯算法赛第4场小白入门赛&强者挑战赛
- 小白1
- 小白2
- 小白3
- 强者1
- 小白4强者2
- 小白5强者3
- 小白6强者4
- 强者5
- 强者6
链接:
第 4 场 小白入门赛
第 4 场 强者挑战赛
小白1
直接用C++内置函数即可。
#include <bits/stdc++.h>
using namespace std;#include <bits/extc++.h>
using namespace __gnu_pbds;using llt = long long;
using Real = double;
using vi = vector<int>;int main(){
#ifndef ONLINE_JUDGEfreopen("z.txt", "r", stdin);
#endifios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(0);cout << __builtin_popcount(2024) << endl;return 0;
}
小白2
做个字典即可。
import os
import sys
p = {'yuanxing':1, 'zhengfangxing':2, 'changfangxing':3, 'sanjiaoxing':4, 'tuoyuanxing':5, 'liubianxing':6}n = int(input())
a = input().split()
ans = 0
for i in a:ans += p[i]
print(ans)
小白3
经典的NIM问题。当异或和为零时,先手必败。所以当石子数量为偶数时,分成两堆即可。当数量为奇数时,无论怎么分,最低位的1不可能异或为零,也就是说异或和必不为零,先手必胜。
#include <iostream>
using namespace std;
int main()
{int n; cin >> n;cout << (n % 2 == 0 ? "B" : "A") << "\n"; return 0;
}
强者1
很明显的贪心,无论轮到谁取,均取当前最大的数即可。
#include <bits/stdc++.h>
using namespace std;#include <bits/extc++.h>
using namespace __gnu_pbds;using llt = long long;
using Real = double;
using vi = vector<int>;
using pii = pair<int, int>;int N;
vi A;void proc(){ sort(A.begin(), A.end(), greater<int>());llt a[2] = {0};int o = 0;for(int i=1;i<N;i+=2){a[o] += A[i - 1];a[o ^ 1] += A[i];o ^= 1;}cout << a[0] << " " << a[1] << endl;
}int main(){
#ifndef ONLINE_JUDGEfreopen("z.txt", "r", stdin);
#endifios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(0);cin >> N;A.assign(N, {});for(auto & i : A) cin >> i;proc();return 0;
}
小白4强者2
抽屉原理。因为总取值范围为36500,所以当取数数量超过100时,必然有两个数之差在365及其以内。当数量不超过100时,排序以后逐个检验一下即可。
#include <bits/stdc++.h>
using namespace std;#include <bits/extc++.h>
using namespace __gnu_pbds;using llt = long long;
using Real = double;
using vi = vector<int>;int N;
int Q;
vi A;const array<string, 2> ANS = {"NO", "YES"};int proc(int s, int e){if(e >= s + 100) return 1;vi vec(A.begin() + s, A.begin() + e + 1);sort(vec.begin(), vec.end());for(int i=1,n=vec.size();i<n;++i){if(vec[i] - vec[i - 1] <= 365) return 1;}return 0;
}int main(){
#ifndef ONLINE_JUDGEfreopen("z.txt", "r", stdin);
#endifios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(0);cin >> N >> Q;A.assign(N, {});for(auto & i : A) cin >> i;for(int s,e,q=1;q<=Q;++q){cin >> s >> e;cout << ANS[proc(s - 1, e - 1)] << "\n"; }return 0;
}
小白5强者3
逆序对树状数组相关。首先把二元组的数组计算出来,每个元素是 ( i , P A i ) (i, P_{A_i}) (i,PAi)。这个很容易计算。将二元组数组看做是 ( x , y ) (x,y) (x,y)的数组,所以该题的条件其实就是一个二维偏序的条件,即两个维度都要小。然后该题本质上就是对每一个点 ( x i , y i ) (x_i,y_i) (xi,yi)求:
c i × x + i − ∑ j 是 i 左下的点 x j c_i\times{x+i} - \sum_{j是i左下的点}{x_j} ci×x+i−j是i左下的点∑xj
其中 c i c_i ci是位于 i i i点左下的所有点的数量。
弄两个树状数组,记作b1和b2,则对每一个点 ( x , y ) (x,y) (x,y):
- 在b1中查询[1, y)的和,该和表示一共有多少个点位于左下,记作c
- 在b2中查询[1, y)的和,该和表示左下点x坐标之和, 记作s
- 然后将 c * x - s 累加进去即可
- 然后将 b1[y] 加 1, b2[y] 加 x 即可
#include <bits/stdc++.h>
using namespace std;#include <bits/extc++.h>
using namespace __gnu_pbds;using llt = long long;
using Real = double;
using vi = vector<int>;struct FenwickTree{ // 树状数组using value_type = long long int;
using vec_type = vector<value_type>;int n;
vec_type c;FenwickTree() = default;static int lowbit(int x){return x & -x;}void init(int nn){this->c.assign((this->n=nn) + 1, 0);}void modify(int pos, value_type delta){for(int i=pos;i<=this->n;i+=lowbit(i)) this->c[i] += delta;
}value_type query(int pos)const{value_type ans = 0;for(int i=pos;i;i-=lowbit(i)) ans += this->c[i];return ans;
}value_type query(int s, int e)const{return this->query(e) - this->query(s - 1);}}Bt1, Bt2;using pii = pair<int, int>;int N;
vi A, B;void input(vi & v, int n){v.assign(n, {});for(auto & i : v) cin >> i;
}llt proc(){vi pos(N + 1, {});for(int i=0;i<N;++i) pos[B[i]] = i;vector<pair<int, int>> vec(N);for(int i=0;i<N;++i){vec[i] = {i + 1, pos[A[i]] + 1};}// sort(vec.begin(), vec.end(), [](pii a, pii b){return a.second < b.second;});llt ans = 0;Bt1.init(N); Bt2.init(N);for(int i=0;i<N;++i){auto k = vec[i].first;auto v = vec[i].second;auto c = Bt1.query(v);Bt1.modify(v, 1);auto s = Bt2.query(v);Bt2.modify(v, k);ans += c * k - s;}return ans;
}int main(){
#ifndef ONLINE_JUDGEfreopen("z.txt", "r", stdin);
#endifios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(0);cin >> N;input(A, N); input(B, N);cout << proc() << endl;return 0;
}
小白6强者4
概率推公式。有 N N N个格子,第 i i i格有 P i P_i Pi的概率到下一格(第 N N N格的下一格是第1格),有 1 − P i 1-P_i 1−Pi的概率就此停止。问每一格最终停下的概率,以及对这些概率排序。
对于第1格而言,有 1 − P 1 1-P_1 1−P1的概率直接停下,或者转一圈回来以后再以 1 − P 1 1-P_1 1−P1的概率,或者转二圈再以 1 − P 1 1-P_1 1−P1的概率,……;
对于第2格而言,首先要到达第2格,这个概率是 P 1 P_1 P1,然后剩下的推导类似;
所以,首先令
Π = ∏ i = 1 N P i \Pi=\prod_{i=1}^{N}{P_i} Π=i=1∏NPi
即转一圈的概率。
对第 i i i格,停止在此的概率是:
Q i = P 1 × P 2 × ⋯ × P i − 1 × ( 1 − P i ) × ( 1 + Π + Π 2 + Π 3 + ⋯ ) = P 1 × P 2 × ⋯ × P i − 1 × ( 1 − P i ) × 1 1 − Π Q_i=P_1\times{P_2}\times\cdots\times{P_{i-1}}\times{(1-P_i)}\times\big(1+\Pi+\Pi^2+\Pi^3+\cdots\big)=P_1\times{P_2}\times\cdots\times{P_{i-1}}\times{(1-P_i)}\times\frac{1}{1-\Pi} Qi=P1×P2×⋯×Pi−1×(1−Pi)×(1+Π+Π2+Π3+⋯)=P1×P2×⋯×Pi−1×(1−Pi)×1−Π1
如果不考虑求逆的时间,在 O ( N ) O(N) O(N)内即可求出上述每一个 Q i Q_i Qi。
然后考虑排序,这个比较麻烦,因为要比较概率本身,而不能比较取模以后的数。
考虑 Q i Q_i Qi和 Q j Q_j Qj比较大小,不失一般性,假设 i < j i\lt{j} i<j。则
Q j = P 1 × P 2 × ⋯ × P i − 1 × ( 1 − P i ) × 1 1 − Π Q_j=P_1\times{P_2}\times\cdots\times{P_{i-1}}\times{(1-P_i)}\times\frac{1}{1-\Pi} Qj=P1×P2×⋯×Pi−1×(1−Pi)×1−Π1
Q j = P 1 × P 2 × ⋯ × P i − 1 × P i × ⋯ × ( 1 − P j ) × 1 1 − Π Q_j=P_1\times{P_2}\times\cdots\times{P_{i-1}}\times{P_i}\times\cdots\times{(1-P_j)}\times\frac{1}{1-\Pi} Qj=P1×P2×⋯×Pi−1×Pi×⋯×(1−Pj)×1−Π1
首先讨论特殊情况:
- 当 P i , P j P_i,P_j Pi,Pj全为1时,即不可能停在此2格,停下的概率为零,根据题意, i i i应该排在前面;
- 当 P i , P j P_i,P_j Pi,Pj任意为1时,可知一个停下的概率为零,另一个不为零,则大小关系可以确定。
然后讨论一般情况,即二者全不为1时。可以证明 Q i ≥ Q j Q_i\ge{Q_j} Qi≥Qj。
Q i ≥ Q j ⇔ P 1 × P 2 × ⋯ × P i − 1 × ( 1 − P i ) × 1 1 − Π ≥ P 1 × P 2 × ⋯ × P i − 1 × P i × ⋯ × ( 1 − P j ) × 1 1 − Π ⇔ 1 − P i ≥ P i × ⋯ × ( 1 − P j ) \begin{aligned} Q_i\ge{Q_j} &\Leftrightarrow{P_1\times{P_2}\times\cdots\times{P_{i-1}}\times{(1-P_i)}\times\frac{1}{1-\Pi}}\ge{P_1\times{P_2}\times\cdots\times{P_{i-1}}\times{P_i}\times\cdots\times{(1-P_j)}\times\frac{1}{1-\Pi}}\\ &\Leftrightarrow{1-P_i}\ge{{P_i}\times\cdots\times{(1-P_j)}} \end{aligned} Qi≥Qj⇔P1×P2×⋯×Pi−1×(1−Pi)×1−Π1≥P1×P2×⋯×Pi−1×Pi×⋯×(1−Pj)×1−Π1⇔1−Pi≥Pi×⋯×(1−Pj)
对最后一个不等式的右边做缩放,只需证明
1 − P i ≥ P i × ( 1 − P j ) (*) {1-P_i}\ge{{P_i}\times{(1-P_j)}}\tag{*} 1−Pi≥Pi×(1−Pj)(*)
即可
而 ( ∗ ) (*) (∗)等价于
1 − 2 P i + P i P j ≥ 0 1-2P_i+P_{i}P_j\ge{0} 1−2Pi+PiPj≥0
注意到题目给出的概率的形式,当 P i P_i Pi不为1时,必有 P i ≤ 1 2 P_i\le{\frac{1}{2}} Pi≤21成立。因此最后一个不等式是成立的,从而可知 i i i要排在 j j j前面。
于是得到了一个不必计算概率的具体值就能排序的准则, s o r t sort sort一下即可。
#include <bits/stdc++.h>
using namespace std;#include <bits/extc++.h>
using namespace __gnu_pbds;using llt = long long;
using Real = double;
using vi = vector<int>;llt const MOD = 998244353;llt qpow(llt a, llt n){llt r = 1;while(n){if(n & 1) r = r * a % MOD;a = a * a % MOD;n >>= 1;}return r;
}llt inv(llt a){return qpow(a, MOD-2LL);}int N;
vector<llt> P;llt myhash(const vector<llt> & vec){llt ans = 0;llt k = 0;for(auto i : vec){ans = (ans + (++k) * i % MOD) % MOD;}return ans;
}void proc(){auto tmp = accumulate(P.begin(), P.end(), 0LL);auto pi = inv(qpow(2LL, tmp));auto fenmu = inv((MOD + 1 - pi) % MOD);vector<llt> ans(N);llt fenzi = 1;for(int i=0;i<N;++i){auto p = inv(qpow(2, P[i]));auto q = (MOD + 1 - p) % MOD;ans[i] = fenzi * q % MOD * fenmu % MOD;fenzi = fenzi * p % MOD;}vector<llt> rank(N);for(int i=0;i<N;++i) rank[i] = i + 1;sort(rank.begin(), rank.end(), [&](int i, int j){i -= 1, j -= 1;if(0 == P[i]){ // 100%会走,即停到此处的概率为0if(0 == P[j]) return i < j; return false; // 停在j的概率肯定比i大}if(0 == P[j]) return true;return i < j;});cout << myhash(ans) << endl;cout << myhash(rank) << endl;return;
}int main(){
#ifndef ONLINE_JUDGEfreopen("z.txt", "r", stdin);
#endifios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(0);cin >> N;P.assign(N, {});for(auto & i : P) cin >> i;proc();return 0;
}
强者5
预处理加 D P DP DP。
注意到题目强调了每个用户是独立的,因此首先做一个预处理,计算出二维数组 U s e r 2 G a i n User2Gain User2Gain。 U s e r 2 G a i n [ i ] [ j ] User2Gain[i][j] User2Gain[i][j]表示如果给第 i i i个用户分配 j j j个空间,其收益是多少。收益等于M - 缺页中断数。(为什么要减一下计算收益,因为笔者最开始弄错了,以为是一个分组背包,所以减一下刚好可以计算最大收益)
U s e r 2 G a i n User2Gain User2Gain辅助以数据结构应该比较容易算出来。假设用户的请求数量平均分配为 M / K M/K M/K个,则预处理时间应该是 O ( K × M k log M K ) O(K\times\frac{M}{k}\log{\frac{M}{K}}) O(K×kMlogKM),最差情况可能是 O ( M log M ) O(M\log{M}) O(MlogM)。不太确定这个复杂度对不对。
接下来 D P DP DP,令 D i , j D_{i,j} Di,j表示前 i i i个用户分配 j j j个空间所能获得的最大收益,则
D i , j = max ( D i − 1 , k + U s e r 2 G a i n [ i ] [ j − k ] , k ∈ [ 0 , j ] ) D_{i,j}=\max(D_{i-1,k}+User2Gain[i][j-k],k\in{[0,j]}) Di,j=max(Di−1,k+User2Gain[i][j−k],k∈[0,j])
算出最大收益,再减回来就得到了最小的缺页数。
上述计算要三重循环,看起来是立方的,但实际上不是。考虑到每个用户平均分配到 M K \frac{M}{K} KM个空间,因此,第1个用户只需计算到 M K \frac{M}{K} KM,第2个用户只需计算到 2 M K \frac{2M}{K} K2M,第3个用户到 3 M K \frac{3M}{K} K3M,……
实际计算次数是
( M K + 2 M K + 3 M K + ⋯ + K M K ) × M K ≡ O ( M 2 ) \big(\frac{M}{K}+\frac{2M}{K}+\frac{3M}{K}+\cdots+\frac{KM}{K}\big)\times{\frac{M}{K}}\equiv{O(M^2)} (KM+K2M+K3M+⋯+KKM)×KM≡O(M2)
这似乎也是最差情况。同样不保证这个复杂度分析一定对,感觉没错。
#include <bits/stdc++.h>
using namespace std;#include <bits/extc++.h>
using namespace __gnu_pbds;using llt = long long;
using Real = double;
using vi = vector<int>;
using pii = pair<int, int>;__gnu_pbds::priority_queue<pii, function<bool(const pii &, const pii &)>> Q([](const pii & a, const pii & b){assert(a.second != b.second);return a.second < b.second;
});int N, K, M;
vector<pii> Req;
vi Lisan;
vector<vi> User2Gain;
vector<vi> D;int proc(const vi & req, int alloc){map<int, pair<vi, int>> req2pos;for(int i=0;i<req.size();++i) req2pos[req[i]].first.emplace_back(i);Q.clear();int k = 1;for(auto & p : req2pos){p.second.second = 0;p.second.first.emplace_back(M + M + k++);}vi flag(M + 1, 0);int ans = 0;int used = 0;for(int i=0;i<req.size();++i){auto r = req[i];if(0 == flag[r]){ans += 1;if(used < alloc){used += 1;}else{while(1){auto h = Q.top();Q.pop();if(h.second > i){flag[h.first] = 0;break;}}}}flag[r] = 1;auto & mm = req2pos[r];Q.push({r, mm.first[++mm.second]});}return ans;
}void proc(const vi & req, vi & gain){vi flag(M + 1, 0);int n = 0;for(auto i : req){if(flag[i] == 0){flag[i] = 1;n += 1;}}if(n > N) n = N;gain.assign(n + 1, 0);gain[0] = M - req.size();for(int i=1;i<=n;++i){gain[i] = M - proc(req, i);}return;
}int proc(){Lisan.clear(); Lisan.reserve(M + 1);Lisan.emplace_back(0);for(const auto & p : Req) Lisan.emplace_back(p.second);sort(Lisan.begin(), Lisan.end());Lisan.erase(unique(Lisan.begin(), Lisan.end()), Lisan.end());vector<vi> user2req(K + 1, vi());for(auto & p : Req){p.second = lower_bound(Lisan.begin(), Lisan.end(), p.second) - Lisan.begin();user2req[p.first].emplace_back(p.second);}User2Gain.assign(K + 1, vi());for(int i=1;i<=K;++i){proc(user2req[i], User2Gain[i]);// cout << i << ":";// for(auto j : User2Gain[i]){// cout << " " << M - j;// }// cout << endl;}D.assign(K + 1, vi(N + 1, 0));int total = 0;for(int user=1;user<=K;++user){const auto & gain = User2Gain[user];total += gain.size() - 1;if(total >= N) total = N;for(int space=0;space<=total;++space){int ava = min((int)gain.size() - 1, space);auto & tmp = D[user][space];for(int i=0;i<=ava;++i){tmp = max(tmp, D[user-1][space-i] + gain[i]);}}}int ans = M * K;const auto & vec = D[K];for(int i=0;i<=N;++i){ans = min(ans, M * K - vec[i]);}return ans;
}int main(){
#ifndef ONLINE_JUDGEfreopen("z.txt", "r", stdin);
#endifios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(0);int nofkase = 1;cin >> nofkase;while(nofkase--){cin >> N >> K >> M;Req.assign(M, {});for(auto & p : Req) cin >> p.first >> p.second;cout << proc() << "\n";}return 0;
}
强者6
差分加树状数组。
假设第 i i i个请求和第 j j j个请求是同一个页面,则 j j j有可能命中缓存。取决于 i , j i,j i,j之间不同页面种类的数量与缓存空间的大小关系。为方便论述,称不同页面种类的数量为间隔数。例如:
1 , 2 , 3 , 4 , 2 , 3 , 4 , 1 1,2,3,4,2,3,4,1 1,2,3,4,2,3,4,1
上述两个页面1之间的间隔数为3,所以当缓存空间大于3时,第二个页面1必然是命中的;否则必然有缺页中断。基于简单的贪心可知,如果缓存空间为 K K K时,某个 j j j请求会有缺页中断,则缓存空间更小时,必然也会有缺页中断。因此只需要对相邻的相等页面,求出间隔数即可。这是一个典型的树状数组应用。
令 A A A数组是页面请求数组, B B B是一个树状数组。pre[v]是数值v在数组 A A A中前一个最近的位置。则:
for i,v in A:求B[pre[v], v]之间的和,记作s, s就是一个间隔数, 令cnt[s] += 1将B[pre[v]] -= 1将B[i] += 1pre[v] = i
由此就得到了每一个间隔数出现的数量,根据此就能算出缺页数(注意到此时,页面是几其实已经不重要)。
计算间隔数应该是 O ( M log M ) O(M\log{M}) O(MlogM),根据间隔数计算 A n s Ans Ans应该是 O ( M ) O(M) O(M)。
#include <bits/stdc++.h>
using namespace std;#include <bits/extc++.h>
using namespace __gnu_pbds;using llt = long long;
using Real = double;
using vi = vector<int>;
using pii = pair<int, int>;struct FenwickTree{ // 树状数组using value_type = long long int;
using vec_type = vector<value_type>;int n;
vec_type c;FenwickTree() = default;static int lowbit(int x){return x & -x;}void init(int nn){this->c.assign((this->n=nn) + 1, 0);}void modify(int pos, value_type delta){for(int i=pos;i<=this->n;i+=lowbit(i)) this->c[i] += delta;
}value_type query(int pos)const{value_type ans = 0;for(int i=pos;i;i-=lowbit(i)) ans += this->c[i];return ans;
}value_type query(int s, int e)const{return this->query(e) - this->query(s - 1);}}Bt;int M;
vi A;
vi Ans;void proc(){ Bt.init(M);map<int, int> cnt;vi pre(1000000 + 1, 0);for(int p,v,i=0;i<M;++i){p = i + 1;v = A[i];if(pre[v]){Bt.modify(pre[v], -1);cnt[Bt.query(pre[v], p)] += 1;}else{cnt[M] += 1;} Bt.modify(pre[v] = p, 1);}Ans.assign(M + 1, 0);int sum = 0;int another = M;for(auto it=cnt.rbegin(),jt=++cnt.rbegin(),et=cnt.rend();jt!=et;++it,++jt){int last = it->first;int start = jt->first;sum += it->second;fill(Ans.begin() + start + 1, Ans.begin() + last + 1, sum);}cout << (Ans[0] = M);for(int i=1;i<=M;++i) cout << " " << Ans[i];cout << endl;
}int main(){
#ifndef ONLINE_JUDGEfreopen("z.txt", "r", stdin);
#endifios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(0);cin >> M;A.assign(M, {});for(auto & i : A) cin >> i;proc();return 0;
}
相关文章:

蓝桥杯算法赛第4场小白入门赛强者挑战赛
蓝桥杯算法赛第4场小白入门赛&强者挑战赛 小白1小白2小白3强者1小白4强者2小白5强者3小白6强者4强者5强者6 链接: 第 4 场 小白入门赛 第 4 场 强者挑战赛 小白1 直接用C内置函数即可。 #include <bits/stdc.h> using namespace std;#include <bits…...

【每日一题】6.LeetCode——轮转数组
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》|《数据结构与算法》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️ 🙏小杨水平有限,欢…...

Java编程练习之类的封装2
1.封装一个股票(Stock)类,大盘名称为上证A股,前一日的收盘点是2844.70点,设置新的当前值如2910.02点,控制台既要显示以上信息,又要显示涨跌幅度以及点数变化的百分比。运行效果如下:…...

Banana Pi BPI-R4开源路由器开发板快速上手用户手册,采用联发科MT7988芯片设计
介绍 Banana Pi BPI-R4 路由器板采用 MediaTek MT7988A (Filogic 880) 四核 ARM Corex-A73 设计,4GB DDR4 RAM,8GB eMMC,板载 128MB SPI-NAND 闪存,还有 2x 10Gbe SFP、4x Gbe 网络端口,带 USB3 .2端口,M.2…...
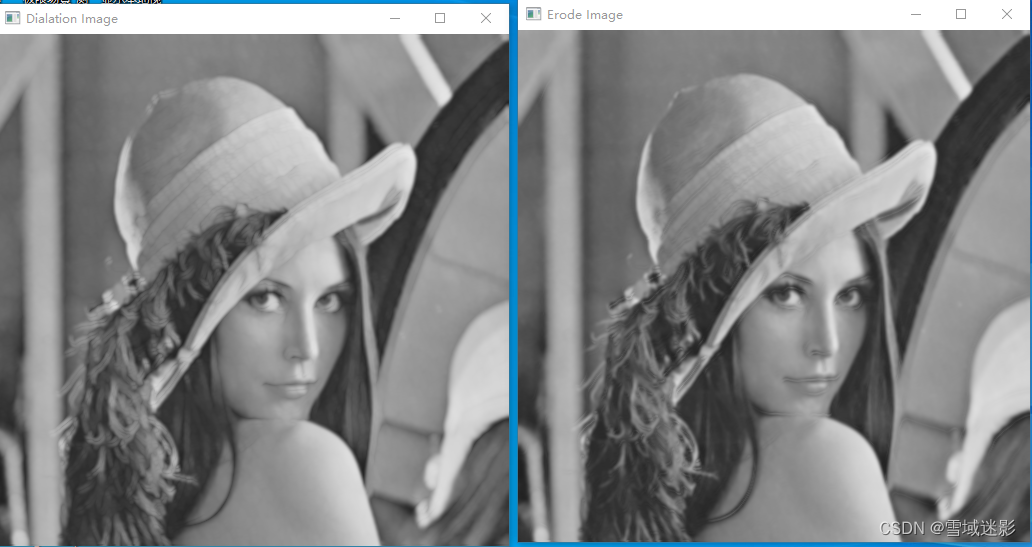
C#使用OpenCvSharp4库中5个基础函数-灰度化、高斯模糊、Canny边缘检测、膨胀、腐蚀
C#使用OpenCvSharp4库中5个基础函数-灰度化、高斯模糊、Canny边缘检测、膨胀、腐蚀 使用OpenCV可以对彩色原始图像进行基本的处理,涉及到5个常用的处理: 灰度化 模糊处理 Canny边缘检测 膨胀 腐蚀 1、测试图像lena.jpg 本例中我们采用数字图像处…...

蓝桥杯2024/1/31----第十届省赛题笔记
题目要求: 1、 基本要求 1.1 使用大赛组委会提供的国信长天单片机竞赛实训平台,完成本试题的程序设计 与调试。 1.2 选手在程序设计与调试过程中,可参考组委会提供的“资源数据包”。 1.3 请注意: 程序编写、调试完成后选手…...
CANopen转Profinet网关实现原理与CANopen主站配置方法
CANopen转Profinet网关(XD-COPNm20)具有Profinet从站功能的设备。CANopen是一种通用的工业网络协议,而Profinet是以太网上的一种通信协议,两者在工业自动化领域具有广泛的应用。CANopen转Profinet网关的主要作用是实现CANopen设备…...

Mysql单行函数练习
数据表 链接:https://pan.baidu.com/s/1dPitBSxLznogqsbfwmih2Q 提取码:b0rp --来自百度网盘超级会员V5的分享 单行函数练习 单行函数(一行数据返回一个结果) #1.显示系统时间(注:日期时间) #2.查询员工工号,姓名,工资以及提高百分之20后的结果(new…...

C++ 11新特性之完美转发
概述 在C编程语言的演进过程中,C 11标准引入了一系列重大革新,其中之一便是“完美转发”机制。这一特性使得模板函数能够无损地传递任意类型的实参给其他函数或构造函数,从而极大地增强了C在泛型编程和资源管理方面的灵活性与效率。 完美转发…...
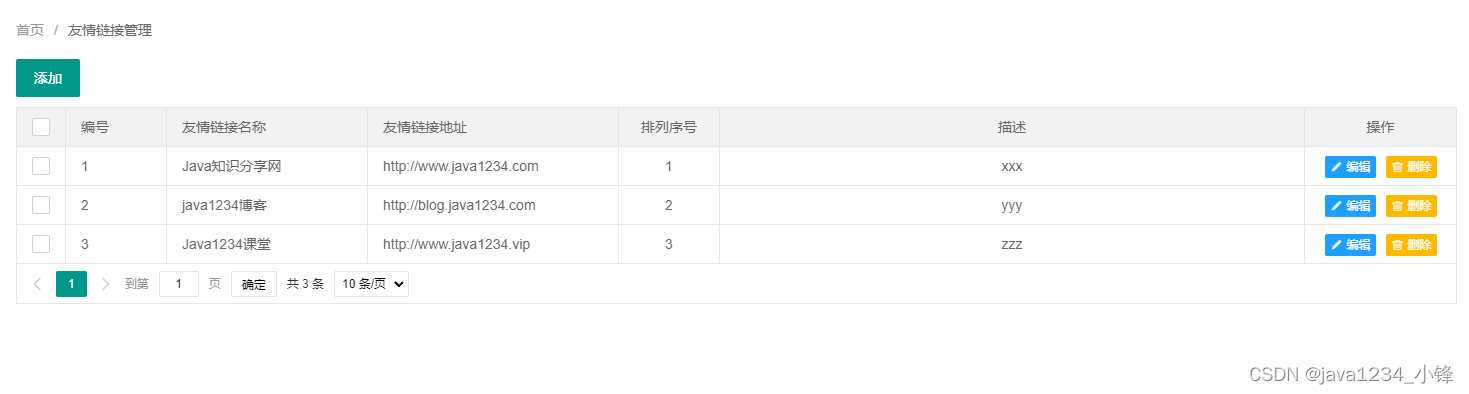
python222网站实战(SpringBoot+SpringSecurity+MybatisPlus+thymeleaf+layui)-友情链接管理实现
锋哥原创的SpringbootLayui python222网站实战: python222网站实战课程视频教程(SpringBootPython爬虫实战) ( 火爆连载更新中... )_哔哩哔哩_bilibilipython222网站实战课程视频教程(SpringBootPython爬虫实战) ( 火…...
【百度Apollo】探索自动驾驶:深入解析Apollo开放平台架构的博客指南
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《linux深造日志》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! ⛳️ 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下…...
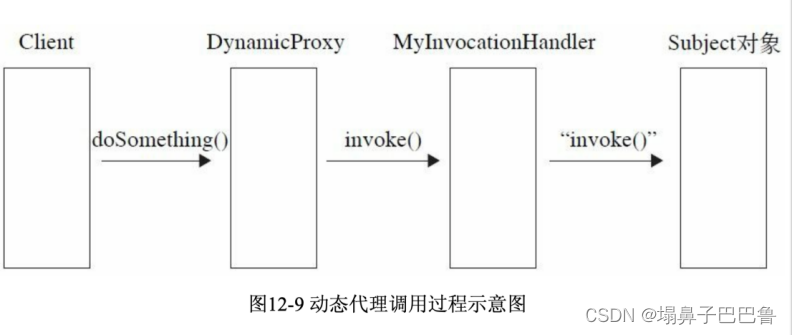
代理模式详解(重点解析JDK动态代理)
- 定义 在解析动态代理模式之前,先简单看下整个代理模式。代理模式分为普通代理、强制模式、动态代理模式。其中动态代理模式主要实现方式为Java JDK提供的JDK动态代理,第三方类库提供的,例如CGLIB动态代理。 代理模式就是为其他对象提供一种…...

【大厂AI课学习笔记】1.3 人工智能产业发展(2)
(注:腾讯AI课学习笔记。) 1.3.1 需求侧 转型需求:人口红利转化为创新红利。 场景丰富:超大规模且多样的应用场景。主要是我们的场景大,数据资源丰富。 抗疫加速:疫情常态化,催生新…...

【Python】一个简单的小案例:实现将两张图片合并为一张
使用时保证已经安装了opencv-python import cv2bg "BG.jpg" # 背景图名称 fg "FG.jpg" # 前景图名称 output_filename "new.jpg" # 合成后图片名称img_bg cv2.imread(bg) # 读取背景图 img_fg cv2.imread(fg) # 读取前景图# 读取背景…...

不同的强化学习模型适配与金融二级市场的功能性建议
DQN ES DDPG A2C TD3 SAC QMIX MADDPG PPO CQL IMPALA 哪个模型适合进行股票操作 在考虑使用哪种模型进行股票操作时,需要考虑模型的特点、适用场景以及实现复杂度等因素。以下是对您列出的几种强化学习模型的简要概述,以帮助您做出选择: DQ…...
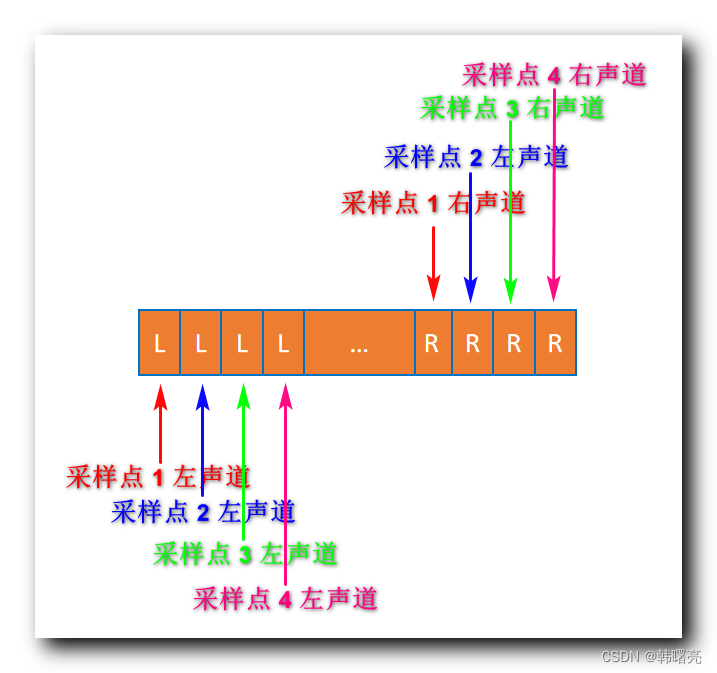
【音视频原理】音频编解码原理 ③ ( 音频 比特率 / 码率 | 音频 帧 / 帧长 | 音频 帧 采样排列方式 - 交错模式 和 非交错模式 )
文章目录 一、音频 比特率 / 码率1、音频 比特率2、音频 比特率 案例3、音频 码率4、音频 码率相关因素5、常见的 音频 码率6、视频码率 - 仅做参考 二、音频 帧 / 帧长1、音频帧2、音频 帧长度 三、音频 帧 采样排列方式 - 交错模式 和 非交错模式1、交错模式2、非交错模式 一…...

spring常用语法
etl表达式解析 if (rawValue ! null && rawValue.startsWith("#{") && entryValue.endsWith("}")) { // assume its spel StandardEvaluationContext context new StandardEvaluationContext(); context.setBeanResolver(new Be…...
【计算机毕业设计】128电脑配件销售系统
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...
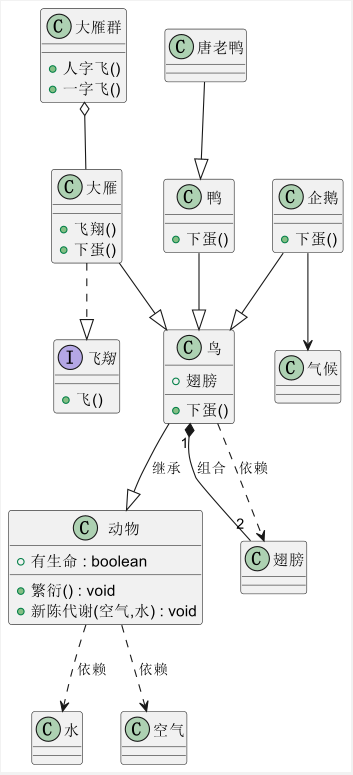
换个思维方式快速上手UML和 plantUML——类图
和大多数朋友一样,Jeffrey 在一开始的时候也十分的厌烦软件工程的一系列东西,对工程化工具十分厌恶,觉得它繁琐,需要记忆很多没有意思的东西。 但是之所以,肯定有是因为。对工程化工具的不理解和不认可主要是基于两个逻…...

策略模式+SpringBoot接口,一个接口实现接收的数据自动分流处理
策略模式 定义了算法族,分别封装起来,让它们之间可以互相替换,此模式让算法的变化,不会影响到使用算法的客户。策略模式的精髓就在于将经常变化的一点提取出来,单独变成一类,并且各个类别可以相互替换和组合。 1、策略接口 CalculationStrategy //算数 public interface…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
