【ChatGPT】文本向量化与余弦相似度:揭开文本处理的神秘面纱(5)
1、引言
在这个数字化的时代,我们每天都会面对大量的文本信息,从社交媒体到新闻报道,文本无处不在。但是,计算机要如何理解和处理这些文字呢?本文将为大家揭开其中的一些奥秘,详细解释文本向量化的概念,以及通过余弦相似度如何计算文本之间的相似度。
说白了,就是把文字、图片或其他东西变成一串数字,然后通过计算这些数字的距离来找相似的东西。这样做有啥好处呢?能够让搜索更快、更准确,而且在很多地方都能派上用场。
2、什么是向量?
先别怕,我们来聊聊向量。在这里,向量就是一种数学工具,它可以帮助我们在计算机中表示信息。你可以把向量看作是一个有序的数字列表,就像在坐标系中标出的点。在计算机科学领域,向量通常被用来表示数据的多维空间中的点。例如,一个二维向量 v 可以表示平面上的一个点,其中 v=[x, y]。
3、文本向量化方法
原理其实挺简单的。就是把东西转化成数字的形式,然后把这些数字放在一个虚拟的空间里。相似的东西在这个虚拟空间里靠得比较近,不相似的就远一点。这样,只要计算一下距离,就能找到相似的东西了。
1. 词袋模型
先别被名词吓到,词袋模型其实很简单。它把一段文字看成是一个袋子,里面装满了各种词汇。每个文档(比如一篇文章)都可以被表示为一个向量,向量的每个元素表示相应词汇在文档中出现的次数。
比如说,对于文本 “机器学习是人工智能的分支。”,我们可以得到一个向量表示: [1,1,1,1,1][1,1,1,1,1]。
2. Word Embeddings
再来看看Word Embeddings,这个名词听起来高级,但实际上很有趣。它通过将每个单词映射为一个实数向量,捕捉到了单词之间的关系。比如, “机器学习是人工智能的分支。” 可以被表示为向量: [0.23,0.45,−0.12,0.67,0.89][0.23,0.45,−0.12,0.67,0.89]。
4、余弦相似度计算
好了,现在我们有了文本的向量表示,接下来就是如何计算它们的相似度。这时候登场的就是余弦相似度了。这是一种衡量两个向量相似性的方法,通过计算夹角的余弦值来得出相似度。假设下面三个文本词向量分别是(为了演示简单,使用的是二维向量):
机器学习是人工智能的分支(用A表示)。对应的向量为 [1.5,1.5],
人工智能的重要分支是机器学习(用B表示)。对应的向量为 [2.0,1.0],
天气预报说明天可能会下雨(用C表示)。对应的向量为 [-1.0,-0.5]
计算这三个文本之间的相似度,如下图示:
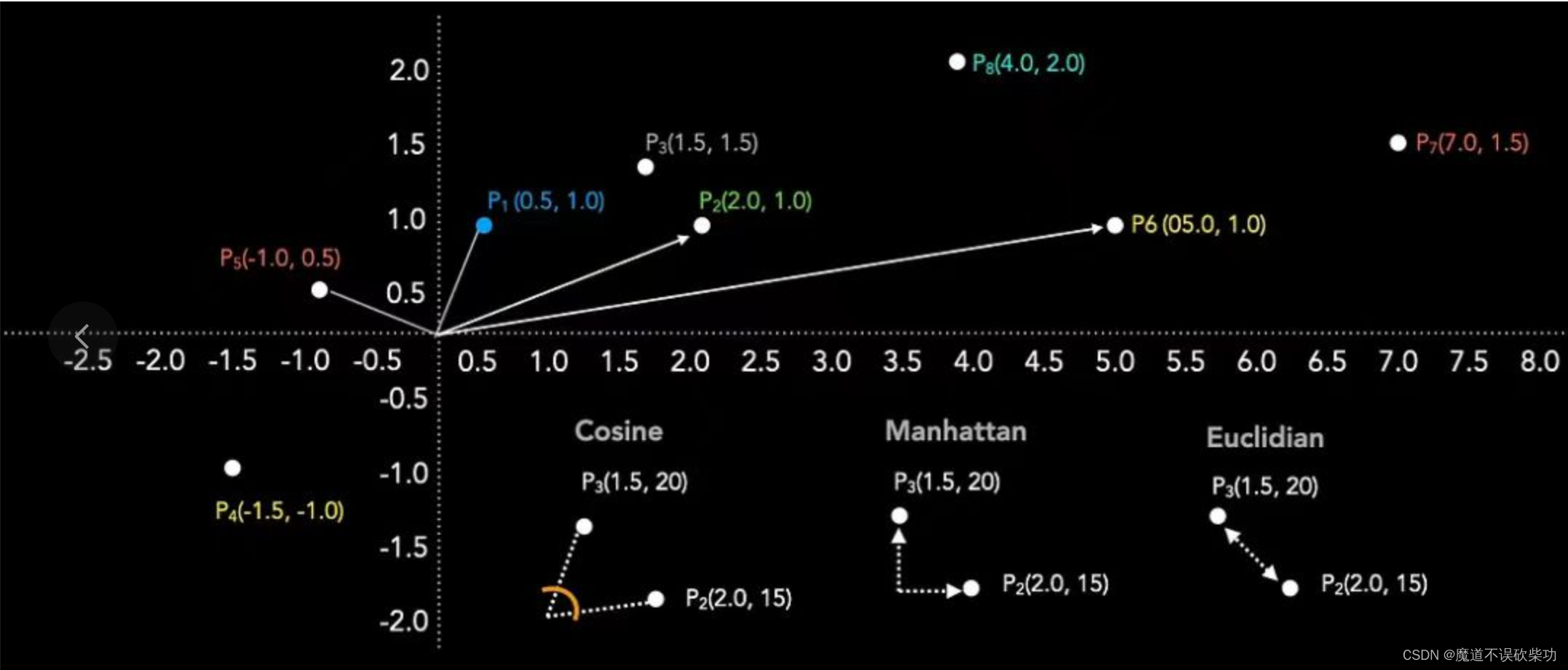
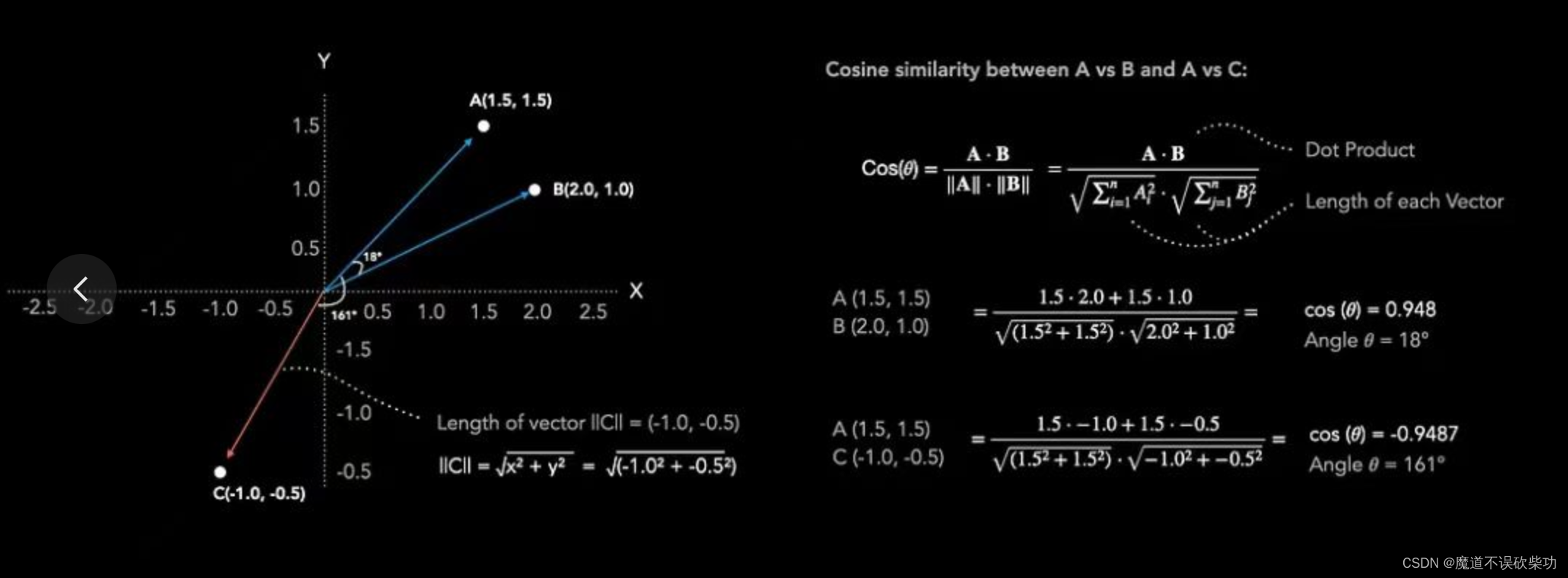
我们可以计算余弦相似度,得到A与B的余弦约为0.948,A与C的余弦约为-0.9487.。因为余弦0.948越靠近1,说明A与B文本越相似。从中文意思理解也是符合常理语义的。
5、文本向量化的应用场景
现在你可能会想,这些向量有什么用呢?原来,它们可以用于各种各样的应用:
- 推荐系统: 帮助计算机理解用户兴趣,实现个性化推荐。
- 情感分析: 通过分析文本的向量,计算机能够判断情感是正面还是负面。
- 文本相似度计算: 通过比较文本向量,找到相似的文本,用于搜索或者分类。
- 图像处理: 将图像特征表示为向量,实现图像检索等功能。
6、总结
文本向量化和余弦相似度为我们打开了处理文本数据的大门。通过这些方法,计算机能够更好地理解和利用文字信息。无论是在推荐系统、情感分析,还是在搜索引擎中,文本向量化都扮演着重要的角色。希望通过这篇博客,你对这些概念有了更清晰的认识。让我们一起迈向文本处理的新世界吧!
相关文章:

【ChatGPT】文本向量化与余弦相似度:揭开文本处理的神秘面纱(5)
1、引言 在这个数字化的时代,我们每天都会面对大量的文本信息,从社交媒体到新闻报道,文本无处不在。但是,计算机要如何理解和处理这些文字呢?本文将为大家揭开其中的一些奥秘,详细解释文本向量化的概念&am…...
计算机中丢失mfc100u.dll怎么解决,详细解析mfc100u.dll丢失的解决方法
遭遇“无法找到mfc100u.dll”的错误不必过分担忧,这是一个普遍现象。许多用户在启动某些软件或游戏的时候可能会碰到这样的情况。通常,这个错误信息表明你的计算机系统中缺失了一个关键的动态链接库(DLL)文件,它可能会妨碍应用程序的顺利启动…...
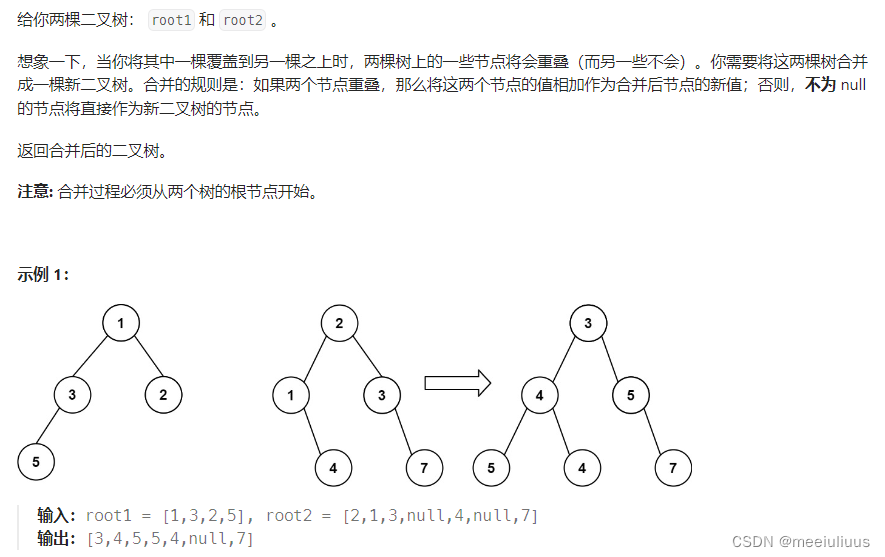
代码随想录 Leetcode617.合并二叉树
题目: 代码(首刷看解析 2024年1月31日): class Solution { public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if (!root1) return root2;if (!root2) return root1;root1->val root2->val;root1->left mergeTree…...

知识价值1-github站点域名
github如果访问不上,有一个办法是hosts映射: github.com x.x.x.x github.global.ssl.fastly.net y.y.y.y assets-cdn.github.com z.z.z.z1 assets-cdn.github.com z.z.z.z2 assets-cdn.github.com z.z.z.z3 assets-cdn.github.com z.z.z.z3 那这几个域名…...

【PyRestTest】进行Benchmarking测试
PyRestTest支持通过Curl请求本身收集比较差的网络环境下的性能指标。 基准测试:它们扩展了测试中的配置元素,允许你进行相似的REST调用配置。然而,它们不对HTTP响应情况进行验证,它只收集指标数据。 下列选项被指定用于benchmar…...
cocos creator 调用预设体Prefab中的方法(调用另一个节点的方法)
调用预设体中的方法 通过cc.instantiate(this.star)创建这个预设体实例这个star预设体中添加了一个脚本组件star.ts 获取到这个脚本组件star.getComponent(‘star’).test(),并调用其中的test()方法同理可以用该方式像另一个节点中传值 //星星预设体property(cc.Pr…...

Spring 学习2 --基于xml管理Bean
1、xml管理Bean <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://www.springfr…...

Java数组遍历深度解析
数组是Java编程中一种非常重要的数据结构,它用于存储相同类型的多个元素。在实际应用中,我们经常需要遍历数组中的所有元素,以进行相应的操作。理解数组的遍历方法对于编写高质量的代码至关重要。本文将深入探讨Java中的数组遍历方法。 一、…...
海洋鱼类检测7种YOLOV8NANO
【免费】海洋鱼类检测,7种类型,YOLOV8训练,转换成ONNX,OPENCV调用资源-CSDN文库 采用YOLOV8NANO训练模型,得到PT模型,然后转换成ONNX,供OPENCV的DNN调用,摆脱PYTORCH依赖,…...

Vue2组件注册:全局组件和局部组件
在Vue 2 中,你可以使用全局注册和局部注册两种方式注册组件。以下是两种方式的示例: • 全局注册 全局注册的组件可以在整个应用中使用,适用于高频的通用组件。 // 在 main.js 或者入口文件中 import Vue from vue import App from ./App.v…...

AD24-原理图与PCB交互设置及PCB常用快捷键汇总
一、原理图与PCB交互设置 1、在原理图页,工具-交叉选择模式 2、设置完成后。在原理图页选择器件,然后再PCB页也会相应被选中 3、一般将网络与Pin脚的勾去掉 4、整齐排列 5、TC:查找网络、器件、Pin脚 二、PCB常用快捷键汇总...
CTF-WEB进阶与学习
PHP弱类型 在进行比较的时候,会先判断两种字符串的类型是否相等,再比较 在进行比较的时候,会先将字符串类型转化成相同,再比较 如果比较一个数字和字符串或者比较涉及到数字内容的字符串,则字符串会被转换成数值 并且…...
C++初阶 类和对象(补充)
目录 一、友元 1.1什么是友元? 1.2如何使用友元? 1.3使用友元 1.4使用友元注意事项 二、初始化列表 2.1什么是初始化列表? 2.2为什么要有初始化列表? 2.3使用初始化列表 2.4注意事项 一、友元 1.1什么是友元? 友元是一…...

《HTML 简易速速上手小册》第2章:HTML 的标签和元素(2024 最新版)
文章目录 2.1 文本格式化标签(🎩✨📜 网页的“时尚搭配师”)2.1.1 基础示例:一篇博客的格式化2.1.2 案例扩展一:产品介绍页面2.1.3 案例扩展二:个人简历 2.2 链接和锚点(Ὢ…...

2024斋月大促跨境卖家准备指南
市场覆盖西欧、中东、东南亚、北非地区的跨境电商卖家注意了,2024年的斋月即将开启,较往年日期,今年提前了10天左右,斋月的第一天预测在3月11日星期一到来。 根据Google搜索数据可知,目前已经进入高频“斋月”搜索期&…...
【C++干货铺】哈希结构在C++中的应用
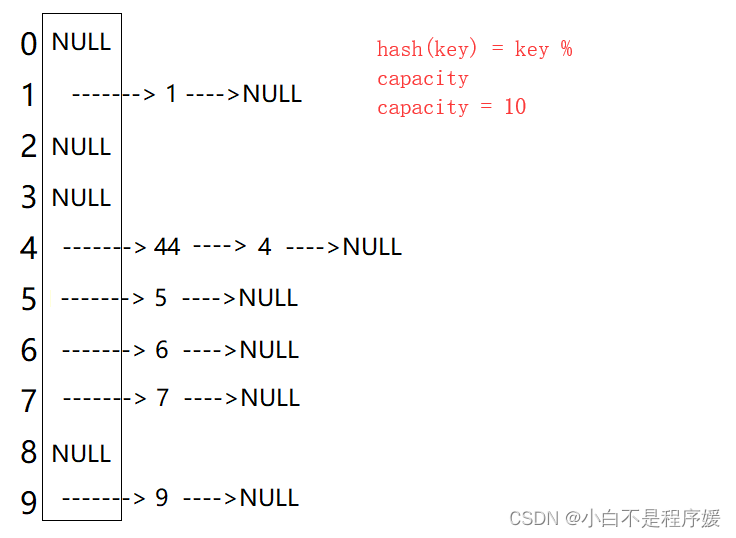
目录 unordered系列关联式容器 unordered_map unordered_map的接口说明 1.unordered_map的构造 2. unordered_map的容量 3. unordered_map的迭代器 4. unordered_map的元素访问 5. unordered_map的查询 6. unordered_map的修改操作 7. unordered_map的桶操作 底层结构 …...

蓝桥杯算法赛第4场小白入门赛强者挑战赛
蓝桥杯算法赛第4场小白入门赛&强者挑战赛 小白1小白2小白3强者1小白4强者2小白5强者3小白6强者4强者5强者6 链接: 第 4 场 小白入门赛 第 4 场 强者挑战赛 小白1 直接用C内置函数即可。 #include <bits/stdc.h> using namespace std;#include <bits…...

【每日一题】6.LeetCode——轮转数组
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》|《数据结构与算法》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️ 🙏小杨水平有限,欢…...

Java编程练习之类的封装2
1.封装一个股票(Stock)类,大盘名称为上证A股,前一日的收盘点是2844.70点,设置新的当前值如2910.02点,控制台既要显示以上信息,又要显示涨跌幅度以及点数变化的百分比。运行效果如下:…...

Banana Pi BPI-R4开源路由器开发板快速上手用户手册,采用联发科MT7988芯片设计
介绍 Banana Pi BPI-R4 路由器板采用 MediaTek MT7988A (Filogic 880) 四核 ARM Corex-A73 设计,4GB DDR4 RAM,8GB eMMC,板载 128MB SPI-NAND 闪存,还有 2x 10Gbe SFP、4x Gbe 网络端口,带 USB3 .2端口,M.2…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
