C语言数据结构之二叉树
少年恃险若平地
独倚长剑凌清秋
🎥烟雨长虹,孤鹜齐飞的个人主页
🔥个人专栏
🎥前期回顾-栈和队列
期待小伙伴们的支持与关注!!!
目录
树的定义与判定
树的定义
树的判定
树的相关概念
树的运用
树的表示
二叉树的概念及结构
二叉树的概念
二叉树的结构
特殊的二叉树
满二叉树
完全二叉树
二叉树的性质
二叉树的存储结构
顺序存储
链式存储
二叉树的遍历
二叉树结构定义
二叉树前序遍历
代码测试
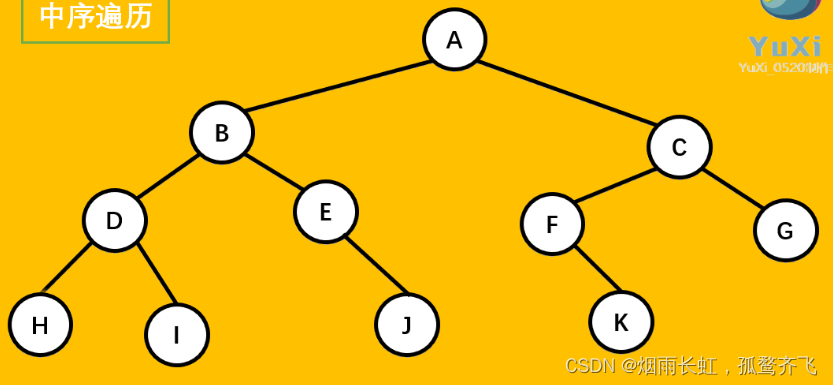
二叉树中序遍历
代码测试
二叉树后序遍历
代码测试
二叉树遍历口诀
二叉树的层序遍历
二叉树结点的个数
代码测试
二叉树叶子结点的个数
代码测试
二叉树的高度
代码测试
二叉树第k层节点个数
代码测试
二叉树查找值为x的节点
总结:

我们数据结构的前几章都是线性结构,而我们今天来学习非线性结构的数形结构--树
那什么是树形结构呢?
如图所示:根在下,叶朝上 的就是我们生活中的树
树的定义与判定
树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是 根朝上,而叶朝下 的树的定义
<1>有且仅有一个特殊的结点,称为根结点,根节点没有前驱结点 <2>除根节点外,其余结点被分成M(M>0)个互不相交的集合:T1、T2、… …、Tm
其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树
每棵子树的根结点有且只有一个前驱,可以有零个或多个后继
<3>树是递归定义的 树的判定
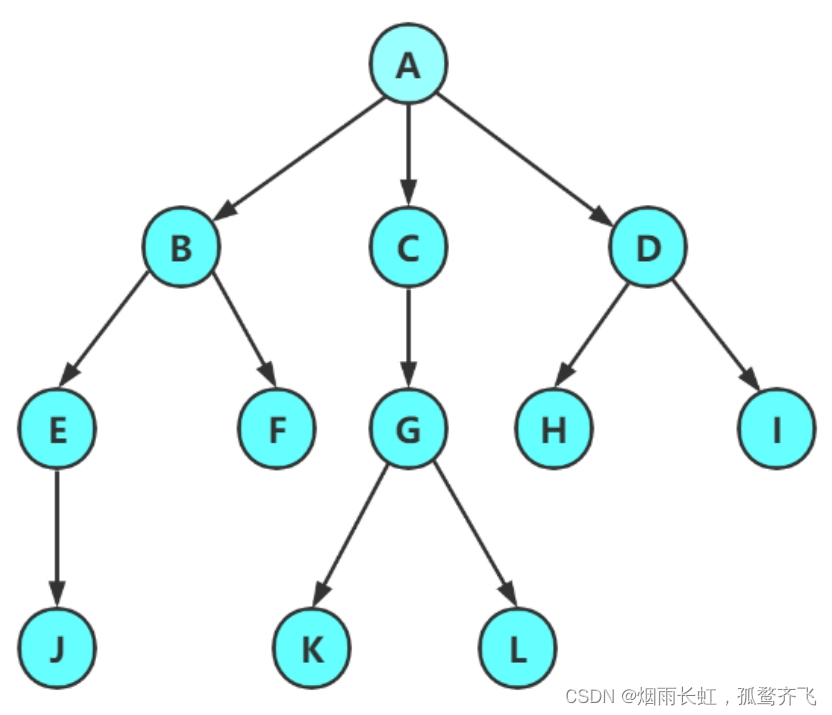
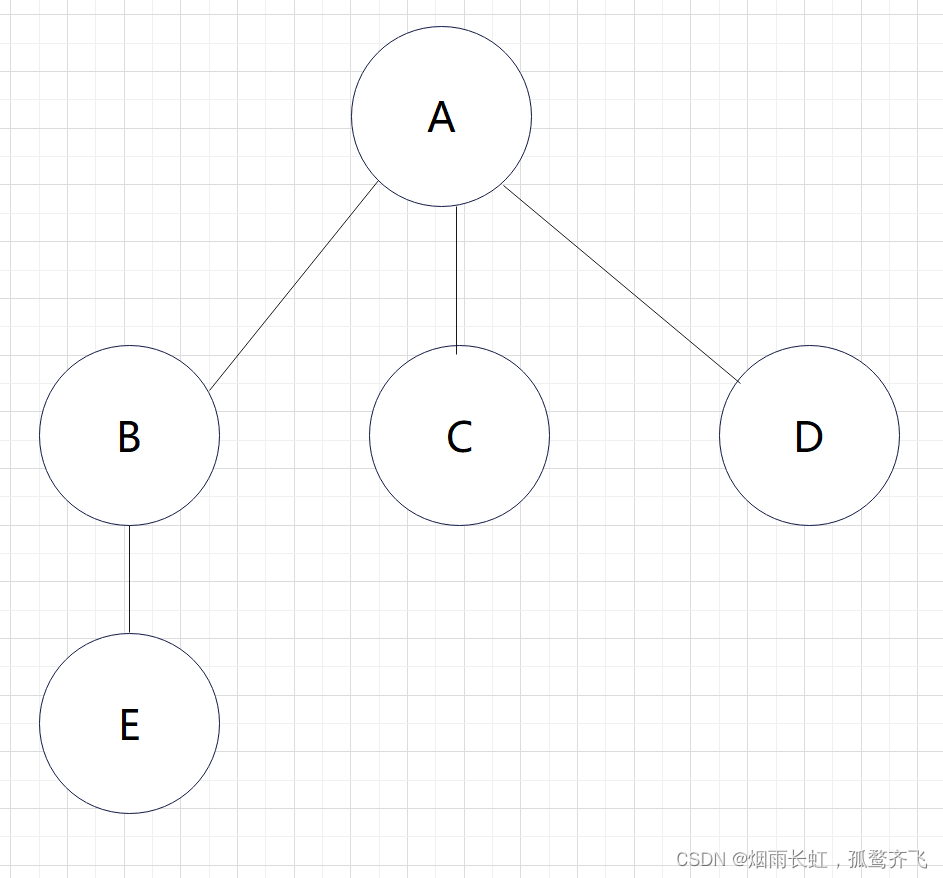
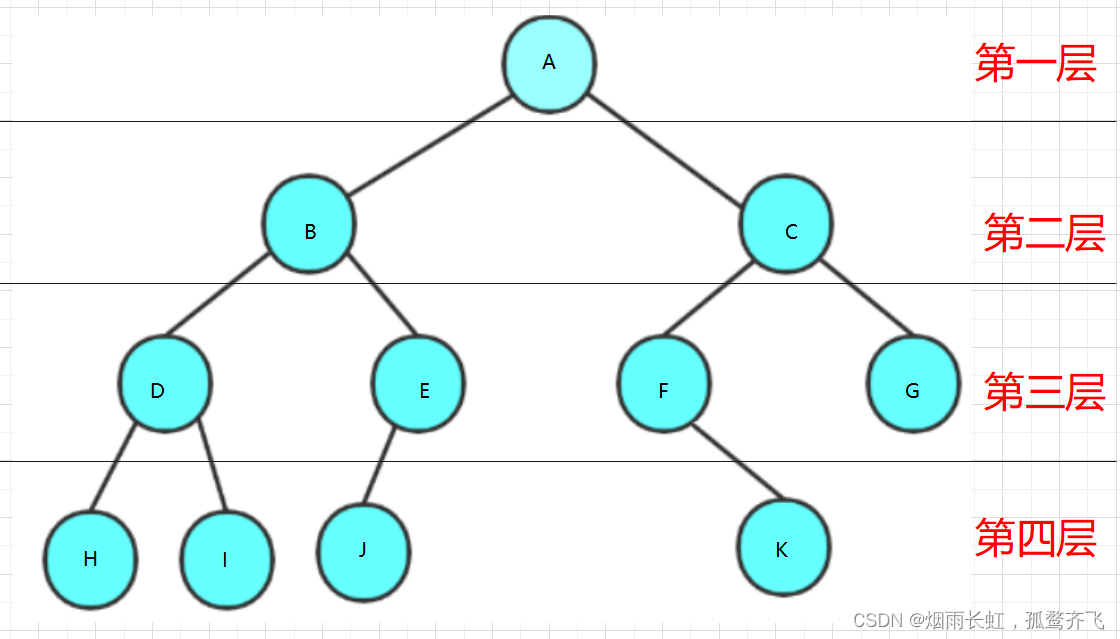
<1>树形结构中,子树之间不能有交集,否则就不是树形结构 <2>除了根节点以外,每个节点有且只有一个父节点 <3>一颗N节点的数有N-1条边 像以下的结构就是树形结构
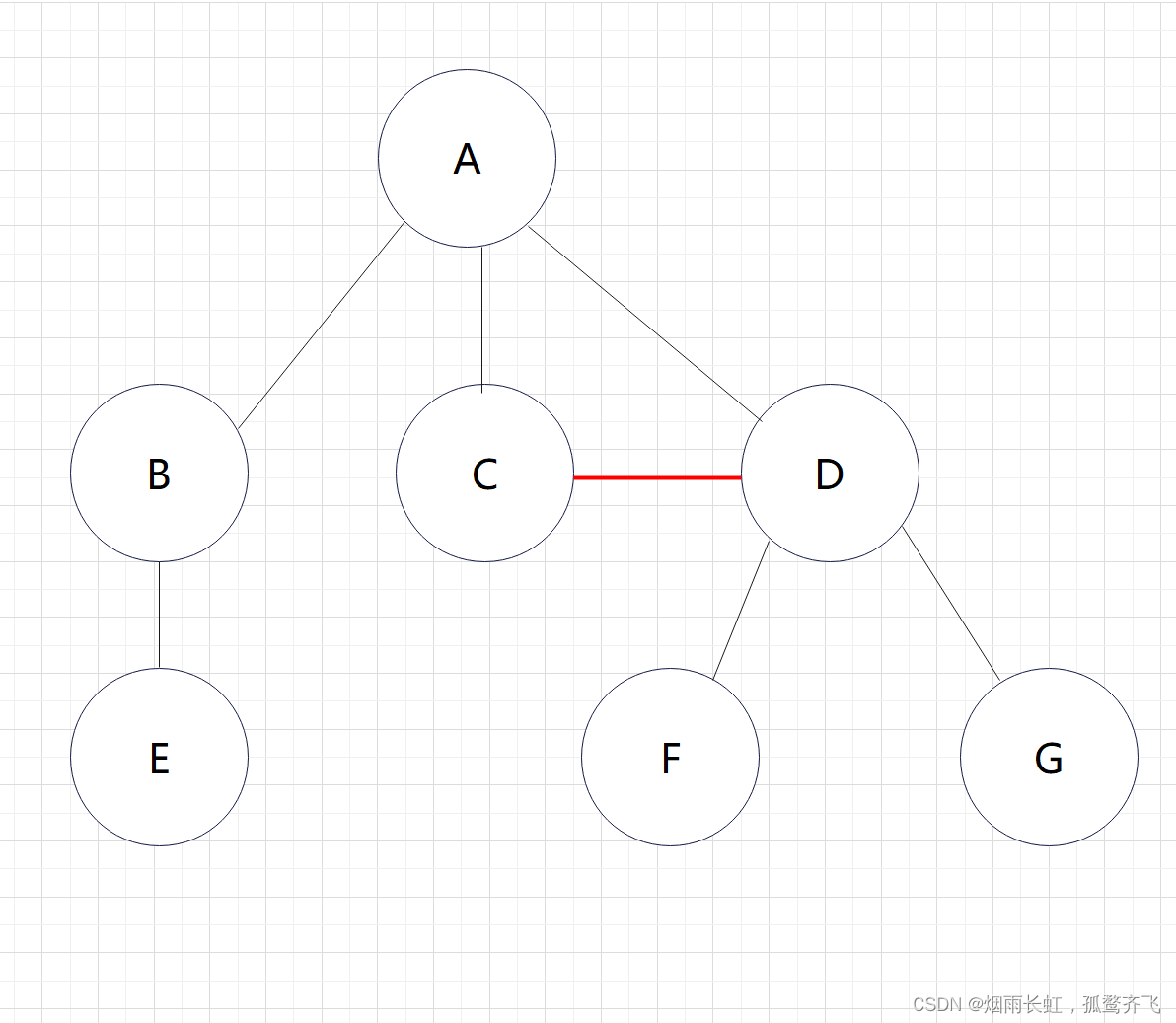
像以下 子树之间有交集 的结构就 不能 叫做树形结构
树的相关概念
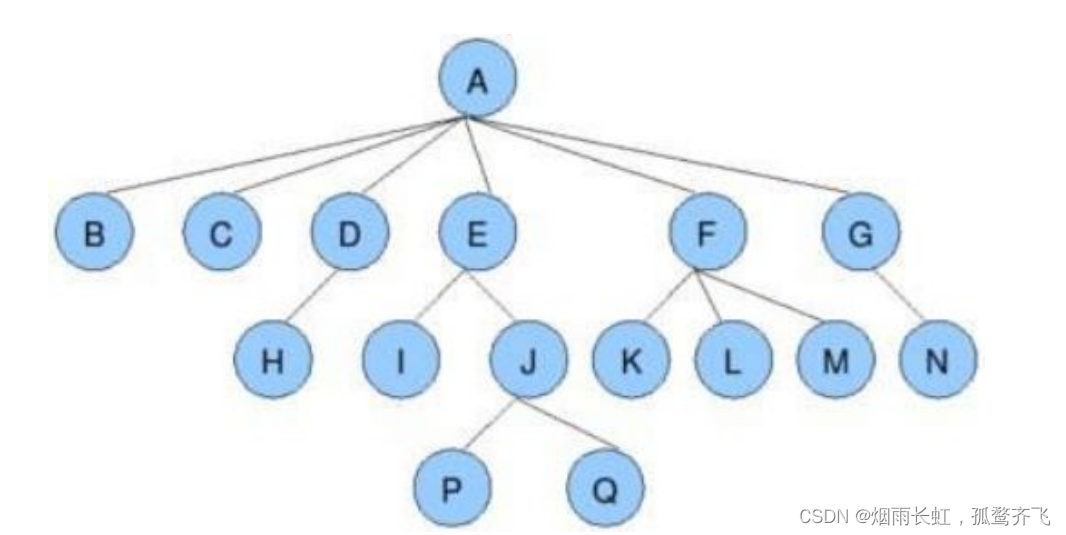
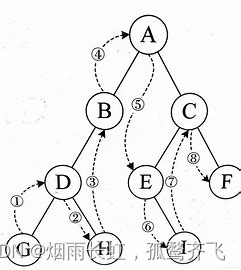
| 节点的度 : 一个节点含有的子树的个数称为该节点的度 ; 如上图: A 的节点度为 6 |
| 叶节点或终端节点 : 度为0的节点称为叶节点 ; 如上图: B 、 C 、 H 、 I... 等节点为叶节点 |
| 非终端节点或分支节点 : 度不为0的节点 ; 如上图: D 、 E 、 F 、 G... 等节点为分支节点 |
| 双亲节点或父节点 : 若一个节点含有子节点,则这个节点称为其子节点的父节点 ; 如上图: A 是 B 的父节点 |
| 孩子节点或子节点: 一个节点含有的子树的根节点称为该节点的子节点 ; 如上图: B 是 A 的孩子节点 |
| 兄弟节点 : 具有相同父节点的节点互称为兄弟节点 ; 如上图: B 、 C 是兄弟节点 |
| 树的度 : 一棵树中,最大的节点的度称为树的度 ; 如上图:树的度为 6 |
| 节点的层次 : 从根开始定义起,根为第1层,根的子节点为第2层,以此类推 |
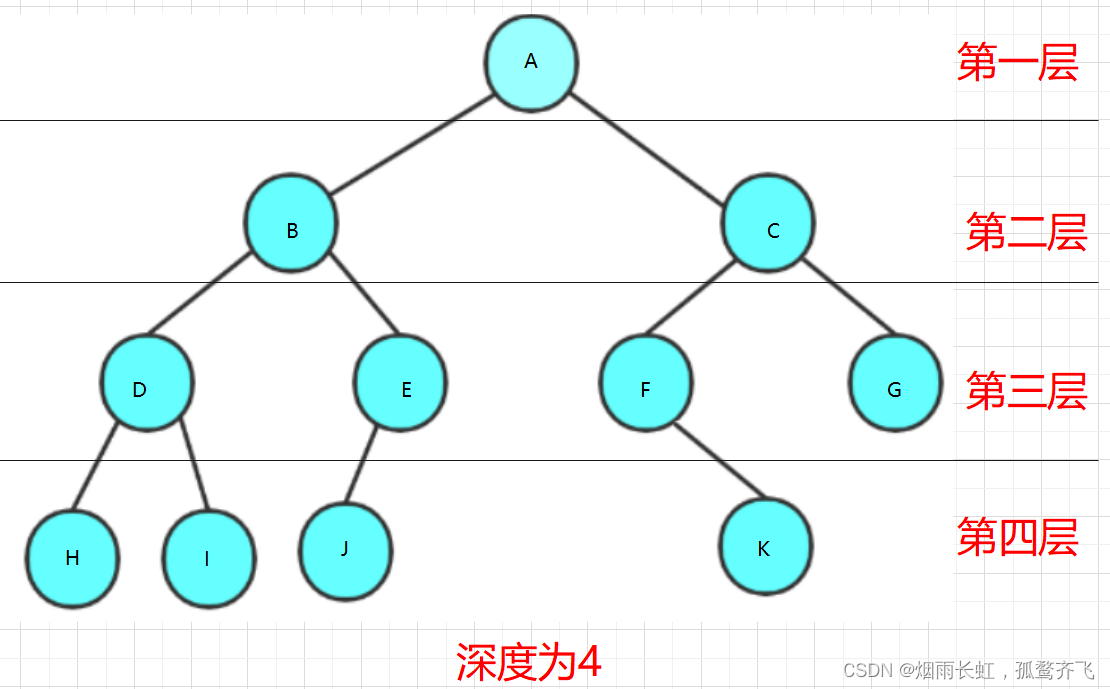
| 树的高度或深度 : 树中节点的最大层次 ; 如上图:树的高度为 4 |
| 堂兄弟节点 : 双亲在同一层的节点互为堂兄弟 ;如上图: H 、 I 互为兄弟节点 |
| 节点的祖先 : 从根到该节点所经分支上的所有节点 ;如上图: A 是所有节点的祖先 |
| 子孙 : 以某节点为根的子树中任一节点都称为该节点的子孙 ;如上图:所有节点都是 A 的子孙 |
| 森林 : 由m(m>0)棵互不相交的树的集合称为森林 |
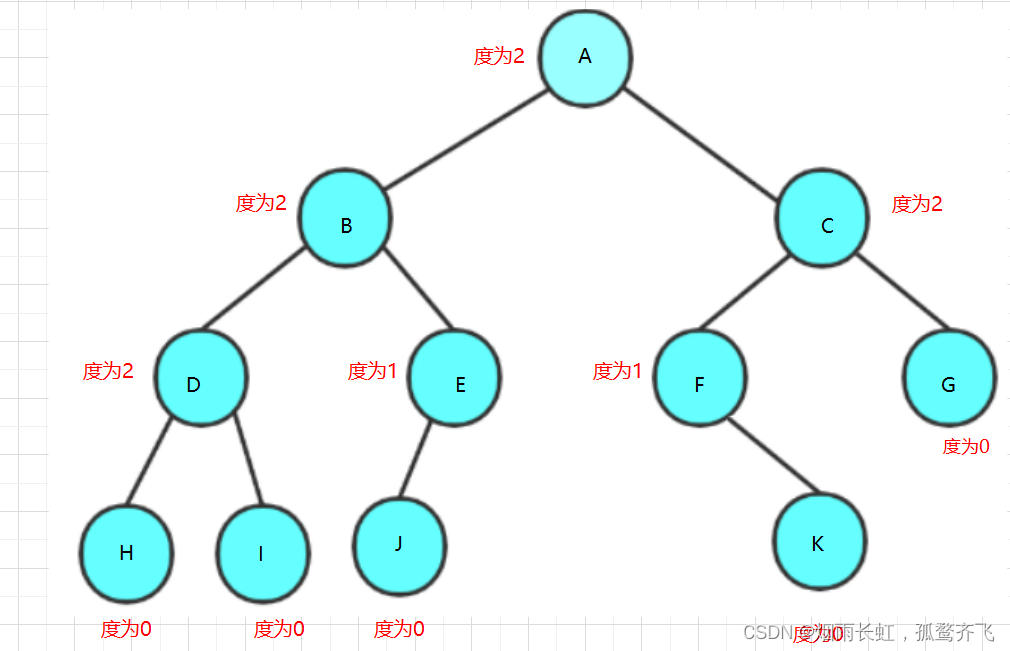
结点的度
结点拥有的子树数目称为结点的 度
结点层次
从 根开始定义 起,根为第一层,根的孩子为第二层,以此类推
树的深度
树中结点的 最大层次 数称为树的深度或高度
树的运用
以下是文件系统中目录的树的运用
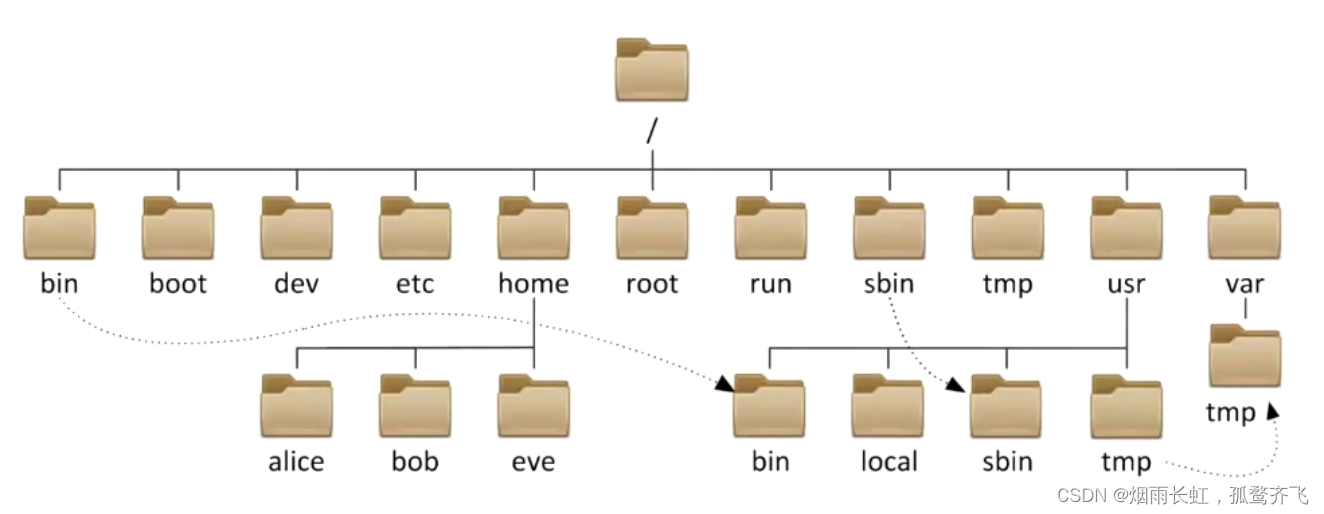
树的表示
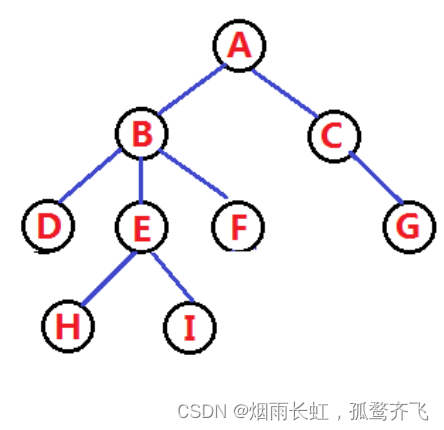
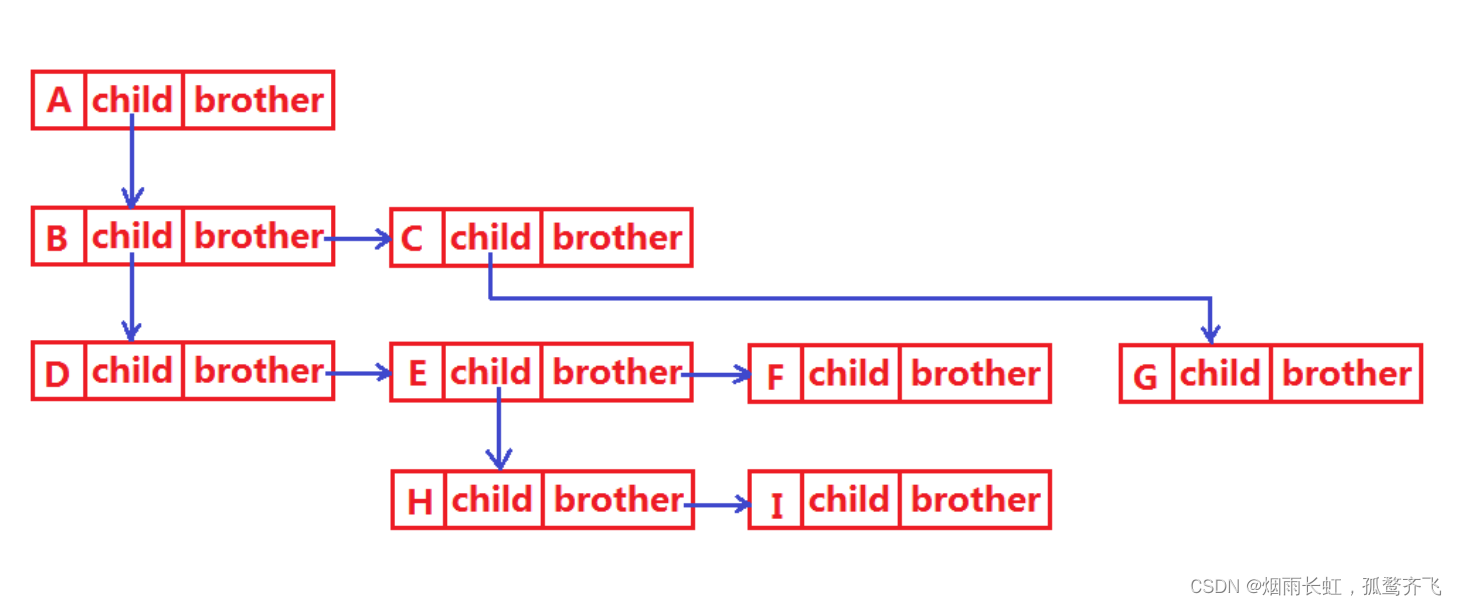
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了, 既然保存值域,也要保存结点和结点之间 的关系 ,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的 孩子兄弟表示法typedef char BTDataType;typedef struct BinaryTreeNode {struct BinaryTreeNode* left; // 第一个孩子结点struct BinaryTreeNode* right; // 指向其下一个兄弟结点BTDataType data; // 结点中的数据域 }BTNode;
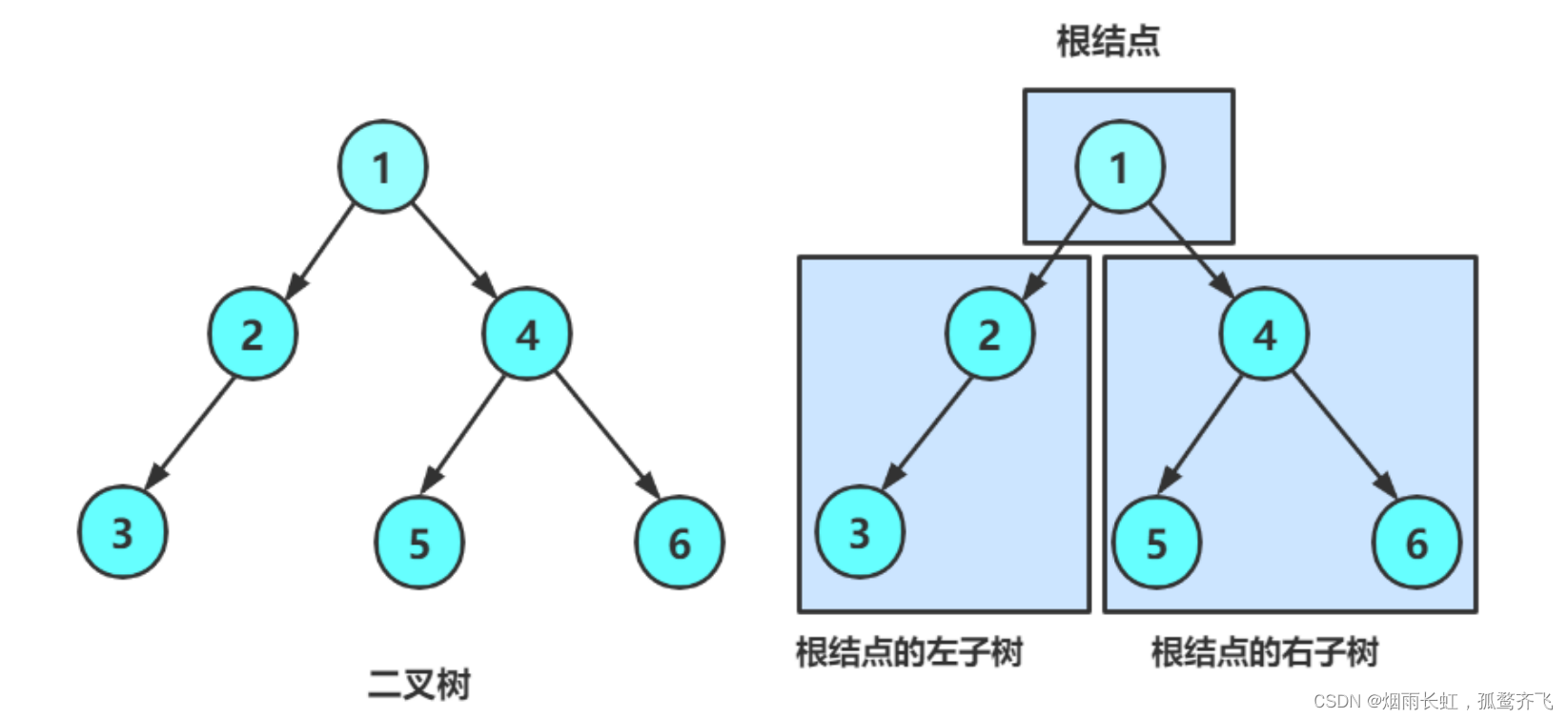
二叉树的概念及结构
二叉树的概念
二叉树(Binary Tree):是一个n(n>=0)个节点所构成的集合
该集合分为空树(n = 0),或者非空树
对于非空树:
<1>有且仅有一个 根节点 二叉树的结构
二叉树的五种基本形式: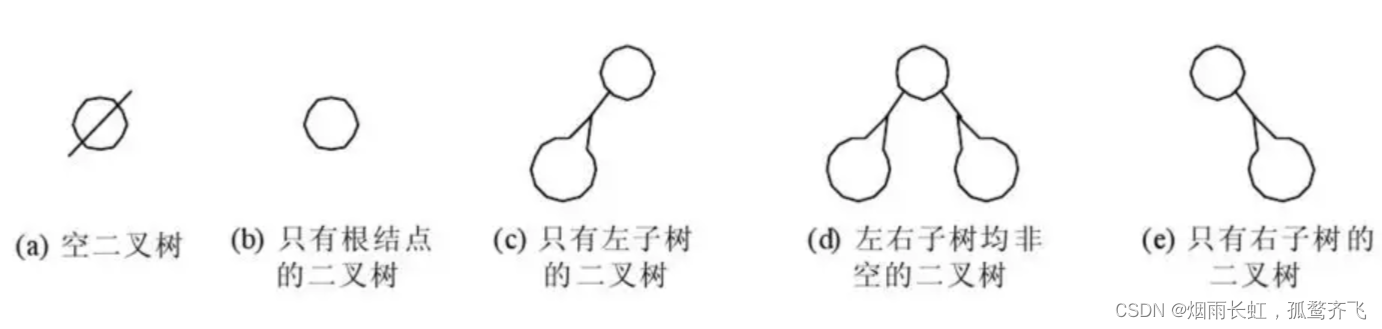
特殊的二叉树
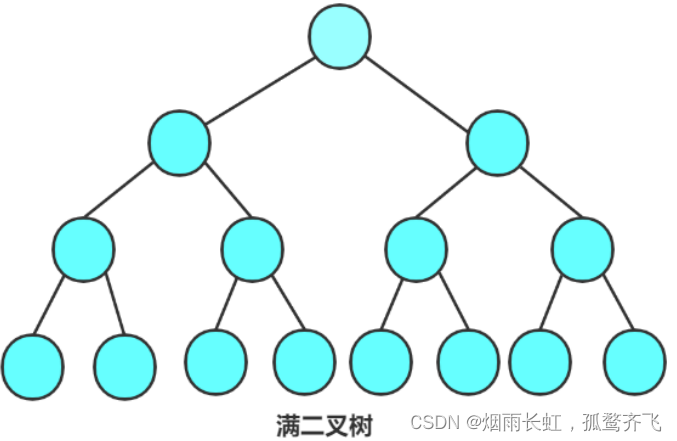
满二叉树
<1>满二叉树:一个二叉树,每层的结点数都达到最大值,则这个二叉树就是满二叉树
假设一颗满二叉树的高度为h
则总节点的个数:
N =
h =
每一个层的结点数都达到最大值 如果一个二叉树的层数为 K ,且结点总数是 2^k-1
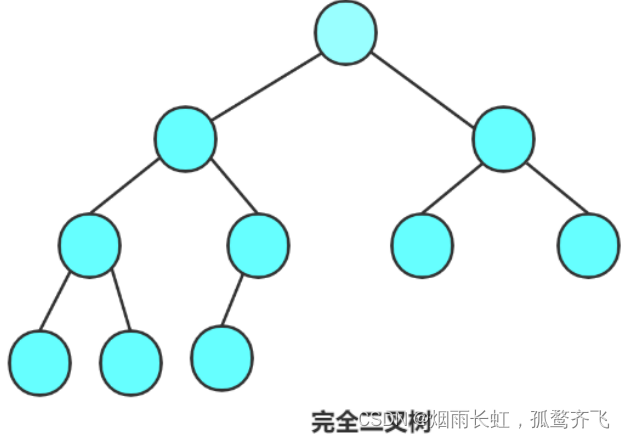
完全二叉树
<2>完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为 K 的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树
假设一颗完全二叉树的高度为h,高度为h的结点个数为x
则总节点的个数:
N =
h =
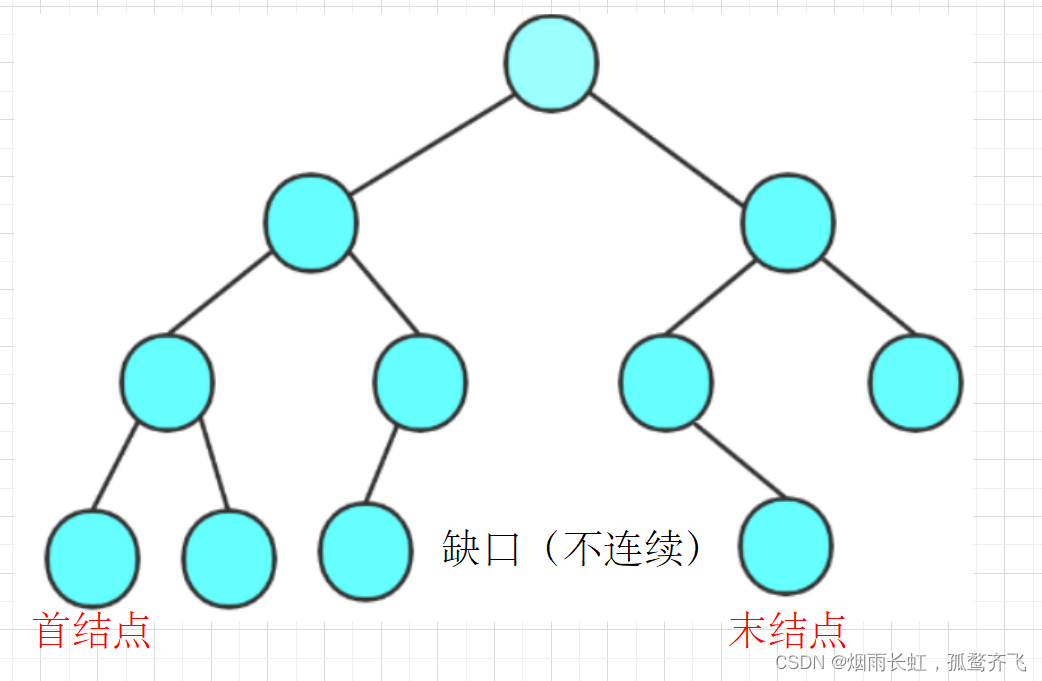
假设树的高度是h,前 h-1 层是 满 的 最后一行不满,但 从左往右是连续 的
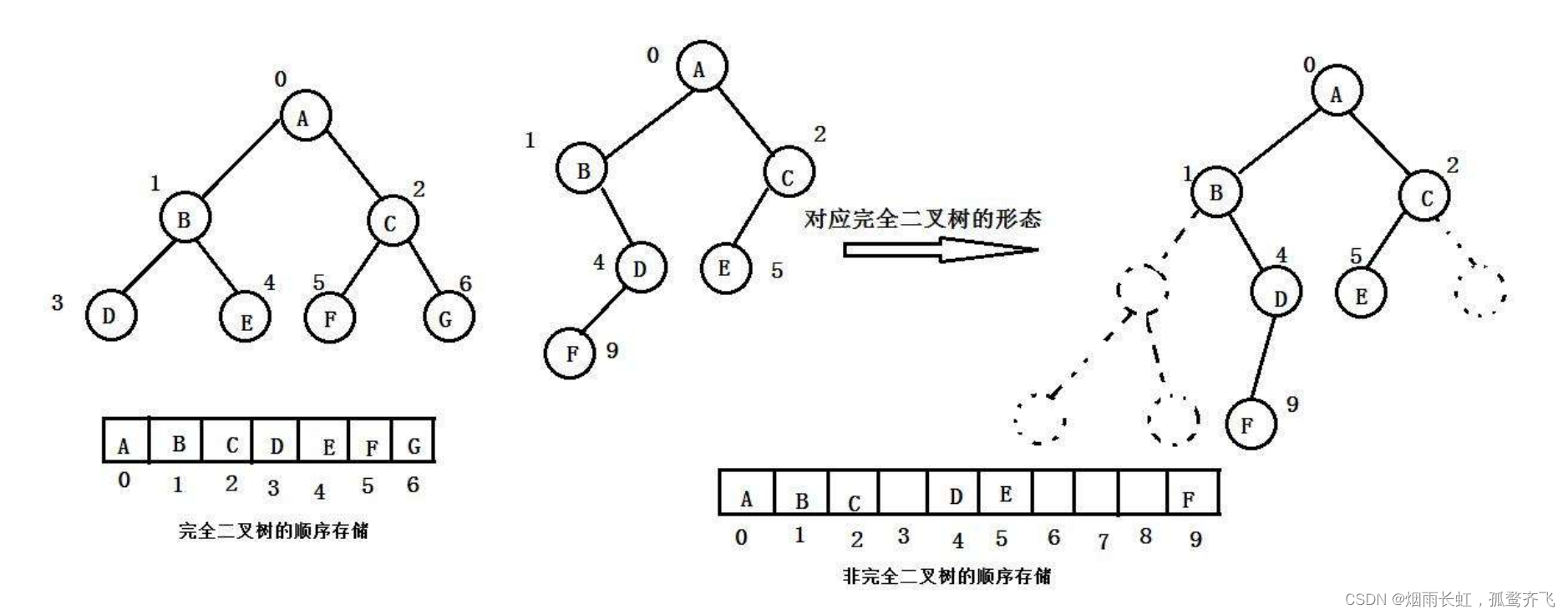
如上图所示就 非 完全二叉树:深度为 K 的节点中,从首结点到末结点中有 “ 缺口 ”
二叉树的性质
个结点
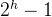

(1)若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点 (2)若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子 (3)若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构
顺序存储
顺序结构存储就是使用 数组来存储 ,一般使用数组 只适合表示完全二叉树 ,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。 二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树
链式存储
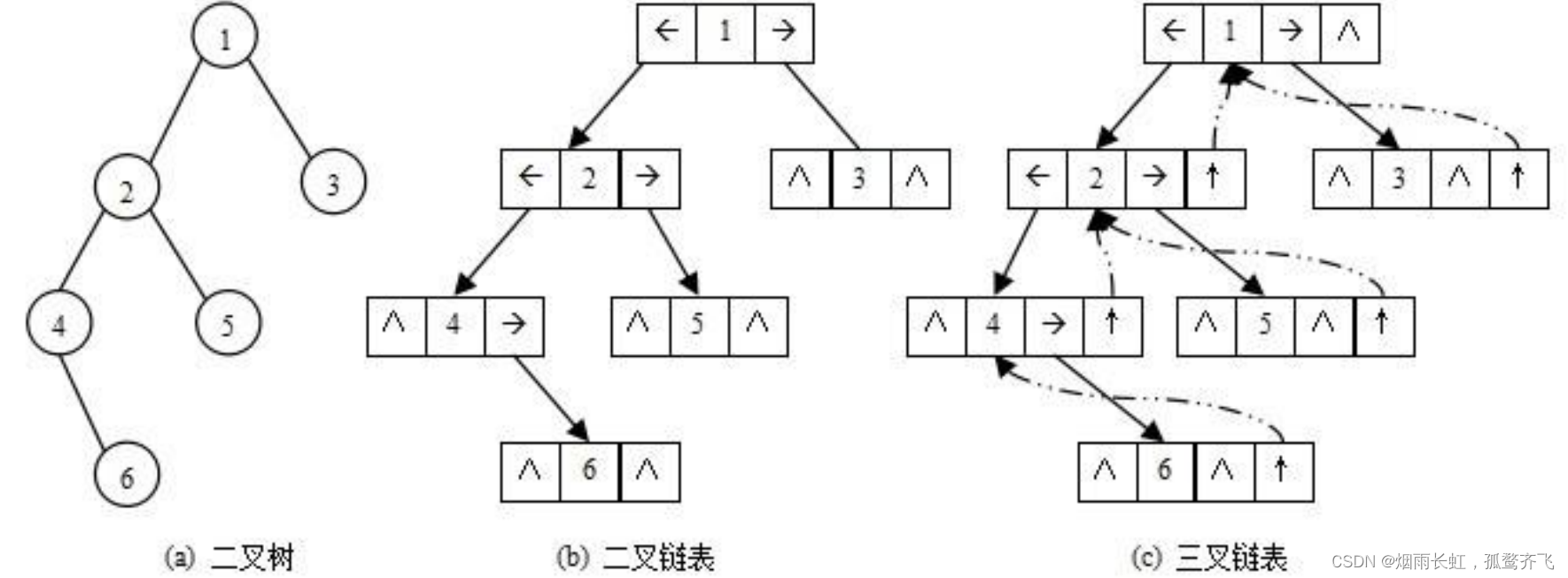
二叉树的链式存储结构是指,用 链表 来表示一棵二叉树,即用 链来指示元素的逻辑关系 。 通常的方法是链表中每个结点由 三个域 组成, 数据域和左右指针域 , 左右指针 分别用来给出该结点 左孩子和右孩子所在的链结点的存储地址 。链式结构又分为 二叉链和三叉链二叉树typedef char BTDataType;typedef struct BinaryTreeNode {struct BinaryTreeNode* left; //指向当前节点左孩子struct BinaryTreeNode* right; //指向当前节点右孩子BTDataType data; //节点中的数据域 }BTNode;三叉树typedef char BTDataType;typedef struct BinaryTreeNode {struct BinaryTreeNode* Parent; //指向当前节点的双亲struct BinaryTreeNode* left; //指向当前节点左孩子struct BinaryTreeNode* right; //指向当前节点右孩子BTDataType data; //节点中的数据域 }BTNode;
二叉树的遍历
二叉树遍历 (Traversal): 按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次 。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础
按照规则,二叉树的遍历有: 前序 / 中序 / 后序的递归结构遍历<1> 前序遍历 —— 访问根结点的操作发生在遍历其 左右子树之前<2>中序遍历 —— 访问根结点的操作发生在遍历其 左右子树之中<3>后序遍历 —— 访问根结点的操作发生在遍历其 左右子树之后
由于被访问的结点必是某子树的根
所以 N(Node )、 L(Left subtree )和 R(Right subtree)又可解释为 根、根的左子树和根的右子树NLR 、 LNR 和 LRN 分别又称为先根遍历、中根遍历和后根遍历
二叉树结构定义
typedef char BTDataType;typedef struct BinaryTreeNode {struct BinaryTreeNode* left; // 第一个孩子结点struct BinaryTreeNode* right; // 指向其下一个兄弟结点BTDataType data; // 结点中的数据域 }BTNode;
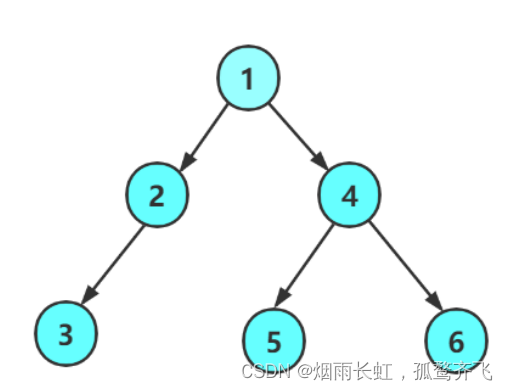
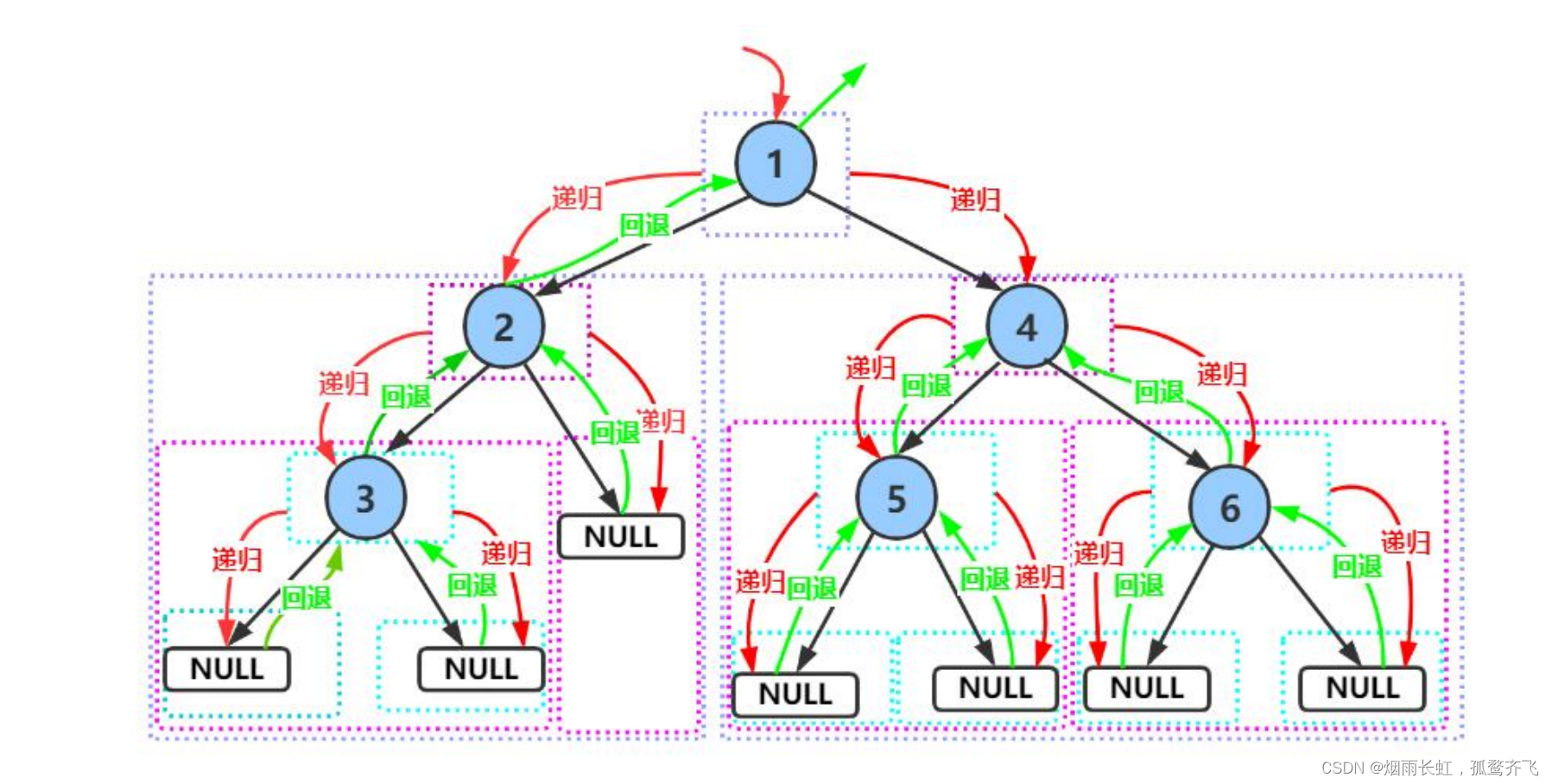
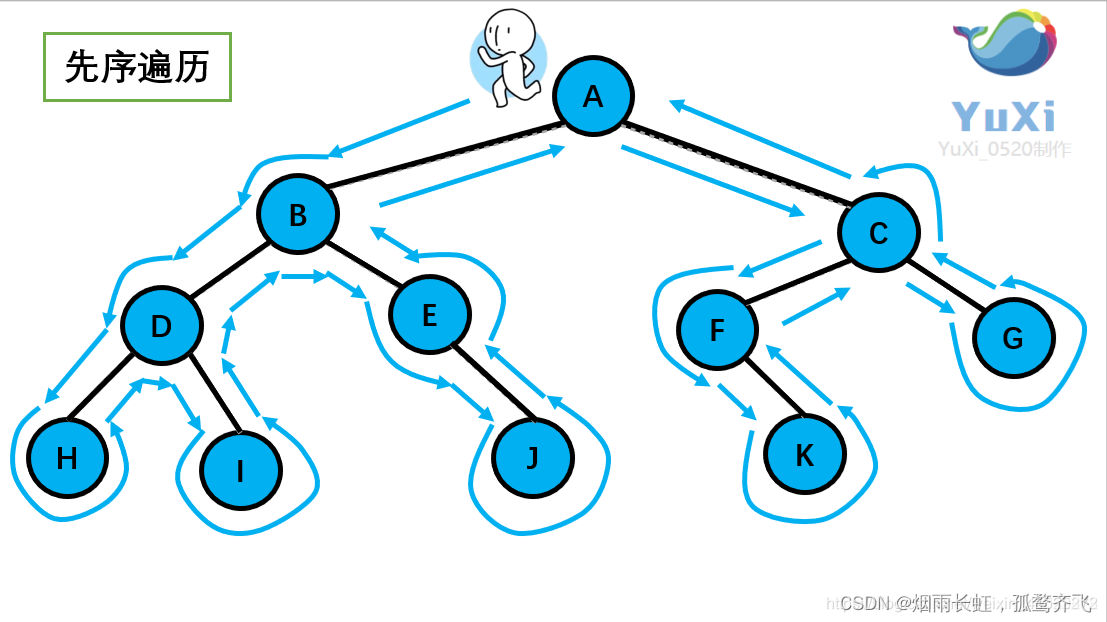
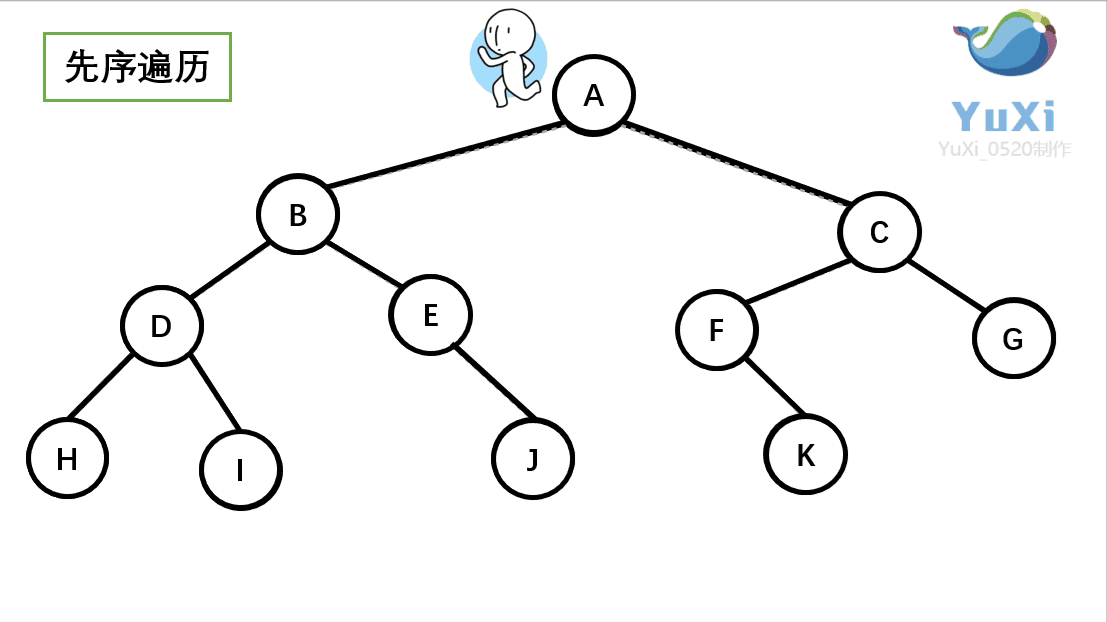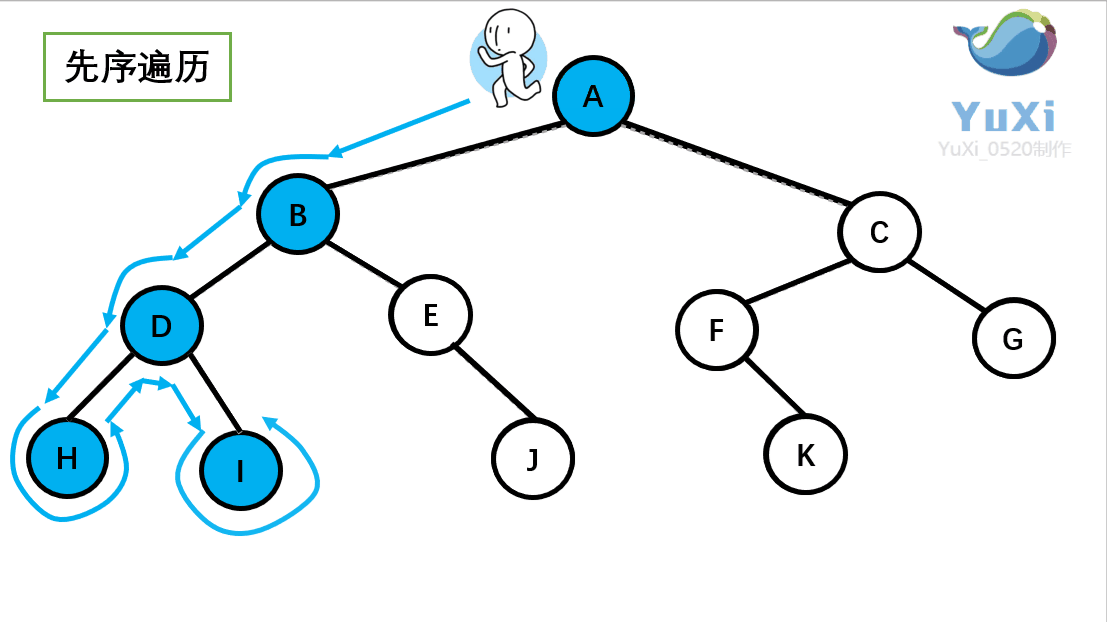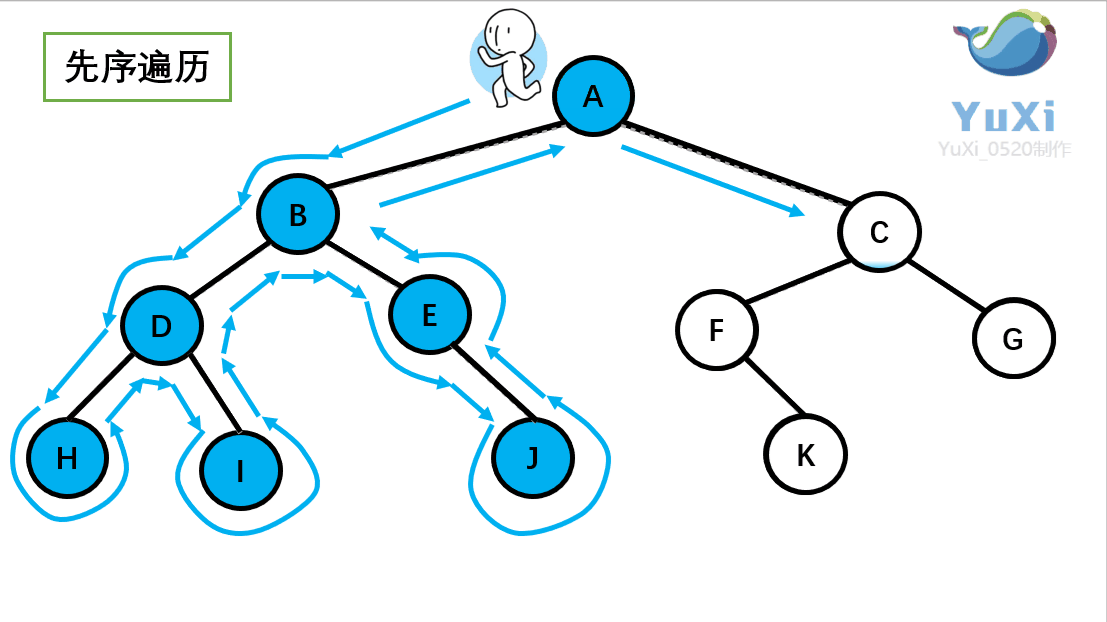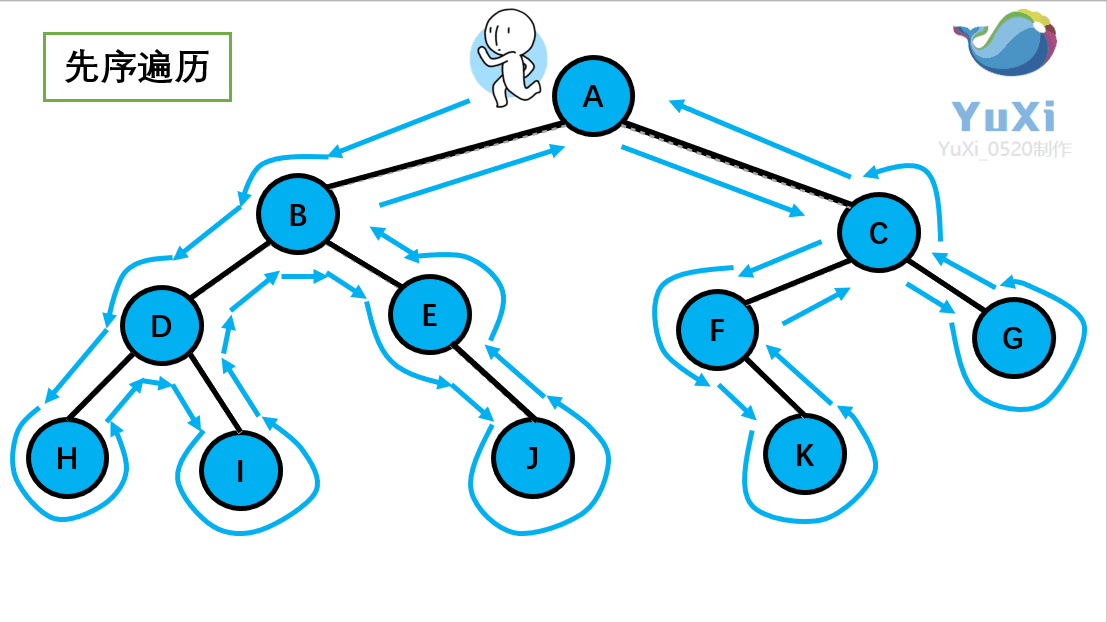
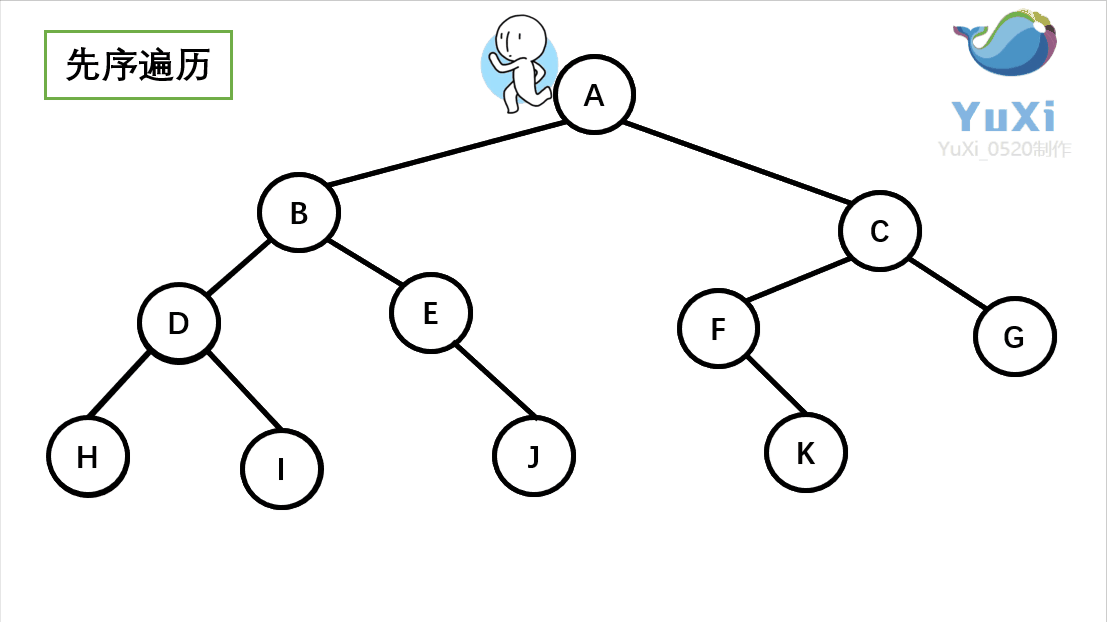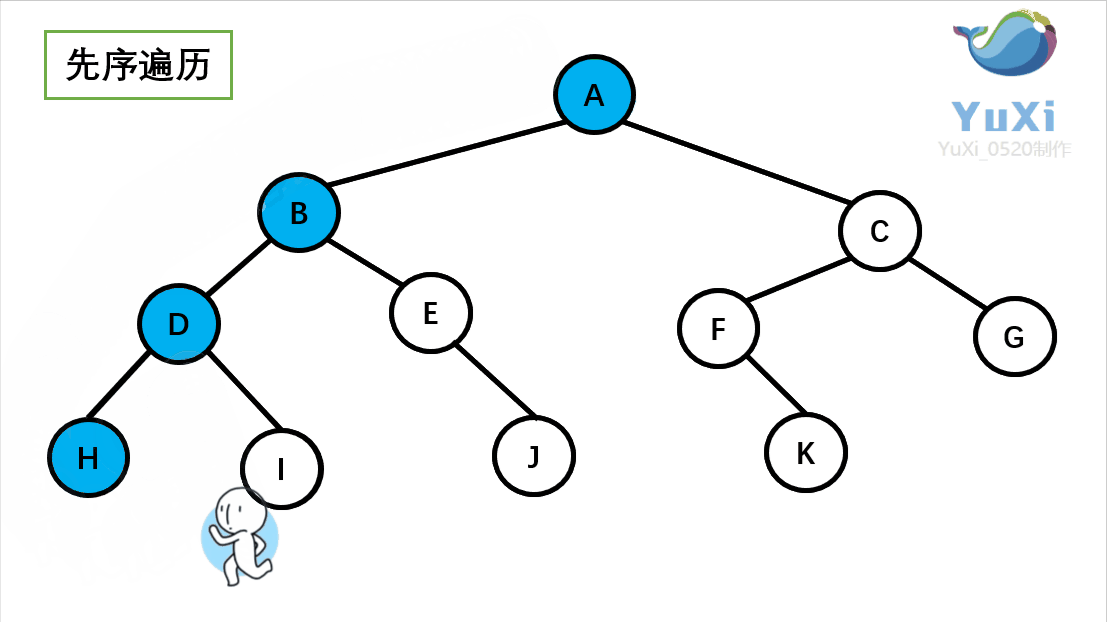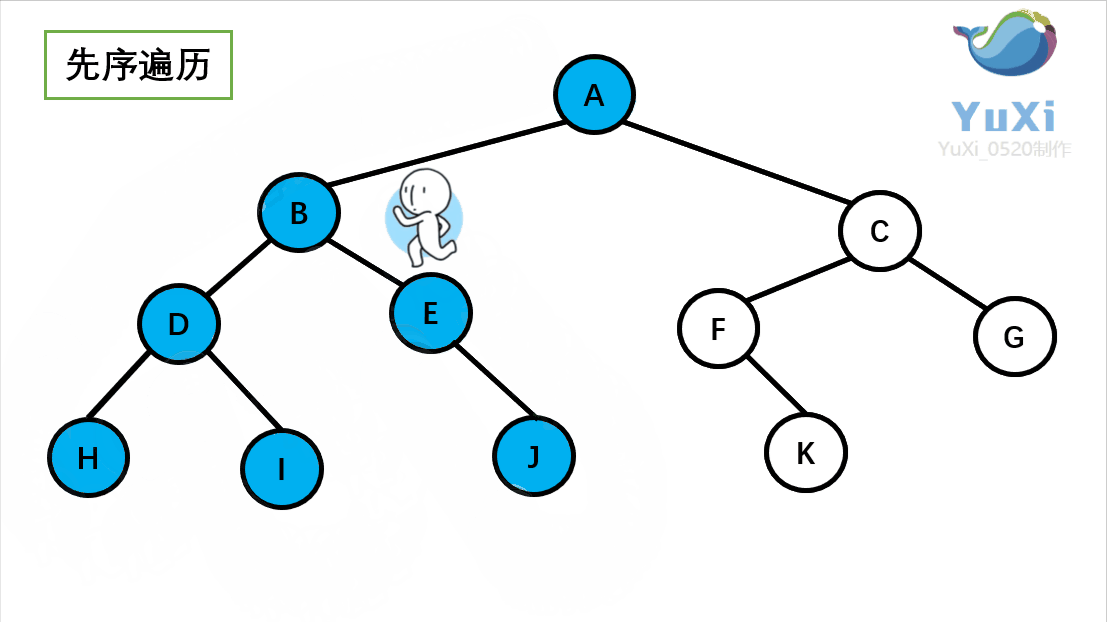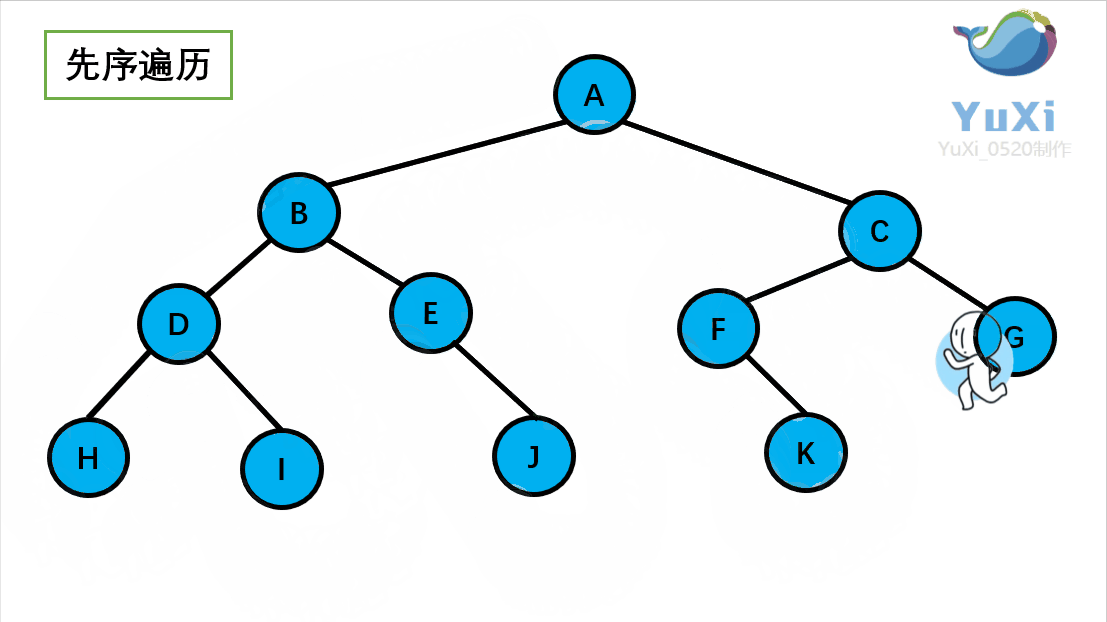
二叉树前序遍历
因为有些节点为空,我们可以选择打印和不打印,为了页面美观我们这里就不打印了
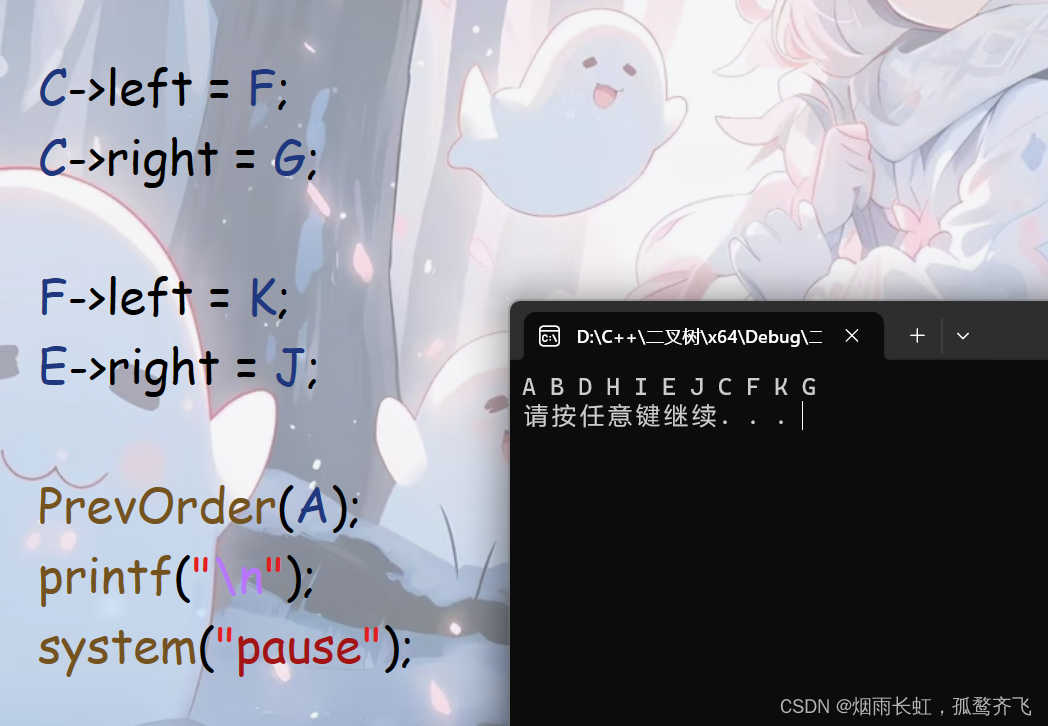
void PrevOrder(BTNode* root) {if (root == NULL){return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right); }int main() {BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;BTNode* F = (BTNode*)malloc(sizeof(BTNode));F->data = 'F';F->left = NULL;F->right = NULL;BTNode* G = (BTNode*)malloc(sizeof(BTNode));G->data = 'G';G->left = NULL;G->right = NULL;BTNode* H = (BTNode*)malloc(sizeof(BTNode));H->data = 'H';H->left = NULL;H->right = NULL;BTNode* I = (BTNode*)malloc(sizeof(BTNode));I->data = 'I';I->left = NULL;I->right = NULL;BTNode* J = (BTNode*)malloc(sizeof(BTNode));J->data = 'J';J->left = NULL;J->right = NULL;BTNode* K = (BTNode*)malloc(sizeof(BTNode));K->data = 'K';K->left = NULL;K->right = NULL;A->left = B;A->right = C;B->left = D;B->right = E;D->left = H;D->right = I;C->left = F;C->right = G;F->left = K;E->right = J;PrevOrder(A);printf("\n");system("pause");return 0; }以上我们插入树节点数据
代码测试
前序遍历结果:A B D H I E J C F K G
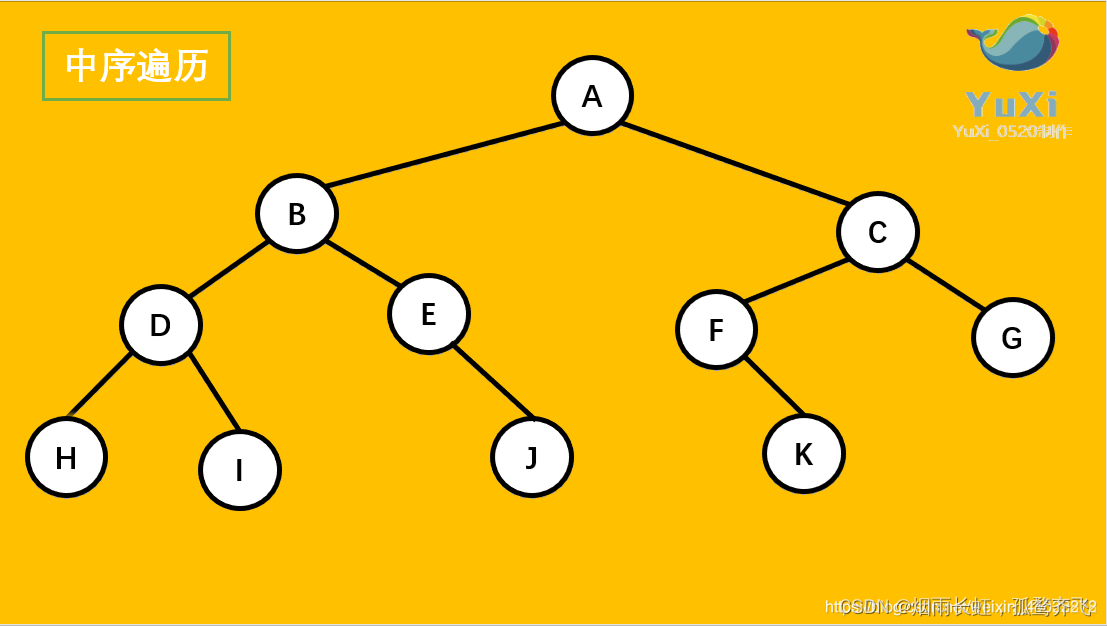
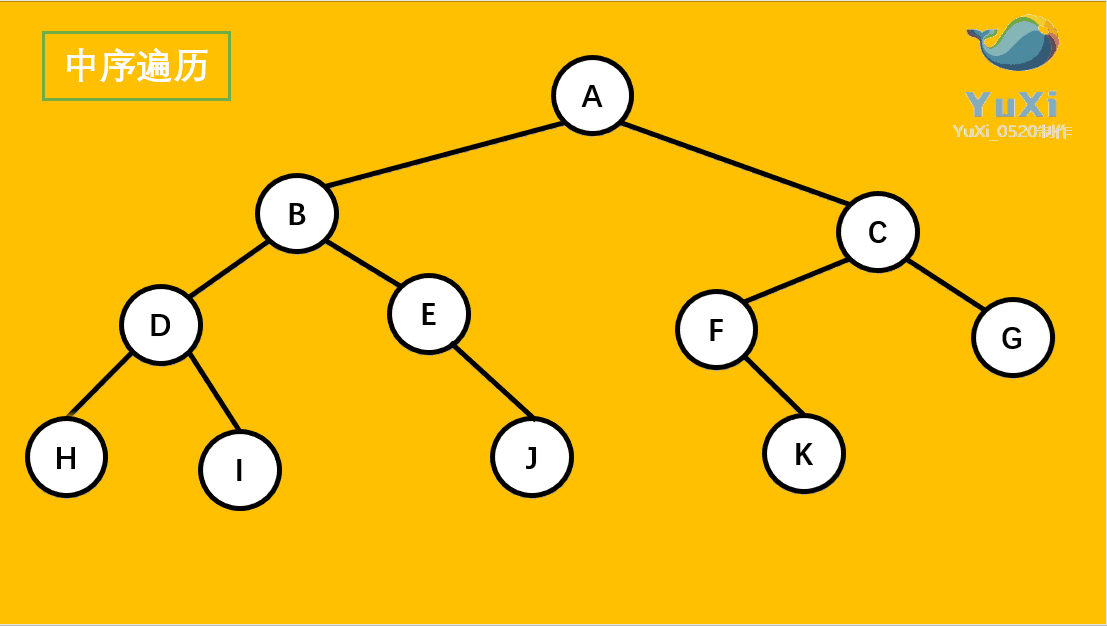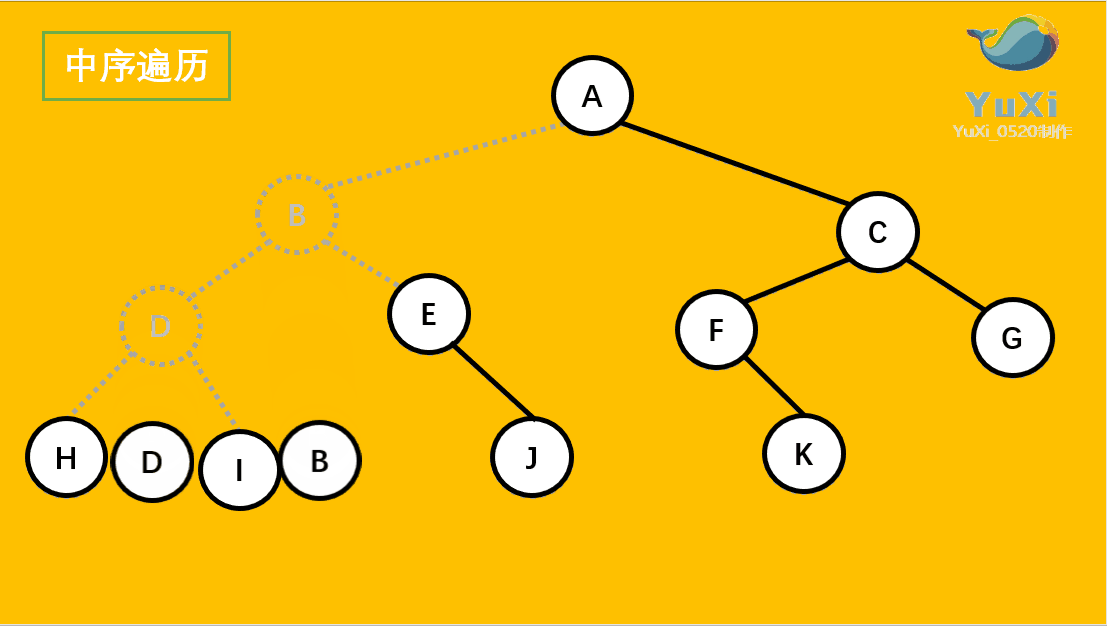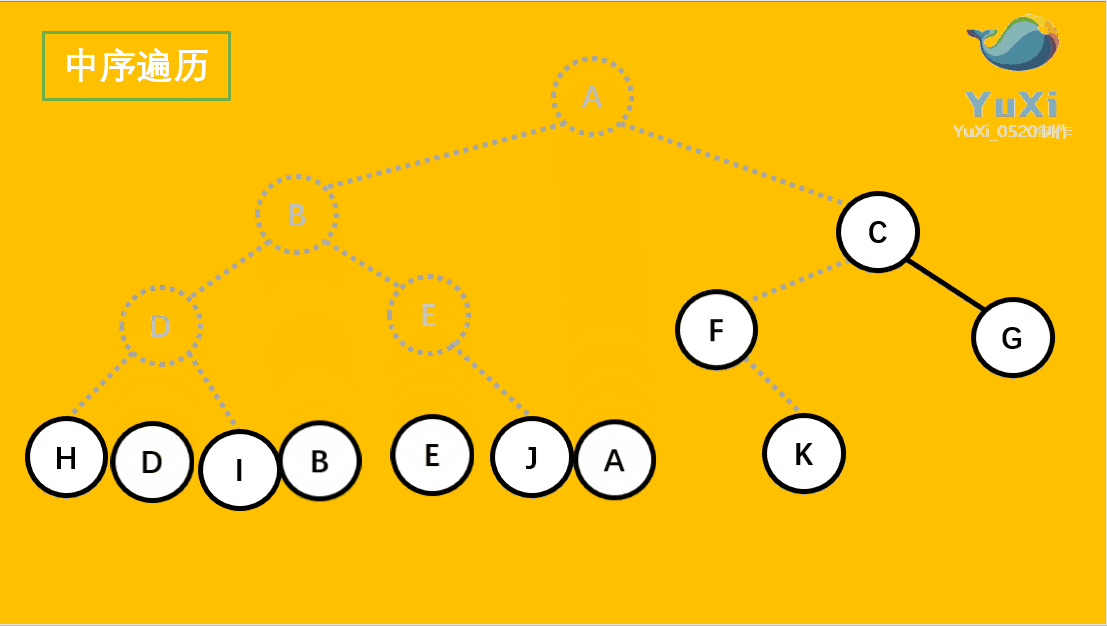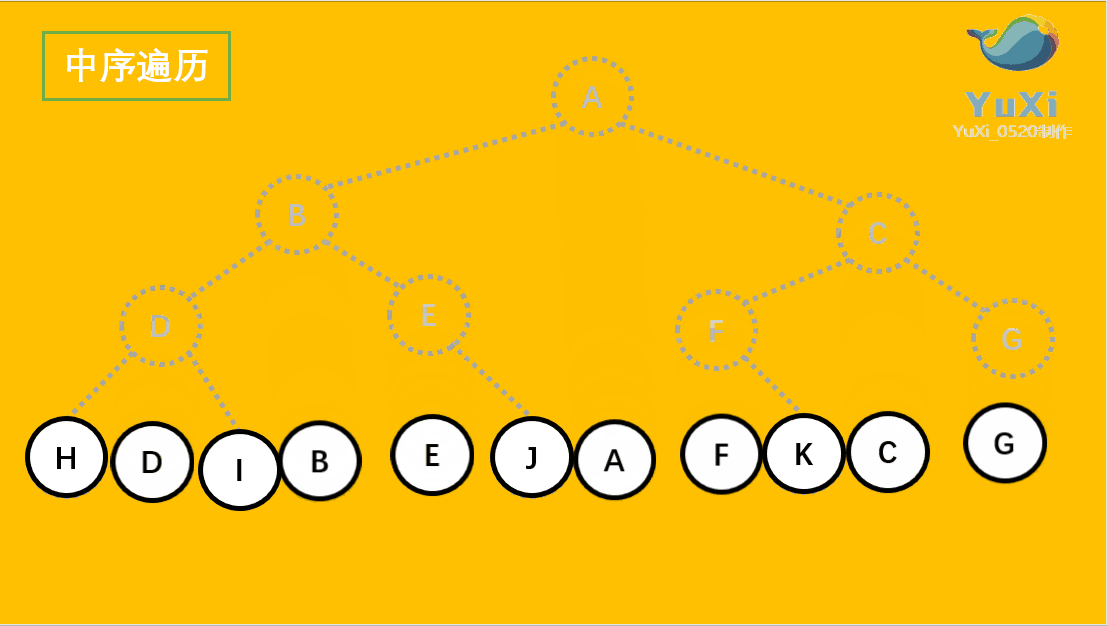
二叉树中序遍历
void InOrder(BTNode* root) {if (root == NULL){return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right); }代码测试
中序遍历结果:H D I B E J A F K C G
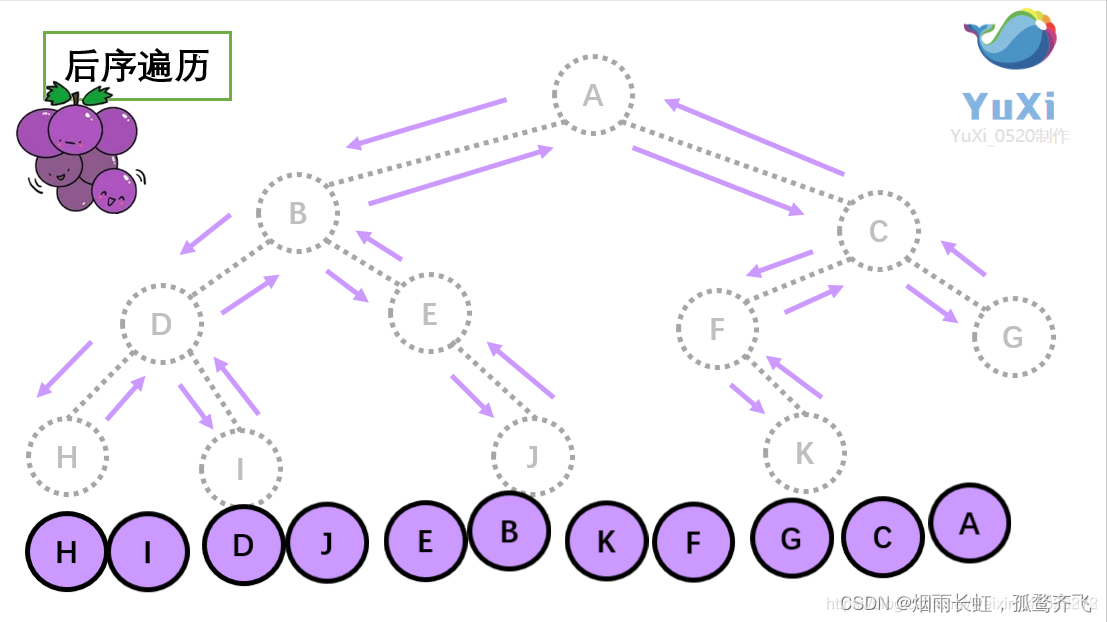
二叉树后序遍历
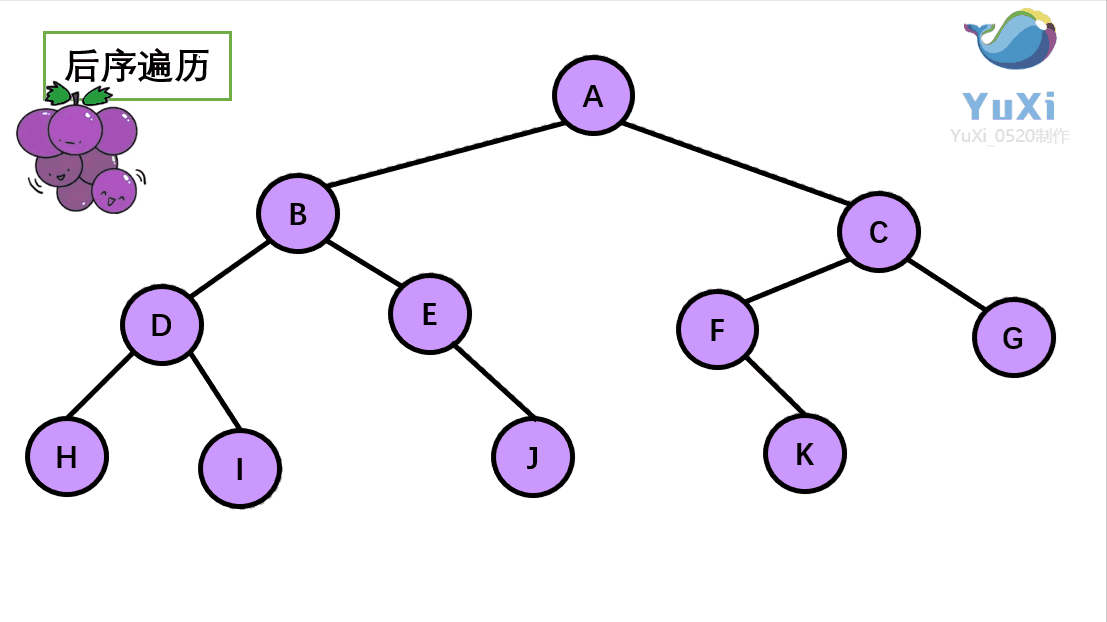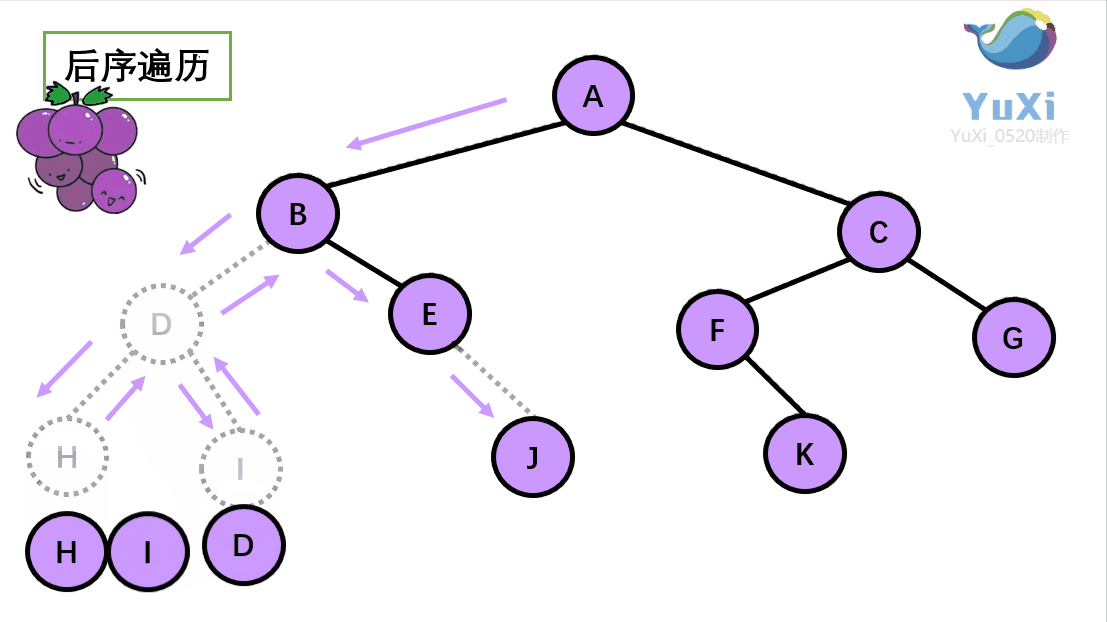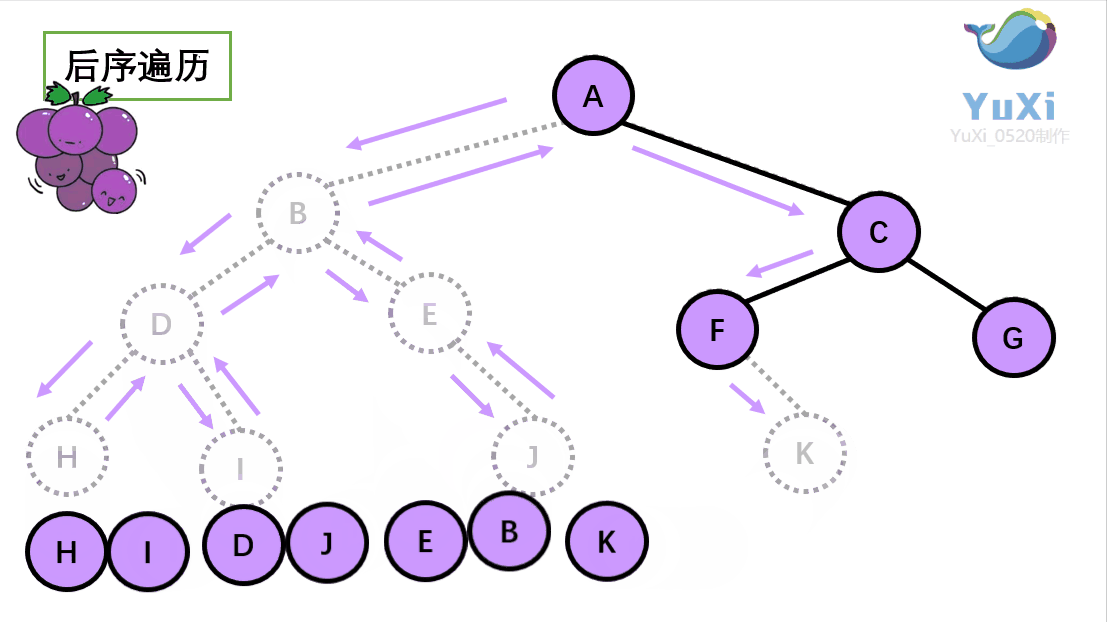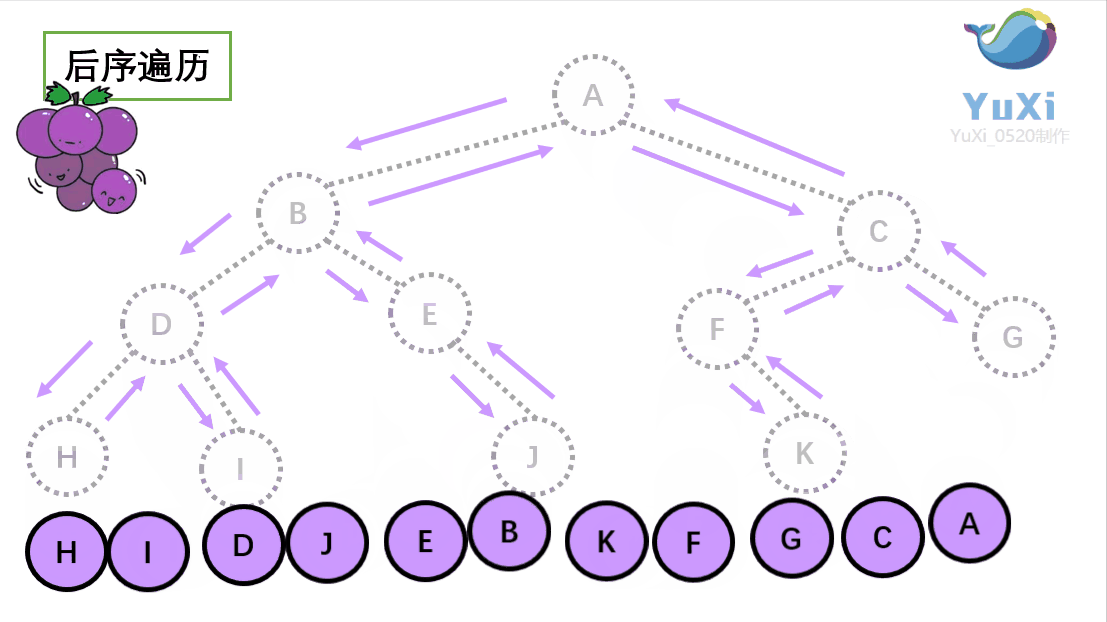
void PostOrder(BTNode* root) {if (root == NULL){return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data); }代码测试
后序遍历结果:H I D J E B K F G C A
二叉树遍历口诀
二叉树的层序遍历
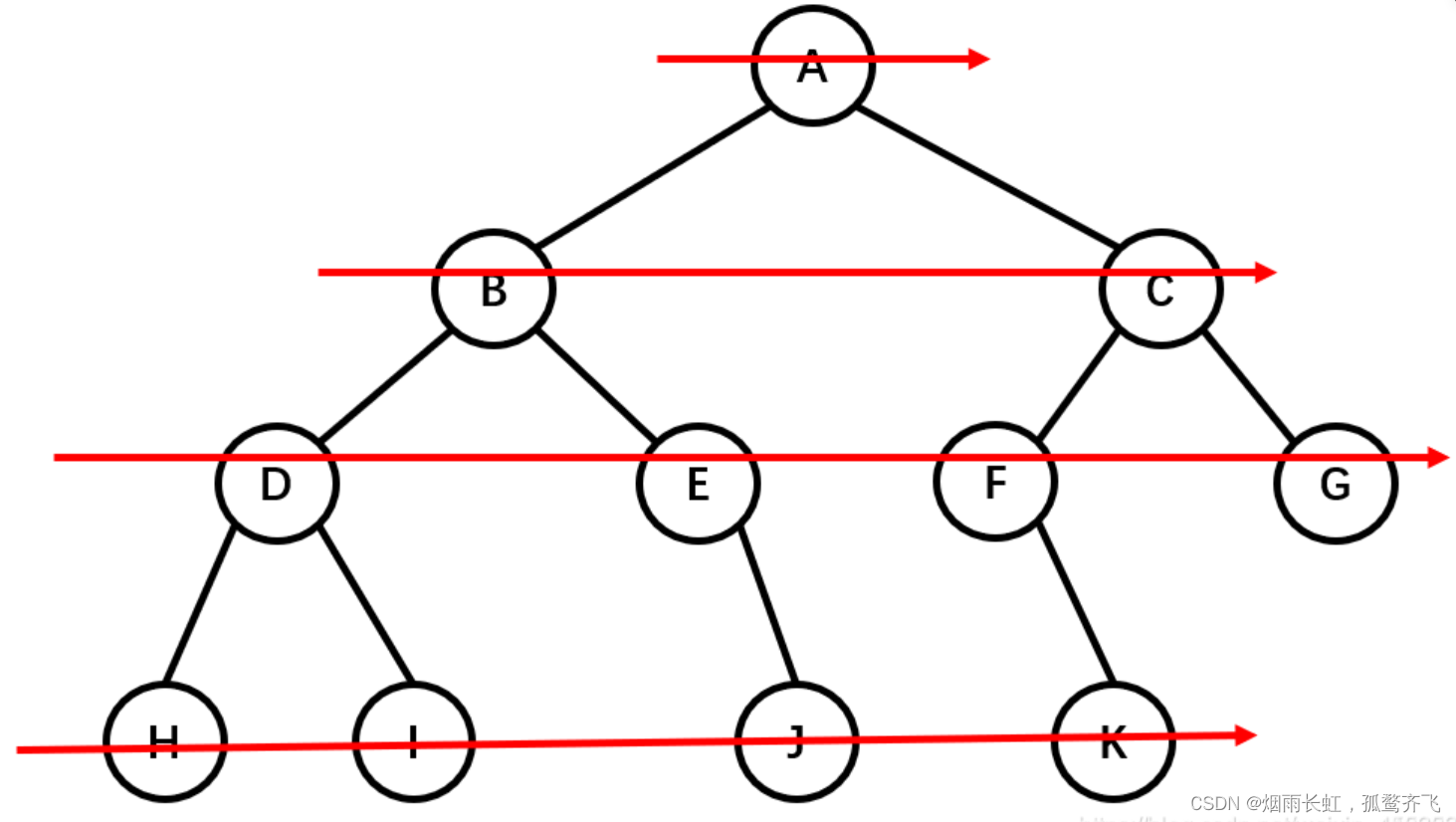
层序遍历太简单了,就是按照一层一层的顺序,从左到右写下来就行了
层序遍历结果:A B C D E F G H I J K
层序遍历我们要用到队列,所以我们这里要包一下队列相关的文件
C语言数据结构之线性表-栈和队列篇
void Levelorder(BTNode* root) {Queue q;QueueInit(&q);//树为空,直接返回if (root == NULL){return;}QueuePush(&q, root); //先将根节点入队while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); //出队保存队头并访问QueuePop(&q);printf("%c ", front->data);if (front->left) //将出队结点的左子树根入队{QueuePush(&q, front->left);}if (front->right) //将出队结点的右子树根入队{QueuePush(&q, front->right);}}printf("\n");QueueDestory(&q); //销毁队列 }
二叉树结点的个数
结点的个数的算法:左子树的结点加上右子树的结点,最后再加上根结点
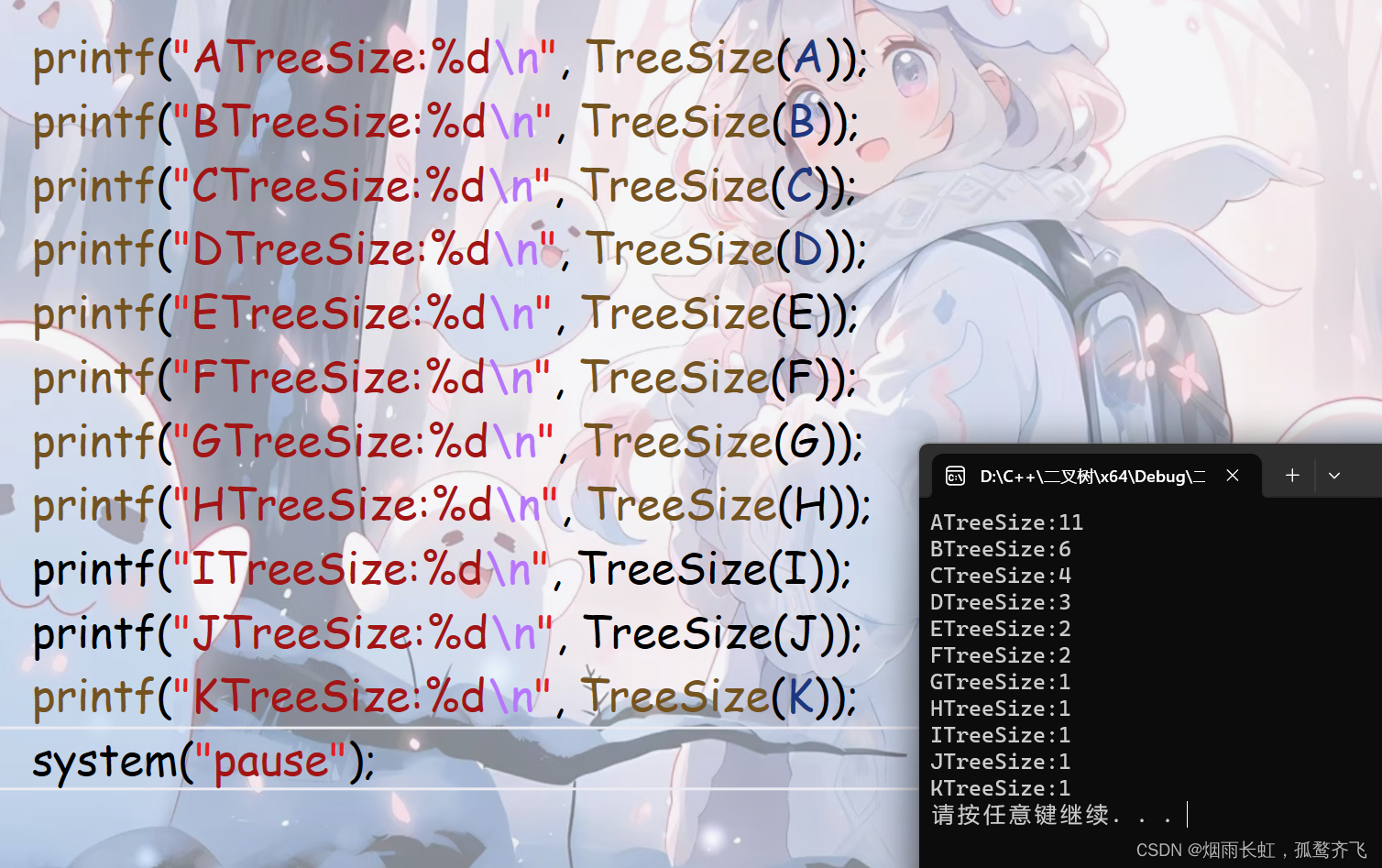
int TreeSize(BTNode* root) {return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1; }代码测试
二叉树叶子结点的个数
叶子结点的特征:左右子树为空,我们可以通过递归的方法遍历每一颗子树
int TreeLeafSizee(BTNode* root) {if (root == NULL)return 0;//左右为空if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSizee(root->left) + TreeLeafSizee(root->right); }我们还是以这个树为例
我们发现有H、I、J、K、G五个左右子树为空,所以叶子结点的个数为5
代码测试
二叉树的高度
树的高度的定义:从 根开始定义 起,根为第一层,根的孩子为第二层,以此类推
int TreeHeight(BTNode* root) {if (root == NULL)return 0;int left = TreeHeight(root->left);int right = TreeHeight(root->right);return (left > right ? left : right) + 1; }代码测试
二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k) {if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1); }代码测试
如图所示:4层的结点为4,2层的节点为2
二叉树查找值为x的节点
先对左子树递归查找,如果未找到x,则返回NULL
如果找到x,便返回x所在节点
根据返回值判断是否需要进行右递归查找操作
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {if (root == NULL)return NULL;if (root->data == x)return root;if (BinaryTreeFind(root->left, x))return BinaryTreeFind(root->left, x);elsereturn BinaryTreeFind(root->right, x); }
总结:
二叉树主要涉及的算法有 递归 和 分治
递归需要画图理解其真谛
相关文章:
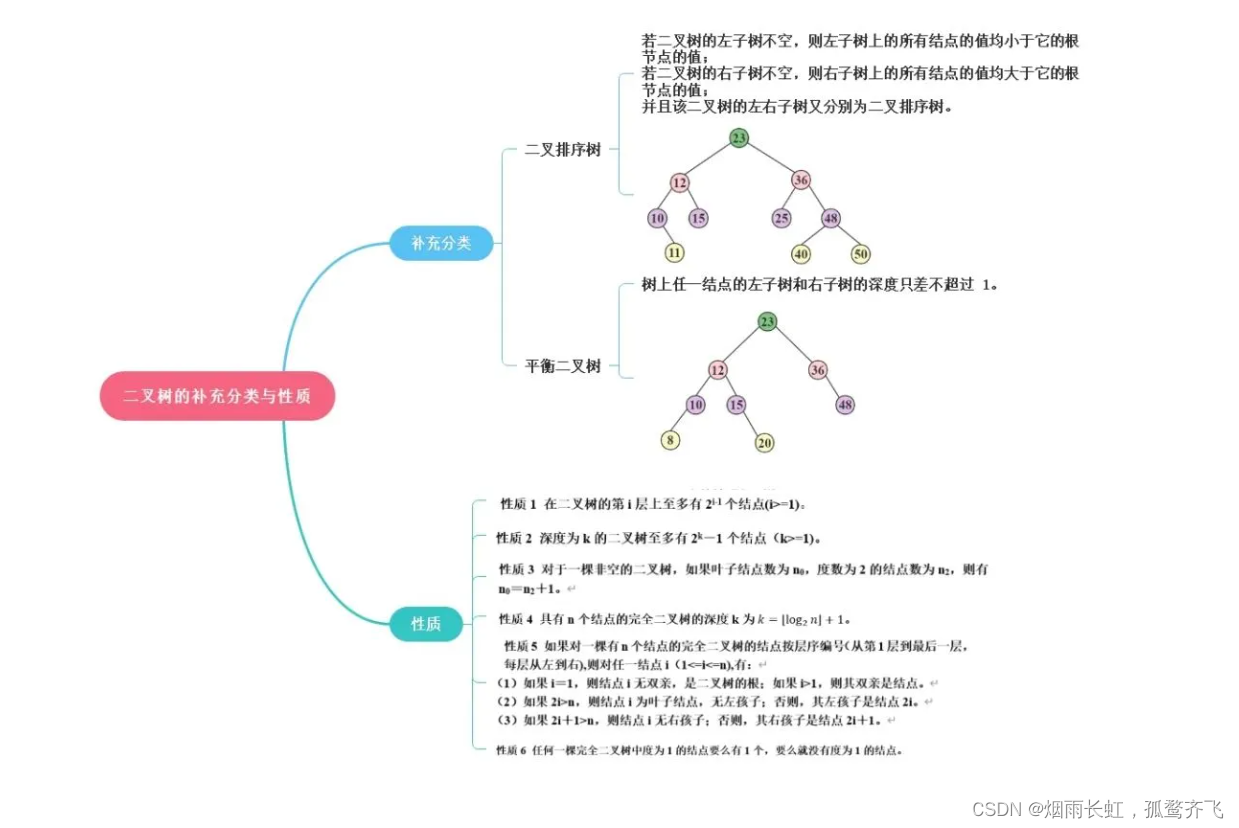
C语言数据结构之二叉树
少年恃险若平地 独倚长剑凌清秋 🎥烟雨长虹,孤鹜齐飞的个人主页 🔥个人专栏 🎥前期回顾-栈和队列 期待小伙伴们的支持与关注!!! 目录 树的定义与判定 树的定义 树的判定 树的相关概念 树的运用…...

《HTML 简易速速上手小册》第1章:HTML 入门(2024 最新版)
文章目录 1.1 HTML 简介与历史(😉🌐👽踏上神奇的网页编程之旅)1.1.1 从过去到现在的华丽蜕变1.1.2 市场需求 —— HTML的黄金时代1.1.3 企业中的实际应用 —— 不只是个网页1.1.4 职业前景 —— 未来属于你 1.2 基本 H…...
笔记本电脑Win11重装系统教程
在笔记本电脑Win11操作过程中,用户如果遇到很严重的系统问题,就可以重新正常的Win11系统,快速解决Win11系统问题。但是,部分新手用户不知道不知道如何操作才能给Win11笔记本电脑重装系统?以下小编分享笔记本电脑Win11重…...
))
突破编程_C++_面试(基础知识(3))
面试题5:函数调用的过程 C 中函数的调用包含参数入栈、函数跳转、保护现场、回复现场等过程,重点过程如下: (1)将函数的参数压入栈中,从右至左压入。 (2)调用函数时,将当…...
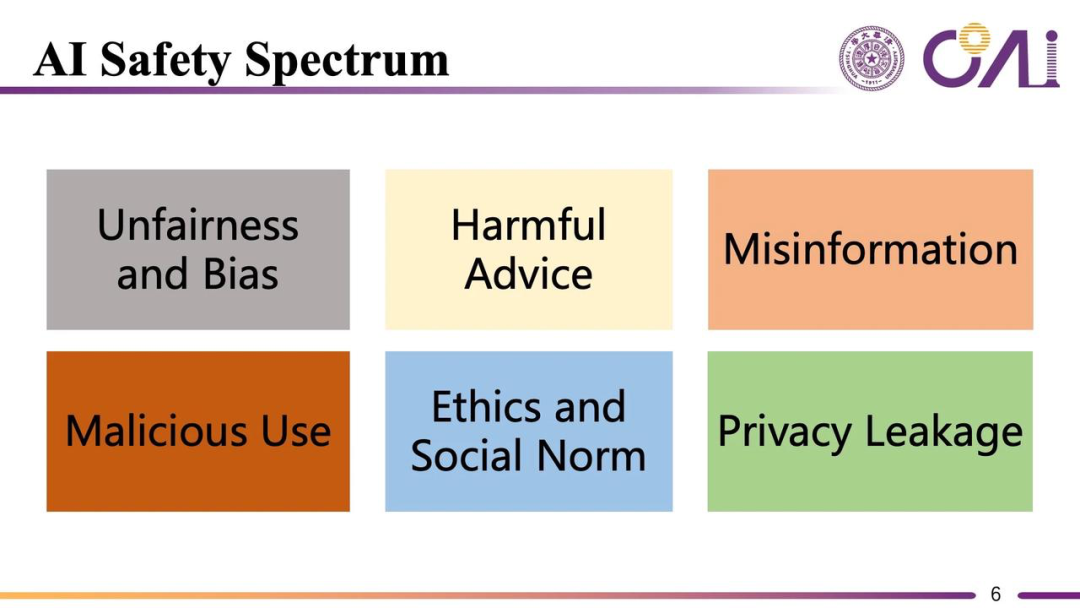
AI的安全应答之道
作者:统信UOS技术团队 2023,随着各种大语言模型的爆发,整个AI生态正处于从决策式AI进化到生成式AI的进程中。各类AI模型和AI应用层出不穷,也随之带来了与AI相关的各类潜在风险。AI开发和使用过程中的风险防范和治理,成为了不可忽…...

【昕宝爸爸小模块】日志系列之什么是分布式日志系统
➡️博客首页 https://blog.csdn.net/Java_Yangxiaoyuan 欢迎优秀的你👍点赞、🗂️收藏、加❤️关注哦。 本文章CSDN首发,欢迎转载,要注明出处哦! 先感谢优秀的你能认真的看完本文&…...
如何在淘宝和Shopee上进行选品:策略和原则
在当今数字化时代,电商平台已经成为卖家们扩展业务和增加销售额的重要渠道。而在淘宝和Shopee这两个知名电商平台上进行选品时,卖家可以遵循一些相似的原则和策略,以确保他们的产品能够吸引目标客户并取得成功。本文将为您介绍一些在淘宝和Sh…...
C++/数据结构:二叉搜索树的实现与应用
目录 一、二叉搜索树简介 二、二叉搜索树的结构与实现 2.1二叉树的查找与插入 2.2二叉树的删除 2.3二叉搜索树的实现 2.3.1非递归实现 2.3.2递归实现 三、二叉搜索树的k模型和kv模型 一、二叉搜索树简介 二叉搜索树又称二叉排序树,它或者是一棵空树࿰…...
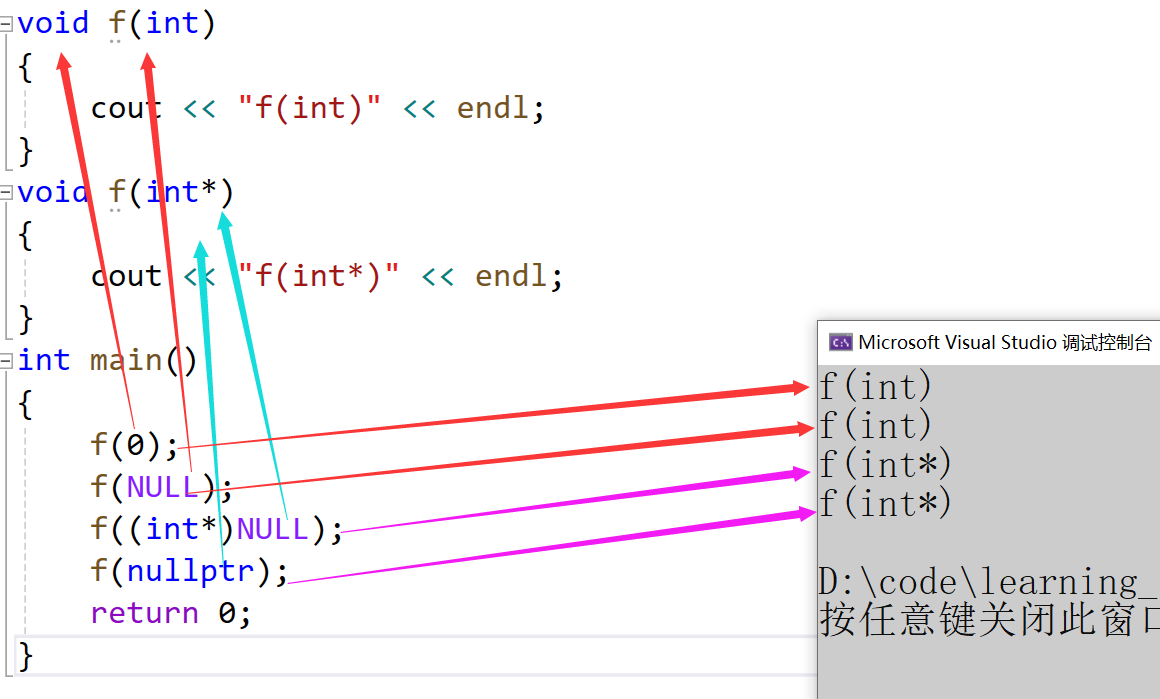
C++引用、内联函数、auto关键字介绍以及C++中无法使用NULL的原因
文章目录 一、引用1.1 引用概念1.2 引用特性1.3 常引用1.4 使用场景1.4.1 做参数1.4.2做返回值 1.5 引用和指针的区别1.6 小结一下 二、内联函数2.1 内联的概念2.2 内联的特性2.3 【面试题】 三、auto关键字(C11)3.1 类型别名思考3.2 auto简介 四、auto的使用细则4.1 基于范围的…...
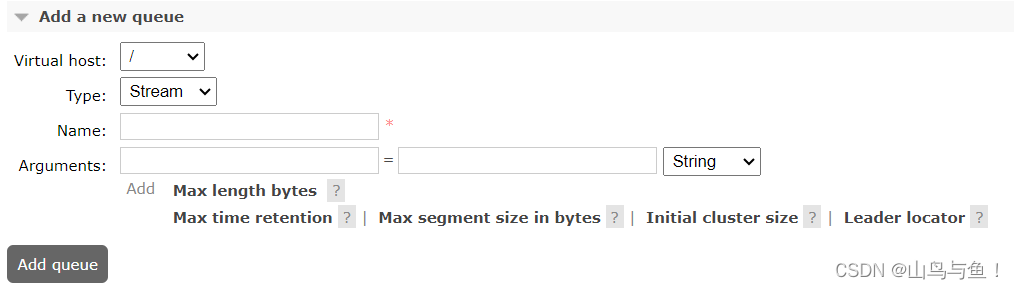
RabbitMQ之三种队列之间的区别及如何选型
目录 不同队列之间的区别 Classic经典队列 Quorum仲裁队列 Stream流式队列 如何使用不同类型的队列 Quorum队列 Stream队列 不同队列之间的区别 Classic经典队列 这是RabbitMQ最为经典的队列类型。在单机环境中,拥有比较高的消息可靠性。 经典队列可以选…...

【ArcGIS微课1000例】0099:土地利用变化分析
本实验讲述在ArcGIS软件中基于两期土地利用数据,做土地利用变化分析。 文章目录 一、实验描述二、实验过程三、注意事项一、实验描述 对城市土地利用情况进行分析时,需要考虑不同时期土地利用图层在空间上的差异性,如农用地转建筑用地的空间变化。而该变化过程表现为各时期…...
学习鸿蒙基础(2)
arkts是声名式UI DevEcoStudio的右侧预览器可以预览。有个TT的图标可以看布局的大小。和html的布局浏览很像。 上图布局对应的代码: Entry //入口 Component struct Index {State message: string Hello Harmonyos //State 数据改变了也刷新的标签build() {Row()…...

2024年美国大学生数学建模竞赛思路与源代码【2024美赛C题】
B站账号,提前关注,会有直播:有为社的个人空间-有为社个人主页-哔哩哔哩视频 (bilibili.com) 题目 待定 问题一 思路 待定 模型 待定 程序 待定 问题二 待定 思路 待定 模型 待定 程序 待定...
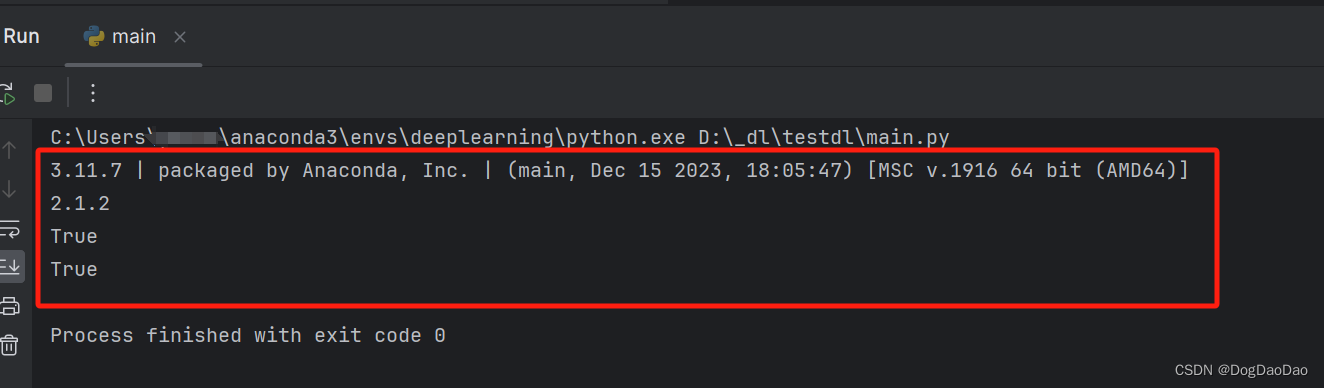
Windows11搭建GPU版本PyTorch环境详细过程
Anaconda安装 https://www.anaconda.com/ Anaconda: 中文大蟒蛇,是一个开源的Python发行版本,其包含了conda、Python等180多个科学包及其依赖项。从官网下载Setup:点击安装,之后勾选上可以方便在普通命令行cmd和PowerShell中使用…...

Springboot项目基础配置:小白也能快速上手!
推荐文章 给软件行业带来了春天——揭秘Spring究竟是何方神圣(一) 给软件行业带来了春天——揭秘Spring究竟是何方神圣(二) 给软件行业带来了春天——揭秘Spring究竟是何方神圣(三) 给软件行业带来了春天—…...
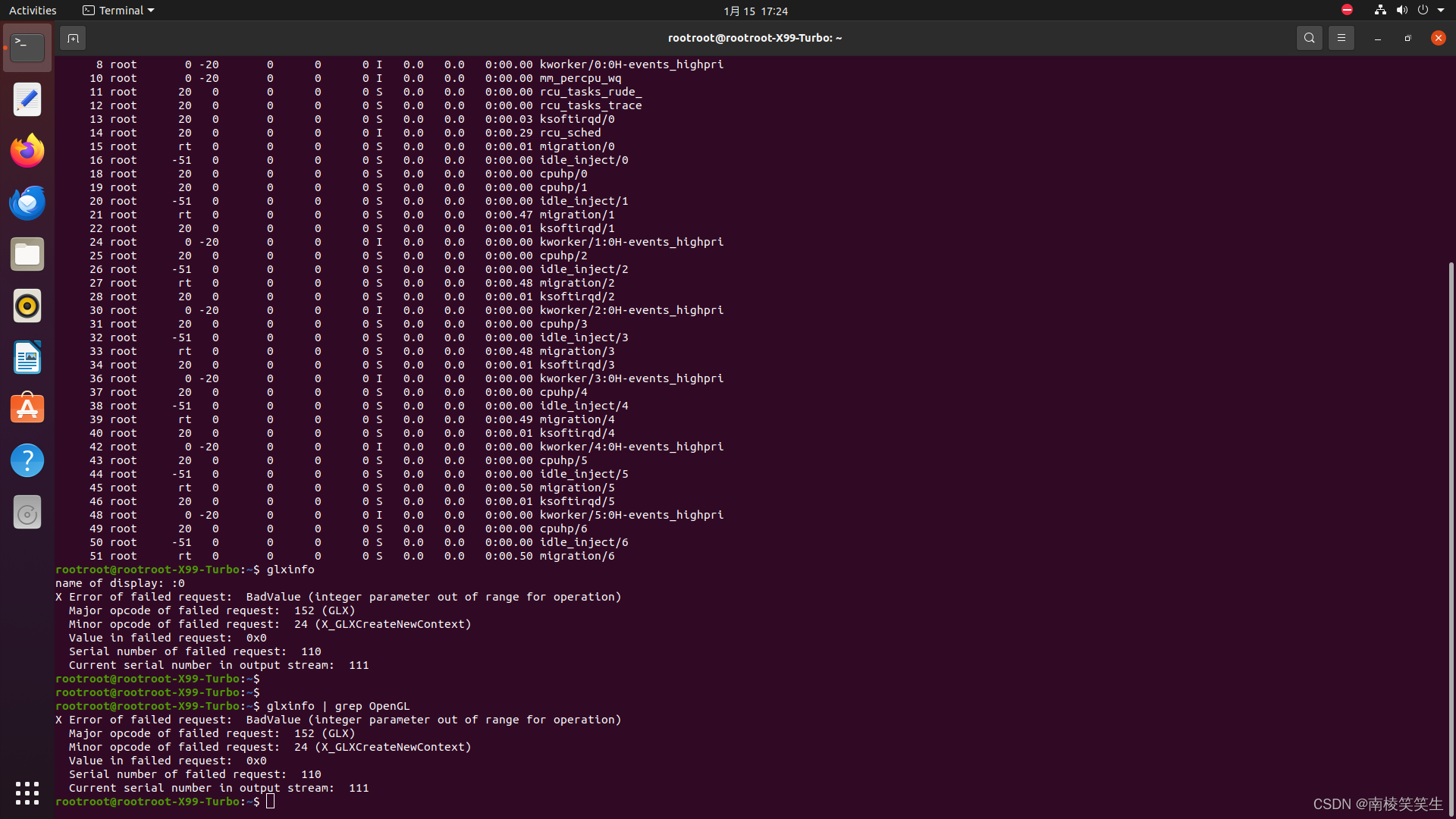
20240127在ubuntu20.04.6下配置whisper
20240131在ubuntu20.04.6下配置whisper 2024/1/31 15:48 首先你要有一张NVIDIA的显卡,比如我用的PDD拼多多的二手GTX1080显卡。【并且极其可能是矿卡!】800¥ 2、请正确安装好NVIDIA最新的驱动程序和CUDA。可选安装! 3、配置whispe…...

C# 递归执行顺序
为了方便进一步理解递归,写了一个数字输出 class Program {static void Main(string[] args){int number 5;RecursiveDecrease(number);}static void RecursiveDecrease(int n){if (n > 0){Console.WriteLine("Before recursive call do : " n);Rec…...
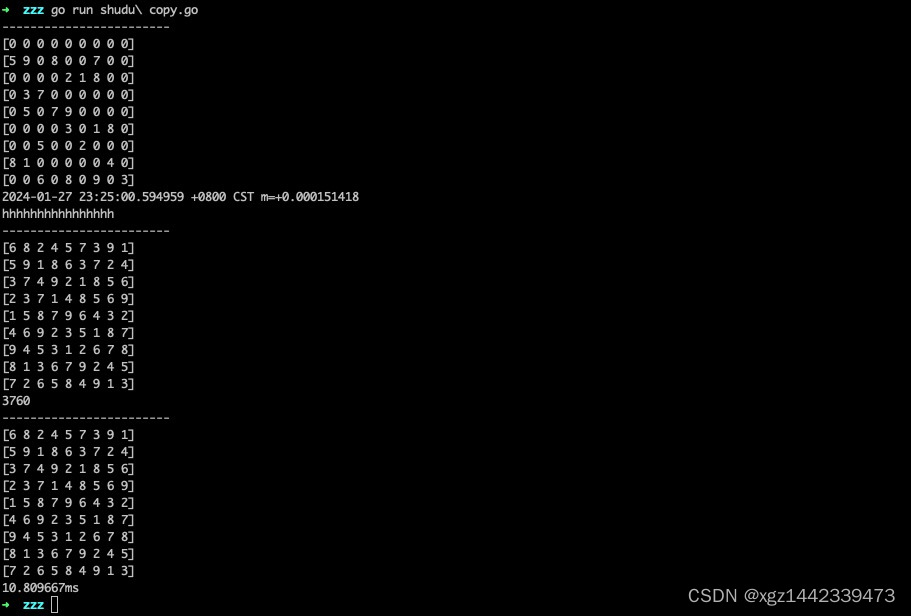
go 实现暴力破解数独
一切罪恶的来源是昨晚睡前玩了一把数独,找虐的选了个最难的模式,做了一个多小时才做完,然后就睡不着了..........程序员不能受这委屈,今天咋样也得把这玩意儿破解了 破解思路(暴力破解加深度遍历) 把数独…...

go语言-字符串处理常用函数
本文介绍go语言处理字符串类型的常见函数。 ## 多行字符串 在 Go 中创建多行字符串非常容易。只需要在你声明或赋值时使用 () 。 str : This is a multiline string. ## 字符串的拼接 go // fmt.Sprintf方式拼接字符串 str1 : "abc" str2 : "def" …...
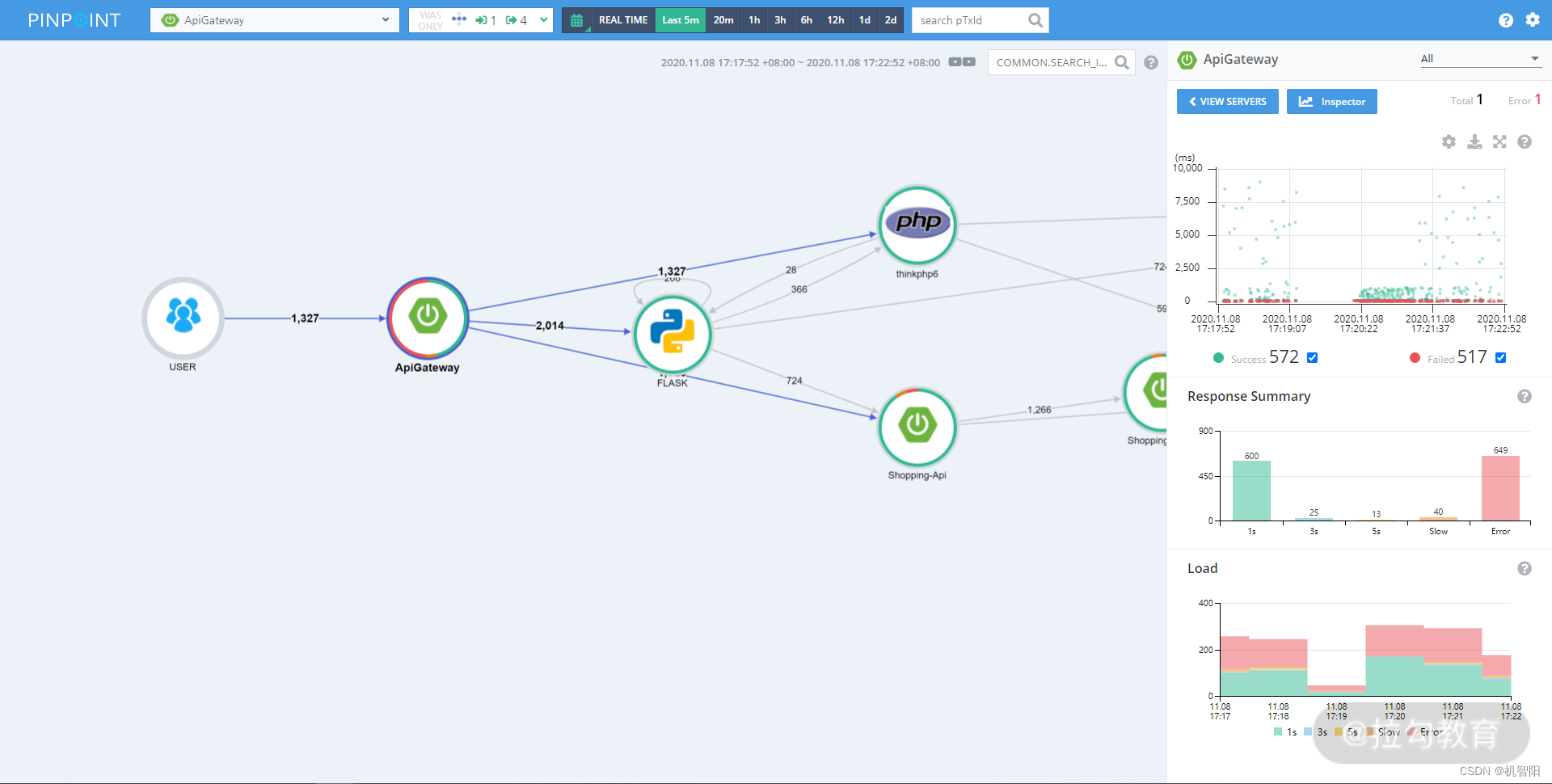
DevOps落地笔记-05|非功能需求:如何有效关注非功能需求
上一讲主要介绍了看板方法以及如何使用看板方法来解决软件研发过程中出现的团队过载、工作不均、任务延期等问题。通过学习前面几个课时介绍的知识,你的团队开始源源不断地交付用户价值。用户对交付的功能非常满意,但等到系统上线后经常出现服务不可用的…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...