深度强化学习(王树森)笔记11
深度强化学习(DRL)
本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。
参考链接
Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL
源代码链接:https://github.com/DeepRLChinese/DeepRL-Chinese
B站视频:【王树森】深度强化学习(DRL)
豆瓣: 深度强化学习
文章目录
- 深度强化学习(DRL)
- 策略学习高级技巧
- Trust Region Policy Optimization (TRPO)
- 置信域方法
- 策略学习
- TRPO 数学推导
- 训练流程
- 后记
策略学习的高级技巧:置信域策略优化 (TRPO)
PPO算法就是在TRPO的基础上推出的。
策略学习高级技巧
本章介绍策略学习的高级技巧。介绍置信域策略优化 (TRPO), 它是一种策略学习方法,可以代替策略梯度方法。
Trust Region Policy Optimization (TRPO)
置信域策略优化 (trust region policy optimization, TRPO) 是一种策略学习方法,跟以前学的策略梯度有很多相似之处。跟策略梯度方法相比,TRPO 有两个优势:第一,TRPO 表现更稳定,收敛曲线不会剧烈波动,而且对学习率不敏感;第二,TRPO 用更少的经验(即智能体收集到的状态、动作、奖励) 就能达到与策略梯度方法相同的表现。
学习TRPO 的关键在于理解置信域方法(trustregion methods)。置信域方法不是TRPO 的论文提出的,而是数值最优化领域中一类经典的算法,历史至少可以追溯到 1970 年。TRPO 论文的贡献在于巧妙地把置信域方法应用到强化学习中,取得非常好的效果。
置信域方法
有这样一个优化问题: max θ J ( θ ) \max_{\boldsymbol{\theta}}J(\boldsymbol{\theta}) maxθJ(θ)。这里的 J ( θ ) J(\boldsymbol{\theta}) J(θ) 是目标函数, θ \theta θ 是优化变量。求解这个优化问题的目的是找到一个变量 θ \theta θ 使得目标函数 J ( θ ) J(\theta) J(θ) 取得最大值。有各种各样的优化算法用于解决这个问题。几乎所有的数值优化算法都是做这样的迭代:
θ n e w ← U p d a t e ( Data; θ n o w ) . \begin{array}{rcl}\theta_\mathrm{new}&\leftarrow&\mathrm{Update}\left(\text{Data; }\theta_\mathrm{now}\right).\end{array} θnew←Update(Data; θnow).
此处的 θ n o w \theta_\mathrm{now} θnow 和 θ n e w \theta_\mathrm{new} θnew 分别是优化变量当前的值和新的值。不同算法的区别在于具体怎么样利用数据更新优化变量。
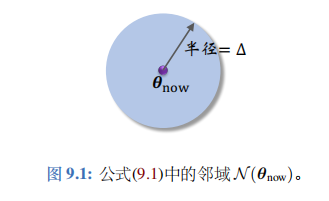
置信域方法用到一个概念——置信域。下面介绍置信域。给定变量当前的值 θ n o w \theta_\mathrm{now} θnow,用 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 表示 θ n o w \theta_\mathrm{now} θnow 的一个邻域。举个例子:
N ( θ n o w ) = { θ ∣ ∥ θ − θ n o w ∥ 2 ≤ Δ } . ( 9.1 ) \mathcal{N}(\theta_{\mathrm{now}})\:=\:\Big\{\theta\:\Big|\:\left\|\theta-\theta_{\mathrm{now}}\right\|_{2}\leq\Delta\Big\}.\quad(9.1) N(θnow)={θ ∥θ−θnow∥2≤Δ}.(9.1)
这个例子中,集合 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 是以 θ n o w \theta_\mathrm{now} θnow 为球心、 以 Δ \Delta Δ为半径的球;见右图。球中的点都足够接近 θ n o w \theta_\mathrm{now} θnow。
置信域方法需要构造一个函数 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow),这个函数要满足这个条件:
L ( θ ∣ θ n o w ) 很接近 J ( θ ) , ∀ θ ∈ N ( θ n o w ) , L(\boldsymbol{\theta}\mid\boldsymbol{\theta_\mathrm{now}})\text{ 很接近 }J(\boldsymbol{\theta}),\quad\forall\boldsymbol{\theta}\in\mathcal{N}(\boldsymbol{\theta_\mathrm{now}}), L(θ∣θnow) 很接近 J(θ),∀θ∈N(θnow),
那么集合 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow)就被称作置信域。顾名思义,在 θ n o w \theta_\mathrm{now} θnow的邻域上,我们可以信任 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow), 可以拿 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 来替代目标函数 J ( θ ) J(\theta) J(θ) 。
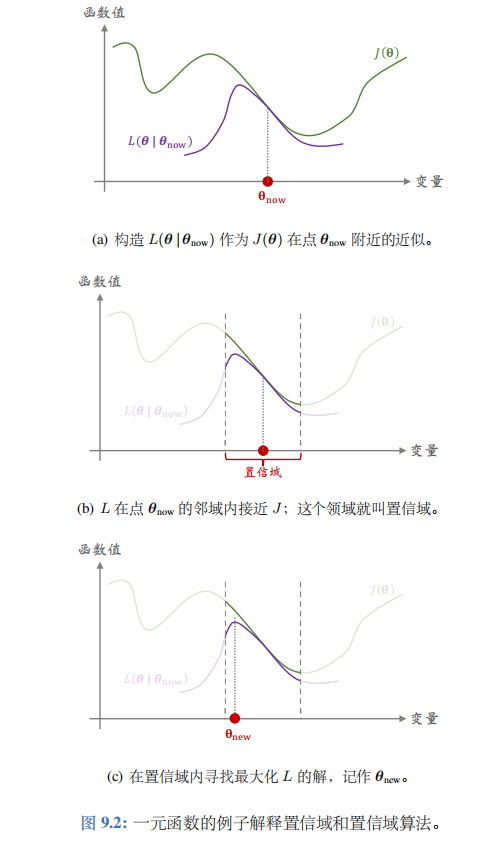
图 9.2 用一个一元函数的例子解释 J ( θ ) J(\theta) J(θ) 和 L ( θ ∣ θ n o w ) L(\theta\mid\theta_\mathrm{now}) L(θ∣θnow) 的关系。图中横轴是优化变量 θ \theta θ,纵轴是函数值。如图 9.2(a)所示,函数 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 未必在整个定义域上都接近 J ( θ ) J(\theta) J(θ),而只是在 θ n o w \theta_\mathrm{now} θnow的领域里接近 J ( θ ) J(\theta) J(θ)。 θ n o w \theta_\mathrm{now} θnow 的邻域就叫做置信域。
通常来说, J J J是个很复杂的函数,我们甚至可能不知道 J J J 的解析表达式(比如 J J J 是某个函数的期望)。而我们人为构造出的函数 L L L 相对较为简单,比如 L L L 是 J J J 的蒙特卡洛近似,或者是 J J J在 θ n o w \theta_\mathrm{now} θnow这个点的二阶泰勒展开。既然可以信任 L L L,那么不妨用 L L L 代替复杂的函数 J J J,然后对 L L L做最大化。这样比直接优化 J J J 要容易得多。这就是置信域方法的思想。
具体来说,置信域方法做下面这两个步骤,一直重复下去,当无法让 J J J 的值增大的时候终止算法。
第一步——做近似:给定 θ n o w \theta_\mathrm{now} θnow,构造函数 L ( θ ∣ θ n ε w ) L(\theta\mid\theta_{n\varepsilon w}) L(θ∣θnεw),使得对于所有的 θ ∈ N ( θ n o w ) \theta\in \mathcal{N} ( \theta_\mathrm{now}) θ∈N(θnow),函数值 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 与 J ( θ ) J(\theta) J(θ) 足够接近。图9.2(b) 解释了做近似这一步。
第二步一一最大化:在置信域 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 中寻找变量 θ \theta θ 的值, 使得函数 L L L 的值最大化。把找到的值记作
θ n e w = a r g m a x θ ∈ N ( θ n o w ) L ( θ ∣ θ n o w ) . \theta_{\mathrm{new}}\:=\:\underset{\theta\in\mathcal{N}(\theta_{\mathrm{now}})}{\operatorname*{\mathrm{argmax}}}\:L(\boldsymbol{\theta}\mid\boldsymbol{\theta_{\mathrm{now}}})\:. θnew=θ∈N(θnow)argmaxL(θ∣θnow).
图 9.2( c) 解释了最大化这一步。
置信域方法其实是一类算法框架,而非一个具体的算法。有很多种方式实现实现置信域方法。第一步需要做近似,而做近似的方法有多种多样,比如蒙特卡洛、二阶泰勒展开。第二步需要解一个带约束的最大化问题;求解这个问题又需要单独的数值优化算法,比如梯度投影算法、拉格朗日法。除此之外,置信域 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 也有多种多样的选择, 既可以是球,也可以是两个概率分布的 KL 散度 (KL Divergence)。
ChatGPT对梯度投影算法的介绍
梯度投影算法的基本步骤可以通过数学公式进行介绍。考虑带有约束的优化问题:
m i n x f ( x ) min_{x} f(x) minxf(x)
其中 (f(x)) 是目标函数,(x) 是优化变量,同时满足一组约束条件:
g i ( x ) ≤ 0 , i = 1 , 2 , … , m g_i(x) \leq 0, \quad i = 1, 2, \ldots, m gi(x)≤0,i=1,2,…,m
梯度投影算法的迭代过程如下:
-
初始化: 选择初始解 ( x 0 x_0 x0),设置学习率 ( α \alpha α) 和停止准则。
-
梯度计算: 计算目标函数在当前解 ( x k x_k xk) 处的梯度 ( ∇ f ( x k ) \nabla f(x_k) ∇f(xk))。
-
梯度投影: 将梯度投影到满足约束条件的空间中。假设投影操作为 (P(x)),则更新方向为 ( Δ x k = P ( x k − α ∇ f ( x k ) ) − x k \Delta x_k = P(x_k - \alpha \nabla f(x_k)) - x_k Δxk=P(xk−α∇f(xk))−xk)。
-
更新变量: 使用投影后的梯度信息来更新变量 ( x k x_k xk):
x k + 1 = x k + α Δ x k x_{k+1} = x_k + \alpha \Delta x_k xk+1=xk+αΔxk
- 收敛判断: 判断算法是否达到停止条件,例如目标函数的变化足够小或者达到预定的迭代次数。
在这里,梯度投影的关键在于投影操作 (P(x)) 的定义。具体的投影形式取决于约束条件的性质。例如,对于线性约束 ( g i ( x ) ≤ 0 g_i(x) \leq 0 gi(x)≤0),投影操作可以表示为 ( P ( x ) = max ( 0 , g i ( x ) ) P(x) = \max(0, g_i(x)) P(x)=max(0,gi(x)))。对于更一般的非线性约束,可能需要使用专门的数学工具或算法来进行梯度投影。
需要注意的是,实际应用中可能需要根据具体问题对算法进行调整和定制。
策略学习
首先复习策略学习的基础知识。策略网络记作 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ), 它是个概率质量函数。动作价值函数记作 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a),它是回报的期望。状态价值函数记作
V π ( s ) = E A ∼ π ( ⋅ ∣ s ; θ ) [ Q π ( s , A ) ] = ∑ a ∈ A π ( a ∣ s ; θ ) ⋅ Q π ( s , a ) . ( 9.2 ) V_{\pi}(s)\:=\:\mathbb{E}_{A\sim\pi(\cdot|s;\theta)}\big[Q_{\pi}(s,A)\big]\:=\:\sum_{a\in\mathcal{A}}\pi(a|s;\boldsymbol{\theta})\cdot Q_{\pi}(s,a). \quad(9.2) Vπ(s)=EA∼π(⋅∣s;θ)[Qπ(s,A)]=a∈A∑π(a∣s;θ)⋅Qπ(s,a).(9.2)
注意, V π ( s ) V_{\pi}(s) Vπ(s) 依赖于策略网络 π, 所以依赖于 π \pi π 的参数 θ \theta θ。策略学习的目标函数是
J ( θ ) = E S [ V π ( S ) ] . ( 9.3 ) J(\boldsymbol{\theta})=\mathbb{E}_{S}\big[V_{\pi}(S)\big].\quad(9.3) J(θ)=ES[Vπ(S)].(9.3)
J ( θ ) J(\theta) J(θ) 只依赖于 θ \theta θ,不依赖于状态 S S S 和动作 A A A。前面介绍的策略梯度方法 (包括 REINFORCE 和 Actor-Critic) 用蒙特卡洛近似梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ), 得到随机梯度,然后做随机梯度上升更新 θ \theta θ,使得目标函数 J ( θ ) J(\theta) J(θ) 增大。
下面我们要把目标函数 J ( θ ) J(\boldsymbol{\theta}) J(θ) 变换成一种等价形式。从等式(9.2)出发,把状态价值写成
V π ( s ) = ∑ a ∈ A π ( a ∣ s ; θ n o w ) ⋅ π ( a ∣ s ; θ ) π ( a ∣ s ; θ n o w ) ⋅ Q π ( s , a ) = E A ∼ π ( ⋅ ∣ s ; θ n o w ) [ π ( A ∣ s ; θ ) π ( A ∣ s ; θ n o w ) ⋅ Q π ( s , A ) ] . ( 9.4 ) \begin{gathered} V_{\pi}(s) =\:\sum_{a\in\mathcal{A}}\pi\big(a\big|\:s;\:\theta_{\mathrm{now}}\big)\:\cdot\:\frac{\pi(a\:|\:s;\:\boldsymbol{\theta})}{\pi(a\:|s;\:\boldsymbol{\theta}_{\mathrm{now}})}\:\cdot\:Q_{\pi}(s,a) \\ =\quad\mathbb{E}_{A\sim\pi(\cdot|s;\theta_{\mathrm{now}})}\bigg[\:\frac{\pi(A\:|\:s;\:\boldsymbol{\theta})}{\pi(A\:|\:s;\:\boldsymbol{\theta}_{\mathrm{now}})}\:\cdot\:Q_{\pi}(s,A)\:\bigg]. \end{gathered}\quad(9.4) Vπ(s)=a∈A∑π(a s;θnow)⋅π(a∣s;θnow)π(a∣s;θ)⋅Qπ(s,a)=EA∼π(⋅∣s;θnow)[π(A∣s;θnow)π(A∣s;θ)⋅Qπ(s,A)].(9.4)
第一个等式很显然,因为连加中的第一项可以消掉第二项的分母。第二个等式把策略网络 π ( A ∣ s ; θ n o w ) \pi(A|s;\boldsymbol{\theta}_\mathrm{now}) π(A∣s;θnow) 看做动作 A A A 的概率质量函数,所以可以把连加写成期望。由公式 (9.3) 与(9.4) 可得定理 9.1。定理 9.1 是 TRPO 的关键所在,甚至可以说 TRPO 就是从这个公式推出的。

定理 9.1. 目标函数的等价形式目标函数 J ( θ ) J(\theta) J(θ)可以等价写成:
J ( θ ) = E S [ E A ∼ π ( ⋅ ∣ S , θ n o w ) [ π ( A ∣ S ; θ ) π ( A ∣ S ; θ n o w ) ⋅ Q π ( S , A ) ] ] . J(\boldsymbol{\theta})\:=\:\mathbb{E}_{S}\bigg[\mathbb{E}_{A\sim\pi(\cdot|S,\boldsymbol{\theta}_{\mathrm{now}})}\bigg[\frac{\pi(A\:|\:S;\:\boldsymbol{\theta})}{\pi(A\:|\:S;\:\boldsymbol{\theta}_{\mathrm{now}})}\:\cdot\:Q_{\pi}(S,A)\bigg]\bigg]. J(θ)=ES[EA∼π(⋅∣S,θnow)[π(A∣S;θnow)π(A∣S;θ)⋅Qπ(S,A)]].
上面 Q π Q_\pi Qπ 中的 π \pi π 指的是 π ( A ∣ S ; θ ) \pi(A|S;\boldsymbol{\theta}) π(A∣S;θ)。
公式中的期望是关于状态 S S S 和动作 A A A 求的。状态 S S S 的概率密度函数只有环境知道, 而我们并不知道,但是我们可以从环境中获取 S S S 的观测值。动作 A A A 的概率质量函数是策略网络 π ( A ∣ S ; θ n o w ) \pi(A|S;\theta_\mathrm{now}) π(A∣S;θnow); 注意,策略网络的参数是旧的值 θ n o w \theta_\mathrm{now} θnow.
TRPO 数学推导
前面介绍了数值优化的基础和价值学习的基础,终于可以开始推导 TRPO。TRPO 是置信域方法在策略学习中的应用,所以 TRPO 也遵循置信域方法的框架,重复做近似和最大化这两个步骤,直到算法收敛。收敛指的是无法增大目标函数 J ( θ ) J(\theta) J(θ) , 即无法增大期望回报。
第一步——做近似:
我们从定理 9.1 出发。定理把目标函数 J ( θ ) J(\theta) J(θ) 写成了期望的形式。我们无法直接算出期望,无法得到 J ( θ ) J(\theta) J(θ) 的解析表达式;原因在于只有环境知道状态 S S S 的概率密度函数,而我们不知道。我们可以对期望做蒙特卡洛近似,从而把函数 J J J 近似成函数 L L L。用策略网络 π ( A ∣ S ; θ n o w ) \pi(A|S;\theta_\mathrm{now}) π(A∣S;θnow) 控制智能体跟环境交互,从头到尾玩完一局游戏观测到一条轨迹:
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , ⋯ , s n , a n , r n . s_1,\:a_1,\:r_1,\:s_2,\:a_2,\:r_2,\:\cdots,\:s_n,\:a_n,\:r_n. s1,a1,r1,s2,a2,r2,⋯,sn,an,rn.
其中的状态 { s t } t = 1 n \{s_t\}_{t=1}^n {st}t=1n 都是从环境中观测到的,其中的动作 { a t } t = 1 n \{a_t\}_{t=1}^n {at}t=1n 都是根据策略网络 π ( ⋅ ∣ s t ; θ n o w ) \pi(\cdot|s_t;\theta_\mathrm{now}) π(⋅∣st;θnow) 抽取的样本。所以,
π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ n o w ) ⋅ Q π ( s t , a t ) ( 9.5 ) \frac{\pi(a_t\mid s_t;\boldsymbol{\theta})}{\pi(a_t\mid s_t;\boldsymbol{\theta_\mathrm{now}})}\cdot Q_\pi(s_t,a_t) \quad(9.5) π(at∣st;θnow)π(at∣st;θ)⋅Qπ(st,at)(9.5)
是对定理 9.1 中期望的无偏估计。我们观测到了 n n n 组状态和动作,于是应该对公式 (9.5) 求平均,把得到均值记作:
L ( θ ∣ θ n o w ) = 1 n ∑ t = 1 n π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ n o w ) ⋅ Q π ( s t , a t ) ⏟ 定理 9.1 中期望的无偏估计 . ( 9.6 ) L(\boldsymbol{\theta}\:|\:\boldsymbol{\theta_\mathrm{now}})\:=\:\frac{1}{n}\sum_{t=1}^{n}\underbrace{\frac{\pi(a_{t}\:|\:s_{t};\boldsymbol{\theta})}{\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta_\mathrm{now}}\:)}\:\cdot\:Q_{\pi}\left(s_{t},a_{t}\right)}_{定理 9.1 中期望的无偏估计}\:.\quad(9.6) L(θ∣θnow)=n1t=1∑n定理9.1中期望的无偏估计 π(at∣st;θnow)π(at∣st;θ)⋅Qπ(st,at).(9.6)
既然连加里每一项都是期望的无偏估计,那么 n n n 项的均值 L L L 也是无偏估计。所以可以拿 L L L作为目标函数 J J J 的蒙特卡洛近似。
公式(9.6) 中的 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 是对目标函数 J ( θ ) J(\theta) J(θ) 的近似。可惜我们还无法直接对 L L L 求最大化,原因是我们不知道动作价值 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at)。解决方法是做两次近似:
Q π ( s t , a t ) ⟹ Q π o l d ( s t , a t ) ⟹ u t . Q_{\pi}(s_{t},a_{t})\quad\Longrightarrow\quad Q_{\pi_{\mathrm{old}}}(s_{t},a_{t})\quad\Longrightarrow\quad u_{t}. Qπ(st,at)⟹Qπold(st,at)⟹ut.
公式中 Q π Q_\pi Qπ 中的策略是 π ( a t ∣ s t ; θ ) \pi(a_t\mid s_t;\boldsymbol{\theta}) π(at∣st;θ), 而 Q π o l d Q_\mathrm{\pi_\mathrm{old}} Qπold 中的策略则是旧策略 π ( a t ∣ s t ; θ n o w ) \pi(a_t\mid s_t;\boldsymbol{\theta_\mathrm{now}}) π(at∣st;θnow)。我们用旧策略 π ( a t ∣ s t ; θ n o w ) \pi(a_t\mid s_t;\theta_\mathrm{now}) π(at∣st;θnow)生成轨迹 { ( s j , a j , r j , s j + 1 ) } j = 1 n \{(s_j,a_j,r_j,s_{j+1})\}_{j=1}^n {(sj,aj,rj,sj+1)}j=1n。所以折扣回报
u t = r t + γ ⋅ r t + 1 + γ 2 ⋅ r t + 2 + ⋯ + γ n − t ⋅ r n u_{t}\:=\:r_{t}+\gamma\cdot r_{t+1}+\gamma^{2}\cdot r_{t+2}+\cdots+\gamma^{n-t}\cdot r_{n} ut=rt+γ⋅rt+1+γ2⋅rt+2+⋯+γn−t⋅rn
是对 Q π o l d Q_\mathrm{\pi_\mathrm{old}} Qπold 的近似,而未必是对 Q π Q_\mathrm{\pi} Qπ 的近似。仅当 θ \theta θ接近 θ r o w \theta_\mathrm{row} θrow 的时候, u t u_t ut 才是 Q π Q_\pi Qπ 的有效近似。这就是为什么要强调置信域,即 θ \theta θ在 θ n o w \theta_\mathrm{now} θnow的邻域中。
拿 u t u_t ut 替代 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at),那么公式(9.6) 中的 L ( θ ∣ θ n o w ) L(\theta|\theta_\mathrm{now}) L(θ∣θnow) 变成了
L ~ ( θ ∣ θ n o w ) = 1 n ∑ t = 1 n π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ n o w ) ⋅ u t . ( 9.7 ) \boxed{\quad\tilde{L}(\boldsymbol{\theta}\mid\boldsymbol{\theta}_{\mathrm{now}})=\frac1n\sum_{t=1}^n\frac{\pi(a_t\mid s_t;\boldsymbol{\theta})}{\pi(a_t\mid s_t;\boldsymbol{\theta}_{\mathrm{now}})}\cdot u_t.}\quad(9.7) L~(θ∣θnow)=n1t=1∑nπ(at∣st;θnow)π(at∣st;θ)⋅ut.(9.7)
总结一下,我们把目标函数 J J J 近似成 L L L,然后又把 L L L 近似成 L ~ \tilde{L} L~。在第二步近似中,我们需要假设 θ \theta θ 接近 θ n o w \theta_\mathrm{now} θnow。
第二步——最大化:
TRPO 把公式 (9.7) 中的 L ~ ( θ ∣ θ n o w ) \tilde{L}(\theta|\theta_\mathrm{now}) L~(θ∣θnow) 作为对目标函数 J ( θ ) J(\theta) J(θ) 的近似,然后求解这个带约束的最大化问题:
max θ L ~ ( θ ∣ θ n o w ) ; s . t . θ ∈ N ( θ n o w ) . ( 9.8 ) \boxed{\max_{\theta}\tilde{L}\left(\boldsymbol{\theta}\mid\boldsymbol{\theta}_{\mathrm{now}}\right);\quad\mathrm{s.t.~}\boldsymbol{\theta}\in\mathcal{N}(\boldsymbol{\theta}_{\mathrm{now}}).}\quad(9.8) θmaxL~(θ∣θnow);s.t. θ∈N(θnow).(9.8)
公式中的 N ( θ n o w ) \mathcal{N} ( \theta_\mathrm{now}) N(θnow) 是置信域,即 θ n o w \theta_\mathrm{now} θnow的一个邻域。该用什么样的置信域呢?
- 一种方法是用以 θ n o w \theta_\mathrm{now} θnow为球心、以 Δ \Delta Δ为半径的球作为置信域。这样的话,公式(9.8)就变成
max θ L ~ ( θ ∣ θ n o w ) ; s.t. ∥ θ − θ n o w ∥ 2 ≤ Δ . ( 9.9 ) \max_{\boldsymbol{\theta}}\:\tilde{L}(\boldsymbol{\theta}\:|\:\boldsymbol{\theta}_{\mathrm{now}});\quad\text{s.t.}\:\left\|\boldsymbol{\theta}-\boldsymbol{\theta}_{\mathrm{now}}\right\|_2\leq\Delta.\quad(9.9) θmaxL~(θ∣θnow);s.t.∥θ−θnow∥2≤Δ.(9.9)
- 另一种方法是用 KL 散度衡量两个概率质量函数—— π ( ⋅ ∣ s i ; θ n o w ) \pi(\cdot|s_i;\theta_\mathrm{now}) π(⋅∣si;θnow) 和 π ( ⋅ ∣ s i ; θ ) \pi(\cdot|s_i;\theta) π(⋅∣si;θ)—— 的距离。两个概率质量函数区别越大,它们的 KL 散度就越大。反之,如果 θ \theta θ 很接近 θ n o w \theta_\mathrm{now} θnow,那么两个概率质量函数就越接近。用 KL 散度的话,公式(9.8)就变成
max θ L ~ ( θ ∣ θ n o w ) ; s . t . 1 t ∑ i = 1 t KL [ π ( ⋅ ∣ s i ; θ n o w ) ∥ π ( ⋅ ∣ s i ; θ ) ] ≤ Δ . ( 9.10 ) \max_{\boldsymbol{\theta}}\tilde{L}\left(\boldsymbol{\theta}\mid\boldsymbol{\theta}_{\mathrm{now}}\right);\quad\mathrm{s.t.}\:\frac{1}{t}\sum_{i=1}^{t}\:\text{KL}\Big[\:\pi\big(\:\cdot\:\big|\:s_{i};\:\boldsymbol{\theta}_{\mathrm{now}}\big)\:\big\Vert\:\pi\big(\:\cdot\:\big|\:s_{i};\:\boldsymbol{\theta}\big)\:\Big]\:\le\:\Delta. \quad(9.10) θmaxL~(θ∣θnow);s.t.t1i=1∑tKL[π(⋅ si;θnow) π(⋅ si;θ)]≤Δ.(9.10)
用球作为置信域的好处是置信域是简单的形状,求解最大化问题比较容易,但是用球做置信域的实际效果不如用 KL 散度。
TRPO 的第二步—最大化——需要求解带约束的最大化问题(9.9) 或者 (9.10)。注意,这种问题的求解并不容易;简单的梯度上升算法并不能解带约束的最大化问题。数值优化教材通常有介绍带约束问题的求解,有兴趣的话自己去阅读数值优化教材,这里就不详细解释如何求解问题 (9.9) 或者 (9.10)。读者可以这样看待优化问题:只要你能把一个优化问题的目标函数和约束条件解析地写出来,通常会有数值算法能解决这个问题。
训练流程
在本节的最后,我们总结一下用 TRPO 训练策略网络的流程。TRPO 需要重复做近似和最大化这两个步骤:
- 做近似——构造函数 L ~ \tilde{L} L~ 近似目标函数 J ( θ ) : J(\theta): J(θ):
(a). 设当前策略网络参数是 θ n o w \theta_\mathrm{now} θnow。用策略网络 π ( a ∣ s ; θ n o w ) \pi(a\mid s;\theta_\mathrm{now}) π(a∣s;θnow) 控制智能体与环境交互,玩完一局游戏,记录下轨迹:
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , ⋯ , s n , a n , r n . s_{1},\:a_{1},\:r_{1},\:s_{2},\:a_{2},\:r_{2},\:\cdots,\:s_{n},\:a_{n},\:r_{n}. s1,a1,r1,s2,a2,r2,⋯,sn,an,rn.
(b). 对于所有的 t = 1 , ⋯ , n t=1,\cdots,n t=1,⋯,n, 计算折扣回报 u t = ∑ k = t n γ k − t ⋅ r k u_t=\sum_{k=t}^n\gamma^{k-t}\cdot r_k ut=∑k=tnγk−t⋅rk.
(c ). 得出近似函数:
L ~ ( θ ∣ θ n o w ) = 1 n ∑ t = 1 n π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ n o w ) ⋅ u t . \tilde{L}\left(\boldsymbol{\theta}\:|\:\boldsymbol{\theta}_{\mathrm{now}}\right)\:=\:\frac{1}{n}\sum_{t=1}^{n}\frac{\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta})}{\pi(a_{t}\:|\:s_{t};\boldsymbol{\theta}_{\mathrm{now}})}\:\cdot\:u_{t}. L~(θ∣θnow)=n1t=1∑nπ(at∣st;θnow)π(at∣st;θ)⋅ut.
- 最大化——用某种数值算法求解带约束的最大化问题:
θ n e w = a r g m a x L ~ ( θ ∣ θ n o w ) ; s . t . ∥ θ − θ n o w ∥ 2 ≤ Δ . \theta_{\mathrm{new}}\:=\:\mathrm{argmax}\:\tilde{L}(\boldsymbol{\theta}\:|\:\theta_{\mathrm{now}});\quad\mathrm{s.t.}\:\left\|\theta-\theta_{\mathrm{now}}\right\|_{2}\:\leq\:\Delta. θnew=argmaxL~(θ∣θnow);s.t.∥θ−θnow∥2≤Δ.
此处的约束条件是二范数距离。可以把它替换成 KL 散度,即公式 (9.10)。
TRPO 中有两个需要调的超参数:一个是置信域的半径 Δ \Delta Δ, 另一个是求解最大化问题的数值算法的学习率。通常来说, Δ \Delta Δ 在算法的运行过程中要逐渐缩小。虽然 TRPO 需要调参,但是 TRPO 对超参数的设置并不敏感。即使超参数设置不够好,TRPO 的表现也不会太差。相比之下,策略梯度算法对超参数更敏感。
TRPO 算法真正实现起来并不容易,主要难点在于第二步一一最大化。不建议读者自己去实现 TRPO。
后记
截至2024年1月30日16点52分,完成王树森的深度强化学习视频课程。后面的多智能体部分听完了两节课,但是没有做相应的笔记。
回顾这几天的学习:2024年1月25日晚上闲来无事确定学习王树森的这门课,2024年1月26日正式开始学习,截至2024年1月30日,总共花费5天时间学习深度强化学习。形成了系列笔记。
后续可能会跟进动手学强化学习这门课。
2024年1月31日坐高铁回家过年,在回家之前完成了自己设定的计划——学习完王树森的《深度强化学习》。看到TODO list上又完成了一件事,整个人还是比较开心的。
2024春节快乐。
相关文章:

深度强化学习(王树森)笔记11
深度强化学习(DRL) 本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。 参考链接 Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL 源代码链接:https://github.c…...

python 实现 macOS状态栏 网速实时显示
安装依赖包: pip install pillow psutil rumpsnetSpeedApp.py from PIL import Image, ImageDraw, ImageFont import psutil import rumpsclass NetSpeedApp(rumps.App):def __init__(self):super(NetSpeedApp, self).__init__("NetSpeed")self.titlese…...

【C++】开源:Windows图形库EasyX配置与使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍Windows图形库EasyX配置与使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下&#…...

微信小程序 全局变量键值对map对象
在微信小程序中,键值对的map对象通常用于存储和操作键值对的集合。以下是一些常见的操作: 创建map对象 在JavaScript中,可以通过对象字面量语法或者使用new Map()来创建map对象 // 使用对象字面量 var map {key1: value1,key2: value2 };…...
20240131在WIN10下配置whisper
20240131在WIN10下配置whisper 2024/1/31 18:25 首先你要有一张NVIDIA的显卡,比如我用的PDD拼多多的二手GTX1080显卡。【并且极其可能是矿卡!】800¥ 2、请正确安装好NVIDIA最新的545版本的驱动程序和CUDA。 2、安装Torch 3、配置whisper http…...
3338 蓝桥杯 wyz的数组IV 简单
3338 蓝桥杯 wyz的数组IV 简单 //C风格解法1,通过率50% #include<bits/stdc.h>int main(){std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int n; std::cin >> n;int ans 0;std::vector<int>a(n);for(auto &am…...

git Filename too long
git Filename too long 原因: 文件名限制260长度 解决:全局配置git git config --system core.longpaths true查看: git config --get core.longpaths...
MySQL数据库-理论基础
1.1 什么是数据库 数据: 描述事物的符号记录, 可以是数字、 文字、图形、图像、声音、语言等,数据有多种形式,它们都可以经过数字化后存入计算机。 数据库: 存储数据的仓库,是长期存放在计算机内、有组织…...
立体边界,让arcgis出图更酷炫一些
就是这样子的那个图—— 本期我们还是用长沙市为例, 来手把手的演示制作立体边界, 就是这个样子的边界—— 第一步—准备底图 其实你准备什么底图都可以哈,例如调用天地图、下载个影像图,或者用其他什么的底图,都是…...
【C++】 C++入门—内联函数
C入门 1 内联函数1.1 定义1.2 查看方式1.3 注意 Thanks♪(・ω・)ノ谢谢阅读下一篇文章见!!! 1 内联函数 1.1 定义 程序在执行一个函数前需要做准备工作:要将实参、局部变量、返回地址以及若干寄存…...

软件工程知识梳理2-需求分析
需求分析时软件定义的最后一个阶段,它的基本任务时准确回答系统必须做什么的问题。 输出:本阶段必须的输出时软件需求规格说明书。 角色:需求分析员 参与者:用户、需求分析员 需求分析遵循的准则: 必须理解并描述问…...
mac裁剪图片
今天第一次用mac裁剪图片,记录一下过程,差点我还以为我要下载photoshop了, 首先准备好图片 裁剪的目的是把图片的标题给去掉,但是不能降低分辨率,否则直接截图就可以了 解决办法 打开原始图片(不要使用预览…...
 | Box,Surface - 帧布局)
Compose | UI组件(十) | Box,Surface - 帧布局
文章目录 前言Box 组件的参数说明Box 组件的使用Surface 的参数说明Surface 的使用 总结 前言 Box组件是 按子组件依次叠加 的布局组件,相当传统View中的 FrameLayout Box 组件的参数说明 Composable inline fun Box(modifier: Modifier Modifier, …...

种草日记|林曦老师的冬日好物分享
冬天将尽春天就要来了,换季的时候最容易引起皮肤干燥、头发毛躁不舒服的问题,今天就来说说林曦老师推荐的冬日护理爱用好物。大家都要“如婴儿乎”,照顾好自己哦~ 1、Aco甘油保湿霜 Aco甘油保湿霜好大一罐&#x…...
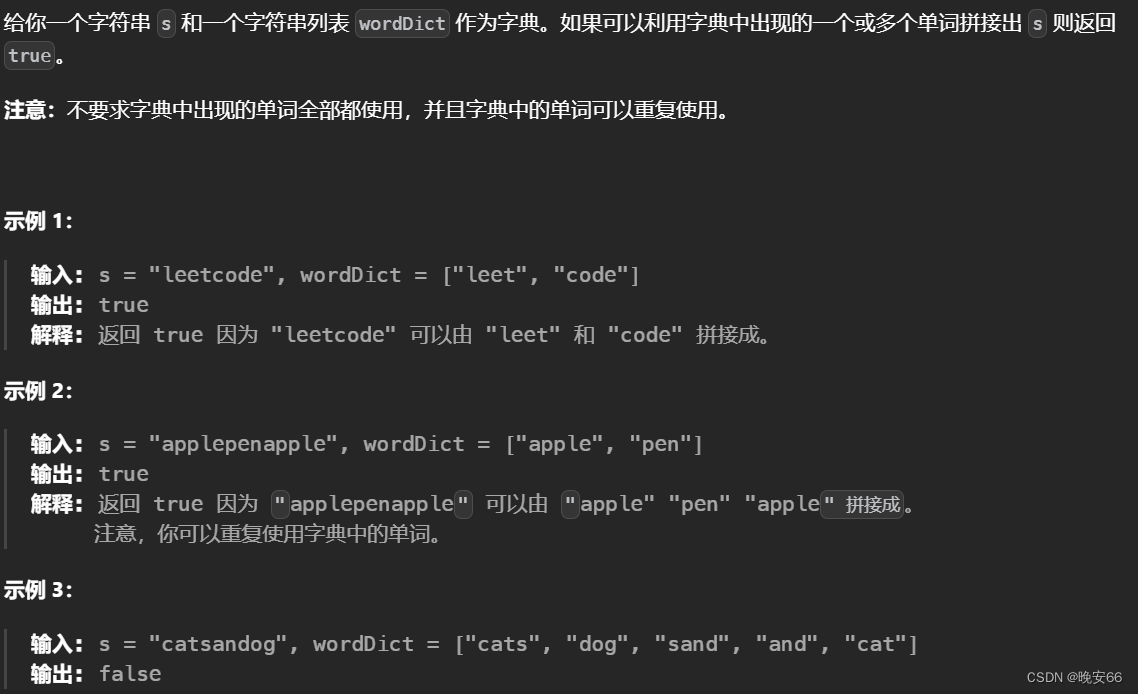
【算法与数据结构】139、LeetCode单词拆分
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题可以看做一个动态规划问题。其中,字符串s是背包,而字典中的单词就是物品。…...

NLP任务之Named Entity Recognition
深度学习的实现方法: 双向长短期记忆网络(BiLSTM): BiLSTM是一种循环神经网络(RNN)的变体,能够捕捉序列数据中的长期依赖关系。在NER任务中,BiLSTM能有效地处理文本序列,捕捉前后文本…...

NUXT3项目实践总结
目录 一、NUXT3实现黑夜白天模式切换 需求 实现 效果 二、scrollreveal插件实现动画效果 需求 实现 封装 使用 文档 效果 三、useSeoMeta的使用 作用 使用 效果 四、NUXT3开启代理 使用 注意 五、$fetch、useFetch 、useAsyncData的区别 六、错误页面处理 …...

中科星图——2020年全球30米地表覆盖精细分类产品V1.0(29个地表覆盖类型)
数据名称: 2020年全球30米地表覆盖精细分类产品V1.0 GLC_FCS30 长时序 地表覆盖 动态监测 全球 数据来源: 中国科学院空天信息创新研究院 时空范围: 2015-2020年 空间范围: 全球 数据简介: 地表覆盖分布…...
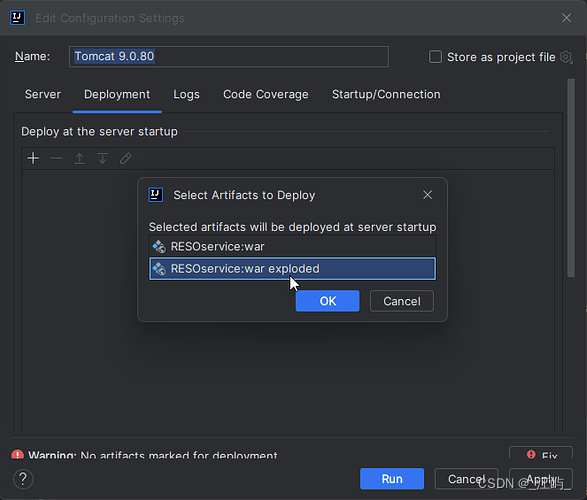
Tomcat 部署项目时 war 和 war exploded区别
在 Tomcat 调试部署的时候,我们通常会看到有下面 2 个选项。 是选择war还是war exploded 这里首先看一下他们两个的区别: war 模式:将WEB工程以包的形式上传到服务器 ;war exploded 模式:将WEB工程以当前文件夹的位置…...

【开源】SpringBoot框架开发天然气工程运维系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统角色分类2.2 核心功能2.2.1 流程 12.2.2 流程 22.3 各角色功能2.3.1 系统管理员功能2.3.2 用户服务部功能2.3.3 分公司(施工单位)功能2.3.3.1 技术员角色功能2.3.3.2 材料员角色功能 2.3.4 安…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
