9.2爬楼梯(LC70-E)

算法:
多举几个例子,找规律:
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层(时序)。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
动规五部曲:
1.确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方
2.确定递推公式(实在不行,多举几个例子推导一下)
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来(题目中说,每次可以爬1/2个阶梯)。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么(dp[i - 1]种方法)。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么(dp[i - 2]种方法)。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
dp[i] = dp[i - 1] + dp[i - 2] 。
3.dp数组如何初始化

题目中说了n从1开始
dp[1] = 1,dp[2] = 2
然后从i = 3开始递推
4.确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
5.举例推导dp数组(主要用于debug)
当n为5的时候,dp table(dp数组)应该是这样的
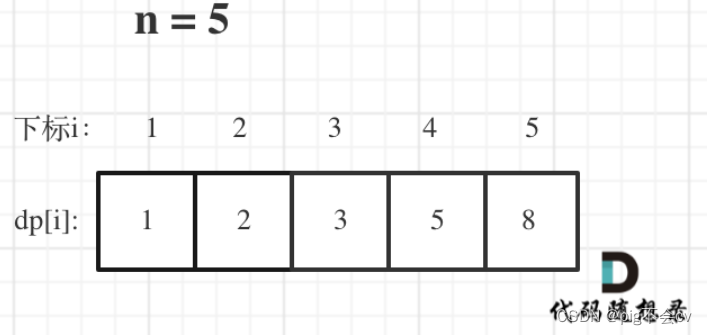
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
正确代码:
class Solution {public int climbStairs(int n) {int[] dp = new int[n+1];if (n<=2){return n;}dp[1] = 1;dp[2] = 2;for (int i=3 ;i<=n; i++){dp[i] = dp[i-1] +dp[i-2];}return dp[n];}
}时间空间复杂度:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
相关文章:

9.2爬楼梯(LC70-E)
算法: 多举几个例子,找规律: 爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。 那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层(时序)。 所以到第三层楼梯的状态可以由…...

Asp.net移除Server, X-Powered-By, 和X-AspNet-Version头
移除X-AspNet-Version很简单,只需要在Web.config中增加这个配置节: <httpRuntime enableVersionHeader"false" />移除Server在Global.asax文件总增加: //隐藏IIS版本 protected void Application_PreSendRequestHeaders() {HttpContext.Current.Res…...

reactnative 调用原生ui组件
reactnative 调用原生ui组件 1.该样例已textView,介绍。 新建MyTextViewManager 文件,继承SimpleViewManager。import android.graphics.Color; import andr…...

面试手写第五期
文章目录 一. 实现一个函数用来对 URL 的 querystring 进行编码二. 如何实现一个数组洗牌函数 shuffle三. 异步加法的几种方式四. 实现trim函数五. 求多个数组的交集六. 手写实现render函数七. 驼峰转- -转驼峰八. instanceof实现九. 组合问题十. 字符串分组 一. 实现一个函数用…...

【CSS】css选择器和css获取第n个元素(:nth-of-type(n)、:nth-child(n)、first-child和last-child)
:nth-of-type、:nth-child的区别 一、css选择器二、:nth-of-type、:nth-child的区别:nth-of-type(n):选择器匹配属于父元素的特定类型的第N个子元素:nth-child(n):选择器匹配属于其父元素的第 N 个子元素,不论元素的类型:first-child…...
解析Excel文件内容,按每列首行元素名打印出某个字符串的统计占比(超详细)
目录 1.示例: 1.1 实现代码1:列数为常量 运行结果: 1.2 实现代码2:列数为变量 运行结果: 1.示例: 开发需求:读取Excel文件,统计第3列到第5列中每列的"False"字段占…...
qt中遇到[Makfile.Debug:119:debug/app.res.o] Error 1的原因以及解决方法
当我们将项目已到本地qt环境中会出现下图的代码错误 解决方法:在主界面中,点击左边的项目栏,选择构建设置,看Shadow build下面的路径是否为中文,改成英文,或者直接将Shadow build这个 √ 去掉就行了,如图已…...

pytorch调用gpu训练的流程以及示例
首先需要确保系统上安装了CUDA支持的NVIDIA GPU和相应的驱动程序。 基本步骤如下 检查CUDA是否可用: 使用 torch.cuda.is_available() 来检查CUDA是否可用。 指定设备: 可以使用 torch.device(“cuda:0”) 来指定要使用的GPU。如果系统有多个GPU&…...
学习Android的第一天
目录 什么是 Android? Android 官网 Android 应用程序 Android 开发环境搭建 Android 平台架构 Android 应用程序组件 附件组件 Android 第一个程序 HelloWorld 什么是 Android? Android(发音为[ˈnˌdrɔɪd],非官方中文…...

回归预测 | Matlab实现CPO-LSTM【24年新算法】冠豪猪优化长短期记忆神经网络多变量回归预测
回归预测 | Matlab实现CPO-LSTM【24年新算法】冠豪猪优化长短期记忆神经网络多变量回归预测 目录 回归预测 | Matlab实现CPO-LSTM【24年新算法】冠豪猪优化长短期记忆神经网络多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现CPO-LSTM【24年新算…...
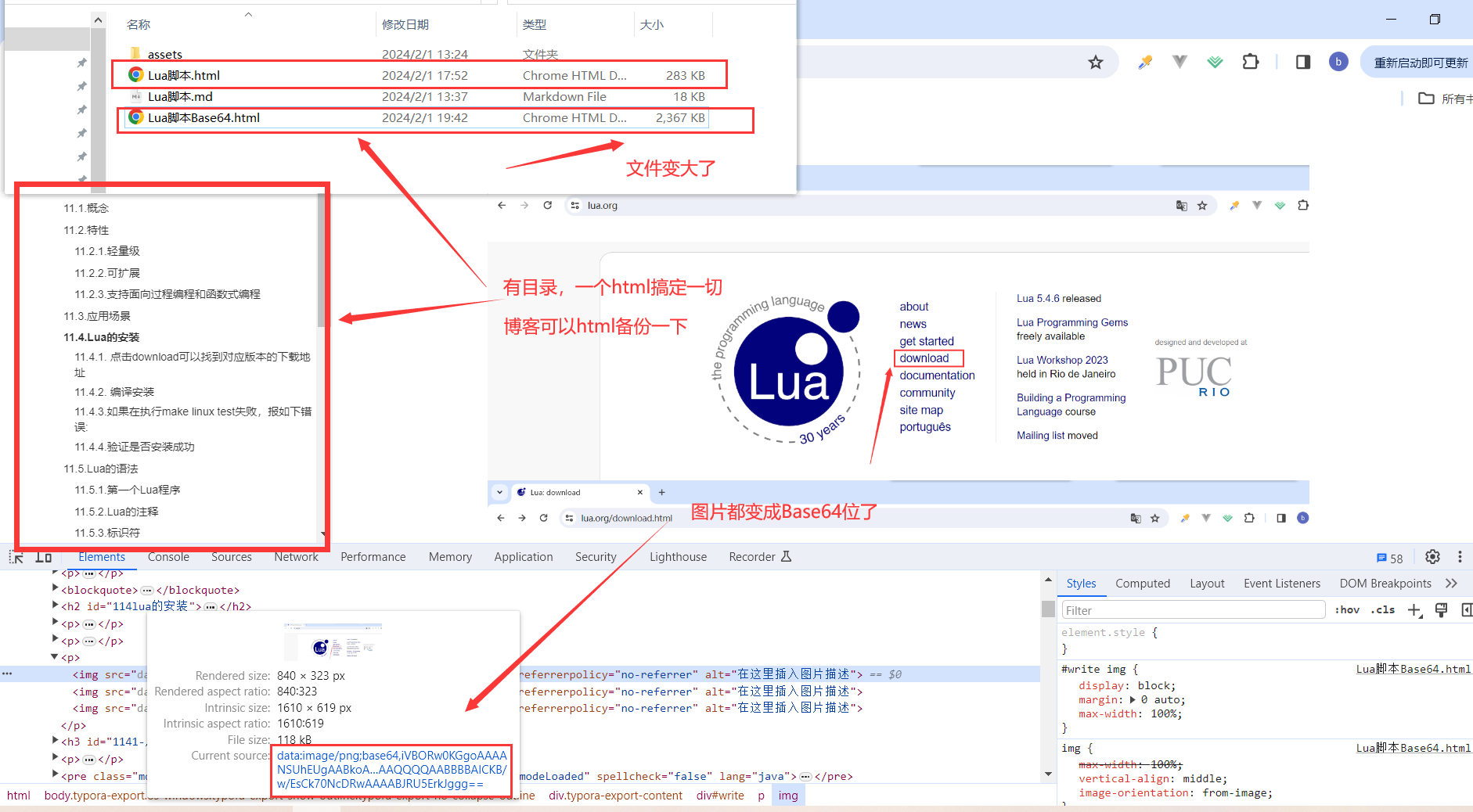
Typora导出html文件图片自动转换成base64
Typora导出html文件图片自动转换成base64 一、出现问题二、解决方案三、编码实现3.1.创建Java项目3.2.代码3.3.打包成Jar包 四、如何使用endl 一、出现问题 typora 导出 html 的时候必须带有原图片,不方便交流学习,文件太多显得冗余,只有将图…...

『C++成长记』string使用指南
🔥博客主页:小王又困了 📚系列专栏:C 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、string类介绍 二、string类的常用接口说明 📒2.1string类对象的常…...

硬件连通性测试:构建数字世界的无形基石
在当今数字化的时代,硬件设备的连通性对于系统的正常运行至关重要。硬件连通性测试作为确保设备协同工作的关键步骤,扮演着构建数字世界的无形基石的角色。本文将深入探讨硬件连通性测试的意义、方法以及在现代科技生态系统中的重要性。 1. 硬件连通性测…...
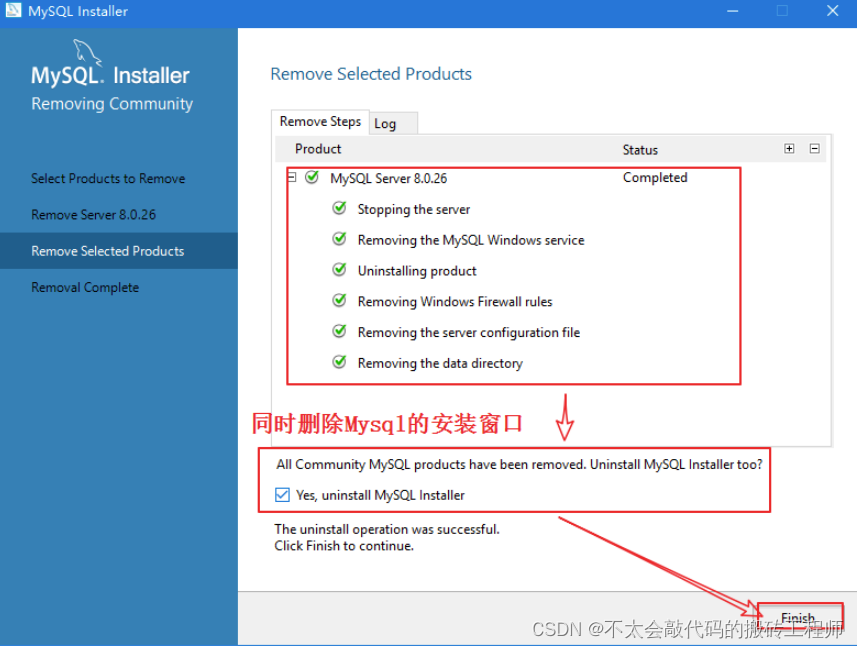
mysql的安装与卸载
mysql的安装 mysql 8.0的安装步骤: 1. 从mysql官网上下载mysql安装软件 https://www.mysql.com/ 2. 双击msi文件进行安装 3. 选择安装的类型 选择server only可以远程访问数据库 4. 选择服务并安装 5. 安装中,安装完成后直接next 6. 进入mysql的配置 …...

假期作业 2.2
第一章 命名空间 一.选择题 1、编写C程序一般需经过的几个步骤依次是( B ) A. 编辑、调试、编译、连接 B. 编辑、编译、连接、运行 C. 编译、调试、编辑、连接 D. 编译、编辑、连接、运行 2、所谓数据封装就是将一组数据和与这组数…...

运维SRE-02 正则表达式、grep
1.特殊符号补充 1.1位置相关的特殊符号 . 当前目录 .. 当前目录的上级目录 ~ 当前用户家目录 / 根目录 cd - 返回上次所在目录1.2熟练掌握 # 注释符号,root命令提示符 | 管道符号.1.3了解其他特殊符号 $ 取值(取出变量的值),普通用户的提示符 ! % ^ & * (){} [] ; ? \…...
【SpringCloud】使用OpenFeign进行微服务化改造
目录 一、需求与背景二、OpenFeign 远程调用技术原理三、项目代码演示3.1 引入依赖3.2 实现OpenFeign注解修饰接口3.3 指定 OpenFeign 远程调用接口的扫描路径 四、OpenFeign 在日志中打印Request和Response五、OpenFeign 客户端超时配置六、使用 OpenFeign 实现服务降级6.1 实…...
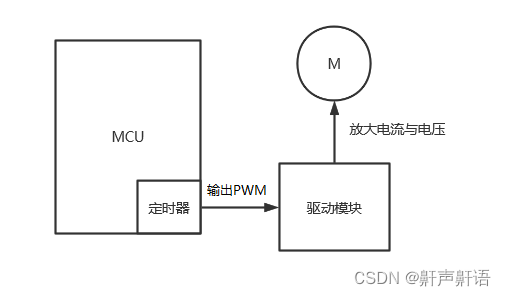
DRV8313和L298N都是电机驱动,一个是驱动三相FOC无刷直流电机的,一个是驱动有刷电机,使stm32控制无刷电机简单入门知识
DRV8313和L298N都是电机驱动器,但它们之间存在一些关键的区别: DRV83131: 由德州仪器(TI)制造。 具有集成的场效应晶体管(FET)。 最大电压为65V。 峰值电流为3A。 适用于三相电机驱动。 L298N…...

React16源码: React中event事件系统初始化源码实现
event 事件系统初始化 1 )概述 react事件系统比较的复杂,它是基于dom的事件系统在dom事件系统上面进行了一个深度的封装它里面的很多实现逻辑都是自由的一套在初始化 react-dom 的源码的时候,会为react的事件系统注入 reactdom 相关的一些插…...

Qt6入门教程 15:QRadioButton
目录 一.简介 二.常用接口 三.实战演练 1.径向渐变 2.QSS贴图 3.开关效果 4.非互斥 一.简介 QRadioButton控件提供了一个带有文本标签的单选按钮。 QRadioButton是一个可以切换选中(checked)或未选中(unchecked)状态的选项…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
