状态压缩 笔记
棋盘式的f[i][j]中表示状态的j可以是状态本身也可以是在合法状态state中的下标
用状态本身比较方便,用下标比较省空间
用下标的话可以开id[M]数组记录一下
蒙德里安的梦想
求把 N×M的棋盘分割成若干个 1×2的长方形,有多少种方案。
例如当 N=2,M=4时,共有 5 种方案。当 N=2,M=3时,共有 3 种方案。
如下图所示:
![]()
输入格式
输入包含多组测试用例。
每组测试用例占一行,包含两个整数 N和 M。
当输入用例 N=0,M=0时,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个结果,每个结果占一行。
数据范围
1≤N,M≤11
输入样例:
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例:
1
0
1
2
3
5
144
51205先放横着的,空位竖着的就只有一种摆法
f[i][j]表示前i-1列已摆好,j表示第i列中有哪些行是凸出来的
核心思路是看第i-1行是否合法
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 12, M = 1 << 11;int n, m;
ll f[N][M];//前i-1列已摆好,第i列中有哪些行是凸出来的
vector<int> state[M];
bool st[M];int main()
{IOSwhile(cin >> n >> m, n){for(int i = 0; i < 1 << n; i ++)//处理合法状态 {st[i] = true;int cnt = 0;for(int j = 0; j < n; j ++){if(i >> j & 1){if(cnt % 2){st[i] = false;break;}cnt = 0;}else cnt ++;}if(cnt % 2)st[i] = false;}for(int i = 0; i < 1 << n; i ++) {state[i].clear();for(int j = 0; j < 1 << n; j ++){if((i & j) == 0 && st[i | j]){state[i].push_back(j);}}}memset(f, 0, sizeof f);f[0][0] = 1;for(int i = 1; i <= m; i ++){for(int j = 0; j < 1 << n; j ++)//i-1 i{for(auto k : state[j])//i-2 i-1{//核心是看i-1列是否合法 f[i][j] += f[i - 1][k];}}}cout << f[m][0] << endl;}return 0;
}最短Hamilton路径
给定一张 n 个点的带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 00 到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n行每行 n 个整数,其中第 i 行第 j 个整数表示点 i 到 j 的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x]并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤1e7
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18f[state][j],state表示哪些点走过,j表示当前停留在哪个点
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 20, M = 1 << N;int n;
int f[M][N], w[N][N];int main()
{IOScin >> n;for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)cin >> w[i][j];memset(f, 0x3f, sizeof f);f[1][0] = 0;for(int i = 0; i < 1 << n; i ++){for(int j = 0; j < n; j ++)//到第j位 {if(i >> j & 1){int t = i - (1 << j);//去掉第j位 for(int k = 0; k < n; k ++)//从k转移 {if(t >> k & 1){f[i][j] = min(f[i][j], f[t][k] + w[k][j]);}}}}}cout << f[(1 << n) - 1][n - 1];return 0;
} 小国王
在 n×n 的棋盘上放 k 个国王,国王可攻击相邻的 8 个格子,求使它们无法互相攻击的方案总数。
输入格式
共一行,包含两个整数 n 和 k。
输出格式
共一行,表示方案总数,若不能够放置则输出00。
数据范围
1≤n≤10,
0≤k≤n^2
输入样例:
3 2
输出样例:
16f[i][j][k]表示前i层,第i层状态为k,摆了j个国王
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 12, M = 1 << 10, K = 110;int n, k;
ll f[N][K][M];
vector<int> state;
vector<int> head[M];
bool st[M];
int cnt[M];bool check(int x)
{for(int i = 0; i < n; i ++){if(x >> i & 1 && x >> i + 1 & 1)return false;}return true;
}int count(int x)
{int res = 0;while(x){if(x & 1)res ++;x >>= 1;}return res;
}int main()
{IOScin >> n >> k;for(int i = 0; i < 1 << n; i ++){if(check(i)){state.push_back(i);st[i] = true;cnt[i] = count(i);}}for(auto a : state){for(auto b : state){if((a & b) == 0 && st[a | b]){head[a].push_back(b);}}}f[0][0][0] = 1;for(int i = 1; i <= n + 1; i ++)//10{for(int j = 0; j <= k; j ++)//100{for(auto a : state)//1000{for(auto b : head[a])//1000{if(j >= cnt[a])f[i][j][a] += f[i - 1][j - cnt[a]][b];}}}}cout << f[n + 1][k][0];return 0;
}玉米田
农夫约翰的土地由 M×N个小方格组成,现在他要在土地里种植玉米。
非常遗憾,部分土地是不育的,无法种植。
而且,相邻的土地不能同时种植玉米,也就是说种植玉米的所有方格之间都不会有公共边缘。
现在给定土地的大小,请你求出共有多少种种植方法。
土地上什么都不种也算一种方法。
输入格式
第 11 行包含两个整数 M 和 N。
第 2..M+1 行:每行包含 N 个整数 0 或 1,用来描述整个土地的状况,1 表示该块土地肥沃,0 表示该块土地不育。
输出格式
输出总种植方法对 108108 取模后的值。
数据范围
1≤M,N≤12
输入样例:
2 3
1 1 1
0 1 0
输出样例:
9和上一题几乎一模一样
没了个数的限制,更简单一点
只是多了一个肥沃土地的限制,dp过程中判断即可
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 14, M = 1 << 12, mod = 100000000;int n, m;
int f[N][M];
vector<int> state, head[M];
bool st[M];
int g[N];bool check(int x)
{for(int i = 0; i < m; i ++){if(x >> i & 1 && x >> i + 1 & 1){return false;}}return true;
}int main()
{IOScin >> n >> m;for(int i = 1; i <= n; i ++){for(int j = 0; j < m; j ++){int x;cin >> x;g[i] += !x << j;}}for(int i = 0; i < 1 << m; i ++){if(check(i)){state.push_back(i);st[i] = true;}}for(auto a : state){for(auto b : state){if((a & b) == 0){head[a].push_back(b); }}}f[0][0] = 1;for(int i = 1; i <= n + 1; i ++){for(auto A : state){for(auto B : head[A]){ if(g[i] & A)continue;if(g[i - 1] & B)continue;//这两条语句任意保留一条都能过,只保留第一条是保证当前合法才转移,当前不合法就没有值//只保留第二条是保证上一行状态合法,只从合法状态转移过来,不合法虽然有值但不会被转移f[i][A] = (f[i][A] + f[i - 1][B]) % mod;}}}cout << f[n + 1][0];return 0;
}炮兵阵地
司令部的将军们打算在 N×M的网格地图上部署他们的炮兵部队。
一个 N×M的地图由 N行 M列组成,地图的每一格可能是山地(用 H 表示),也可能是平原(用 P 表示),如下图。
在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:

如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。
图上其它白色网格均攻击不到。
从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入格式
第一行包含两个由空格分割开的正整数,分别表示 N 和 M;
接下来的 N 行,每一行含有连续的 M 个字符(P 或者 H),中间没有空格。按顺序表示地图中每一行的数据。
输出格式
仅一行,包含一个整数 K,表示最多能摆放的炮兵部队的数量。
数据范围
N≤100,M≤10
输入样例:
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出样例:
6f[i][j][j]表示第i行,第i-1行状态为j,第i行状态为k, 状态表示为最大个数。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 110, M = 1 << 10;int n, m;
int g[N];
vector<int> state;
int f[2][M][M];
int cnt[M];bool check(int x)
{for(int i = 0; i < m; i ++){if(x >> i & 1 && (x >> i + 1 & 1 || x >> i + 2 & 1)){return false;}}return true;
}int count(int x)
{int res = 0;while(x){if(x & 1)res ++;x >>= 1;}return res;
}int main()
{IOScin >> n >> m;for(int i = 1; i <= n; i ++){for(int j = 0; j < m; j ++){char c;cin >> c;if(c == 'H')g[i] += 1 << j;}}for(int i = 0; i < 1 << m; i ++){if(check(i)){state.push_back(i);cnt[i] = count(i);}}for(int i = 1; i <= n + 2; i ++){for(auto a : state)//i - 2{for(auto b : state)//i - 1{for(auto c : state)//i{if(a & b | a & c | b & c)continue;if(c & g[i] | b & g[i - 1])continue;//和上题一样判断当前状态合法才转移f[i & 1][b][c] = max(f[i & 1][b][c], f[i - 1 & 1][a][b] + cnt[c]);}}}}cout << f[n + 2 & 1][0][0];return 0;
}愤怒的小鸟
Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于 (0,0) 处,每次 Kiana 可以用它向第一象限发射一只红色的小鸟, 小鸟们的飞行轨迹均为形如 y=ax2+bx 的曲线,其中 a,b 是 Kiana 指定的参数,且必须满足 a<0。
当小鸟落回地面(即 x 轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有 n 只绿色的小猪,其中第 i 只小猪所在的坐标为 (xi,yi)。
如果某只小鸟的飞行轨迹经过了 (xi, yi),那么第 i 只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过 (xi, yi),那么这只小鸟飞行的全过程就不会对第 i 只小猪产生任何影响。
例如,若两只小猪分别位于 (1,3) 和 (3,3),Kiana 可以选择发射一只飞行轨迹为 y=−x2+4x 的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对 Kiana 来说都很难,所以 Kiana 还输入了一些神秘的指令,使得自己能更轻松地完成这个这个游戏。
这些指令将在输入格式中详述。
假设这款游戏一共有 T个关卡,现在 Kiana 想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。
由于她不会算,所以希望由你告诉她。
注意:本题除 NOIP 原数据外,还包含加强数据。
输入格式
第一行包含一个正整数 T,表示游戏的关卡总数。
下面依次输入这 T 个关卡的信息。
每个关卡第一行包含两个非负整数 n,m,分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。
接下来的 n 行中,第 i 行包含两个正实数 (xi,yi),表示第 i 只小猪坐标为 (xi,yi),数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果 m=0,表示 Kiana 输入了一个没有任何作用的指令。
如果 m=1,则这个关卡将会满足:至多用 ⌈n/3+1⌉ 只小鸟即可消灭所有小猪。
如果 m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少 ⌊n/3⌋ 只小猪。
保证 1≤n≤18,0≤m≤2,0<xi,yi<10,输入中的实数均保留到小数点后两位。
上文中,符号 ⌈c⌉ 和 ⌊c⌋ 分别表示对 c 向上取整和向下取整,例如 :⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。
输出格式
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量。
数据范围

输入样例:
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
输出样例:
1
1首先m没用
爆搜的思想是传进来一个状态,找到没被覆盖的一个点,枚举能覆盖这个点的抛物线,再搜新状态
这里状压是对爆搜的优化
path[i][j]表示经过i、j两点的抛物线经过了哪些点
f[i]表示爆搜传进来的状态返回的值
对dp过程中只搜一个点而不是搜所有未被覆盖的点的解释:
四个点,如果最优解是选12和34,如果先选12,会先更新成1100,走到1100时再更新成1111,如果先选34,会先更新成0011,走到0011时再更新成1111,更新的顺序与结果无关,不管选哪个点都不会影响状态的遍历
而且一定是由小值更新大值的
这样复杂度会在原来的基础上乘以一个
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;
typedef pair<double, double> PDD;const int N = 18, M = 1 << 18;
const double eps = 1e-6;int n, m;
int f[M];
int path[N][N];//i j两个点之间经过哪些点
PDD dot[N];int cmp(double x, double y)
{if(fabs(x - y) < eps)return 0;if(x < y)return -1;return 1;
}void solve()
{cin >> n >> m;memset(path, 0, sizeof path);memset(f, 0x3f, sizeof f);f[0] = 0;for(int i = 0; i < n; i ++){cin >> dot[i].first >> dot[i].second;}//处理pathfor(int i = 0; i < n; i ++){path[i][i] = 1 << i;for(int j = 0; j < n; j ++){double x1 = dot[i].first, y1 = dot[i].second;double x2 = dot[j].first, y2 = dot[j].second;if(!cmp(x1, x2))continue;//不能横坐标相等 double a = (y1 / x1 - y2 / x2) / (x1 - x2);double b = y1 / x1 - a * x1;if(a >= 0)continue;//抛物线要开口向下 int state = 0;for(int k = 0; k < n; k ++){double x = dot[k].first, y = dot[k].second;if(!cmp(a * x * x + b * x, y)){state += 1 << k;}} path[i][j] = state;}} for(int i = 0; i + 1 < 1 << n; i ++){int x = -1;for(int j = 0; j < n; j ++){if(!(i >> j & 1)){x = j;break;}}for(int j = 0; j < n; j ++){f[i | path[x][j]] = min(f[i | path[x][j]], f[i] + 1);}}cout << f[(1 << n) - 1] << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}宝藏
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 n 个深埋在地下的宝藏屋,也给出了这 n 个宝藏屋之间可供开发的 m 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。
但是,每个宝藏屋距离地面都很远,也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。
已经开凿出的道路可以任意通行不消耗代价。
每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。
另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏屋之间的道路无需再开发。
新开发一条道路的代价是:
这条道路的长度 ×× 从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋)。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代价最小,并输出这个最小值。
输入格式
第一行两个用空格分离的正整数 n 和 m,代表宝藏屋的个数和道路数。
接下来 m 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏屋的编号(编号为 1∼n),和这条道路的长度 v。
输出格式
输出共一行,一个正整数,表示最小的总代价。
数据范围
1≤n≤12,
0≤m≤1000,
v≤5∗1e5
输入样例:
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1
输出样例:
4朴素dp有三维dp[i][j][k],第一维是整体的状态(有哪些点),第二维是最后一层的状态,第三维是倒数第二层的状态。但这样时间复杂度和空间复杂度过于爆炸,不能这样。
最后一层只能连向最后一层的限制我们可以换成最后一层可以连上上面任意一层(乘的那个层数不变),设前者状态为A,后者状态为B
B能取到的点范围大于A,所以能去到的最小值也会<=A,所以最终结果min(A)>=min(B)
B最后的结果肯定是一颗树的形式,以下图为例,设最小的形式是这个,假设3能取到的最小的点不在倒数第二层而是在第一层(也就是1),层数k * 路长d,d会变小,乘积也会变小,但如果3接到第二层,就会变成 (k-1)*更小的那个d ,乘积进一步变小,说明这反而就不是最小值了,就矛盾了,所以假设不成立,最小的点就在倒数第二层。而这个最终的状态是符合A的,B的最小值在A之内,得证min(A) <= min(B);
min(A)>=min(B)的同时min(A)<=min(B),证得min(A) = min(B)。
但只是计算最小值可以这样。
说得简单点就是,emm,还是以上图为例,比如3最合适的是连1,应当连在第二层,但现在连在了第三层,距离乘了2,如果连到第二层的话会乘1,这个乘1绝对是符合A状态的,乘2虽然不符合A状态,但他的值绝对是大于等于那个乘1的,两种情况都会枚举到,所以无所谓,只要包含了那个最小值就行。怎么说呢,就是那种散弹枪开一百枪,有一枪打得中就ok
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 12, M = 1 << 12, INF = 0x3f3f3f3f;int n, m;
int f[M][N];//整体状态为i,层数为j 第0层也算一层
int d[N][N], g[N][M];//点i到状态j的最短距离 int main()
{IOScin >> n >> m;memset(d, 0x3f, sizeof d);for(int i = 0; i < m; i ++){int a, b, c;cin >> a >> b >> c;a --, b --;d[a][b] = d[b][a] = min(d[a][b], c);}memset(g, 0x3f, sizeof g);for(int i = 0; i < n; i ++){for(int j = 1; j < 1 << n; j ++){for(int k = 0; k < n; k ++){if(j >> k & 1){g[i][j] = min(g[i][j], d[i][k]);}}}}memset(f, 0x3f, sizeof f);for(int i = 0; i < n; i ++){f[1 << i][0] = 0;}for(int i = 1; i < 1 << n; i ++){for(int j = i - 1 & i; j; j = j - 1 & i)//枚举i的子集 {int r = i ^ j, cost = 0;for(int k = 0; k < n; k ++){if(j >> k & 1){cost += g[k][r];if(cost >= INF)break;}}if(cost >= INF)continue;for(int k = 1; k < n; k ++){if((ll)cost * k >= INF)break;f[i][k] = min(f[i][k], f[r][k - 1] + cost * k);}}}int ans = INF;for(int i = 0; i < n; i ++){ans = min(ans, f[(1 << n) - 1][i]);}cout << ans;return 0;
}相关文章:

状态压缩 笔记
棋盘式的f[i][j]中表示状态的j可以是状态本身也可以是在合法状态state中的下标 用状态本身比较方便,用下标比较省空间 用下标的话可以开id[M]数组记录一下 蒙德里安的梦想 求把 NM的棋盘分割成若干个 12的长方形,有多少种方案。 例如当 N2࿰…...
Java 数据结构篇-实现二叉搜索树的核心方法
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 二叉搜索树的概述 2.0 二叉搜索树的成员变量及其构造方法 3.0 实现二叉树的核心接口 3.1 实现二叉搜索树 - 获取值 get(int key) 3.2 实现二叉搜索树 - 获取最小…...
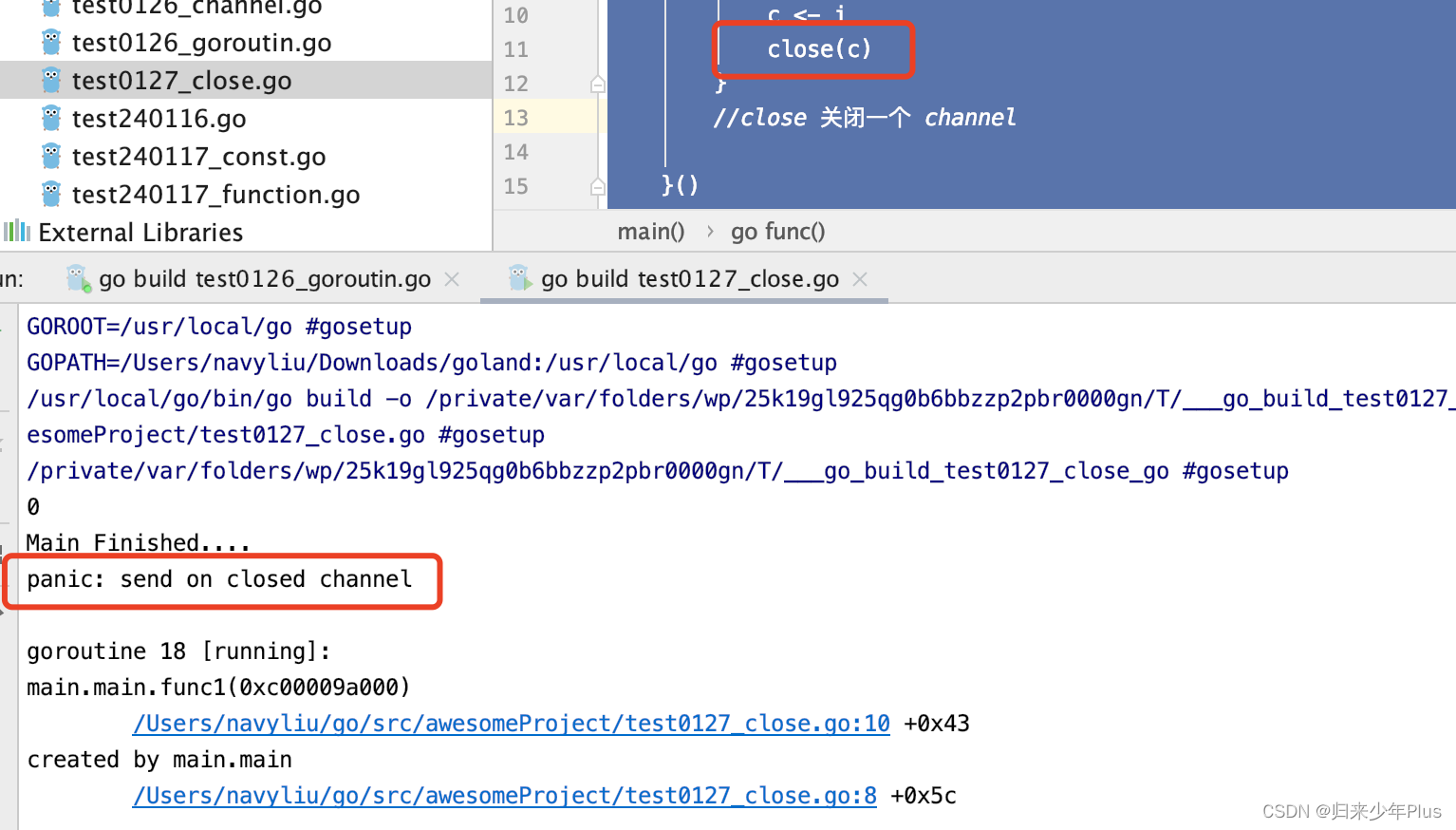
go语言(二十一)---- channel的关闭
channel不像文件一样需要经常去关闭,只有当你确实没有任何发送数据了,或者你想显示的结束range循环之类的,才去关闭channel。关闭channel后,无法向channel再发送数据,(引发pannic错误后,导致接收…...
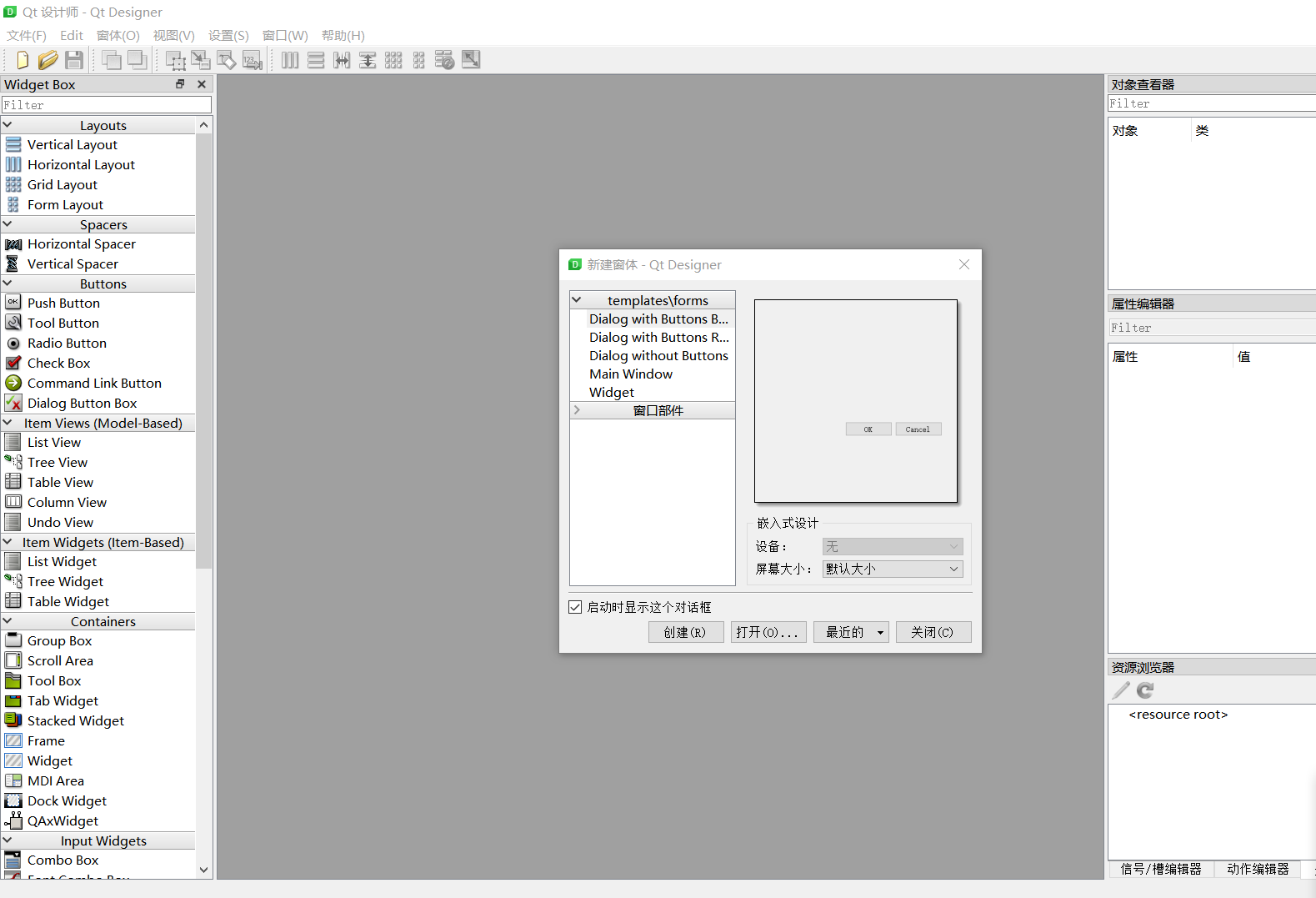
【PyQt】01-PyQt下载
文章目录 前言静态库 一、PyQt是什么?二、安装1.Windows环境下安装安装PyQt5Designer 2.Liunx环境下安装 总结 前言 拜吾师 PyQt5 快速入门 静态库 补充一点知识: Windows: .lib Linux: .a .so(动态库) 简单描述PyQt就是python调用C的Qt文…...

不一样的味觉体验:精酿啤酒与烤肉的绝妙搭配
在繁华的都市生活中,人们总是在寻找那份与众不同的味觉享受。当夏日的微风轻轻拂过,你是否想过,与三五好友围坐在一起,拿着Fendi Club啤酒与烤肉的绝妙搭配,畅谈生活点滴,感受那份惬意与自在? F…...

linux系统ansible的jiaja2的语法和简单剧本编写
jianja2语法和简单剧本 jinja2语法Jinja default()设定if语句for语句 ansiblejiaja2的使用ansible目录结构:tasks目录下文件内容:nginx模板文件ansible变量文件ansible主playbook文件测试并执行:查看检测执行结果 剧本编写安装apache安装mysq…...

Three.js PBR 物理渲染
详解 Three.js PBR 物理渲染 Three.js 是一个流行的基于 WebGL 的 JavaScript 库,专门用于创建和运行三维动画和游戏。其中很关键的一部分是物理渲染(PBR)。本文将深入探讨 Three.js 的 PBR 渲染,并为初学者提供实用的指导。 什…...
POSIX(包含程序的可移植性) -- 详解
1. 什么是 POSIX 参考链接–知乎 POSIX 标准包含了进程管理、文件管理、网络通信、线程和同步、信号处理等方面的功能。 这些接口定义了函数、数据类型和常量等,为开发者提供了一个可移植的方法来与操作系统进行交互。 2. 谁遵守这个标准 遵守 POSIX 标准的主要是…...
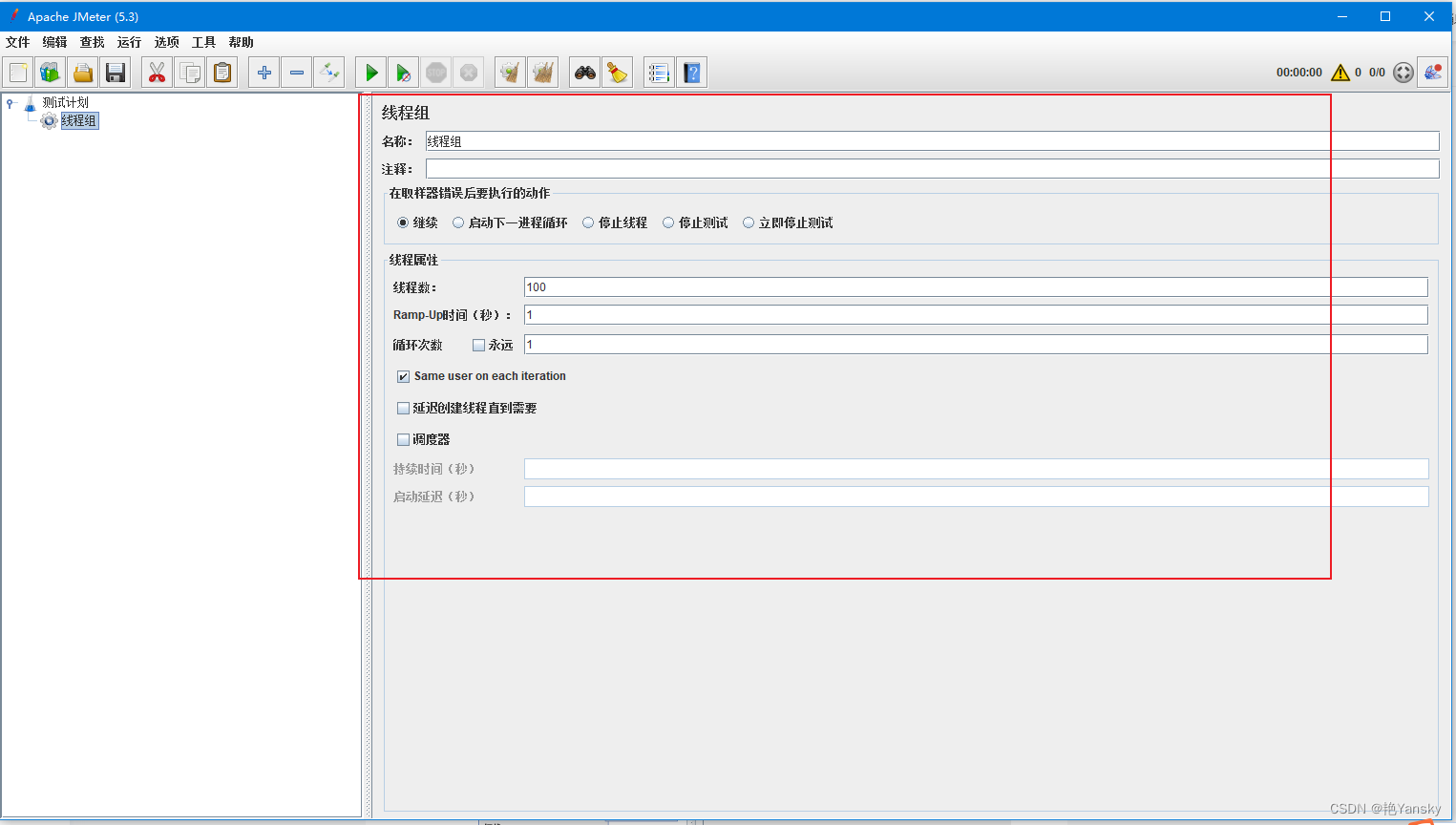
Jmeter学习系列之五:基础线程组(Thread Group)
前言 线程组是一系列线程的集合,每一个线程代表着一个正在使用应用程序的用户。在 jmeter 中,每个线程意味着模拟一个真实用户向服务器发起请求。 在 jmeter 中,线程组组件运行用户设置线程数量、初始化方式等等配置。 例如,如果你设置线程数为 100,那么 jmeter 将创建…...

Android 双卡适配 subId 相关方法
业务场景 双卡设备进行网络等业务时,需要正确操作对应的卡。 执行卡业务和主要是使用subId和 PhoneId/SlotId进行区分隔离。 代码举例 初始化subId //初始化subId private int mSubId SubscriptionManager.INVALID_SUBSCRIPTION_ID;//1、通过intent传值&#x…...
使用Logstash将MySQL中的数据同步至Elasticsearch
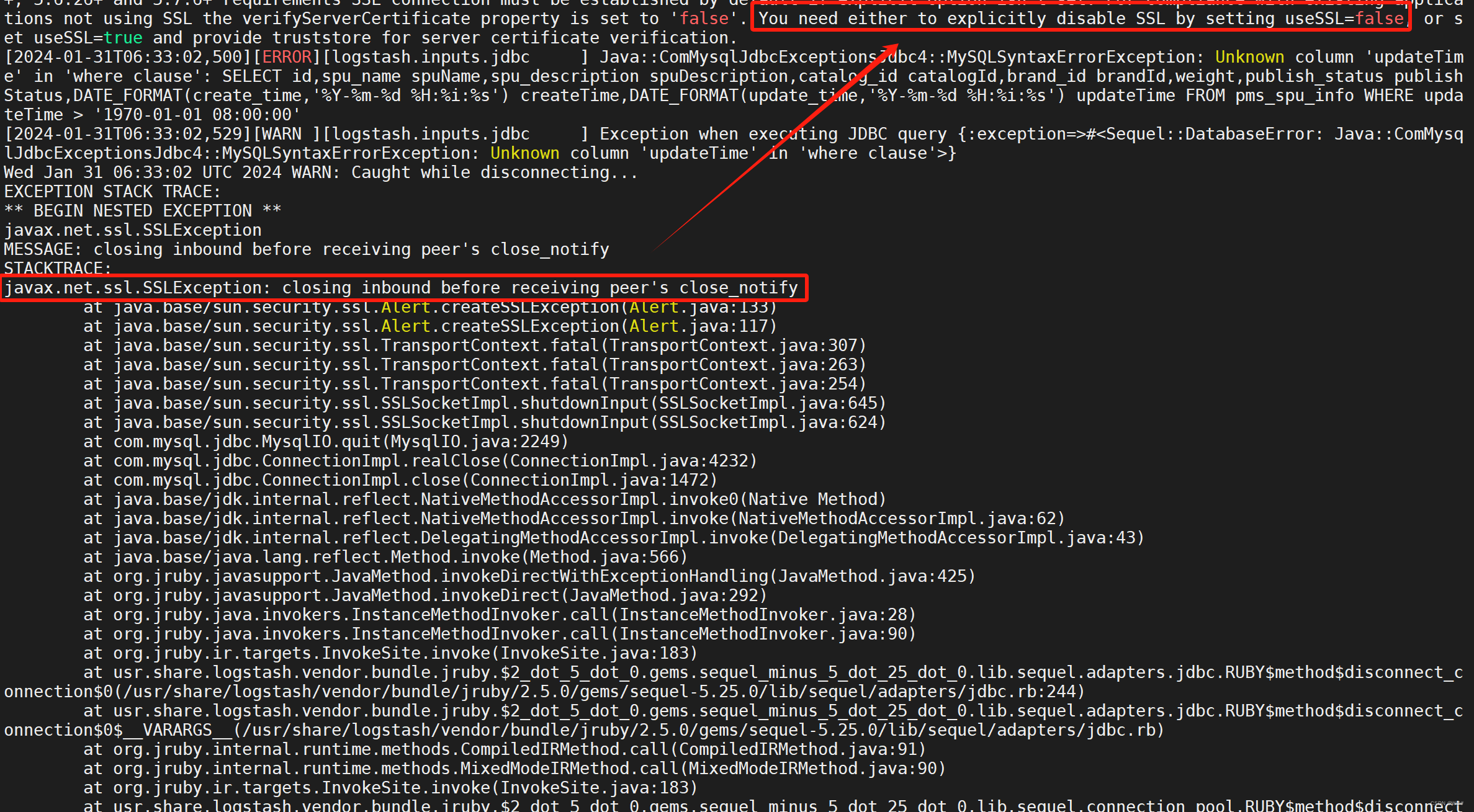
目录 1 使用docker安装ELK 1.1 安装Elasticsearch 1.2 安装Kibana 1.3 安装Logstash 2 数据同步 2.1 准备MySQL表和数据 2.2 运行Logstash 2.3 测试 3 Logstash报错(踩坑)记录 3.1 记录一 3.1.1 报错信息 3.1.2 报错原因 3.1.3 解决方案 3.2 记录二 3.2.1 报错信…...
 更新)
米贸搜|Facebook公共主页反馈分数(ACE) 更新
前段时间Meta改进了公共主页反馈分数的仪表板,发现有部分广告主似乎没有接受到这条动态,今天为大家整理出更新内容,方便各位广告主了解学习! Meta重新设计了公共主页反馈分数仪表板,以便广告主能更轻松地了解总体反馈…...

代码随想录算法训练营第三十七天| 738.单调递增的数字、968.监控二叉树
738.单调递增的数字 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 解题思路:一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然…...
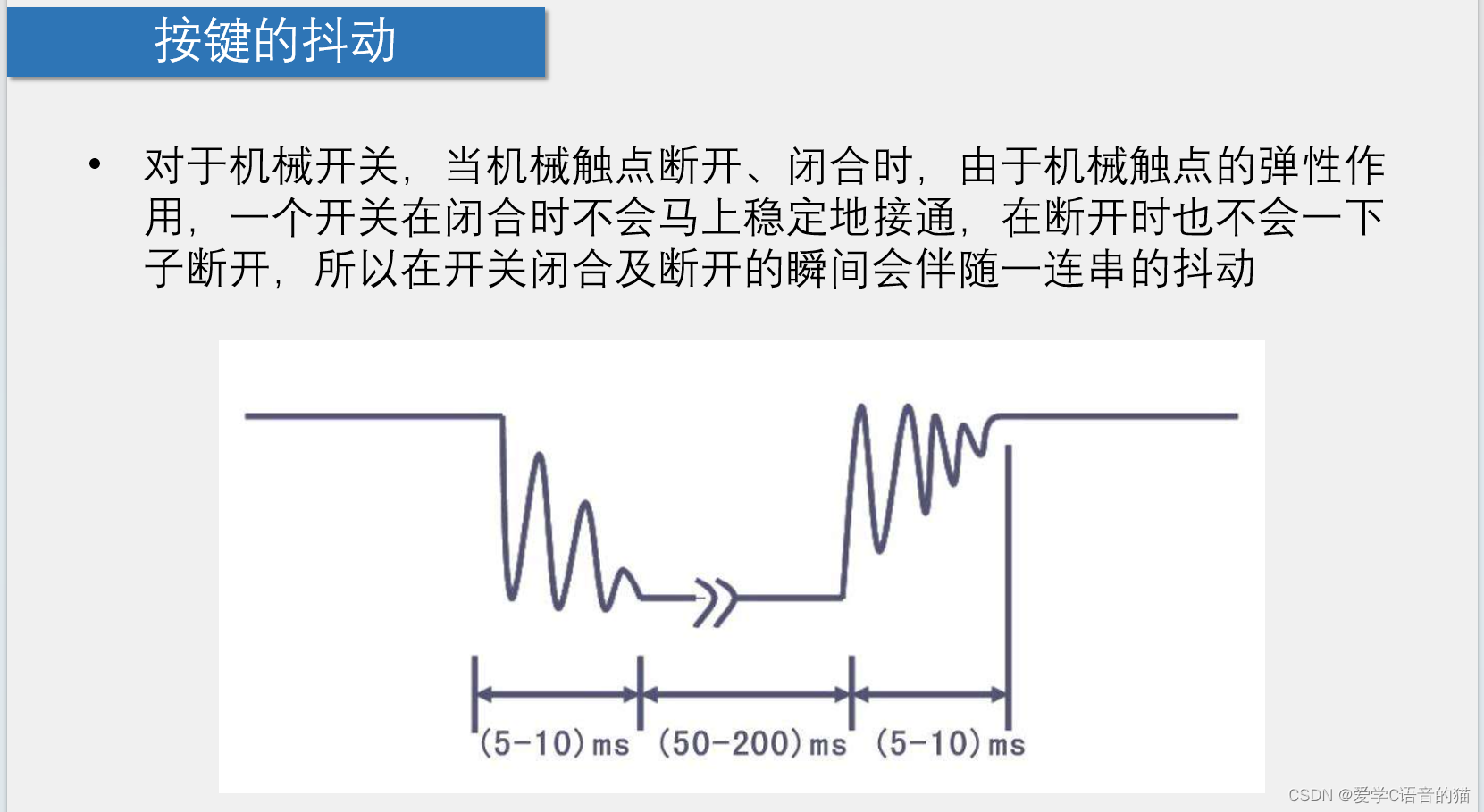
51单片机编程应用(C语言):独立按键
目录 1.独立按键介绍 2.独立按键控制LED亮灭 1.1按下时LED亮,松手LED灭(按一次执行亮灭) 1.2首先按下时无操作,松手时LED亮(再按下无操作,所以LED亮),松手LED灭(松手时…...
小程序定制开发前,应该考虑些什么?
引言 在移动互联网时代,小程序已经成为许多企业和个人推广业务、提供服务的理想平台。然而,在进行小程序定制开发之前,开发者和业务方需要细致入微地考虑一系列关键因素,以确保最终的小程序既能满足用户需求,又能够顺…...
2024/2/1学习记录
echarts 为柱条添加背景色: 若想设置折线图的点的样式,设置 series.itemStyle 指定填充颜色就好了,设置线的样式设置 lineStyle 就好了。 在折线图中倘若要设置空数据,用 - 表示即可,这对于其他系列的数据也是 适用的…...

10个React状态管理库推荐
本文将为您推荐十款实用的React状态管理库,帮助您打造出高效、可维护的前端应用。让我们一起看看这些库的魅力所在! 在前端开发中,状态管理是至关重要的一环。React作为一款流行的前端框架,其强大的状态管理功能备受开发者青睐。…...

从0开始写android
系列文章目录 文章目录 一、 从0开始实现 onCreate 的setContentView二、 从0 开始实现 onMeasure三、 从0 开始实现 onLayout四、 从0 开始实现 onDraw总结 前言 接上文,测量完View树的每个节点View的宽和高后,开始布局。 一、ViewRootImpl 的调用栈…...
使用pygame建立一个简单的使用键盘方向键移动的方块小游戏
import pygame import sys# 初始化pygame pygame.init()# 设置窗口大小 screen_size (640, 480) # 创建窗口 screen pygame.display.set_mode(screen_size) # 设置窗口标题 pygame.display.set_caption("使用键盘方向键移动的方块的简单小游戏")# 设置颜色 bg_colo…...

从零开始:CentOS系统下搭建DNS服务器的详细教程
前言 如果你希望在CentOS系统上建立自己的DNS服务器,那么这篇文章绝对是你不容错过的宝藏指南。我们提供了详尽的步骤和实用技巧,让你能够轻松完成搭建过程。从安装必要的软件到配置区域文件,我们都将一一为你呈现。无论你的身份是运维人员,还是程序员,抑或是对网络基础设…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
