计算机图形学 实验
题目要求
1.1 实验一:图元的生成:直线、圆椭区域填充
你需要完成基本的图元生成算法,包括直线和椭圆。
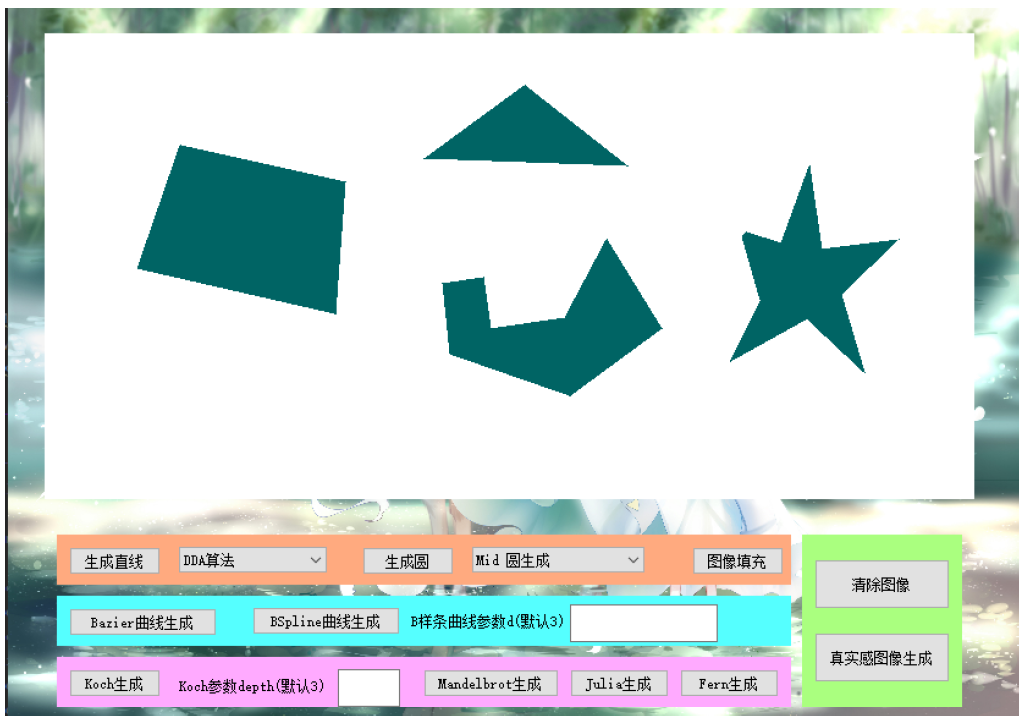
在区域填充中,要求你对一个封闭图形进行填充。你需要绘制一个封
闭图形(例如多边形),并选择一种算法进行区域填充。
你的作品应当有一定的交互功能,例如,通过鼠标确定控制点来获得
以上图形。
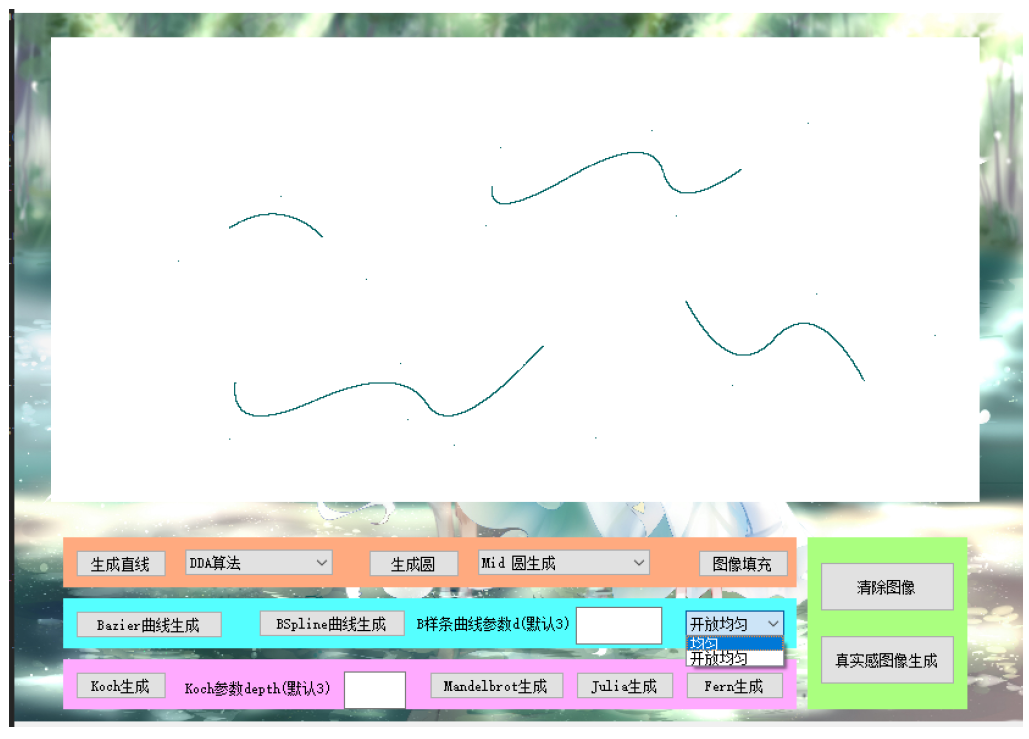
1.2 实验二:样条曲线的生成: Bezier Bezier 曲线、B-样条
曲线的生成:
你需要完成这两种曲线的生成。
对于桂栭样条曲线,统一要求实现均匀二次桂栭样条曲线。
你的作品应当有一定的交互功能,例如,通过鼠标左键确定控制点,
双击绘制曲线。
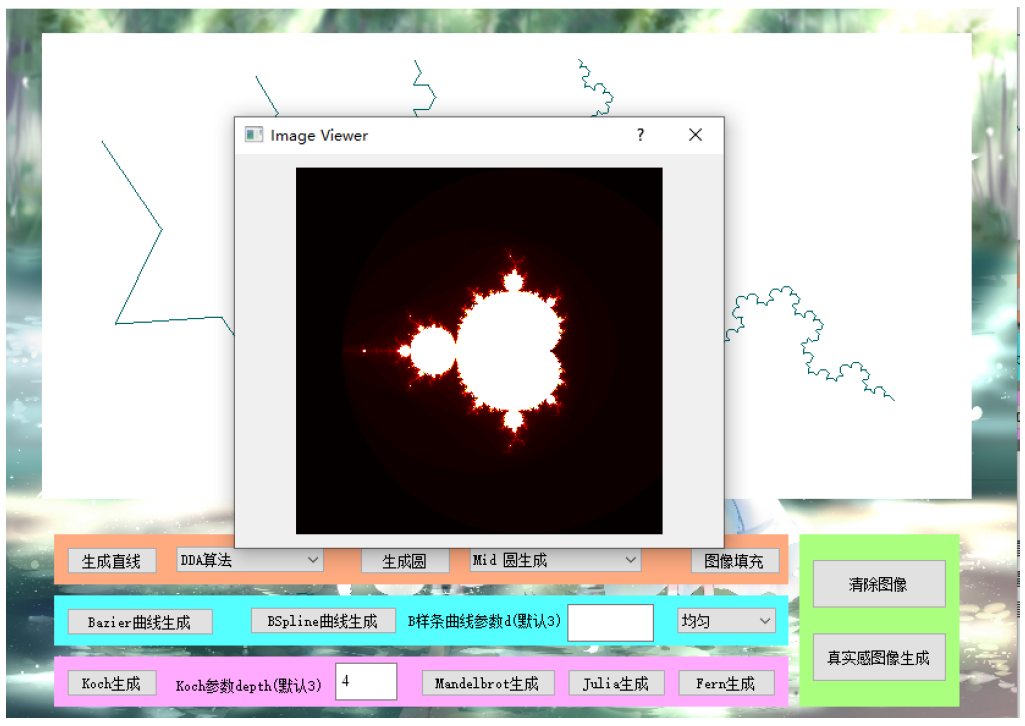
1.3 实验三:分形图的生成: Koch 曲线、Mandelbrot Mandelbrot
集和Julia 集、蕨类植物(自选两个)
以上有栴个实验内容,自选栲个做实验即可。
对于实验中涉及的参数,不做统一要求。
1.4 实验四:真实感图形的生成:显示一个具有场景,几何造型
自定义包括消隐、镜面反射纹理效果
场景自选,几何体造型自选。可以是正方体、球体等简单图形,鼓励
使用复杂一点的真实感图形。
实验效果
总体框架
使用Python编程语言,利用PyQt5库进行代码实现,只使用PyQt5的画点函数实现所有图元生成。
PyQt5是基于Qt库的Python GUI开发框架,提供了丰富的图形用户界面组件和功能,支持跨平台应用程序的开发。通过连接信号与槽,开发者可以实现事件驱动的应用程序,并可使用Qt Designer工具进行可视化界面设计。PyQt5具备多线程支持、数据库连接功能,是一个开源、跨平台的强大工具,使得开发者能够轻松创建各种桌面应用程序。
整体的软件实现分为三个部分:CG_UI、Main、Algorithm。其中CG_UI是通过PyQt5设计的实验UI界面程序,Algorithm是各种图元生成算法的实现,Main实现的是与使用者的交互,以及对图元生成算法的调用和在UI界面的绘制。整体的设计逻辑为,使用者在UI界面进行相应的坐标点选择、参数选择、算法选择过程,Main将使用者的需求处理为具体的指令,调用相应的生成算法,计算出需要在UI界面绘制的坐标点的集合,再进行最终坐标点的绘制,即完成了图元生成过程。
主程序涉及的人机交互事件主要包括按键交互事件、鼠标点击事件以及绘制事件,为了统一化的设计,我将所有试验都合并设计为了一个软件,软件界面如下图所示。

同时,我们也设计了良好的交互提示逻辑,防止软件出现bug。例如,当你在画直线时,只在画图界面中绘制了一个坐标点就点击“生成直线”时,就会弹出下图警告,而不执行相应的命令,防止出现bug。
#
实验一 图元生成
直线生成算法

圆和椭圆生成
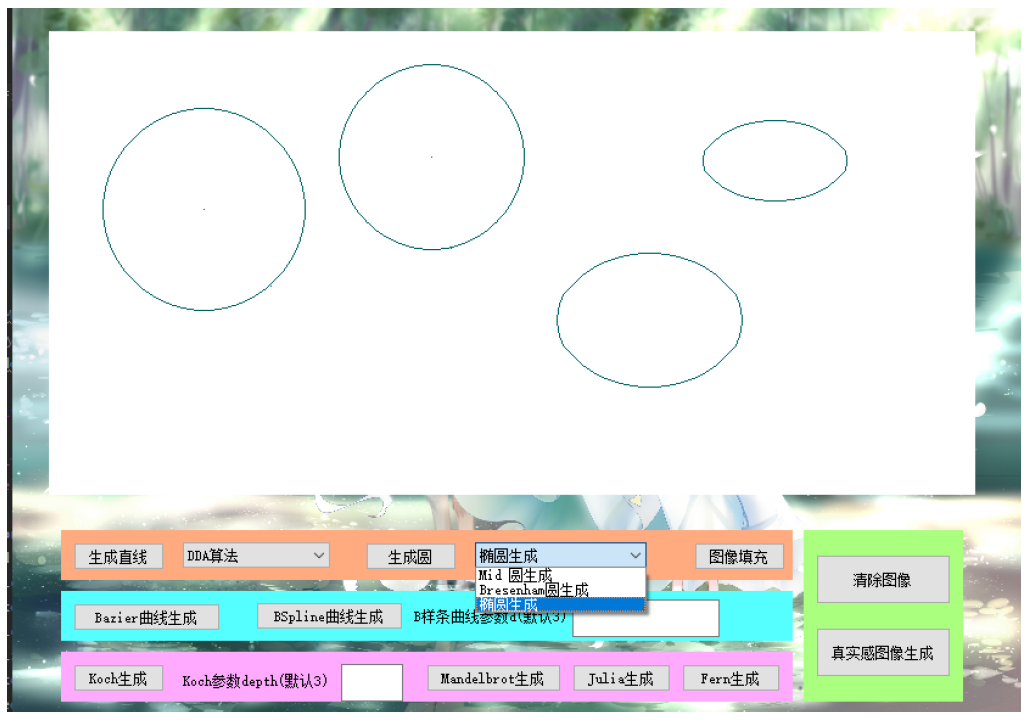
图像填充
实验二 曲线
实验三 分形图生成


实验四 真实感图形生成
代码
完整代码和软件+Q:1695251905或CSDN私信
部分代码:
class Line():def __init__(self):passdef swapPoint(self,point):""" swap start-point with end-point """temp = point[0]point[0] = point[1]point[1] = tempdef DDA(self, point, graph_points):"""DDA algorithm generate line"""dx = float(point[1][0] - point[0][0])dy = float(point[1][1] - point[0][1])m = dy / (dx+1e-9)if abs(m) <= 1:"""if abs(slope) less than 1, x_k+1 = x_k + 1, y_k+1 = y_k + m"""if point[0][0] > point[1][0]:self.swapPoint(point)k = dy / dxx = point[0][0]y = float(point[0][1])for x in range(point[0][0], point[1][0]):graph_points.append((x, int(y)))y += kelse:"""if abs(slope) more than 1, y_k+1 = y_k + 1, x_k+1 = x_k + 1/m"""if point[0][1] > point[1][1]:self.swapPoint(point)k = dx / dy # 斜率的倒数y = point[0][1]x = float(point[0][0])for y in range(point[0][1], point[1][1]):graph_points.append((int(x), y))x += kdef MidPoint(self, point, graph_points):"""MID algorithm generate line"""dx = point[1][0] - point[0][0]dy = point[1][1] - point[0][1]m = dy / dxif m > 1:"""slop > 1"""if point[0][1] > point[1][1]:self.swapPoint(point)# a = y2 - y1, b = x1 - x2b = point[1][0] - point[0][0]a = point[0][1] - point[1][1]# 判别参数p0 = a + 2 * b(扩大两倍)p = a + 2 * bd1 = 2 * (a + b)d2 = 2 * b# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while y < point[1][1]:"""y_k+1 = y_k + 1"""y += 1if p < 0:"""if p < 0, 中点在线下, x_k+1 = x_k, p_k+1 = p_k + d2"""p += d2else:"""if p > 0, 中点在线上, x_k+1 = x_k + 1, p_k+1 = p_k + d1"""p += d1x += 1graph_points.append((x, y))elif m >= 0 and m <= 1:"""斜率大于0小于1"""if point[0][0] > point[1][0]:self.swapPoint(point)# a = y2 - y1, b = x1 - x2b = point[1][0] - point[0][0]a = point[0][1] - point[1][1]# 判别参数p0 = 2 * a + b(扩大两倍)p = 2 * a + bd1 = 2 * (a + b)d2 = 2 * a# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while x < point[1][0]:"""x_k+1 = x_k + 1"""x += 1if p < 0:"""if p < 0, 中点在线下, y_k+1 = y_k + 1, p_k+1 = p_k + d1"""p += d1y += 1else:"""if p > 0, 中点在线上, y_k+1 = y_k, p_k+1 = p_k + d2"""p += d2graph_points.append((x, y))elif m < 0 and m >= -1:"""斜率小于0大于-1"""if point[0][0] > point[1][0]:self.swapPoint(point)# a = y2 - y1, b = x1 - x2b = point[1][0] - point[0][0]a = point[0][1] - point[1][1]# 判别参数p0 = 2 * a - b(扩大两倍)p = 2 * a - bd1 = 2 * (a - b)d2 = 2 * a# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while x < point[1][0]:"""x_k+1 = x_k + 1"""x += 1if p < 0:"""if p < 0, 中点在线下, y_k+1 = y_k, p_k+1 = p_k + d2"""p += d2else:"""if p > 0, 中点在线上, y_k+1 = y_k - 1, p_k+1 = p_k + d1"""p += d1y -= 1graph_points.append((x, y))else:"""斜率小于-1"""if point[0][1] < point[1][1]:self.swapPoint(point)# a = y2 - y1, b = x1 - x2b = point[1][0] - point[0][0]a = point[0][1] - point[1][1]# 判别参数p0 = 2 * b - a(扩大两倍)p = -2 * b + ad1 = -2 * (b - a)d2 = -2 * b# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while y > point[1][1]:"""y_k+1 = y_k - 1"""y -= 1if p < 0:"""if p < 0, 中点在线下, x_k+1 = x_k + 1, p_k+1 = p_k + d1"""p += d1x += 1else:"""if p > 0, 中点在线上, x_k+1 = x_k, p_k+1 = p_k + d2"""p += d2graph_points.append((x, y))def Bresenham(self, point, graph_points):"""Bresenham algorithm generate line"""dx = point[1][0] - point[0][0]dy = point[1][1] - point[0][1]m = dy / dxif m > 1:"""斜率大于1"""if point[0][1] > point[1][1]:self.swapPoint(point)delta_x = point[1][0] - point[0][0]delta_y = point[1][1] - point[0][1]# 判别参数p0 = 2 * delta_x - delta_yp = 2 * delta_x - delta_y# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while y < point[1][1]:"""y_k+1 = y_k + 1"""y += 1if p < 0:"""if p < 0, x_k+1 = x_k, p_k+1 = p_k + 2 * delta_x"""p += 2 * delta_xelse:"""if p > 0, x_k+1 = x_k + 1, p_k+1 = p_k + 2 * delta_x - 2 * delta_y"""p += 2 * delta_x - 2 * delta_yx += 1graph_points.append((x, y))elif m >= 0 and m <= 1:"""斜率大于0小于1"""if point[0][0] > point[1][0]:self.swapPoint(point)delta_x = point[1][0] - point[0][0]delta_y = point[1][1] - point[0][1]# 判别参数p0 = 2 * delta_y - delta_xp = 2 * delta_y - delta_x# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while x < point[1][0]:"""x_k+1 = x_k + 1"""x += 1if p < 0:"""if p < 0, y_k+1 = y_k, p_k+1 = p_k + 2 * delta_y"""p += 2 * delta_yelse:"""if p > 0, y_k+1 = y_k + 1, p_k+1 = p_k + 2 * delta_y - 2 * delta_x"""p += 2 * delta_y - 2 * delta_xy += 1graph_points.append((x, y))elif m < 0 and m >= -1:"""斜率小于0大于-1"""if point[0][0] > point[1][0]:self.swapPoint(point)delta_x = point[1][0] - point[0][0]delta_y = point[1][1] - point[0][1]# 判别参数p0 = 2 * delta_y + delta_xp = 2 * delta_y + delta_x# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while x < point[1][0]:"""x_k+1 = x_k + 1"""x += 1if p < 0:"""if p < 0, y_k+1 = y_k - 1, p_k+1 = p_k + 2 * delta_y - 2 * delta_x"""p += 2 * delta_y + 2 * delta_xy -= 1else:"""if p > 0, y_k+1 = y_k, p_k+1 = p_k + 2 * delta_y"""p += 2 * delta_ygraph_points.append((x, y))else:"""斜率小于-1"""if point[0][0] > point[1][0]:self.swapPoint(point)delta_x = point[0][0] - point[1][0]delta_y = point[0][1] - point[1][1]# 判别参数p0 = -2 * delta_x - delta_yp = -2 * delta_x - delta_y# 初始点x = point[0][0]y = point[0][1]graph_points.append((x, y))while y > point[1][1]:"""y_k+1 = y_k - 1"""y -= 1if p < 0:"""if p < 0, x_k+1 = x_k, p_k+1 = p_k - 2 * delta_x"""p -= 2 * delta_xelse:"""if p > 0, x_k+1 = x_k + 1, p_k+1 = p_k - 2 * delta_x - 2 * delta_y"""p -= 2 * delta_y + 2 * delta_xx += 1graph_points.append((x, y))
相关文章:

计算机图形学 实验
题目要求 1.1 实验一:图元的生成:直线、圆椭区域填充 你需要完成基本的图元生成算法,包括直线和椭圆。 在区域填充中,要求你对一个封闭图形进行填充。你需要绘制一个封 闭图形(例如多边形),并选…...

React + react-device-detect 实现设备特定的渲染
当构建响应式网页应用时,了解用户正在使用的设备类型(如手机、平板或桌面)可以帮助我们提供更优化的用户体验。本文将介绍如何在 React 项目中使用 react-device-detect 库来检测设备类型,并根据不同的设备显示不同的组件或样式。…...
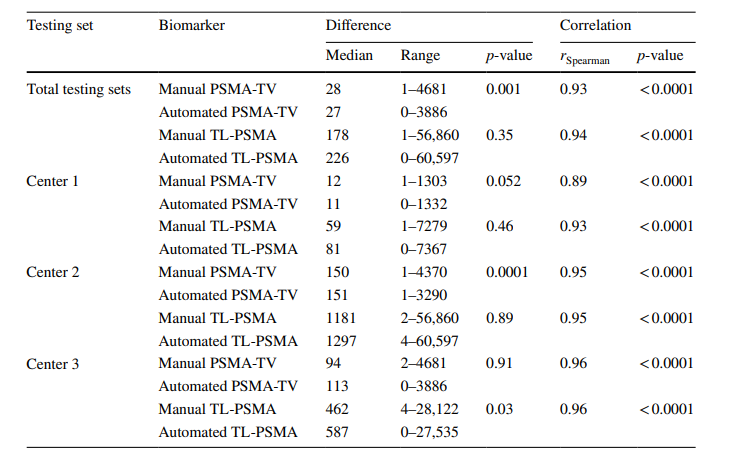
文献速递:肿瘤分割----基于卷积神经网络的系统,用于前列腺癌[68Ga]Ga-PSMA PET全身图像的全自动分割
文献速递:肿瘤分割----基于卷积神经网络的系统,用于前列腺癌[68Ga]Ga-PSMA PET全身图像的全自动分割 01 文献速递介绍 前列腺特异性膜抗原(PSMA)PET/CT成像近年来在前列腺癌检测领域中获得了显著的重视。PSMA是一种在前列腺上皮…...
2024 IC FPGA 岗位 校招面试记录
引言 各位看到这篇文章时,24届校招招聘已经渐进尾声了。 在这里记录一下自己所有面试(除了时间过短或者没啥干货的一些研究所外,如中电55所(南京),航天804所(上海))的经…...

Linux 命令 —— top
Linux 命令 —— top 相对于 ps 是选取一个时间点的进程状态,top 则可以持续检测进程运行的状态。使用方式如下: 用法: top [-d secs] | [-p pid] 选项与参数: -d secs:整个进程界面更新 secs 秒。默认是 5 5 5 秒。…...

【Docker】使用VS创建、运行、打包、部署.net core 6.0 webapi
欢迎来到《小5讲堂》,大家好,我是全栈小5。 这是《Docker容器》系列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对…...
抖音短视频矩阵营销系统源头独立开发搭建
开发背景 抖音短视频矩阵系统源码开发采用模块化设计,包括账号分析、营销活动、数据监控、自动化管理等功能。通过综合分析账号数据,快速发现账号的优势和不足,并提供全面的营销方案,以提高账号曝光率和粉丝数量。同时,…...
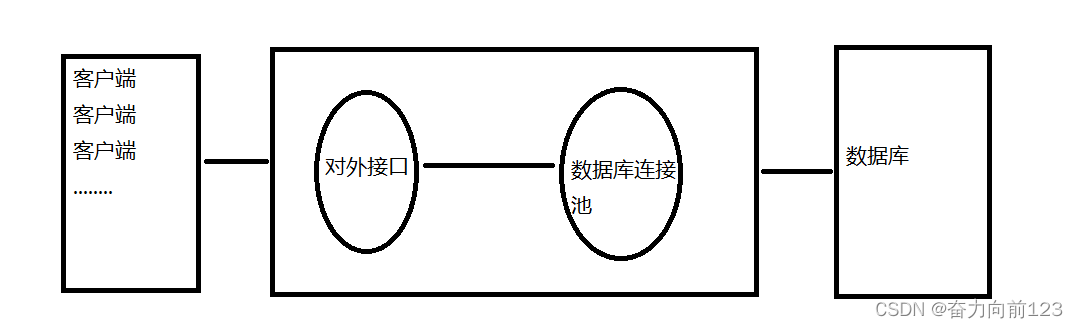
Springboot使用数据库连接池druid
springboot框架中可以使用druid进行数据库连接池,下面介绍druid在springboot中使用和参数配置介绍。 数据库连接池(Druid)是一种用于管理数据库连接的机制,其工作原理和常见使用方法如下: 原理:数据库连接…...

Springboot-前后端分离——第三篇(三层架构与控制反转(IOC)-依赖注入(DI)的学习)
本篇主要对ControllerServiceDAO三层结构以及控制反转(IOC)与DI(依赖注入)进行总结。 目录 一、三层架构: Controller/Service/DAO简介: 二、控制反转(IOC)-依赖注入(DI): 概念介绍: DOC与…...
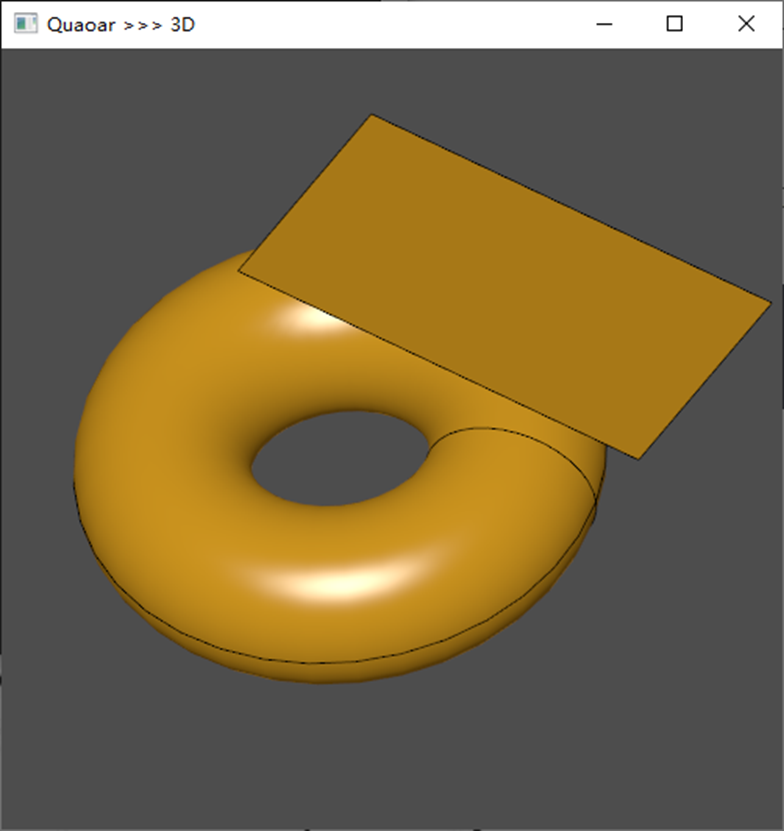
Open CASCADE学习|曲面上一点的曲率及切平面
曲率(Curvature)是一个几何学的概念,用于描述一个物体的形状在某一点上的弯曲程度。在我们日常生活中,曲率与我们的生活息息相关,如道路的弯道、建筑物的拱形结构、自然界的山脉等等。了解曲率的概念和计算方法&#x…...
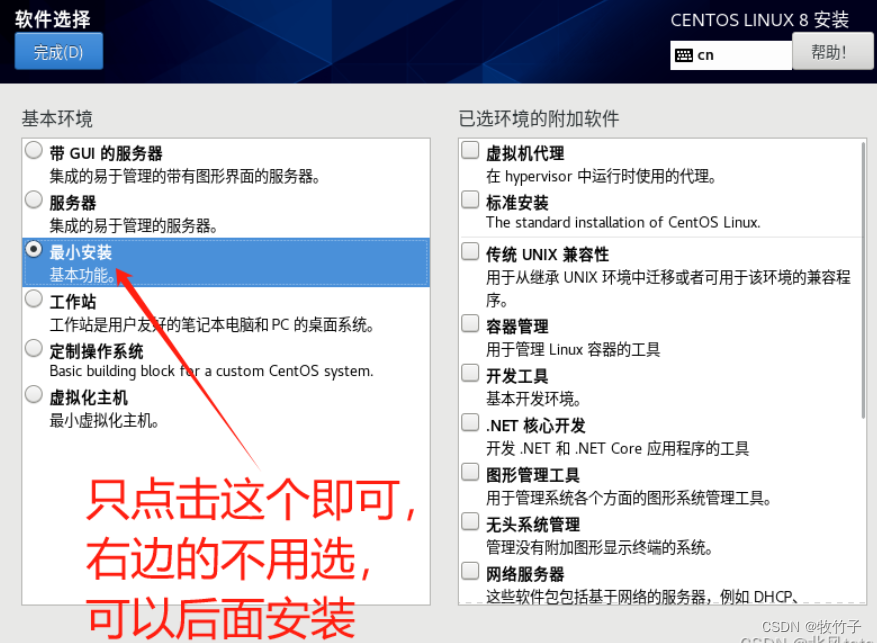
CentOS 8最小安装和网络配置
文章目录 简介下载地址VMware 17创建虚拟机最小化安装拥有的外部命令yum源有问题网络配置开启SSH Server服务关闭防火墙设置host配置JDK环境完整参考 简介 CentOS 8的IOS如果下载DVD版本至少有10G 这里我们直接选择最小安装,因此选择最小系统boot版本 CentOS-8.5.21…...

【代码随想录-链表】环形链表 II
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学习,不断总结,共同进步,活到老学到老导航 檀越剑指大厂系列:全面总结 jav…...
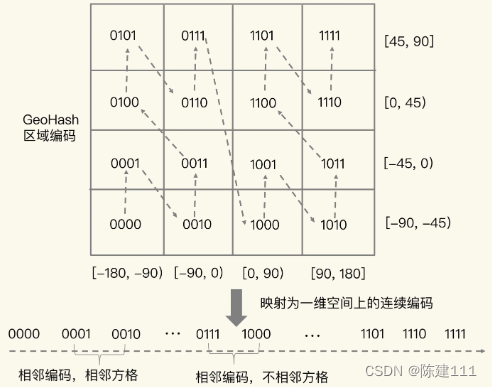
Redis核心技术与实战【学习笔记】 - 7.Redis GEO类型 - 面向 LBS 应用的数据类型
前言 前面,介绍了 Redis 的 5 大基本数据类型:String、List、Hash、Set、Sorted Set,它们可以满足绝大多数的数据存储需求,但是在面对海里数据统计时,它们的内存开销很大。所以对于一些特殊的场景,它们是无…...

银行数据仓库体系实践(17)--数据应用之营销分析
营销是每个银行业务部门重要的工作任务,银行产品市场竞争激烈,没有好的营销体系是不可能有立足之地,特别是随着互联网金融发展,金融脱媒”已越来越普遍,数字化营销方兴未艾,银行的营销体系近些年也不断发展,…...

Linux一键部署telegraf 实现Grafana Linux 图形展示
influxd2前言 influxd2 是 InfluxDB 2.x 版本的后台进程,是一个开源的时序数据库平台,用于存储、查询和可视化时间序列数据。它提供了一个强大的查询语言和 API,可以快速而轻松地处理大量的高性能时序数据。 telegraf 是一个开源的代理程序,它可以收集、处理和传输各种不…...

C/C++ C++入门
个人主页:仍有未知等待探索-CSDN博客 专题分栏:C_仍有未知等待探索的博客-CSDN博客 目录 一、C关键字 二、命名空间 1、区别 1. C语言 编辑 2. C 2、命名空间定义 3、命名空间的使用 三、C输入&输出 四、缺省参数 五、函数重载 六、引用 …...

【后端】乐观锁和悲观锁
前置知识点 锁:一种确保数据安全的机制和手段。 在多个线程修改共享变量时,我们可以对修改操作进行加锁。当多个用户修改表中的同一数据时,我们可以对该行数据进行加锁(行锁)。锁是用于控制多个操作在并发环境下按顺…...

软件工程知识梳理1-可行性研究
目的:确定问题是否值得去解决。就是用最小的代价在尽可能短的时间内确定问题是否能够解决。 可行性研究实质上是要进行一次大大压缩简化了的系统分析和设计的过程,也即是在较高层次上以较抽象的方式进行系统分析和设计的过程。 考察点:技术可…...

2024美国大学生数学建模E题财产保险的可持续模型详解思路+具体代码
2024美国大学生数学建模E题财产保险的可持续模型详解思路具体代码 前言 很快啊!啪的一下拿到题目就开始做题!简单介绍一下我自己:博主专注建模五年,参与过大大小小数十来次数学建模,理解各类模型原理以及每种模型的建…...

pytorch nearest upsample整数型tensor
在用 torch.nn.Upsample 给分割 label 上采样时报错:RuntimeError: "upsample_nearest2d_out_frame" not implemented for Long。 参考 [1-3],用 [3] 给出的实现。稍微扩展一下,支持 h、w 用不同的 scale factor,并测试…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
