算法设计与分析实验:最短路径算法
一、网络延迟时间
力扣第743题

本题采用最短路径的思想进行求解
1.1 具体思路
(1)使用邻接表表示有向图:首先,我们可以使用邻接表来表示有向图。邻接表是一种数据结构,用于表示图中顶点的相邻关系。在这个问题中,我们可以使用字典(Python 中的 defaultdict)来实现邻接表,其中键是源节点,值是一个列表,包含了从该源节点出发的边以及对应的传递时间。
(2)使用最短路径算法计算从节点 K 到其他节点的最短路径:我们可以使用 Dijkstra 算法或者 Bellman-Ford 算法来计算从节点 K 到其他所有节点的最短路径。这些算法可以帮助我们找到从节点 K 出发,到达其他节点的最短路径长度。在这个问题中,我们可以使用 Dijkstra 算法,它能够高效地处理正权重边的最短路径问题。
(3)找出最长的最短路径:最后,我们找出所有最短路径中的最大值,即找到信号传递到所有节点所需的时间。这是因为信号需要经过最长的最短路径才能传递到所有节点。如果有节点无法收到信号,我们将返回-1。
1.2 思路展示
假设我们有以下有向图和起始节点 K:
图示例:

起始节点 K = 2
对应的邻接表为:
{
2: [(1, 2), (3, 1)],
3: [(4, 1)],
1: [(3, 1), (4, 2)]
}
然后使用 Dijkstra 算法来计算从节点 2 出发到其他节点的最短路径。过程如下:
从节点 2 出发,到达节点 1 的距离为 2,到达节点 3 的距离为 1。
选择距离最短的节点 3,然后更新节点 3 相邻节点的距离:到达节点 4 的距离为 2。
最终得到的最短路径为:从节点 2 出发到节点 1 的最短路径长度为 2,到节点 3 的最短路径长度为 1,到节点 4 的最短路径长度为 2。
最长的最短路径为 2,即信号传递到所有节点所需的时间为 2。
1.3 代码实现
-
import collections import heapqdef networkDelayTime(times, n, k):# 构建邻接表表示的有向图graph = collections.defaultdict(list)for u, v, w in times:graph[u].append((v, w))# 使用 Dijkstra 算法计算最短路径pq = [(0, k)] # 优先队列,存储节点及当前距离dist = {} # 存储从节点 K 到各节点的最短路径长度while pq:d, node = heapq.heappop(pq)if node in dist:continuedist[node] = dfor nei, d2 in graph[node]:if nei not in dist:heapq.heappush(pq, (d + d2, nei))# 找出最长的最短路径,即找到信号传递到所有节点所需的时间if len(dist) == n:return max(dist.values())else:return -1# 示例输入 times = [[2, 1, 1], [2, 3, 1], [3, 4, 1]] n = 4 k = 2# 输出结果 print(networkDelayTime(times, n, k))1.4 复杂度分析
这段代码使用了Dijkstra算法来计算最短路径,下面是对其时间复杂度的分析:
构建邻接表表示的有向图:遍历times列表中的每个元素,时间复杂度为O(E),其中E为times的长度。
使用Dijkstra算法计算最短路径:最坏情况下,需要遍历所有的节点和边。每次从优先队列中弹出距离最小的节点,时间复杂度为O(logN),其中N为节点的总数。在每个节点上,需要遍历其邻居节点,时间复杂度为O(K),其中K为节点的平均邻居节点数。因此,总的时间复杂度为O((N+K)logN)。
找出最长的最短路径:遍历dist字典中的所有值,时间复杂度为O(N)。
综上所述,整体的时间复杂度为O(E + (N+K)logN + N)。空间复杂度为O(N+E),其中N为节点的总数,E为边的总数。
1.5 运行结果
# 示例输入
times = [[2, 1, 1], [2, 3, 1], [3, 4, 1]]
n = 4
k = 2
运行结果与预期一致
二、概率最大的路径
力扣第1514题

本题依旧采用最短路径的思想解决
2.1 具体思路
可以使用Dijkstra算法来解决。
首先构建无向加权图:使用字典graph来表示图,键为节点编号,值为一个列表,表示与该节点相邻的节点及对应的边权重。遍历edges和succProb两个列表,将节点和对应的边权重添加到graph中。
初始化距离列表和概率列表:使用列表dist和probs来分别存储从起点到每个节点的最短距离和成功概率。将起点的最短距离设置为1,其余节点的最短距离设置为0,起点的成功概率设置为1,其余节点的成功概率设置为0。
使用Dijkstra算法计算最短路径:使用堆优化的Dijkstra算法来计算从起点到每个节点的最短距离和成功概率。首先将起点加入优先队列pq。在每次循环中,从优先队列中弹出距离最小的节点node,遍历与该节点相邻的节点nei。如果从起点到nei的路径的成功概率乘以nei到node的边权重大于从起点到node的最短距离,并且这个概率乘以边权重大于nei节点当前的成功概率,则更新nei节点的最短距离和成功概率,并将(nei, -距离)添加到优先队列中。
返回终点的成功概率:如果终点的成功概率大于0,则返回终点的成功概率,否则返回0。
2.2 思路展示
假设给定无向加权图,其中节点0到节点3的成功概率最大。
首先,我们将这个图构建成一个字典graph,如下所示:
graph = {
0: [(1, -math.log(0.5)), (2, -math.log(0.2))],
1: [(0, -math.log(0.5)), (2, -math.log(0.5))],
2: [(0, -math.log(0.2)), (1, -math.log(0.5)), (3, -math.log(0.3))],
3: [(2, -math.log(0.3))]
}
接下来,我们初始化距离和概率列表,如下所示:
dist = [0, 0, 0, 0]
probs = [0, 0, 0, 0]
dist[0] = 1
probs[0] = 1
然后,我们使用Dijkstra算法计算最短路径。首先将起点0加入优先队列pq。在第一次循环中,从优先队列中弹出距离最小的节点0,遍历与该节点相邻的节点1和2。由于从起点到节点1的路径的成功概率乘以1到0的边权重(即-log(0.5))等于0.5,大于从起点到节点0的最短距离1,并且这个概率乘以边权重大于节点1当前的成功概率0,则更新节点1的最短距离和成功概率,并将(1, -距离)添加到优先队列中。同样的,我们也会更新节点2的最短距离和成功概率。
在第二次循环中,从优先队列中弹出距离最小的节点1,遍历与该节点相邻的节点0和2。由于从起点到节点0的路径的成功概率乘以1到0的边权重等于0.5,大于从起点到节点1的最短距离并且这个概率乘以边权重大于节点0当前的成功概率0,则更新节点0的最短距离和成功概率,并将(0, -距离)添加到优先队列中。同时,我们也会更新节点2的最短距离和成功概率。
在第三次循环中,从优先队列中弹出距离最小的节点2,遍历与该节点相邻的节点0、1和3。由于从起点到节点3的路径的成功概率乘以2到3的边权重(即-log(0.3))等于0.8,大于从起点到节点2的最短距离并且这个概率乘以边权重大于节点3当前的成功概率0,则更新节点3的最短距离和成功概率,并将(3, -距离)添加到优先队列中。我们也会更新节点0和1的最短距离和成功概率。
在最后一次循环中,从优先队列中弹出距离最小的节点3,发现它没有相邻的节点,结束Dijkstra算法的计算过程。
最后,我们返回终点3的成功概率0.25。
2.3 代码实现
import heapq
import math
from collections import defaultdictdef maxProbability(n, edges, succProb, start, end):# 构建无向带权图graph = defaultdict(list)for i in range(len(edges)):u, v = edges[i]p = succProb[i]graph[u].append((v, -math.log(p)))graph[v].append((u, -math.log(p)))# 初始化概率列表probs = [0] * nprobs[start] = 1# 使用Dijkstra算法计算最大成功概率路径pq = [(-1, start)]while pq:prob, node = heapq.heappop(pq)prob = -prob # 取相反数以便按概率从大到小排序if node == end:return probfor nei, edge_prob in graph[node]:new_prob = prob * math.exp(edge_prob)if new_prob > probs[nei]:probs[nei] = new_probheapq.heappush(pq, (-new_prob, nei))# 如果没有从起点到终点的路径,则返回0return 0# 示例测试
n = 3
edges = [[0,1],[1,2],[0,2]]
succProb = [0.5,0.5,0.2]
start = 0
end = 2
print(maxProbability(n, edges, succProb, start, end)) # 输出: 0.25succProb = [0.5,0.5,0.3]
print(maxProbability(n, edges, succProb, start, end)) # 输出: 0.3edges = [[0,1]]
succProb = [0.5]
print(maxProbability(n, edges, succProb, start, end)) # 输出: 02.4 复杂度分析
这段代码的时间复杂度为 O(ElogV),其中 E 是边数,V 是节点数。这是因为在 Dijkstra 算法中,每条边最多会被遍历一次,而堆的插入和弹出操作的时间复杂度为 O(logV),因此总时间复杂度为 O(ElogV)。
空间复杂度为 O(V),主要是用来存储概率列表和堆。
2.5 运行结果
与预期结果均保持一致
三、最小路径和
力扣第64题

本题采用动态规划的思想解决
3.1 具体思路
定义一个二维数组 dp,其大小为 m x n。其中 dp[i][j] 表示从左上角到达网格位置 (i, j) 的最小路径和。
初始化第一行和第一列的路径和,因为只能向右或向下移动,所以第一行的路径和为前一个位置的路径和加上当前位置的值,第一列的路径和同理。
对于其他位置 (i, j),可以从上方或左方移动过来,选择路径和较小的那个路径,并加上当前位置的值。
遍历整个网格,更新 dp 数组中的路径和,直到达到右下角位置 (m-1, n-1)。
返回 dp[m-1][n-1],即右下角位置的最小路径和。
3.2 思路展示
假设输入的网格为:
1 3 1
1 5 1
4 2 1
首先定义一个二维数组 dp,其大小为 m x n。其中 dp[i][j] 表示从左上角到达网格位置 (i, j) 的最小路径和。
0 0 0
0 0 0
0 0 0
然后初始化第一行和第一列的路径和,因为只能向右或向下移动,所以第一行的路径和为前一个位置的路径和加上当前位置的值,第一列的路径和同理。
1 4 5
2 0 0
6 0 0
对于其他位置 (i, j),可以从上方或左方移动过来,选择路径和较小的那个路径,并加上当前位置的值。
1 4 5
2 7 6
6 8 7
遍历整个网格,更新 dp 数组中的路径和,直到达到右下角位置 (m-1, n-1)。
最后返回 dp[m-1][n-1],即右下角位置的最小路径和。
3.3 代码实现
def minPathSum(grid):m, n = len(grid), len(grid[0])dp = [[0] * n for _ in range(m)]# 初始化第一行和第一列的路径和dp[0][0] = grid[0][0]for i in range(1, m):dp[i][0] = dp[i-1][0] + grid[i][0]for j in range(1, n):dp[0][j] = dp[0][j-1] + grid[0][j]# 动态规划更新路径和for i in range(1, m):for j in range(1, n):dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]return dp[m-1][n-1]# 示例测试
grid = [[1,3,1],[1,5,1],[4,2,1]]
print(minPathSum(grid)) # 输出: 7grid = [[1,2,3],[4,5,6]]
print(minPathSum(grid)) # 输出: 123.4 复杂度分析
这段代码的时间复杂度为 O(m*n),其中 m 和 n 分别是网格的行数和列数。这是因为代码中使用了两层嵌套的循环来遍历整个网格,并更新 dp 数组中的路径和。
空间复杂度为 O(m*n),因为创建了一个与网格大小相同的二维数组 dp,用于存储路径和。
总结起来,这段代码通过动态规划的思想,利用一个二维数组记录从左上角到达每个位置的最小路径和,最后返回右下角位置的路径和。时间和空间复杂度都是网格的大小,因此在实践中,如果网格较大,可能需要考虑优化算法或使用其他方法来减少时间和空间开销。
3.5 运行结果
# 示例测试
grid = [[1,3,1],[1,5,1],[4,2,1]]
print(minPathSum(grid)) # 输出: 7
grid = [[1,2,3],[4,5,6]]
print(minPathSum(grid)) # 输出: 12
运行结果均与预期一致
结尾语
选择大于努力!

2025-2-2
相关文章:

算法设计与分析实验:最短路径算法
一、网络延迟时间 力扣第743题 本题采用最短路径的思想进行求解 1.1 具体思路 (1)使用邻接表表示有向图:首先,我们可以使用邻接表来表示有向图。邻接表是一种数据结构,用于表示图中顶点的相邻关系。在这个问题中&am…...
共用体与枚举法,链表的学习
结构体注意事项: 1.结构体类型可以定义在main函数里面,但是此时的作用域就被限定在该函数中 2.结构体的的的定义的形式:a.先定义类型,后定义变量-----struct stu s b.定义类型的同时,定义了变量:struct…...
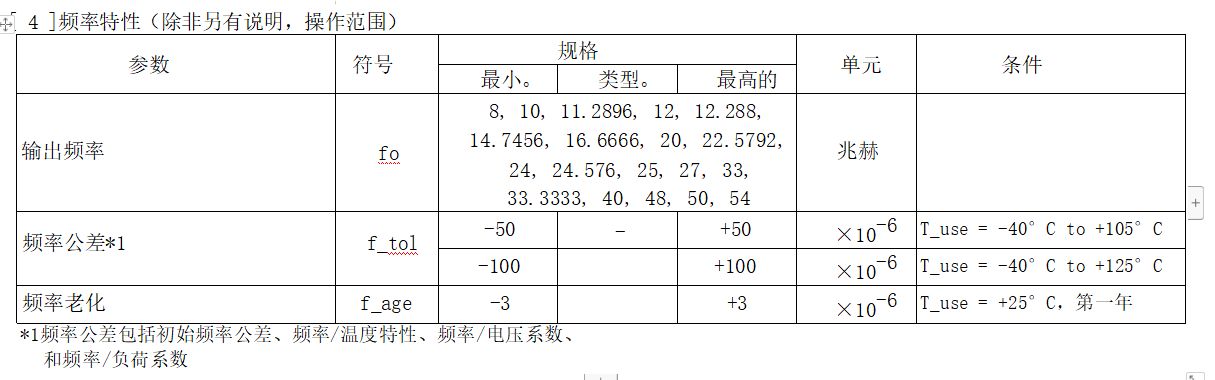
SG2520CAA汽车用晶体振荡器
爱普生SG2520CAA是简单的封装晶体振荡器(SPXO),具有CMOS输出,这款SPXO是汽车和高可靠性应用的理想选择,符合AEC-Q200标准,功耗低,工作电压范围为1.8 V ~ 3.3 V类型,宽工作温度-40℃~…...

使用pip将第三方依赖包下载到本地指定位置
pip download -d save_path packages -d:后面接下载包路径(save_path) packages:安装包名称...
C语言探索:水仙花数的奥秘与计算
摘要: 水仙花数,一种特殊的三位数,其各位数字的立方和等于该数本身。本文将详细介绍水仙花数的定义、性质,以及如何使用C语言来寻找100至999范围内的水仙花数。 目录 一、水仙花数的定义与性质 二、用C语言寻找100至999范围内的…...

2024年人工智能应用与先进制造科学国际学术会议(ICAIAAMS 2024)
2024年人工智能应用与先进制造科学国际学术会议(ICAIAAMS 2024) 2024 International Conference on Artificial Intelligence Applications and Advanced Manufacturing Science (ICAIAAMS 2024) 会议简介: 2024年人工智能应用与先进制造科学国际学术会议ÿ…...
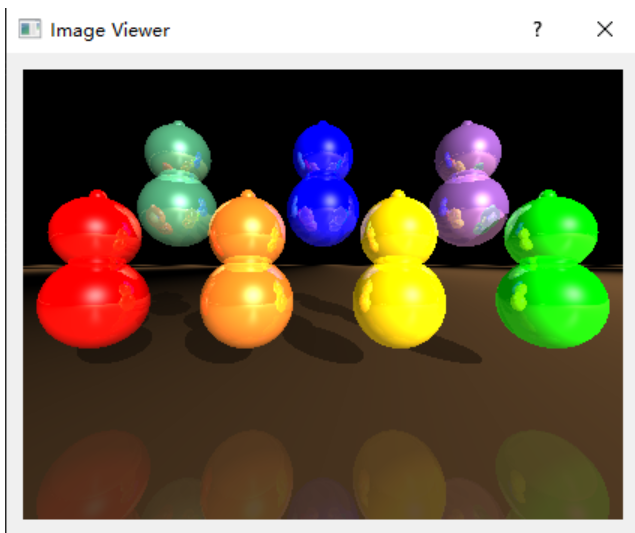
计算机图形学 实验
题目要求 1.1 实验一:图元的生成:直线、圆椭区域填充 你需要完成基本的图元生成算法,包括直线和椭圆。 在区域填充中,要求你对一个封闭图形进行填充。你需要绘制一个封 闭图形(例如多边形),并选…...

React + react-device-detect 实现设备特定的渲染
当构建响应式网页应用时,了解用户正在使用的设备类型(如手机、平板或桌面)可以帮助我们提供更优化的用户体验。本文将介绍如何在 React 项目中使用 react-device-detect 库来检测设备类型,并根据不同的设备显示不同的组件或样式。…...
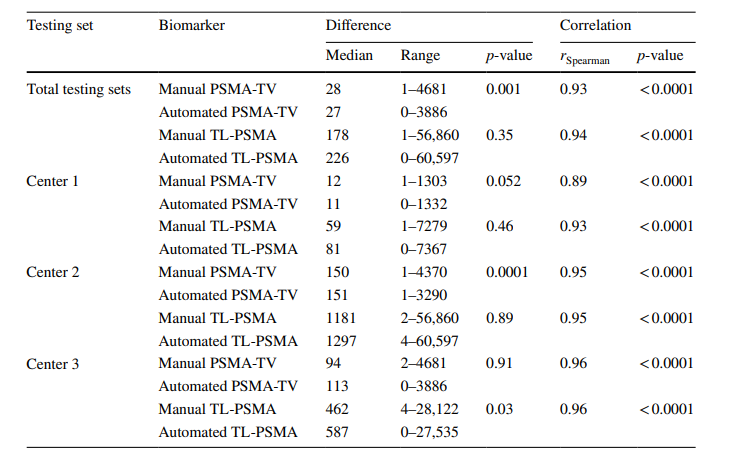
文献速递:肿瘤分割----基于卷积神经网络的系统,用于前列腺癌[68Ga]Ga-PSMA PET全身图像的全自动分割
文献速递:肿瘤分割----基于卷积神经网络的系统,用于前列腺癌[68Ga]Ga-PSMA PET全身图像的全自动分割 01 文献速递介绍 前列腺特异性膜抗原(PSMA)PET/CT成像近年来在前列腺癌检测领域中获得了显著的重视。PSMA是一种在前列腺上皮…...
2024 IC FPGA 岗位 校招面试记录
引言 各位看到这篇文章时,24届校招招聘已经渐进尾声了。 在这里记录一下自己所有面试(除了时间过短或者没啥干货的一些研究所外,如中电55所(南京),航天804所(上海))的经…...

Linux 命令 —— top
Linux 命令 —— top 相对于 ps 是选取一个时间点的进程状态,top 则可以持续检测进程运行的状态。使用方式如下: 用法: top [-d secs] | [-p pid] 选项与参数: -d secs:整个进程界面更新 secs 秒。默认是 5 5 5 秒。…...

【Docker】使用VS创建、运行、打包、部署.net core 6.0 webapi
欢迎来到《小5讲堂》,大家好,我是全栈小5。 这是《Docker容器》系列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对…...
抖音短视频矩阵营销系统源头独立开发搭建
开发背景 抖音短视频矩阵系统源码开发采用模块化设计,包括账号分析、营销活动、数据监控、自动化管理等功能。通过综合分析账号数据,快速发现账号的优势和不足,并提供全面的营销方案,以提高账号曝光率和粉丝数量。同时,…...
Springboot使用数据库连接池druid
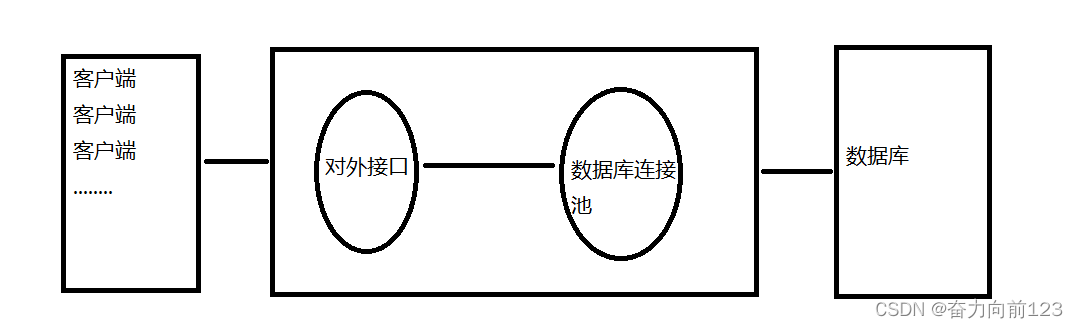
springboot框架中可以使用druid进行数据库连接池,下面介绍druid在springboot中使用和参数配置介绍。 数据库连接池(Druid)是一种用于管理数据库连接的机制,其工作原理和常见使用方法如下: 原理:数据库连接…...

Springboot-前后端分离——第三篇(三层架构与控制反转(IOC)-依赖注入(DI)的学习)
本篇主要对ControllerServiceDAO三层结构以及控制反转(IOC)与DI(依赖注入)进行总结。 目录 一、三层架构: Controller/Service/DAO简介: 二、控制反转(IOC)-依赖注入(DI): 概念介绍: DOC与…...
Open CASCADE学习|曲面上一点的曲率及切平面
曲率(Curvature)是一个几何学的概念,用于描述一个物体的形状在某一点上的弯曲程度。在我们日常生活中,曲率与我们的生活息息相关,如道路的弯道、建筑物的拱形结构、自然界的山脉等等。了解曲率的概念和计算方法&#x…...
CentOS 8最小安装和网络配置
文章目录 简介下载地址VMware 17创建虚拟机最小化安装拥有的外部命令yum源有问题网络配置开启SSH Server服务关闭防火墙设置host配置JDK环境完整参考 简介 CentOS 8的IOS如果下载DVD版本至少有10G 这里我们直接选择最小安装,因此选择最小系统boot版本 CentOS-8.5.21…...

【代码随想录-链表】环形链表 II
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学习,不断总结,共同进步,活到老学到老导航 檀越剑指大厂系列:全面总结 jav…...
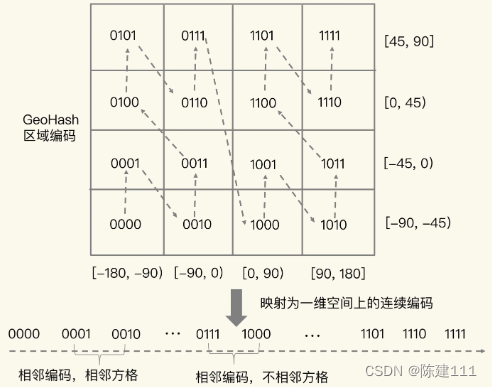
Redis核心技术与实战【学习笔记】 - 7.Redis GEO类型 - 面向 LBS 应用的数据类型
前言 前面,介绍了 Redis 的 5 大基本数据类型:String、List、Hash、Set、Sorted Set,它们可以满足绝大多数的数据存储需求,但是在面对海里数据统计时,它们的内存开销很大。所以对于一些特殊的场景,它们是无…...

银行数据仓库体系实践(17)--数据应用之营销分析
营销是每个银行业务部门重要的工作任务,银行产品市场竞争激烈,没有好的营销体系是不可能有立足之地,特别是随着互联网金融发展,金融脱媒”已越来越普遍,数字化营销方兴未艾,银行的营销体系近些年也不断发展,…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
