【刷题笔记】之二分查找(搜索插入位置。在排序数组中查找元素的第一个和最后一个位置、x的平方根、有效的完全平方数)
1. 二分查找
题目链接 704. 二分查找 - 力扣(LeetCode)
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
思路
进行二分查找的前置条件:数组有序并且数组中无重复元素
写二分查找题的代码,需要考虑清楚边界条件,比如应该是 while(left < right) 还是 where(left <= right),应该是 right = mid - 1 还是 right = mid
主要在写代码时要考虑清楚区间的范围,必须要在二分查找的过程中,根据范围保持不变量,也就是在 while 中每一次边界的处理根据区间进行操作
写二分查找,区间的定义一般有两种,左闭右闭 [left , right],左闭右开 [left , right)
写法一:左闭右闭
首先明确,我们定义的 target 是在区间 [left , right] 中,其次根据范围确定两点
while (left <= right) 这里要使用 <=,因为是左闭右闭的区间, left == right 有意义
if (nums[mid] > target) right = mid - 1,因为 nums[mid] > target,所以当前这个 nums[mid] 一定不是 target,并且是左闭右闭区间,所以缩小范围,right = mid - 1
class Solution {public int search(int[] nums, int target) {int left = 0, right = nums.length - 1;if (target < nums[left] || target > nums[right]) {return -1;}while (left <= right) {int mid = left + (right - left)/2;if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] < target) {left = mid + 1;} else {return mid;}}return -1;}
}写法二:左闭右开
首先明确,我们定义的 target 是在区间 [left , right) 中,其次根据范围确定两点
while (left < right) 这里要使用 <, left == right 没有意义,因为是左闭右开的区间
if (nums[mid] > target) right = mid ,因为 nums[mid] > target,所以当前这个 nums[mid] 一定不是 target,那么就要去左区间寻找,因为区间范围是左闭右开的,所以 right = mid,下一次查询区间不会去比较 nums[mid]
class Solution {public int search(int[] nums, int target) {int left = 0, right = nums.length;while (left < right) {int mid = left + (right - left)/2;if (nums[mid] > target) {right = mid;} else if (nums[mid] < target) {left = mid + 1;} else {return mid;}}return -1;}
}2. 搜索插入位置
题目链接:35. 搜索插入位置 - 力扣(LeetCode)
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的 升序 排列数组
-104 <= target <= 104
思路
在数组中插入目标值 target,只有这四种情况

target 在数组所有元素之前
target == 数组中某一个元素
target 插入数组中位置
target 在数组所有元素之后
写法一:暴力解法
这道题最为直接的暴力解法,遍历数组中每个元素,只要发现遍历到某个元素 >= target 时直接返回下标,如果遍历完 target 是最大的那就返回 nums.length 直接插入到最后
class Solution {public int searchInsert(int[] nums, int target) {for(int i = 0; i < nums.length; i++) {if(target <= nums[i]) {return i;}}return nums.length;}
}时间复杂度 O(n)
空间复杂度 O(1)
写法二:二分法
使用二分法前提,数组有序,并且无重复元素
确定边界 [left , right]
class Solution {public int searchInsert(int[] nums, int target) {int left = 0, right = nums.length - 1;while(left <= right) {int mid = left + (right - left)/2;if(nums[mid] == target) {return mid;} else if(nums[mid] < target) {left = mid + 1;} else {right = mid - 1;}}// 分析四种上面四种插入的情况// target 在数组所有元素之前 0// target == 数组某个元素 mid// target 插入到数组中某个位置 right + 1 // target 在数组所有元素之后 right + 1return right + 1;}
}时间复杂度 O(log n)
空间复杂度 O(1)
3. 在排序数组中查找元素的第一个和最后一个位置
题目链接:34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109
思路:
寻找 target 在数组中的左右边界,有这三种情况:
target 在数组范围的右边或左边,比如数组 {3,4,5},target = 2 或 target = 6,此时应该返回 {-1,-1}
target 在数组范围中,且数组中不存在 target,比如数组 {3,4,7},target = 6,此时应该返回 {-1,-1}
target 在数组范围中,且数组中存在 target,比如数组 {3,4,5},target = 4,此时应该返回 {1, 1}
下面就是找左右边界了,采用二分法寻找左右边界
写法一:二分法
二分查找,寻找 target 的右边界(不包括 target)
如果 rightBorder 为没有被赋值(即 target 在数组范围的左边,比如 数组 {3,3},target = 2,为了处理这种情况)
class Solution {public int[] searchRange(int[] nums, int target) {int leftBorder = getLeftBorder(nums, target);int rightBorder = getRightBorder(nums, target);// 情况一if (leftBorder == -2 || rightBorder == -2) {return new int[]{-1, -1};} // 情况三if (rightBorder - leftBorder > 1) {return new int[]{leftBorder+1, rightBorder-1};}// 情况二return new int[]{-1, -1};}private int getLeftBorder(int[] nums, int target) {int left = 0, right = nums.length - 1;int leftBorder = -2;while (left <= right) {int mid = left + (right - left)/2;if (target <= nums[mid]) {// 找左边界,nums[mid]==target 时更新 rightright = mid - 1;leftBorder = right;} else {left = mid + 1;}}return leftBorder;}private int getRightBorder(int[] nums, int target) {int left = 0, right = nums.length - 1;int rightBorder = -2;while (left <= right) {int mid = left + (right - left)/2;if (target >= nums[mid]) {//找右边界,nums[mid]==target 时更新 leftleft = mid + 1;rightBorder = left;} else {right = mid - 1;}}return rightBorder;}
}写法二:二分法+双指针(推荐)
在 nums 数组中二分查找 target
如果二分查找失败,则 binarySearch 返回 -1,表名 nums 中没有 target,此时直接返回 {-1,-1}
如果二分查找成功,则 binarySearch 返回 nums 中值为 target 的一个下标,通过左右滑动指针,来找到符合题意的区间
class Solution {public int[] searchRange(int[] nums, int target) {int index = binarySearch(nums, target);if(index == -1) {return new int[]{-1,-1};} int left = index, right = index;while(left - 1 >= 0 && nums[left - 1] == target) {left--;}while(right + 1 <= nums.length - 1 && nums[right + 1] == target) {right++;}return new int[]{left,right};}private int binarySearch(int[] nums, int target) {int left = 0, right = nums.length - 1;while(left <= right) {int mid = left + (right - left)/2;if(target == nums[mid]) {return mid;} else if(target < nums[mid]) {right = mid - 1;} else {left = mid + 1;}}return -1;}
}4. x 的平方根
题目链接:69. x 的平方根 - 力扣(LeetCode)
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 231 - 1
class Solution {public int mySqrt(int x) {long left = 0,right = x,ans = -1;while(left <= right) {long mid = left + (right - left)/2;if((long)(mid*mid) <= x) {ans = mid;left = mid + 1;} else {right = mid - 1;}}return (int)ans;}
}5. 有效的完全平方数
题目链接:367. 有效的完全平方数 - 力扣(LeetCode)
给你一个正整数 num 。如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
完全平方数 是一个可以写成某个整数的平方的整数。换句话说,它可以写成某个整数和自身的乘积。
不能使用任何内置的库函数,如 sqrt 。
示例 1:
输入:num = 16
输出:true
解释:返回 true ,因为 4 * 4 = 16 且 4 是一个整数。
示例 2:
输入:num = 14
输出:false
解释:返回 false ,因为 3.742 * 3.742 = 14 但 3.742 不是一个整数。
提示:
1 <= num <= 231 - 1
class Solution {public boolean isPerfectSquare(int num) {int left = 0, right = num;while(left <= right) {int mid = left + (right - left)/2;long square = (long)mid*mid;if(square > num) {right = mid - 1;} else if(square < num) {left = mid + 1;} else {return true;}}return false;}
}相关文章:

【刷题笔记】之二分查找(搜索插入位置。在排序数组中查找元素的第一个和最后一个位置、x的平方根、有效的完全平方数)
1. 二分查找题目链接 704. 二分查找 - 力扣(LeetCode)给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -…...
)
一起Talk Android吧(第五百一十五回:绘制向外扩散的水波纹)
文章目录整体思路实现方法示例代码各位看官们大家好,上一回中咱们说的例子是"Java中的进制转换",这一回中咱们说的例子是"绘制向外扩散的水波纹"。闲话休提,言归正转, 让我们一起Talk Android吧! 整体思路 …...

基于粒子群改进的支持向量机SVM的情感分类识别,pso-svm情感分类识别
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 SVM应用实例,基于SVM的情感分类预测 代码 结果分析 展望 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型…...
【python中的列表和元组】
文章目录前言一、列表及其使用1.列表的特点2. 列表的使用方法二、元组及其特点1.元组的类型是tuple1.元组的查找操作2. 计算元组某个元素出现的次数3.统计元组内元素的个数总结前言 本文着重介绍python中的列表和元组以及列表和元组之间的区别 一、列表及其使用 1.列表的特点…...

世界顶级五大女程序媛,不仅技术强还都是美女
文章目录1.计算机程序创始人:勒芙蕾丝伯爵夫人2.首位获得图灵奖的女性:法兰艾伦3.谷歌经典首页守护神:玛丽莎梅耶尔4.COBOL之母:葛丽丝穆雷霍普5.史上最强游戏程序媛-余国荔说起程序员的话,人们想到的都会是哪些理工科…...
Linux- 系统随你玩之--文件管理-双生姐妹花
文章目录1、前言2、文件管理-双生姐妹花2.1、 df2.1.1、 df 语法2.1.1 、常用参数2.2、 du2.2.1、du 语法2.1.1、 常用参数2.3、双生姐妹花区别2.3.1、 查看文件统计 的计算方式不同2.3.2 、删除文件情况下统计结果 不同2.3.3 、针对双生姐妹花区别 结语3、双生姐妹花实操3.1 、…...
18、多维图形绘制
目录 一、三维图形绘制 (一)曲线图绘制plot3() (二)网格图绘制 mesh() (三)曲面图绘制 surf() (四)光照模型 surfl() (五)等值线图(等高线图)绘制 cont…...
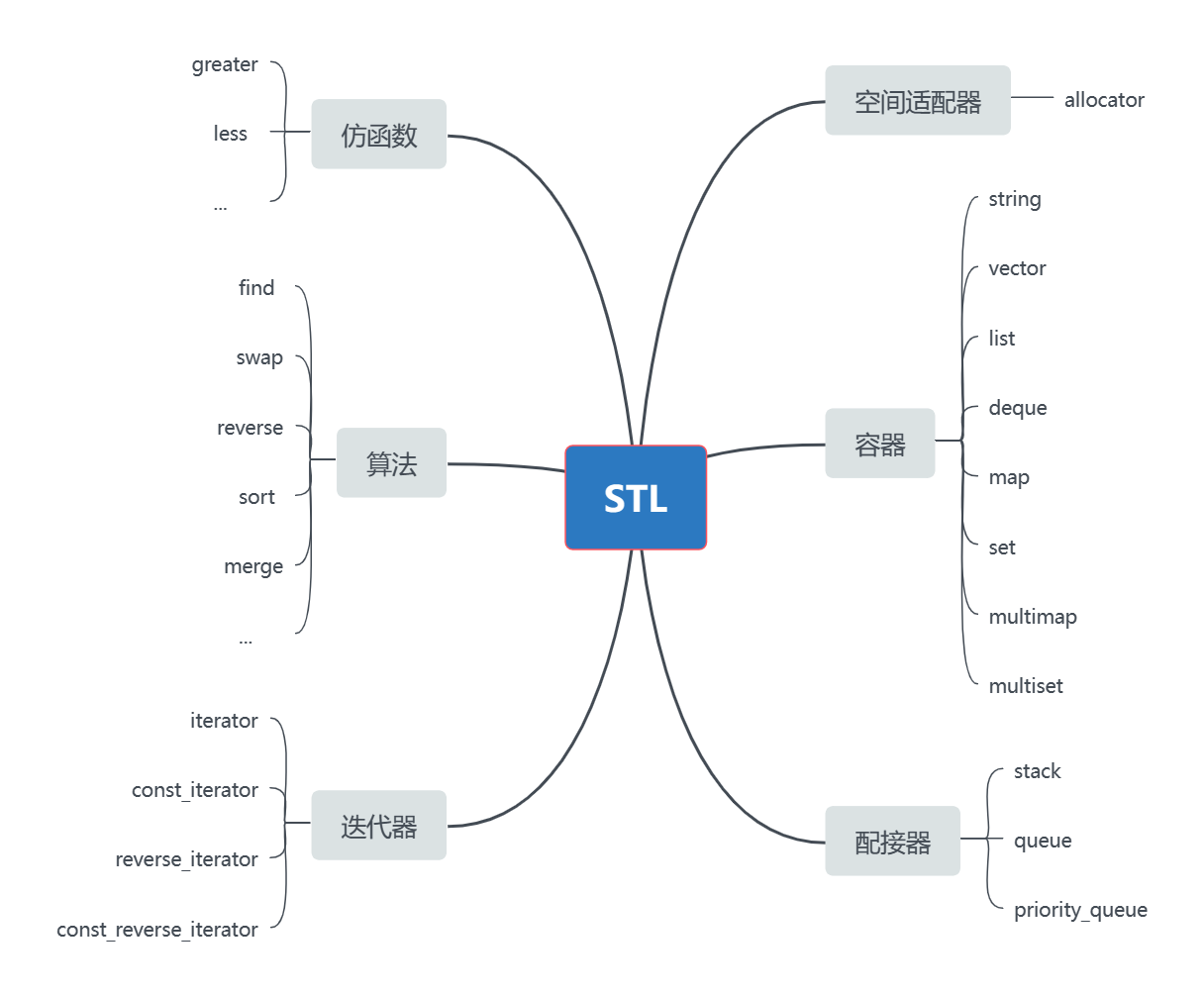
【C++】30h速成C++从入门到精通(STL介绍、string类)
STL简介什么是STLSTL(standard template libaray-标准模板库):是C标准库的重要组成部分,不仅是一个可复用的组件库,而且是一个包罗数据结构与算法的软件框架。STL的版本原始版本Alexander Stepanov、Meng Lee 在惠普实验室完成的原始版本&…...

PMP是什么意思?适合哪些人学呢?
PMP简而言之,就是提高项目管理理论基础和实践能力的考试。 官方一点的说明呢,就是:PMP证书全称为Project Management Professional,也叫项目管理专业人士资格认证。 PMP证书由美国项目管理协会(PMI)发起,是严格评估项…...

【SpringBoot 事务不回滚?怎么解决?】
SpringBoot 事务不回滚可能有多种原因,下面列举一些常见的原因和对应的解决方法: 异常被捕获处理了 如果方法中抛出了异常,但是在方法中被捕获并处理了,那么事务不会回滚。解决方法是让异常继续抛出,或者使用 Transa…...

软件研发管理经验总结 - 技术管理
软件研发管理经验总结 - 技术管理 技术管理主要负责有技术团队建设、管理团队成员技术相关事务、帮助团队成员成长、负责团队成员交付的代码质量、以及负责产品技术方向、以及产品相关前沿技术调研;管理团队成员技术相关事务有代码Review、故障率跟踪、分析及根据分…...

项目实战典型案例19——临时解决方案和最终解决方案
临时解决方案和最终解决方案一:背景介绍二:思路&方案四:总结五:升华一:背景介绍 本篇博客是对项目开发中出现的临时解决方案和最终解决方案进行的总结和改进。目的是将经历转变为自己的经验。通过博客的方式分享给…...

机器学习模型的可解释性算法汇总!
模型可解释性汇总简 介目前很多机器学习模型可以做出非常好的预测,但是它们并不能很好地解释他们是如何进行预测的,很多数据科学家都很难知晓为什么该算法会得到这样的预测结果。这是非常致命的,因为如果我们无法知道某个算法是如何进行预测&…...

什么是着色器/Threejs如何使用着色器/Threejs使用着色器实现平面网格的动态效果案例
1,什么是着色器着色器(Shader)是计算机图形学中的一个重要概念,它是在 GPU 上运行的程序,用于计算三维场景中每个像素的颜色和其他属性。着色器通常分为两种类型:顶点着色器和片元着色器。顶点着色器主要用…...
191、【动态规划】AcWing ——AcWing 900. 整数划分:完全背包解法+加减1解法(C++版本)
题目描述 参考文章:900. 整数划分 解题思路 因为本题中规定了数字从大到小,其实也就是不论是1 2 1 4,还是2 1 1 4,都会被看作是2 1 1 4这一种情况,因此本题是在遍历中不考虑结果顺序。 背包问题中只需考虑…...

Java 比较器
public interface Comparable Comparable 接口位于 java.lang 包下,对实现它的每个类的对象强加一个总排序,这种排序被称为类的自然顺序,compareTo 方法被称为其自然比较方法。 实现此接口的对象的列表(和数组)可以由…...

配置本地 python GEE、geemap环境
1.安装anconda 百度搜索anconda清华镜像,从清华镜像中选择最新的anconda安装包,国内镜像网站下载速度较快,如果从国外官网下载速度相当慢,详细安装教程请参考: anconda安装教程https://blog.csdn.net/lwbCUMT/article…...
cmd命令教程
小提示: 在本文中,我将向您展示可以在 Windows 命令行上使用的 40 个命令 温馨提示:在本教程中学习使用适用于 Windows 10 和 CMD 网络命令的最常见基本 CMD 命令及其语法和示例 文章目录为什么命令提示符有用一、cmd是什么?如何在…...

深圳大学计软《面向对象的程序设计》实验15 函数模板和类模板
A. 有界数组模板类(类模板) 题目描述 编写有界数组模板BoundArray(即检查对数组元素下标引用并在下标越界时终止程序的执行),能够存储各种类型的数据。要求实现对数组进行排序的方法sort,及对数组进行查找…...
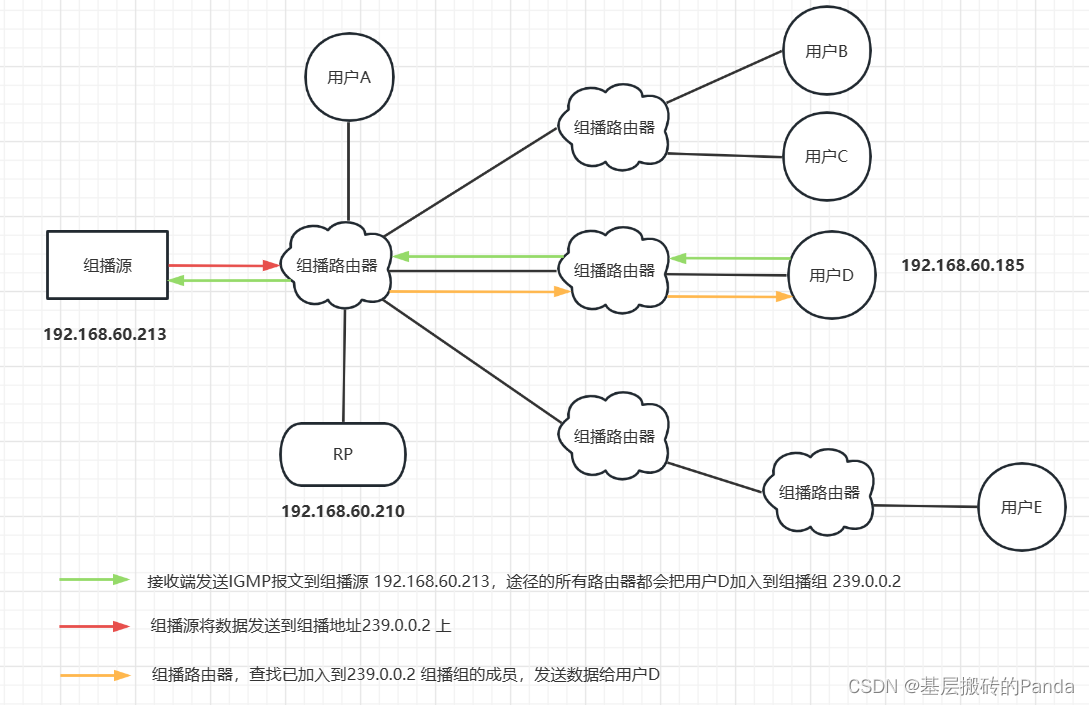
组播详解及示例代码
写在前面 由于公司业务需要用到组播实现,这里就记录下学习过程。在学习组播之前,我们先来看看另外两种数据包传输方式:单播和广播。 单播:简单来说就是数据一对一发送,如果需要给多个主机发送数据时,就需…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
