2024年美赛 (D题ICM)| 湖流网络水位控制 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。
让我们来看看美赛的D题!
完整内容可以在文章末尾领取!

问题重述
问题 D 背景:
美国和加拿大的五大湖是世界上最大的淡水湖群。这些湖泊和相连的水道构成了一个庞大的排水区,涵盖了这两个国家的许多大城市,具有多样的气候和局部天气条件。
湖泊的水被用于许多目的(捕鱼、娱乐、发电、饮用水、航运、动植物栖息地、建筑、灌溉等)。因此,许多利益相关者对湖泊的水流管理有兴趣。主要问题是调节水位,以使所有利益相关者受益。
湖泊中的水位取决于进出湖泊的水量。这些水位是温度、风、潮汐、降水、蒸发、湖底形状、河流流量和径流、水库政策、季节性循环以及长期气候变化之间复杂相互作用的结果。在整个大湖系统中有两个主要的控制机制——苏圣玛丽的补偿工程(三个水电厂、五个航道船闸和急流头部的闸门坝)和康沃尔的摩西-桑德斯大坝,如在附件中所示。
虽然两个控制大坝、许多水道和运河以及排水区水库可能受人类控制,但雨水、蒸发、侵蚀、冰封等水流现象的速率是超出人类操纵的。地方法规的政策可能产生意想不到的效果,季节性和水盆环境的变化也可能影响水盆的生态系统,从而影响湖泊和周围地区的植物和动物的健康。尽管大湖地区似乎有规律的年度模式,但水位的两到三英尺的偏差可能会极大地影响一些利益相关者。
这是一个“邪恶”的动态网络流问题——由于相互依赖关系、复杂的要求和固有的不确定性,解决起来非常具有挑战性。对于湖泊问题,我们面临着不断变化的动态和利益相关者的冲突。
问题 D 要求:
国际联合委员会(IJC)请求贵公司国际网络控制建模者(ICM)协助管理和模拟直接影响五大湖流网络水位的控制机制(如补偿工程和摩西-桑德斯大坝,在附件中有说明)。您的ICM主管已经委托您的团队在开发模型和实施模型的管理计划方面发挥领导作用。您的主管表示,有几个考虑因素可能有助于实现这个目标,首先是建立五大湖及其连接河流的网络模型,从苏必尔湖到大西洋。您的主管提到的一些建议性的考虑或问题还包括:
- 建立五大湖及其连接河流的网络模型,以确定最佳水位,并考虑各利益相关者的需求。
- 制定算法,根据湖泊的流入和流出数据来维持最佳水位。
- 分析控制算法对大坝流出的敏感性,并评估新的控制方法是否会带来更好的结果。
- 评估算法对环境条件变化的敏感性,如降水、冬季积雪、冰封等。
- 集中关注安大略湖的利益相关者和因素,提出针对该湖水位管理的解决方案。
- 基于历史数据制定模型和管理策略,并与先前模型进行比较。
最终的解决方案需要包括网络模型、算法设计、对历史数据的分析、针对安大略湖的管理方案以及对AI工具的使用报告。
问题一
为解决问题一,建立五大湖及其连接河流的网络模型,我们需要考虑水位的变化、流量的调整,以及各利益相关者的需求。以下是一个简化的建模思路,其中包含一些可能的函数表达式:
1. 水位建模:
每个湖泊的水位变化可以使用简化的微分方程表示,考虑流入、流出和自然波动:
d h i d t = Inflow i − Outflow i + NaturalFluctuations i \frac{dh_i}{dt} = \text{Inflow}_i - \text{Outflow}_i + \text{NaturalFluctuations}_i dtdhi=Inflowi−Outflowi+NaturalFluctuationsi
其中:
- h i h_i hi 表示湖泊 i i i 的水位。
- Inflow i \text{Inflow}_i Inflowi 表示流入湖泊 i i i 的总流量。
- Outflow i \text{Outflow}_i Outflowi 表示流出湖泊 i i i 的总流量。
- NaturalFluctuations i \text{NaturalFluctuations}_i NaturalFluctuationsi 表示自然波动的影响。
2. 利益相关者需求建模:
每个湖泊的利益相关者需求可以使用需求函数表示,考虑到水位对各利益相关者的影响。例如,对于湖泊 i i i 的需求函数可能如下:
Demand i = a i ⋅ ( h i − b i ) 2 + c i \text{Demand}_i = a_i \cdot (h_i - b_i)^2 + c_i Demandi=ai⋅(hi−bi)2+ci
其中:
- Demand i \text{Demand}_i Demandi 表示湖泊 i i i 的总需求。
- a i a_i ai、 b i b_i bi、 c i c_i ci 是与湖泊 i i i 特定的参数,用于调整需求函数的形状。
3. 流量调整算法:
为了维持最佳水位,需要设计一个流量调整算法。一个简单的算法可以基于水位与最佳水位的差异进行调整:
Adjustment i = k ⋅ ( h target i − h i ) \text{Adjustment}_i = k \cdot (h_{\text{target}_i} - h_i) Adjustmenti=k⋅(htargeti−hi)
其中:
- h target i h_{\text{target}_i} htargeti 表示湖泊 i i i 的目标水位。
- k k k 是调整系数,用于控制调整的速度。
4. 目标函数:
考虑到最小化总成本或最大化总效益,可以设计一个目标函数:
Objective = ∑ i ( Cost i ⋅ Inflow i + Benefit i ⋅ Demand i ) \text{Objective} = \sum_{i} \left( \text{Cost}_i \cdot \text{Inflow}_i + \text{Benefit}_i \cdot \text{Demand}_i \right) Objective=∑i(Costi⋅Inflowi+Benefiti⋅Demandi)
其中:
- Cost i \text{Cost}_i Costi 表示湖泊 i i i 流入的成本系数。
- Benefit i \text{Benefit}_i Benefiti 表示湖泊 i i i 的需求满足带来的效益系数。
5. 参数设定和模拟:
设定初始条件,包括各湖泊的初始水位、流量等。使用数值模拟方法(如欧拉法或四阶龙格-库塔法)模拟系统的演化。
6. 模型评估:
通过与历史数据对比,验证模型的准确性。评估利益相关者的满意度和模型对环境条件变化的敏感性。
import numpy as np
import matplotlib.pyplot as pltclass LakeModel:def __init__(self, num_lakes, simulation_time, delta_t, inflows, outflows):self.num_lakes = num_lakesself.simulation_time = simulation_timeself.delta_t = delta_tself.inflows = inflowsself.outflows = outflowsself.water_levels = np.zeros((num_lakes, simulation_time))def initialize_water_levels(self, initial_levels):self.water_levels[:, 0] = initial_levelsdef demand_function(self, water_level, demand_params):# 一个简单的需求函数示例a, b, c = demand_paramsreturn a * (water_level - b)**2 + cdef adjust_flow(self, target_level, current_level, adjustment_coeff):# 一个简单的流量调整算法示例return adjustment_coeff * (target_level - current_level)def simulate(self):for t in range(1, self.simulation_time):for i in range(self.num_lakes):# 水位变化模型demand = self.demand_function(self.water_levels[i, t-1], [1, 5, 0])adjustment = self.adjust_flow(demand, self.water_levels[i, t-1], 0.1)# 更新水位self.water_levels[i, t] = self.water_levels[i, t-1] + (self.inflows[i, t] - self.outflows[i, t] + adjustment) * self.delta_tdef visualize(self):for i in range(self.num_lakes):plt.plot(range(self.simulation_time), self.water_levels[i, :], label=f'Lake {i+1}')plt.xlabel('Time')plt.ylabel('Water Level')plt.legend()plt.show()# 模拟参数
num_lakes = 5
simulation_time = 100
delta_t = 1
inflows = np.random.rand(num_lakes, simulation_time)
outflows = np.random.rand(num_lakes, simulation_time)# 创建模型实例
lake_model = LakeModel(num_lakes, simulation_time, delta_t, inflows, outflows)# 初始条件见完整代码
问题二
建模思路:
问题二 - 最优水位控制及灵敏性分析
1. 最佳水位建模:
1.1. 利益相关者需求函数:
为每个湖泊 i i i 引入二次函数作为需求函数:
Demand i = a i ⋅ ( h i − b i ) 2 + c i \text{Demand}_i = a_i \cdot (h_i - b_i)^2 + c_i Demandi=ai⋅(hi−bi)2+ci
其中 h i h_i hi 表示湖泊 i i i 的水位, a i a_i ai、 b i b_i bi、 c i c_i ci 是需求函数参数。
1.2. 目标函数:
定义总体目标函数,以最大化总体效益或最小化总成本:
Objective = ∑ i ( Benefit i ⋅ Demand i − Cost i ⋅ Inflow i ) \text{Objective} = \sum_{i} \left( \text{Benefit}_i \cdot \text{Demand}_i - \text{Cost}_i \cdot \text{Inflow}_i \right) Objective=∑i(Benefiti⋅Demandi−Costi⋅Inflowi)
2. 优化算法选择 - 遗传算法:
利用遗传算法进行水位优化:
- 初始化种群: 随机生成一组初始解作为种群。
- 适应度评估: 计算每个个体的适应度,即目标函数值。
- 选择: 根据适应度选择个体,更适应的个体被选择的概率更高。
- 交叉: 对选定的个体进行基因交叉,生成新的个体。
- 变异: 对新生成的个体进行变异,引入一些随机性。
- 替换: 根据一定规则替换原有种群中的个体。
- 重复: 重复进行选择、交叉、变异、替换的过程,直至达到停止条件。
3. 调整算法设计:
设计一个调整算法,根据当前水位和目标水位,调整湖泊的流量以接近目标水位:
Adjustment i = k ⋅ ( h target i − h i ) \text{Adjustment}_i = k \cdot (h_{\text{target}_i} - h_i) Adjustmenti=k⋅(htargeti−hi)
4. 模型实施:
- 模拟优化过程: 在每个迭代中,通过调整水位,使用遗传算法找到最佳水位配置。
- 整合调整算法: 在每个时间步骤中,根据优化算法确定的水位,使用调整算法调整湖泊的流量。
5. 结果评估:
- 模拟结果验证: 使用模型进行模拟,验证最终水位配置是否满足各利益相关者的需求,与历史数据进行比较。
- 效益和成本评估: 评估优化算法找到的最佳水位配置对各湖泊的效益和成本的影响。
6. 灵敏性分析:
- 单因素灵敏性分析: 逐一变化模型中的每个参数,观察模型输出的变化。
- 敏感性指标计算: 计算参数变化对最终目标函数值的影响程度。
- 参数范围分析: 确定每个参数的合理范围,观察在这个范围内模型的输出如何变化。
- 随机性分析: 考虑模型中的随机性因素,通过多次运行模型并观察结果的统计分布,评估模型的鲁棒性。
7. 优化和迭代:
- 模型优化: 根据评估结果对模型进行优化,可能需要调整模型中的参数、算法或需求函数。
- 利益相关者反馈: 与利益相关者合作,获取他们的反馈,并根据需要调整模型。可能需要一个迭代的过程,直到获得满意的模型。
import numpy as np
from scipy.optimize import minimize# 模拟湖泊数量
num_lakes = 5# 需求函数参数 (a, b, c)
demand_params = np.random.rand(num_lakes, 3)# 效益和成本系数
benefit_coefficients = np.random.rand(num_lakes)
cost_coefficients = np.random.rand(num_lakes)# 初始水位配置
initial_water_levels = np.zeros(num_lakes)# 遗传算法参数
population_size = 20
generations = 50# 目标函数
def objective_function(h):total_objective = 0for i in range(num_lakes):demand_i = demand_params[i, 0] * (h[i] - demand_params[i, 1])**2 + demand_params[i, 2]total_objective += benefit_coefficients[i] * demand_i - cost_coefficients[i] * h[i]return -total_objective # 因为我们是在最小化目标函数# 遗传算法
def genetic_algorithm(objective_func, initial_population, bounds, generations):population = initial_populationfor gen in range(generations):# 适应度评估fitness = [objective_func(ind) for ind in population]# 选择selected_indices = np.argsort(fitness)[:population_size]selected_population = [population[i] for i in selected_indices]# 交叉和变异new_population = crossover_and_mutate(selected_population, bounds)population = new_population# 返回最终结果return min(population, key=objective_func)# 交叉和变异操作
def crossover_and_mutate(selected_population, bounds):new_population = []for parent1 in selected_population:parent2 = selected_population[np.random.choice(len(selected_population))]crossover_point = np.random.randint(num_lakes)child = np.concatenate((parent1[:crossover_point], parent2[crossover_point:]))child += np.random.normal(0, 1, size=num_lakes) # 添加一些变异# 限制水位在合理范围内child = np.clip(child, bounds[:, 0], bounds[:, 1])new_population.append(child)return new_population# 设置水位范围
bounds = np.array([(0, 100)] * num_lakes)# 遗传算法优化
initial_population = np.random.uniform(bounds[:, 0], bounds[:, 1], size=(population_size, num_lakes))
optimal_water_levels_genetic = genetic_algorithm(objective_function, initial_population, bounds, generations)# 输出遗传算法优化结果
print("Optimal Water Levels (Genetic Algorithm):", optimal_water_levels_genetic)
print("Optimal Objective Value (Genetic Algorithm):", -objective_function(optimal_water_levels_genetic))# 简单灵敏性分析
sensitivity_results = []
for i in range(num_lakes):perturbed_water_levels = optimal_water_levels_genetic.copy()perturbed_water_levels[i] += 1.0 # 在第i个湖泊的水位上添加微小扰动perturbed_objective = -objective_function(perturbed_water_levels)sensitivity = perturbed_objective + objective_function(optimal_water_levels_genetic)#见完整版
问题三
建模思路:
1. 建立状态空间模型:
湖泊水位的状态空间模型表示为:
x k + 1 = A x k + B u k + w k x_{k+1} = Ax_k + Bu_k + w_k xk+1=Axk+Buk+wk
其中:
- $ x_k$ 是系统状态向量,包括湖泊水位及其它相关状态。
- $ u_k$ 是控制输入向量,表示水流的调整。
- $ A$ 和 $ B$ 是状态转移矩阵。
- $ w_k$ 是过程噪声。
2. 设定控制目标:
设定湖泊水位的目标向量为 $ x_{\text{target}}$。
3. 设计控制目标函数:
目标函数最小化系统状态与目标状态之间的差异:
J = ∑ k = 0 N ∥ x k − x target ∥ 2 J = \sum_{k=0}^{N} \|x_k - x_{\text{target}}\|^2 J=∑k=0N∥xk−xtarget∥2
4. 确定系统约束:
系统约束表示为:
C x k ≤ D Cx_k \leq D Cxk≤D
其中 $ C$ 和 $ D$ 是相应的约束矩阵。
5. 预测未来系统状态:
使用模型,预测未来 $ N$ 个时间步骤内的系统状态:
x ^ k + j ∣ k = A j x k + ∑ i = 0 j − 1 A i B u k + j − i − 1 \hat{x}_{k+j|k} = A^j x_k + \sum_{i=0}^{j-1} A^{i}Bu_{k+j-i-1} x^k+j∣k=Ajxk+∑i=0j−1AiBuk+j−i−1
6. 优化控制输入:
通过求解以下优化问题选择最优控制输入:
min u k J = ∑ j = 0 N − 1 ∥ x ^ k + j ∣ k − x target ∥ 2 \min_{u_k} J = \sum_{j=0}^{N-1} \| \hat{x}_{k+j|k} - x_{\text{target}} \|^2 minukJ=∑j=0N−1∥x^k+j∣k−xtarget∥2
subject to C x k ≤ D \text{subject to } Cx_k \leq D subject to Cxk≤D
7. 实施控制:
将优化得到的控制输入 $ u_k^*$ 应用于湖泊系统:
u k = u k ∗ u_k = u_k^* uk=uk∗
8. 重复过程:
重复上述步骤,每个时间步骤都重新优化控制输入,考虑新的系统状态。
9. 灵敏性分析:
9.1 参数灵敏性:
Sensitivity k = ∂ J ∂ k \text{Sensitivity}_{k} = \frac{\partial J}{\partial k} Sensitivityk=∂k∂J
9.2 初始水位灵敏性:
Sensitivity Initial = ∂ J ∂ x 0 \text{Sensitivity}_{\text{Initial}} = \frac{\partial J}{\partial x_0} SensitivityInitial=∂x0∂J
10. 优化和迭代:
基于灵敏性分析结果,优化 MPC 控制算法的参数,可能需要多次迭代以达到最优性能。
模型预测控制(MPC)算法简介:
1. 概述:
模型预测控制(Model Predictive Control, MPC)是一种先进的控制策略,它使用系统的动态模型进行预测,以优化未来一系列时间步骤内的控制输入,从而实现对系统的有效控制。
2. 基本思想:
MPC 的基本思想是在每个时间步骤上优化控制输入,然后实施系统的第一个控制输入。在下一个时间步骤,重新优化,考虑新的系统状态,并重复这个过程。这种迭代的方法使得MPC适用于多变量、多约束的系统。
3. 主要步骤:
-
系统建模: 建立描述系统动态行为的数学模型,通常为状态空间模型。
-
设定控制目标: 定义系统的目标,例如期望的状态或输出。
-
设计目标函数: 构建优化问题的目标函数,通常为最小化系统状态与目标之间的差异。
-
确定约束条件: 考虑系统约束,例如输入限制、状态约束等。
-
预测未来系统状态: 使用建模过程,预测未来一段时间内的系统状态。
-
优化控制输入: 在每个时间步骤上,通过求解优化问题来选择最优的控制输入,以最小化目标函数并满足约束条件。
-
实施控制: 应用优化得到的控制输入到实际系统。
-
迭代过程: 重复上述步骤,每个时间步骤都重新优化控制输入,考虑新的系统状态。
4. 优点:
- MPC 能够处理多变量系统,并考虑多个控制目标和约束。
- 通过使用系统模型进行预测,可以在考虑约束的同时优化控制输入。
- 适用于非线性、时变和受约束的系统。
5. 在水位控制中的应用:
在水位控制问题中,MPC可以通过优化水流的调整来维持湖泊水位在期望范围内。通过建模湖泊的水量平衡等动态特性,MPC可以在考虑约束的情况下,实现水位的精确调控,以满足各利益相关者的需求。
import numpy as np
from scipy.optimize import minimize# 湖泊水位控制的简化模型参数
A = np.array([[0.8]])
B = np.array([[0.2]])
C = np.array([[1]])
D = np.array([[0]])# 控制参数
k = 0.1# 初始水位
initial_water_level = 5.0# 目标水位
target_water_level = 7.0# 控制算法
def control_algorithm(current_water_level):adjustment = k * (target_water_level - current_water_level)return adjustment# 优化目标函数
def objective_function(control_inputs):# 模拟湖泊水位的变化water_levels = [initial_water_level]for control_input in control_inputs:water_level = A.dot(water_levels[-1]) + B.dot(control_input)water_levels.append(water_level)# 计算目标函数,最小化水位与目标水位的差异objective = sum((C.dot(np.array(water_levels)) - target_water_level)**2)return objective# 约束条件
def constraint_function(control_inputs):# 可以加入额外的约束条件,例如输入的范围等return np.array([])# 优化问题求解
initial_guess = np.zeros(10) # 初始猜测的控制输入
result = minimize(objective_function, initial_guess, constraints={'type': 'eq', 'fun': constraint_function})# 输出优化结果
optimized_control_inputs = result.x
print("Optimized Control Inputs:", optimized_control_inputs)# 应用优化得到的控制输入见完整版
问题四
1. 敏感性分析模型建立:
1.1 敏感性指标:
我们选择水位控制性能的均方根误差(RMSE)作为敏感性指标,这是一种常用于衡量模型预测精度的指标。其计算公式为:
RMSE = 1 N ∑ i = 1 N ( x i − x ^ i ) 2 \text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \hat{x}_i)^2} RMSE=N1∑i=1N(xi−x^i)2
1.2 环境条件变量:
我们考虑三个可能影响水位控制的环境条件变量:
- 降雨量(Rainfall)
- 融雪量(Snowmelt)
- 外部温度(Temperature)
1.3 关系模型:
我们建立系统性能(RMSE)与环境条件变量之间的关系。假设模型为线性关系:
RMSE = a ⋅ Rainfall + b ⋅ Snowmelt + c ⋅ Temperature + ϵ \text{RMSE} = a \cdot \text{Rainfall} + b \cdot \text{Snowmelt} + c \cdot \text{Temperature} + \epsilon RMSE=a⋅Rainfall+b⋅Snowmelt+c⋅Temperature+ϵ
其中, a , b , c a, b, c a,b,c 是待估计的系数, ϵ \epsilon ϵ 是随机误差。
2. 敏感性分析算法:
2.1 参数敏感性:
通过有限差分法,我们估计系数 a , b , c a, b, c a,b,c 对 RMSE 的敏感性。假设我们以 δ = 0.01 \delta = 0.01 δ=0.01 为例:
Sensitivity a = RMSE ( a + δ , b , c ) − RMSE ( a − δ , b , c ) 2 δ \text{Sensitivity}_{a} = \frac{\text{RMSE}(a + \delta, b, c) - \text{RMSE}(a - \delta, b, c)}{2 \delta} Sensitivitya=2δRMSE(a+δ,b,c)−RMSE(a−δ,b,c)
类似地,计算 Sensitivity b \text{Sensitivity}_{b} Sensitivityb 和 Sensitivity c \text{Sensitivity}_{c} Sensitivityc。
2.2 初始条件敏感性:
尝试不同的初始水位条件,观察 RMSE 的变化。例如,比较新的初始水位条件和原始初始水位条件下的 RMSE。
Sensitivity Initial = RMSE ( New Initial Condition ) − RMSE ( Original Initial Condition ) Original Initial Condition \text{Sensitivity}_{\text{Initial}} = \frac{\text{RMSE}(\text{New Initial Condition}) - \text{RMSE}(\text{Original Initial Condition})}{\text{Original Initial Condition}} SensitivityInitial=Original Initial ConditionRMSE(New Initial Condition)−RMSE(Original Initial Condition)
2.3 外部环境敏感性:
变化降雨量、融雪量、外部温度,观察 RMSE 的变化。以降雨量为例:
Sensitivity Rainfall = RMSE ( Rainfall + δ , S n o w m e l t , T e m p e r a t u r e ) − RMSE ( Rainfall , S n o w m e l t , T e m p e r a t u r e ) δ \text{Sensitivity}_{\text{Rainfall}} = \frac{\text{RMSE}(\text{Rainfall} + \delta, Snowmelt, Temperature) - \text{RMSE}(\text{Rainfall}, Snowmelt, Temperature)}{\delta} SensitivityRainfall=δRMSE(Rainfall+δ,Snowmelt,Temperature)−RMSE(Rainfall,Snowmelt,Temperature)
类似地,计算 Sensitivity Snowmelt \text{Sensitivity}_{\text{Snowmelt}} SensitivitySnowmelt 和 Sensitivity Temperature \text{Sensitivity}_{\text{Temperature}} SensitivityTemperature。
3. 综合分析:
综合以上敏感性分析的结果,可以得出关于控制算法对于不同环境条件的鲁棒性评估。例如,可以比较不同敏感性指标的相对重要性,以全面评估算法在不同情境下的性能表现。
4. 示例公式:
以参数敏感性为例,有:
Sensitivity a = RMSE ( a + δ , b , c ) − RMSE ( a − δ , b , c ) 2 δ \text{Sensitivity}_{a} = \frac{\text{RMSE}(a + \delta, b, c) - \text{RMSE}(a - \delta, b, c)}{2 \delta} Sensitivitya=2δRMSE(a+δ,b,c)−RMSE(a−δ,b,c)
同样的方法可以应用于 b b b 和 c c c 的敏感性计算。
import numpy as np
from scipy.optimize import minimize# 模型参数
a, b, c = 1.0, 0.5, 0.2 # 示例参数,实际应用中需要根据模型进行调整
delta = 0.01# 模拟水位数据
N = 100
rainfall = np.random.rand(N)
snowmelt = np.random.rand(N)
temperature = np.random.rand(N)# 模拟实际水位数据(示例,实际应用中应替换为真实数据)
actual_water_level = a * rainfall + b * snowmelt + c * temperature + np.random.normal(0, 0.1, N)# 模型预测水位
def predict_water_level(a, b, c, rainfall, snowmelt, temperature):return a * rainfall + b * snowmelt + c * temperature# 计算RMSE
def calculate_rmse(actual, predicted):return np.sqrt(np.mean((actual - predicted)**2))# 优化目标函数(用于有限差分法的最小化)
def objective_function(params, a, b, c, delta, rainfall, snowmelt, temperature, actual):new_a, new_b, new_c = paramspredicted_water_level = predict_water_level(new_a, new_b, new_c, rainfall, snowmelt, temperature)return calculate_rmse(actual, predicted_water_level)# 有限差分法估计参数敏感性
def calculate_parameter_sensitivity(param_index, a, b, c, delta, rainfall, snowmelt, temperature, actual):params = [a, b, c]params[param_index] += deltarmse_plus_delta = objective_function(params, a, b, c, delta, rainfall, snowmelt, temperature, actual)params[param_index] -= 2 * deltarmse_minus_delta = objective_function(params, a, b, c, delta, rainfall, snowmelt, temperature, actual)params[param_index] += delta # 恢复原始参数值sensitivity = (rmse_plus_delta - rmse_minus_delta) / (2 * delta)return sensitivity#见完整
问题五
问题五建模思路:
1. Lake Ontario 水位管理模型:
1.1 水位控制因素:
- 湖泊补给源: 入湖流量 I ( t ) I(t) I(t)
- 湖泊排水源: 排水流量 O ( t ) O(t) O(t)
- 湖泊蒸发: 蒸发量 E ( t ) E(t) E(t)
- 湖泊降雨: 降雨量 R ( t ) R(t) R(t)
- 湖泊人工控制: 人工控制量 U ( t ) U(t) U(t)
1.2 水位模型:
湖泊水位模型可以采用动态水库模型:
d h d t = I ( t ) − O ( t ) − E ( t ) + R ( t ) + U ( t ) \frac{dh}{dt} = I(t) - O(t) - E(t) + R(t) + U(t) dtdh=I(t)−O(t)−E(t)+R(t)+U(t)
2. 利益相关方和目标分析:
2.1 利益相关方:
- 当地居民: 洪水风险降低、水质保护。
- 渔业: 水生态系统保护。
- 航运公司: 航运通畅度。
- 政府机构: 水资源管理和环境保护。
2.2 目标:
- 洪水风险控制: $ \min \int (h - h_{\text{target}})^2 , dt $
- 生态保护: $ \max \int E(t) , dt $
- 航运通畅: $ \max \int U(t) , dt $
3. 模型优化与算法选择:
3.1 优化目标:
多目标优化问题:
minimize J ( h , E , U ) = α ∫ ( h − h target ) 2 d t − β ∫ E ( t ) d t − γ ∫ U ( t ) d t \text{minimize} \, J(h, E, U) = \alpha \int (h - h_{\text{target}})^2 \, dt - \beta \int E(t) \, dt - \gamma \int U(t) \, dt minimizeJ(h,E,U)=α∫(h−htarget)2dt−β∫E(t)dt−γ∫U(t)dt
其中, α , β , γ \alpha, \beta, \gamma α,β,γ 是权重系数。
3.2 算法选择:
采用多目标遗传算法(MOGA)进行优化。
4. 环境条件敏感性分析:
Sensitivity Rainfall = ∂ h ∂ R ( t ) \text{Sensitivity}_{\text{Rainfall}} = \frac{\partial h}{\partial R(t)} SensitivityRainfall=∂R(t)∂h
Sensitivity Temperature = ∂ h ∂ T ( t ) \text{Sensitivity}_{\text{Temperature}} = \frac{\partial h}{\partial T(t)} SensitivityTemperature=∂T(t)∂h
Sensitivity Area = ∂ h ∂ A ( t ) \text{Sensitivity}_{\text{Area}} = \frac{\partial h}{\partial A(t)} SensitivityArea=∂A(t)∂h
5. 历史数据分析:
使用历史数据进行参数估计和模型验证:
J hist ( h , E , U ) = α ∫ ( h − h observed ) 2 d t − β ∫ E ( t ) d t − γ ∫ U ( t ) d t J_{\text{hist}}(h, E, U) = \alpha \int (h - h_{\text{observed}})^2 \, dt - \beta \int E(t) \, dt - \gamma \int U(t) \, dt Jhist(h,E,U)=α∫(h−hobserved)2dt−β∫E(t)dt−γ∫U(t)dt
6. 实时监测与调整:
实时监测系统通过观测数据更新模型参数:
J real-time ( h , E , U ) = α ∫ ( h − h target ) 2 d t − β ∫ E ( t ) d t − γ ∫ U ( t ) d t J_{\text{real-time}}(h, E, U) = \alpha \int (h - h_{\text{target}})^2 \, dt - \beta \int E(t) \, dt - \gamma \int U(t) \, dt Jreal-time(h,E,U)=α∫(h−htarget)2dt−β∫E(t)dt−γ∫U(t)dt
7. 决策支持系统:
提供决策支持系统可视化多目标优化结果和实时水位信息。
import numpy as np
from scipy.integrate import quad
from scipy.optimize import differential_evolution# 示例数据,需要替换为实际数据
h_target = 10.0
h_observed = np.random.rand(100) * 5 + 5 # 模拟观测到的水位
E = np.random.rand(100) # 模拟蒸发量
U = np.random.rand(100) # 模拟人工控制量
R = np.random.rand(100) # 模拟降雨量# 权重系数
alpha, beta, gamma = 1.0, 0.1, 0.1# 目标函数
def objective_function(params):h, E, U = paramsJ1 = alpha * np.sum((h - h_target)**2)J2 = -beta * np.sum(E)J3 = -gamma * np.sum(U)return J1 + J2 + J3# 约束条件函数(水位模型)
def water_level_model(params):h, E, U = paramsdh_dt = quad(lambda t: R[t] - E[t] + U[t], 0, len(R) - 1)[0]return h - h_observed + dh_dt# 优化参数范围
bounds = [(0, 20), (0, 1), (0, 1)]#见完整
问题六
1. 历史数据分析:
1.1 数据预处理:
- 数据清理: 使用插值或平均值填充缺失值,检测并修正异常值。
# 举例:使用线性插值填充缺失值
df['column'].interpolate(method='linear', inplace=True)
- 数据重采样: 将数据按月或季度进行重采样,确保数据具有一致的时间尺度。
# 举例:按月重采样
df_resampled = df.resample('M').mean()
1.2 水位模型校准:
- 参数校准: 使用历史数据进行参数估计,最小化模型模拟结果与观测值的误差。
# 举例:使用最小二乘法进行参数估计
from scipy.optimize import curve_fitdef water_level_model(t, a, b, c):return a * np.sin(b * t) + cparams, covariance = curve_fit(water_level_model, time_points, observed_data)
2. 效果评估与管理策略:
2.1 优化后的模型评估:
- 模型误差计算: 比较校准后模型模拟结果与实际观测值,计算误差指标。
# 举例:计算均方根误差(RMSE)
from sklearn.metrics import mean_squared_errorrmse = np.sqrt(mean_squared_error(observed_data, simulated_data))
2.2 管理策略评估:
- 管理策略效果指标: 比较历史数据中采用的管理策略和模型仿真结果,评估管理策略的效果。
# 举例:比较实际观测值和模拟值
strategy_effectiveness = calculate_effectiveness(observed_data, simulated_data)
3. 灵敏性分析:
3.1 参数灵敏性:
- 参数灵敏性分析: 通过改变水位模型中的关键参数,分析模型对参数变化的灵敏性。
# 举例:计算参数灵敏性
sensitivity_to_parameter = calculate_sensitivity_to_parameter(model, parameters, observed_data)
3.2 控制策略灵敏性:
- 策略灵敏性分析: 评估控制策略对不同环境条件和需求变化的适应性。
# 举例:计算控制策略灵敏性
sensitivity_to_strategy = calculate_sensitivity_to_strategy(model, strategy, observed_data)
4. 决策支持系统的改进:
- 模型改进和实时监测系统更新: 根据历史数据分析的结果,更新水位模型和实时监测系统。
# 举例:更新水位模型
updated_model = improve_model(model, observed_data, simulated_data)
5. 结果总结与建议:
- 报告生成和决策建议: 汇总历史数据分析的结果,生成报告,并提出关于模型校准、管理策略效果和系统改进的建议。
# 举例:生成报告
generate_report(model_evaluation, strategy_evaluation, sensitivity_analysis)
6. 实时监测与调整:
- 实时监测系统维护: 结合历史数据分析的结果,不断调整水位模型和管理策略,保持实时监测系统的准确性。
# 举例:实时调整策略
real_time_adjustment = adjust_strategy(real_time_data, model_parameters)
7. 决策支持系统的改进:
- 决策支持系统更新: 根据历史数据分析的结果,改进决策支持系统,提供更准确的实时水位管理建议。
# 举例:更新决策支持系统
updated_decision_support_system = improve_decision_support_system(old_system, new_data)
更多内容具体可以看看我的下方名片!里面包含有美赛一手资料与分析!
另外在赛中,我们也会持续陪大家一起解析美赛的一些方向
关注 CS数模 团队,数模不迷路~
相关文章:

2024年美赛 (D题ICM)| 湖流网络水位控制 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。 让我们来看看美赛的D题! 完整内容可以在文章末尾领…...
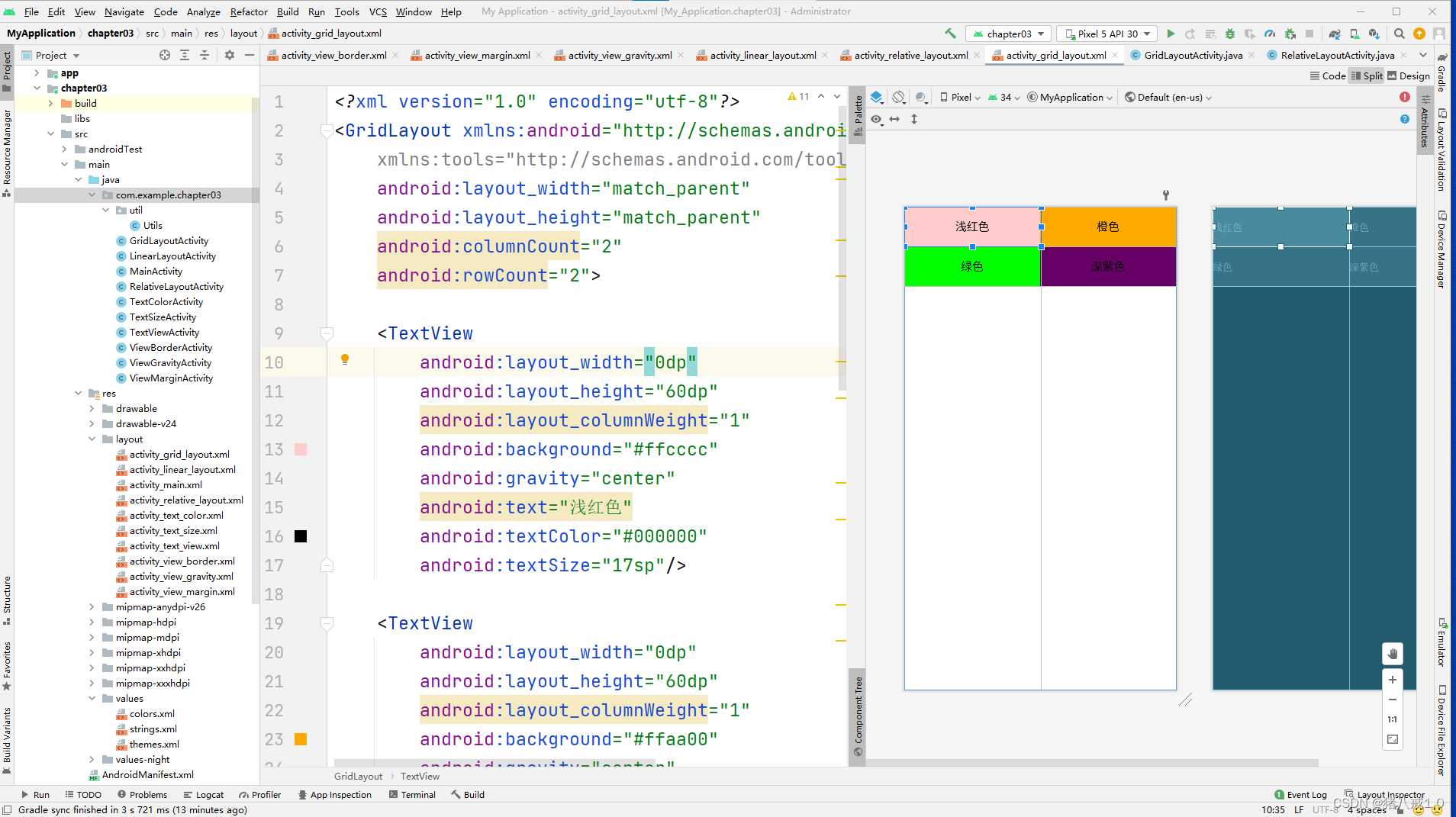
安卓网格布局GridLayout
<?xml version"1.0" encoding"utf-8"?> <GridLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:tools"http://schemas.android.com/tools"android:layout_width"match_parent"android:la…...
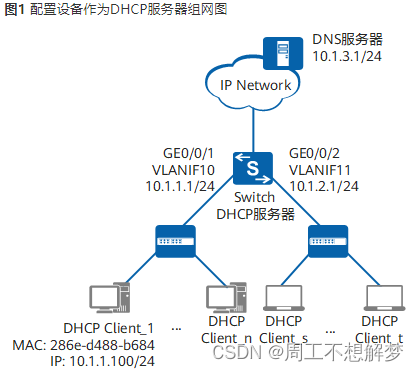
DHCP简介
定义 动态主机配置协议DHCP(Dynamic Host Configuration Protocol)是一种用于集中对用户IP地址进行动态管理和配置的技术。即使规模较小的网络,通过DHCP也可以使后续增加网络设备变得简单快捷。 DHCP是在BOOTP(BOOTstrap Protoc…...

Hadoop生态系统中一些关键组件的详细解析
1. Hadoop核心组件 HDFS(Hadoop Distributed File System): 分布式文件存储系统。提供高吞吐量的数据访问,非常适合用于大规模数据集。有高容错性,通过在多个节点间复制数据块来实现。 MapReduce: 一种编程模型,用于在…...

功能强大的开源数据中台系统 DataCap 2024.01.1 发布
推荐一套基于 SpringBoot 开发的简单、易用的开源权限管理平台,建议下载使用: https://github.com/devlive-community/authx 推荐一套为 Java 开发人员提供方便易用的 SDK 来与目前提供服务的的 Open AI 进行交互组件:https://github.com/devlive-commun…...
Redis的bitmap使用不当,我内存爆了
背景 最近发现Redis的内存持续暴涨, 涨的有点吓人,机器都快扛不住了,不得不进行Redis内存可视化分析,发现大量的String类型的大key 经分析,最近上线了页面UV的统计,那目前如何做的呢? 通过访…...

基于python的新闻爬虫
咱们这个任务啊,就是要从一个指定的网站上,抓取新闻内容,然后把它们整整齐齐地保存到本地。具体来说,就是要去光明网的板块里,瞅瞅里面的新闻,把它们一条条地保存下来。 首先,咱得有个网址&…...

C#基础题
值类型和引用类型之间的区别是什么? 值类型在内存中存储实际值,而引用类型存储对对象的引用。值类型在栈上分配内存,而引用类型在堆上分配内存。值类型是不可变的,而引用类型是可变的。值类型的大小是固定的,而引用类型…...
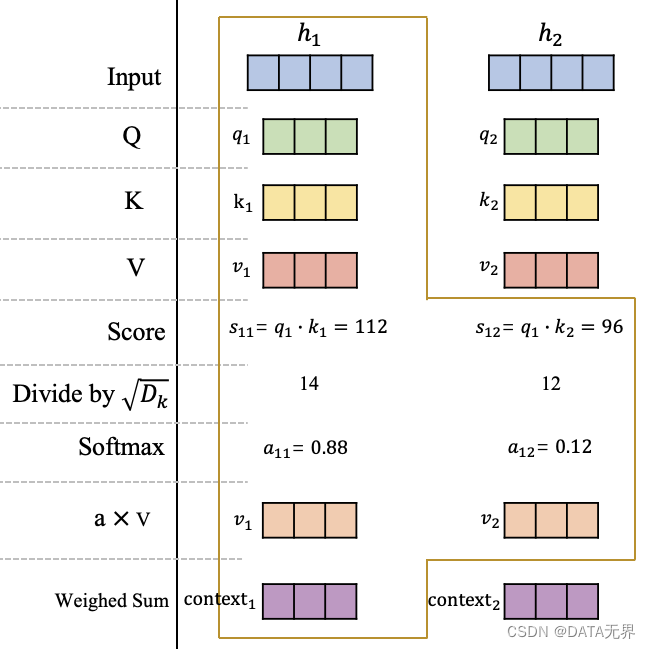
AI大语言模型学习笔记之三:协同深度学习的黑魔法 - GPU与Transformer模型
Transformer模型的崛起标志着人类在自然语言处理(NLP)和其他序列建模任务中取得了显著的突破性进展,而这一成就离不开GPU(图形处理单元)在深度学习中的高效率协同计算和处理。 Transformer模型是由Vaswani等人在2017年…...
c++阶梯之auto关键字与范围for
auto关键字(c11) 1. auto关键字的诞生背景 随着程序的逐渐复杂,程序代码中用到的类型也越来越复杂。譬如: 类型难以拼写;含义不明确容易出错。 比如下面一段代码: #include <string> #include &…...

第八篇:node模版引擎Handlebars及他的高级用法(动态参数)
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 📘 引言: …...

css3 属性 backface-visibility 的实践应用
backface-visibility 是一个用于控制元素在面对屏幕不同方向时的可见性的CSS3特性。它有两个可能的值: visible:当元素不面向屏幕(即背面朝向用户)时,元素的内容是可以被看到的。hidden:当元素不面向屏幕…...

嵌入式学习第十七天
C语言小项目: 制作俄罗斯方块小游戏(全部) 主函数部分 #include <stdio.h> #include <unistd.h> #include <string.h> #include <signal.h> #include <stdlib.h> #include <time.h> #include "b…...
使用Python的Turtle模块简单绘制烟花效果
import turtle import random# 初始化屏幕 screen turtle.Screen() screen.bgcolor("black") screen.title("烟花模拟")# 创建一个Turtle来绘制烟花 firework turtle.Turtle() firework.hideturtle() firework.speed(0) # 设置绘图速度为最快# 绘制烟花…...

数学建模-退火算法和遗传算法
退火算法和遗传算法 一.退火算法 退火算法Matlab程序如下: [W]xlsread(D:100个目标经度纬度);>> x[W(:,1)];>> y[W(:,2)];>> w[x y];;d1[70, 40];>> w[d1;w;d1]ww*pi/180;%角度化成弧度dzeros(102);%距离矩阵初始化for i1:101…...

Qt开源版 vs 商业版 详细比较!!!!
简单整理Qt开源版与商业版有哪些差别,仅供参考。 简单对比 开源版商业版许可证大部分采用对商业使用不友好的LGPLv3具备商业许可证保护代码专有许可证相关大部分模块使用LGPLv3和部分模块使用GPL组成仅第三方开源组件使用Qt的其他许可证Qt模块功能支持支持技术支持…...

华为云CodeArts Snap荣获信通院优秀大模型案例及两项荣誉证书
2024年1月25日,中国人工智能产业发展联盟智能化软件工程工作组(AI for Software Engineering,下文简称AI4SE)在京召开首届“AI4SE创新巡航”活动。在活动上,华为云大模型辅助系统测试代码生成荣获“2023AI4SE银弹优秀案…...
)
小程序的应用、页面、组件生命周期(超全版)
小程序生命周期 应用的生命周期 onLaunch: 初始化小程序完成时触发,且全局只触发一次; onShow: 小程序初始化完成(启动)或从后台切换到前台显示时触发; onHide: 小程序从前台切换到后台隐藏时触发(如切换…...
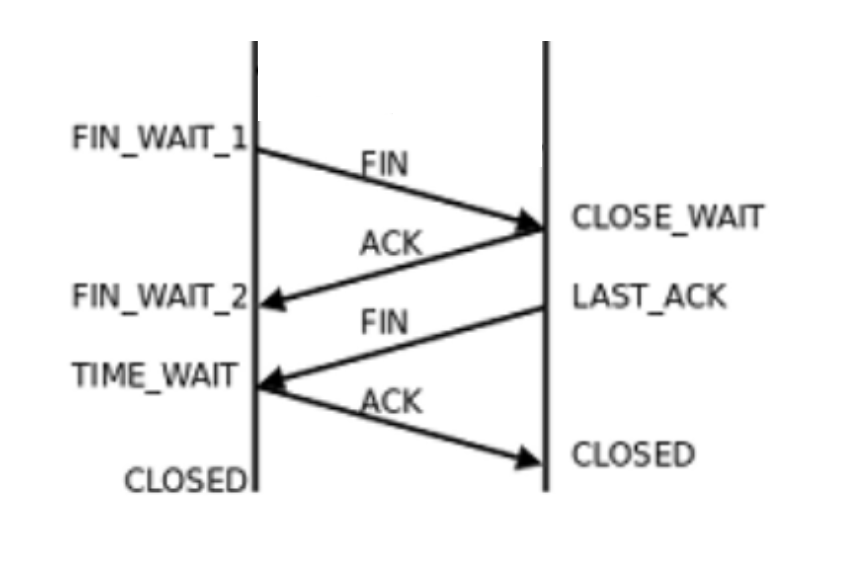
TCP四次握手
TCP 协议在关闭连接时,需要进行四次挥手的过程,主要是为了确保客户端和服务器都能正确地关闭连接。 # 执行流程 四次挥手的具体流程如下: 客户端发送 FIN 包:客户端发送一个 FIN 包,其中 FIN 标识位为 1,…...
EBC金融英国CEO:高波动性周期下,如何寻找市场的稳定性?
利率主导的市场,将在2024年延续。目前,固收市场对于降息的定价,正通过利率传导至不同资产中。尽管市场迫切利用通胀去佐证降息,但各国央行仍囿于通胀目标的政策桎梏。政策和市场预期的博弈将继续牵动市场脉搏,引发价格…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
