C语言-算法-最短路
【模板】Floyd
题目描述
给出一张由 n n n 个点 m m m 条边组成的无向图。
求出所有点对 ( i , j ) (i,j) (i,j) 之间的最短路径。
输入格式
第一行为两个整数 n , m n,m n,m,分别代表点的个数和边的条数。
接下来 m m m 行,每行三个整数 u , v , w u,v,w u,v,w,代表 u , v u,v u,v 之间存在一条边权为 w w w 的边。
输出格式
输出 n n n 行每行 n n n 个整数。
第 i i i 行的第 j j j 个整数代表从 i i i 到 j j j 的最短路径。
样例 #1
样例输入 #1
4 4
1 2 1
2 3 1
3 4 1
4 1 1
样例输出 #1
0 1 2 1
1 0 1 2
2 1 0 1
1 2 1 0
提示
对于 100 % 100\% 100% 的数据, n ≤ 100 n \le 100 n≤100, m ≤ 4500 m \le 4500 m≤4500,任意一条边的权值 w w w 是正整数且 1 ⩽ w ⩽ 1000 1 \leqslant w \leqslant 1000 1⩽w⩽1000。
数据中可能存在重边。
代码实现
#include <stdio.h>
void floyd(); // Floyd算法
#define MAX 10000
#define INF 0x3f3f3f3f // 无穷大
int n, m;
int g[MAX][MAX];int main()
{int i, j, u, v, w;scanf("%d %d", &n, &m); // 输入点的个数和边的条数for (i = 1; i <= n; i++) // 初始化图的邻接矩阵{for (j = 1; j <= n; j++){// 对角线上的元素为0,其他元素为无穷大if (i == j){g[i][j] = 0;}else{g[i][j] = INF;}}}for (i = 0; i < m; i++){scanf("%d %d %d", &u, &v, &w);if (g[u][v] > w) // 由于可能存在重边,我们需要保留权值最小的那条边{g[u][v] = w;g[v][u] = w;}}floyd(); // 执行Floyd算法for (i = 1; i <= n; i++){for (j = 1; j <= n; j++){printf("%d ", g[i][j]); }printf("\n");}return 0;
}void floyd()
{int i, j, k; // i和j是起始和结束节点,k是中间节点for (k = 1; k <= n; k++){for (i = 1; i <= n; i++){for (j = 1; j <= n; j++){// 如果通过k节点的路径比当前i到j的路径短,那么更新g[i][j]if (g[i][k] != INF && g[k][j] != INF && g[i][j] > g[i][k] + g[k][j]){g[i][j] = g[i][k] + g[k][j];}}}}
}
无向图的最小环问题
题目描述
给定一张无向图,求图中一个至少包含 3 3 3 个点的环,环上的节点不重复,并且环上的边的长度之和最小。该问题称为无向图的最小环问题。在本题中,你需要输出最小的环的边权和。若无解,输出 No solution.。
输入格式
第一行两个正整数 n , m n,m n,m 表示点数和边数。
接下来 m m m 行,每行三个正整数 u , v , d u,v,d u,v,d,表示节点 u , v u,v u,v 之间有一条长度为 d d d 的边。
输出格式
输出边权和最小的环的边权和。若无解,输出 No solution.。
样例 #1
样例输入 #1
5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20
样例输出 #1
61
提示
样例解释:一种可行的方案: 1 − 3 − 5 − 2 − 1 1-3-5-2-1 1−3−5−2−1。
对于 20 % 20\% 20% 的数据, n , m ≤ 10 n,m \leq 10 n,m≤10。
对于 60 % 60\% 60% 的数据, m ≤ 100 m\leq 100 m≤100。
对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 100 1\le n\leq 100 1≤n≤100, 1 ≤ m ≤ 5 × 1 0 3 1\le m\leq 5\times 10^3 1≤m≤5×103, 1 ≤ d ≤ 1 0 5 1 \leq d \leq 10^5 1≤d≤105。
无解输出包括句号。
代码
相关文章:

C语言-算法-最短路
【模板】Floyd 题目描述 给出一张由 n n n 个点 m m m 条边组成的无向图。 求出所有点对 ( i , j ) (i,j) (i,j) 之间的最短路径。 输入格式 第一行为两个整数 n , m n,m n,m,分别代表点的个数和边的条数。 接下来 m m m 行,每行三个整数 u …...

【操作系统·考研】I/O管理概述
1.I/O设备 1.1 块设备 信息交换以数据块为单位,它属于有结构设备。 块设备传输速率较高,可寻址,且可对该设备随机地的读写。 栗子🌰:磁盘。 1.2 字符设备 信息交换以字符为单位,属于无结构类型。 字符…...
Linux实验记录:使用vsftpd服务传输文件
前言: 本文是一篇关于Linux系统初学者的实验记录。 参考书籍:《Linux就该这么学》 实验环境: VmwareWorkStation 17——虚拟机软件 RedHatEnterpriseLinux[RHEL]8——红帽操作系统 备注: 为了解决在多样复杂的设备之间解决传…...

实习|基于SSM的实习管理系统设计与实现(源码+数据库+文档)
实习管理系统目录 目录 基于SSM的实习管理系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、管理员功能介绍 (1)管理员登录 (2)实训方向管理 (3)公告信息管理 (4࿰…...
商品介绍和规则参数图片映射和IP设置
虚拟路径映射配置: registry.addResourceHandler("/image/productIntroImgs/**").addResourceLocations("file:D:\\java1234-mall-v3\\productIntroImgs\\");registry.addResourceHandler("/image/productParaImgs/**").addResourceL…...

【React】前端React 代码中预览展示excel文件
封装了ExcelView来展示excel文件,支持显示loading 1.安装依赖 npm i js-preview/excel源码 import React, { useEffect, useRef, useState } from react import jsPreviewExcel, { JsExcelPreview } from js-preview/excel import js-preview/excel/lib/index.cs…...
QButtonGroup使用介绍
一、简介 QButtonGroup是PyQt5库中的一个组件,主要用于组织和管理一组按钮。通过QButtonGroup,可以方便地实现单选框或多选框功能,统一处理按钮的信号,并且可以为按钮分组设定ID以进行识别。 1、原始工程 from PyQt5.Qt import …...
最近nvm安装报错的原因找到了——npm原淘宝镜像正式到期!
前言 📫 大家好,我是南木元元,热爱技术和分享,欢迎大家交流,一起学习进步! 🍅 个人主页:南木元元 目录 背景 错误原因 问题排查 淘宝镜像 证书到期 问题解决 结语 背景 我们…...

docker面试问题二
如何防止Docker容器中的漏洞和攻击? 防止Docker容器中的漏洞和攻击是一个多层次、多方面的任务,涉及从镜像构建、容器运行到网络安全的整个生命周期。以下是一些关键措施: 使用官方和受信任的镜像: 总是从官方源或受信任的第三方…...

嵌入式中C 语言中的三块技术难点
C 语言在嵌入式学习中是必备的知识,甚至大部分操作系统都要围绕 C 语言进行,而其中有三块技术难点,几乎是公认级别的“难啃的硬骨头”。 今天就来带你将这三块硬骨头细细拆解开来,一定让你看明白了。 0x01 指针 指针是公认最难理…...
基于SSM的个性化旅游攻略定制系统设计与实现(有报告)。Javaee项目。ssm项目。
演示视频: 基于SSM的个性化旅游攻略定制系统设计与实现(有报告)。Javaee项目。ssm项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构…...
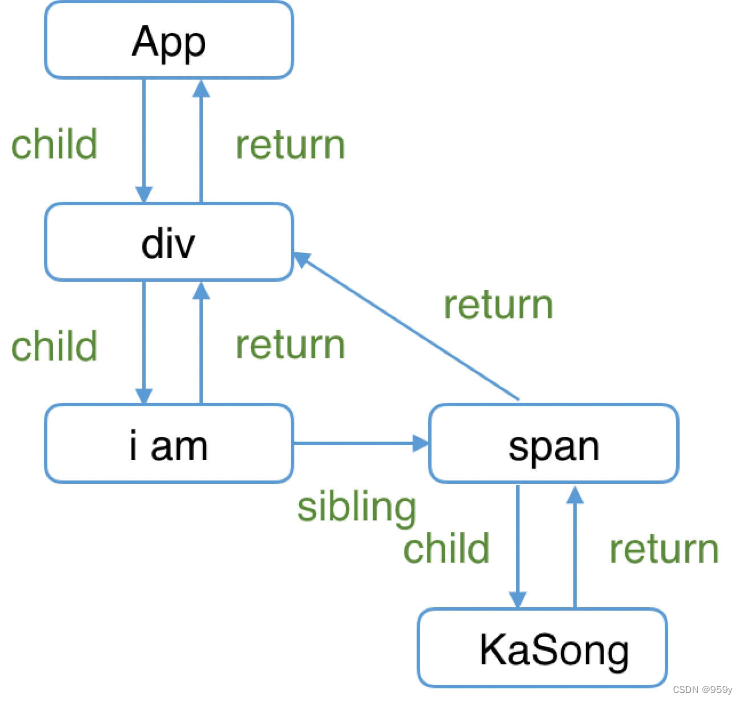
[React源码解析] Fiber (二)
在React15及以前, Reconciler采用递归的方式创建虚拟Dom, 但是递归过程不可以中断, 如果组件的层级比较深的话, 递归会占用线程很多时间, 那么会造成卡顿。 为了解决这个问题, React16将递归的无法中断的更新重构为异步的可中断更新, Fiber架构诞生。 文章目录 1.Fiber的结构2…...
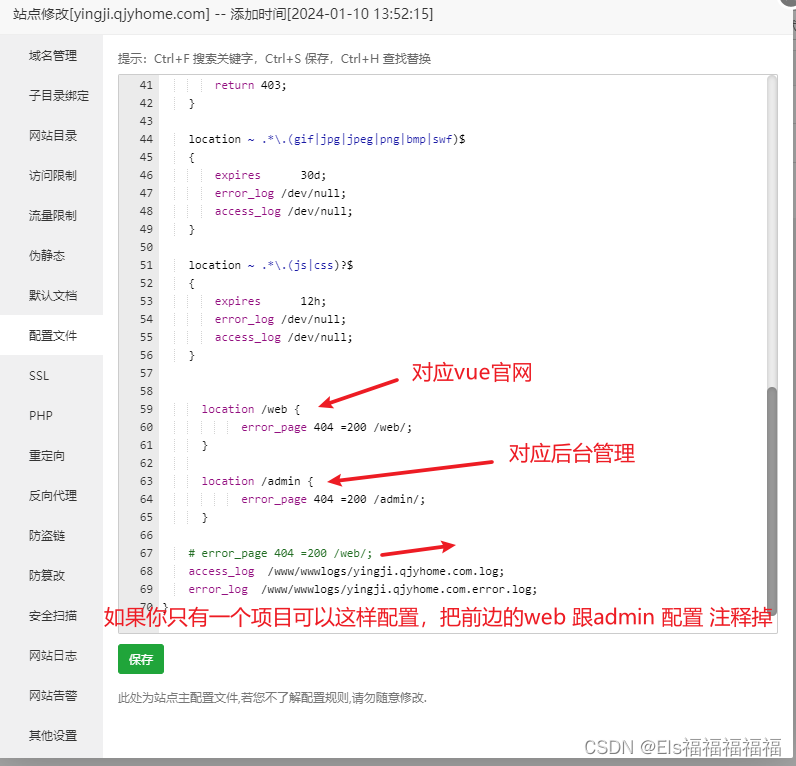
Nginx 多项目部署,vue刷新404 解决方案
网上找的资料大多都解决不了,废话不多说直接告诉你解决方法。 环境是 TP6 VUE前端官网 VUE 后台管理 部署 两个项目 刷新 404 解决方案 Nginx 配置 直接贴图 如果解决了,给我顶起来,让更多人 快速的解决。...
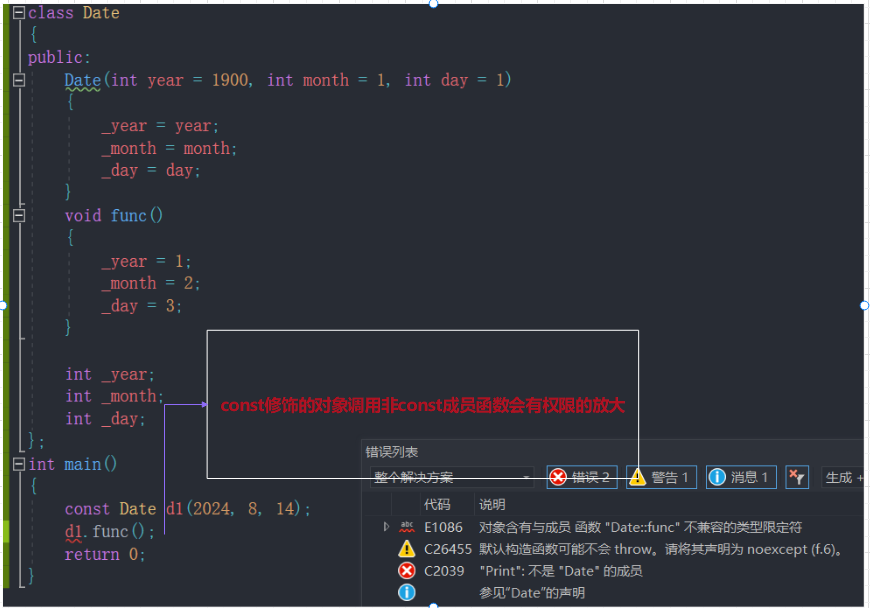
[C++]类和对象(中)
一:类的六个默认成员函数 如果一个类中什么成员都没有,简称为空类。空类中并不是什么都没有,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。默认成员函数:用户没有显式实现,编译器会生成的成员函数称为…...
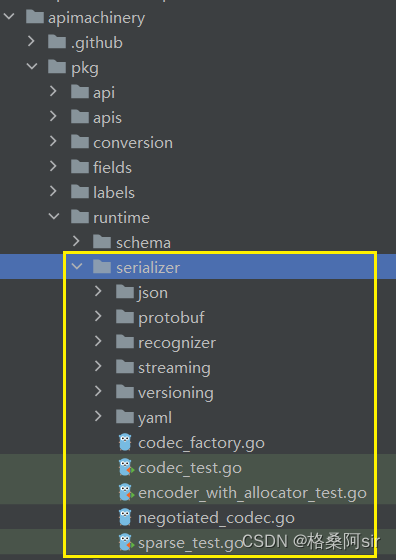
Kubernetes operator(五)api 和 apimachinery 篇
云原生学习路线导航页(持续更新中) 本文是 Kubernetes operator学习 系列第五篇,主要对 k8s.io/api 和 k8s.io/apimachinery 两个项目 进行学习基于 kubernetes v1.24.0 代码分析Kubernetes operator学习系列 快捷链接 Kubernetes operator&a…...

接口自动化测试中解决接口间数据依赖
在实际的测试工作中,在做接口自动化测试时往往会遇到接口间数据依赖问题,即API_03的请求参数来源于API_02的响应数据,API_02的请求参数又来源于API_01的响应数据。 因此通过自动化方式测试API_03接口时,需要预先请求API_02接口&a…...
)
七、测试计划(软件工程)
1.引言 1.1编写目的 1.2项目背景 1.3定义 1.4参考资料 2.任务概述 2.1目标 2.2运行环境 2.3需求概述 2.4条件与限制 3.计划 3.1测试方案 3.2测试项目 3.3测试准备 3.4测试机构及人员 4.测试项目说明…...
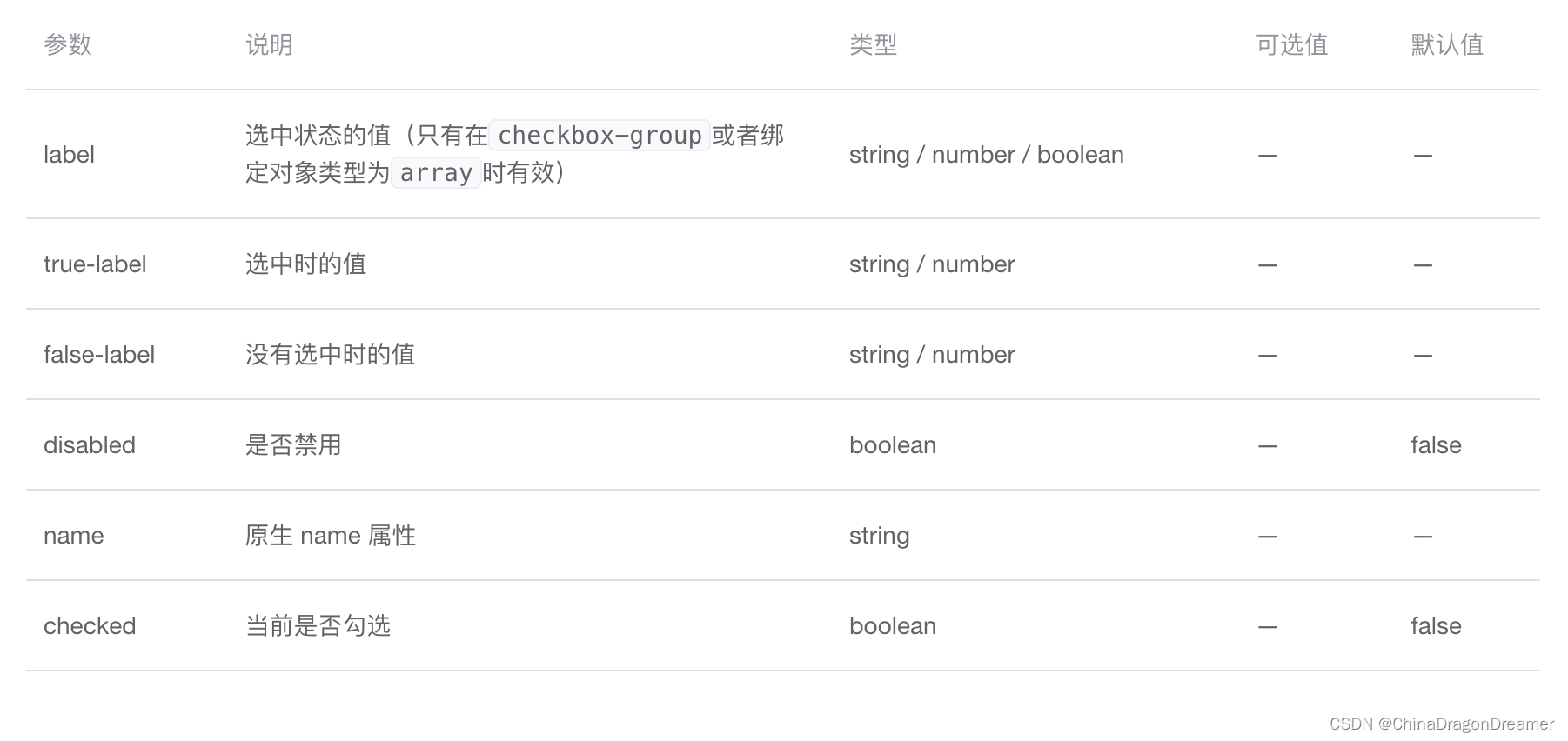
ElementUI Form:Checkbox 多选框
ElementUI安装与使用指南 Checkbox 多选框 点击下载learnelementuispringboot项目源码 效果图 el-checkbox.vue (Checkbox 多选框)页面效果图 项目里el-checkbox.vue代码 <script> const cityOptions [上海, 北京, 广州, 深圳] export def…...

如何统一监听Vue组件报错
window.onerror 全局监听所有JS错误,包括异步错误但是它是JS级别的,识别不了Vue组件信息,Vue内部的错误还是用Vue来监听捕捉一些Vue监听不到的错误 errorCaptured生命周期 监听所有下级组件的错误返回false会阻止向上传播到window.onerror …...
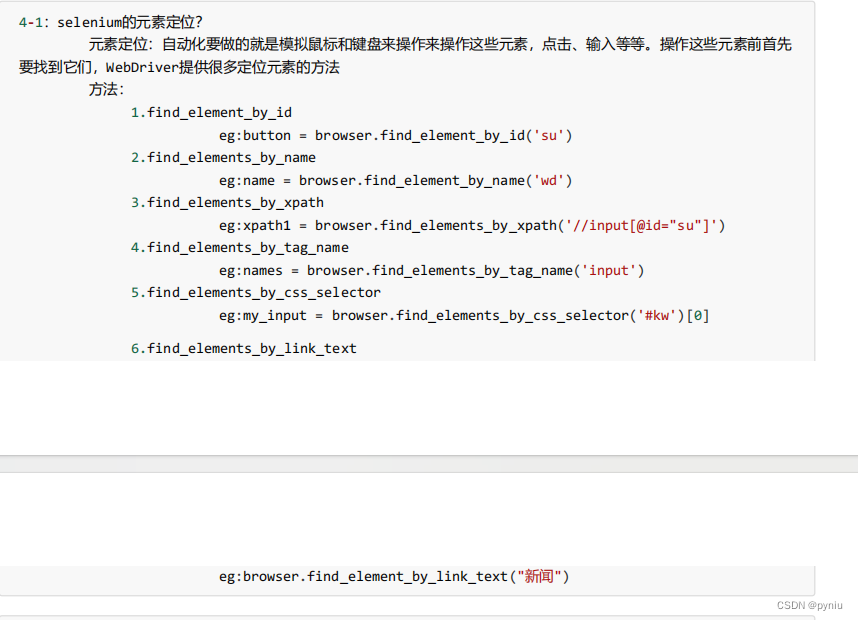
python爬虫4
#1.练习 # (1) 获取网页的源码 # (2) 解析 解析的服务器响应的文件 etree.HTML # (3) 打印 import urllib.request urlhttps://www.baidu.com/ headers {User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
