【数据结构】分治策略
现场保护和现场恢复
文章目录
- 分治策略
- 分治法解决问题有以下四个特征:
- 分治法步骤:
- 递归:
- 解决以下问题:
- 倒序输出整数
- 求最大公约数(递归和非递归)
- 菲波那切数列
不要尝试间接
要使用直接递归(自己调用自己)
分治策略
分治法解决问题有以下四个特征:
- 该问题的规模小到一定程度就容易解决。
- 把大问题分解成小问题,是将问题的规模变小,而不是将问题变小
- 使用小规模的解,可以合并,该问题原规模的解
- 该问题所分解的各个子模块是相互独立的。
分治法步骤:
在分治策略中递归地求解一个问题,在每层递归中有如下解决步骤:
分解:递归地求解子问题,子问题地形式与原问题一样,只是规模更小。
解决:递归地求解子问题,如果子问题地规模足够小,则停止递归,直接求解
合并:将小规模地解组合成原规模地解
递归函数分为 递推和递归两个过程
每当调用发生:就要分配新的栈帧(形参数据,现场保护,局部变量);而与普通函数调用不同,由于递推是一个逐层调用的过程,因此存在一个连续的分配栈帧的过程,直至遇到递归终止条件时,才开始回归,这时才会释放栈帧空间,返回到上一层,直到返回到主调函数。
- 简单的函数调用过程:

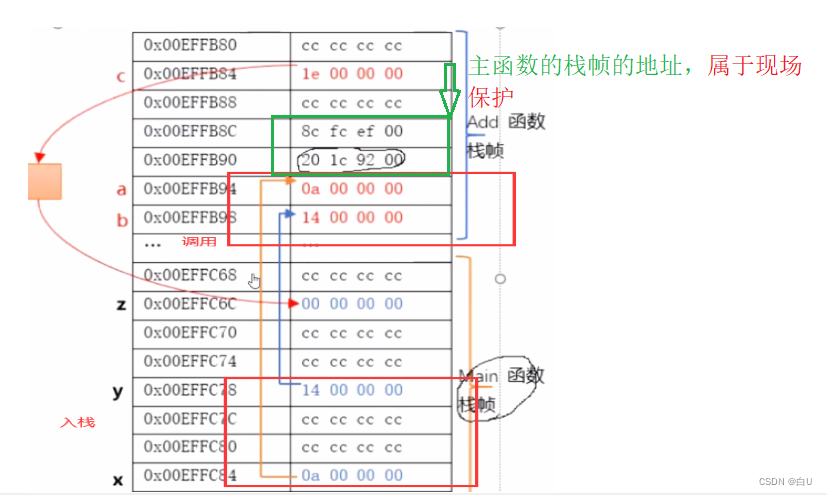
递归:
空间复杂程度位S(n),每次都要开辟栈帧
必要的情况才使用递归(如树形)
不存在死递归的概念(因为栈帧基本就1M,不断开辟栈帧,资源就损耗完了)
循环占用的cpu资源。因此存在死循环。

解决以下问题:

下面程序:
倒序输出整数
Print(int n ){if(n != 0){ ----->printf("%d ",n%10); 5,4,3,2,1Print(n/10); 1235123121 0 开始回归printf("%d ",n%10);Print(n/10); printf("%d ",n%10);1,2,3,4,5<----}return;}
求最大公约数(递归和非递归)
int fun(int a, int b)
{ //求最大公约数if (b != 0) //退出递归的条件{return fun(b,a%b); } return a;}
int fun1(int a, int b)
{ //求最大公约数while (b != 0) {int c = a%b;a = b;b = c;} return a
}

错误1:
菲波那切数列
后一个数为前两个之和。
打印:
int main()
{const int n = 10;int arr[n] = {1,1};for(int i =2;i<n;i++){arr[i] = arr[i-1]+arr[i-2];}
}
非递归:
int fac(int n)
{int a = 1,b=1,c=1; //当n<=3的时候,打印的值均为1也就是前两位for(int i = 3;i<=n;i++){c = a+b;a = bb =c;}return c;
}
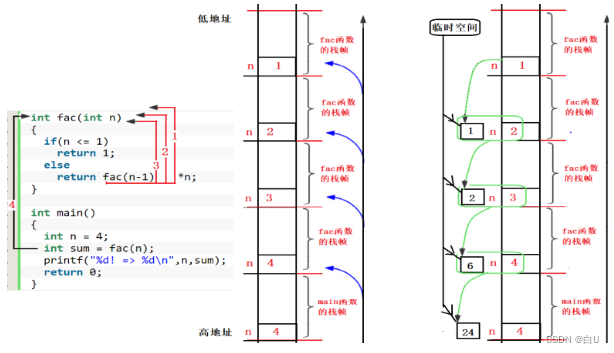
递归:
时间复杂程度:2^n ,跑法是一颗二叉树。
空间复杂程度最大深度是S(n) 。因为递推时开辟栈帧,回归时,销毁栈帧
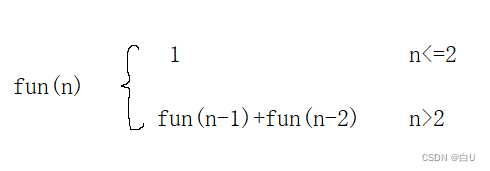
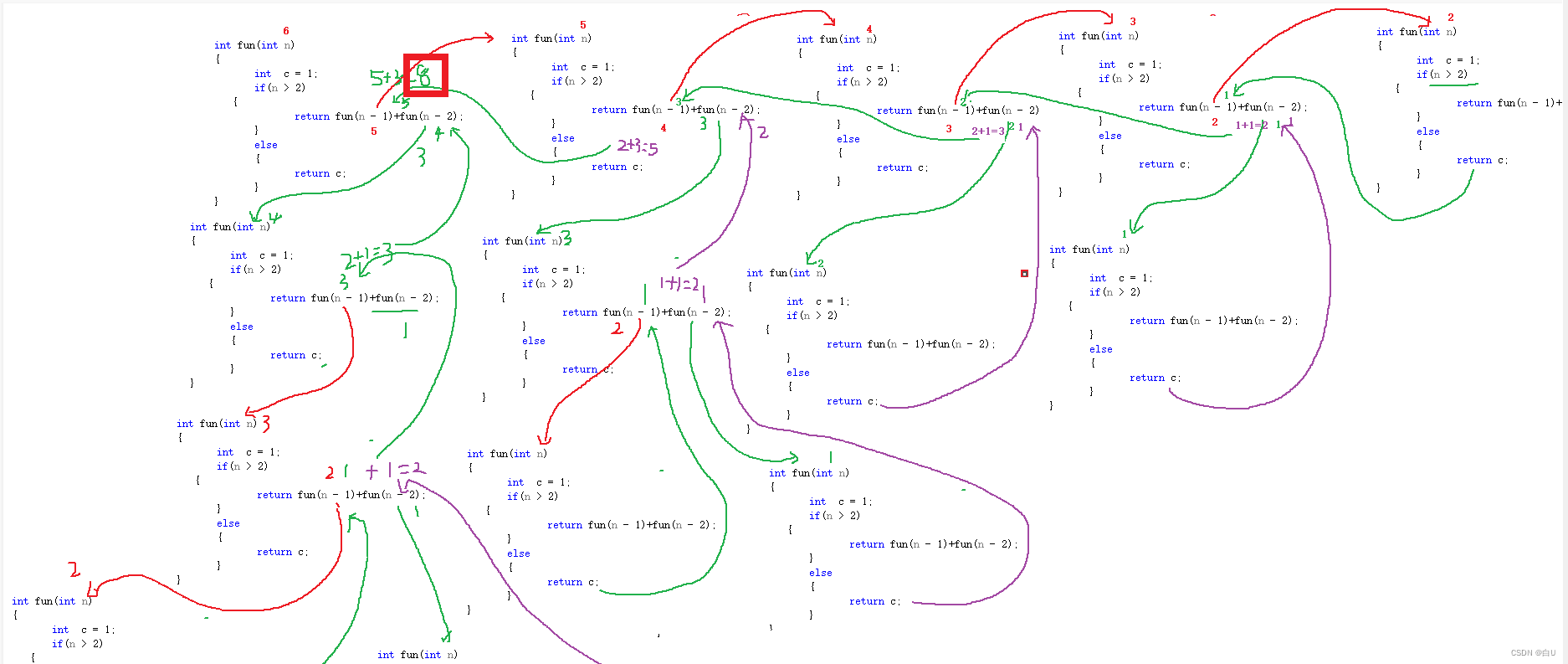
1.判断退出条件
2.分析最后需要的结果
int fac(int n)
{int c = 1;if(n > 2){return fun(n - 1)+fun(n - 2);}else{return c;}}

查询:递归和非递归(边界检查)
递归
int FindValue(int* br, int n, int val)
{//assertint pos = n-1;if(pos >= 0 && br[pos] != val ){return FindValue(br,pos,val);}return pos;
}
非递归
int FindValue(int* br, int n, int val)
{//assertint pos = n-1;if(pos >= 0 && br[pos] != val ){pos++;}return pos;
}
递归:
int FindValue(int* br, int n, int val)
{//assert//n<1 比 n<=0要好,因为这里的n是规模,1—n的数,而<=0,又有下标的含义if (n < 1&& br[n-1] != val){return n-1;}return FindValue(br, n-1, val);
}
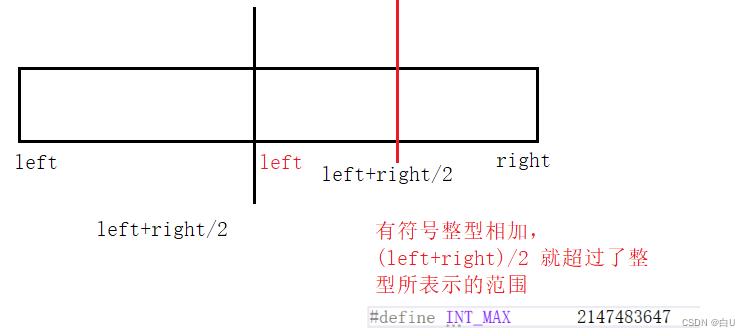
二分查询:(要求数据是有序的,并且数据在内存中的存储是连续的)
如果数据量小不用考虑下面问题,数据量大,必须考虑下面问题。
所以采用(right-left)/2 + left
例如 1,2,3,4,5 ,6,7,8,9 (8-0)/2 = 4 4+0 = 4,即4号下标
由于存放是以2进制存放,所以左移一位,就相当于除以二
((right-left)>> 1) +left
int BinaryFind_Value(int *br,int len,int val)
{//assertint left = 0, right = len - 1;int pos = -1;int mid = -1;while (left < right){ //如果是left+right/2mid = (right - left) / 2 + left;//(right - left) >>1 + left;if (br[mid] < val){left = mid + 1;}else if(br[mid] > val){right = mid; //mid不能加一,因为left<right//加一有最右边的元素访问不到。}else{pos = mid;break;}}return pos;
}
- int ar[] = {11 ,11, 11, 11, 11, 11, 12, 12, 13, 14, 15}
查最左边的11
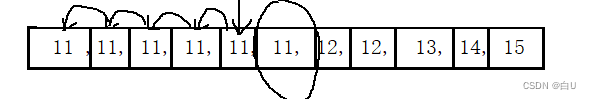
int BinaryFind_Value(int* br, int len, int val)
{//assertint left = 0, right = len - 1;int pos = -1;int mid = -1;while (left <= right){ //如果是left+right/2mid = (right - left) / 2 + left;//(right - left) >>1 + left;if (br[mid] < val){left = mid + 1;}else if (br[mid] > val){right = mid - 1; //mid不能加一,因为left<right//加一有最右边的元素访问不到。}else{ //可以比较下一个标的值while (mid > left && br[mid -1 ] == val){//pos = mid; 每次都赋值,浪费时间mid--;}pos = mid;break;}}return pos;
}
求ar[1,2,3,]所有子集
ar[0,0,0,0]
0,0,0,1
0,0,1,0
0,0,1,1
…
1,1,1,1
如何降时间复杂程度?
相关文章:
【数据结构】分治策略
现场保护和现场恢复 文章目录 分治策略分治法解决问题有以下四个特征:分治法步骤: 递归:解决以下问题:倒序输出整数求最大公约数(递归和非递归)菲波那切数列 不要尝试间接 要使用直接递归(自己调用自己&am…...
【PLC一体机】PLC一体机中如何实现触摸屏和PC电脑的通讯
博主今天准备把之前买的PLC一体机拿出来玩一下,翻看以前的博文,发现没有记录分享PLC一体机中如何实现触摸屏程序下载的内容。 如之前博文介绍的那样,PLC一体机由PLC和触摸屏两部分集成的设备,因此设备内部已经做好了PLC和触摸屏之…...

如何保证订单异步回调的幂等性
保证订单异步回调的幂等性是非常重要的,因为异步通知可能会由于网络问题、支付系统重试或其他原因导致多次发送同一个支付结果通知。以下是一些保证订单异步回调幂等性的常用方法: 接口设计幂等性: 在设计异步通知的接口时,考虑让…...
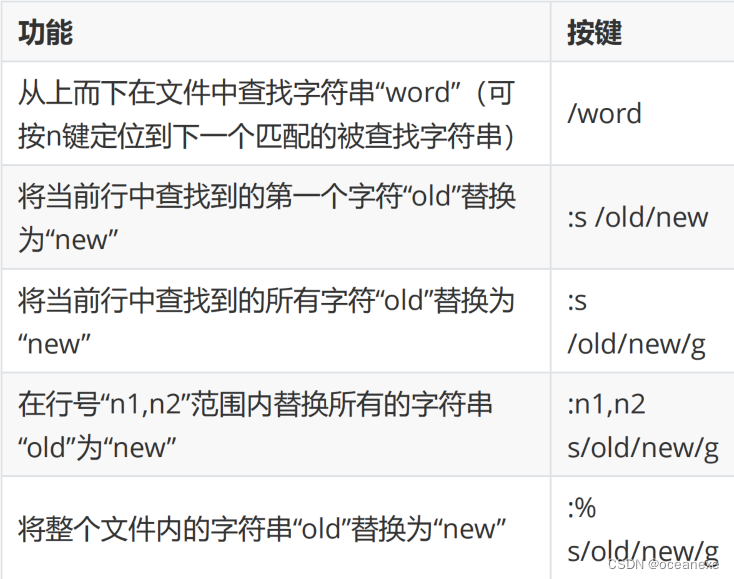
Linux下vim命令详解
vim #创建或编辑新的文件 #这将在当前目录下创建一个名为fi.txt的新文本文件。如果文件已经存在,将会编辑现有文件。 [rootsever ~]#vim fi.txt #对于普通的文本编辑操作,可以使用以下键盘命令: - i:进入插入模式ÿ…...
机器学习6-逻辑回归
逻辑回归是机器学习中一种常用于二分类问题的监督学习算法。虽然名字中包含“回归”,但实际上它用于分类任务,特别是对于输出为两个类别的情况。逻辑回归通过使用 logistic 函数将输入映射到一个在0,1范围内的概率值,然后根据这个概率值进行分类。 以下是逻辑回归的基本概念…...

关于Clone
关于Clone 一般情况下,如果使用clone()方法,则需满足以下条件。 1、对任何对象o,都有o.clone() ! o。换言之,克隆对象与原型对象不是同一个对象。 2、对任何对象o,都有o.clone().getClass() o.getClass()。换言之&a…...

【C++入门学习指南】:函数重载提升代码清晰度与灵活性
🎥 屿小夏 : 个人主页 🔥个人专栏 : C入门到进阶 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一、函数重载1.1 函数重载的概念1.2 函数重载的作用1.3 C支持函数重载的原理1.4 扩展 &…...
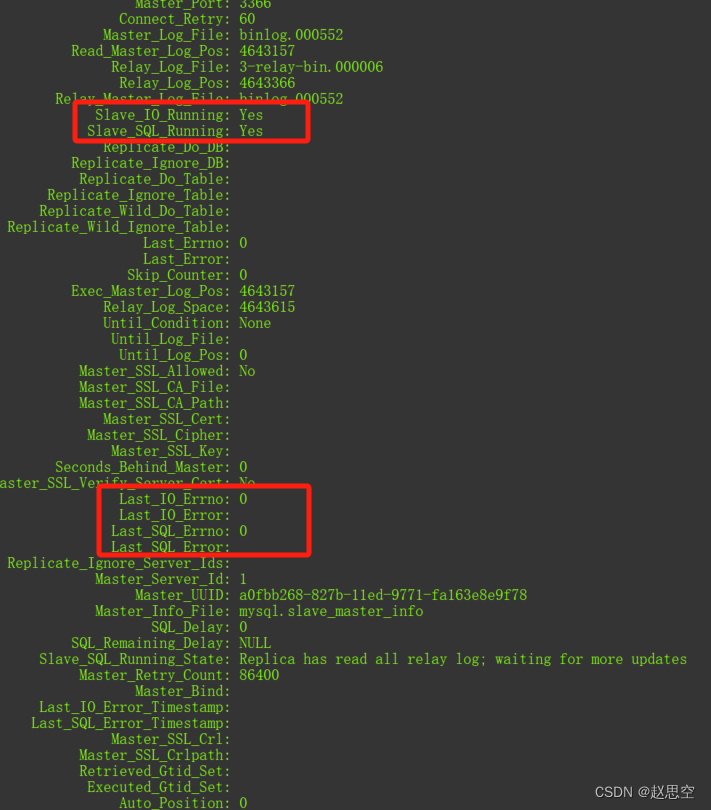
MySql主从同步,同步SQL_ERROR 1032解决办法
1.登录从库 mysql -u root -p 2.输入命令查看状态 SHOW SLAVE STATUS\G; 3.找到对应的错误数据位置 Slave_IO_Running: YesSlave_SQL_Running: NoReplicate_Do_DB: app_push_centerReplicate_Ignore_DB: Replicate_Do_Table: Replicate_Ignore_Table: Replicate_Wild_Do_Tabl…...

Webpack的性能优化
减少构建时间:使用webpack的缓存功能,通过配置cache: true来利用缓存,减少重复构建时间。 使用多线程或并行构建,可以利用webpack的parallel-webpack或HappyPack插件来实现。 充分利用硬件资源,例如利用多核CPU或者SSD…...
函数的详细介绍)
PyTorch中tensor.backward()函数的详细介绍
backward() 函数是PyTorch框架中自动求梯度功能的一部分,它负责执行反向传播算法以计算模型参数的梯度。由于PyTorch的源代码相当复杂且深度嵌入在C底层实现中,这里将提供一个高层次的概念性解释,并说明其使用方式而非详细的源代码实现。 在P…...

Linux 驱动开发基础知识——内核对设备树的处理与使用(十)
个人名片: 🦁作者简介:学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:Vir2021GKBS 🐼本文由…...

编程笔记 html5cssjs 077 Javascript 关键字
编程笔记 html5&css&js 077 Javascript 关键字 一、关键字二、Javascript关键字注意 在计算机编程语言中,关键字(Keyword)是指那些被编程语言赋予特殊含义、具有预定义用途的保留字。这些词汇不能用作变量名、函数名或其他标识符&…...
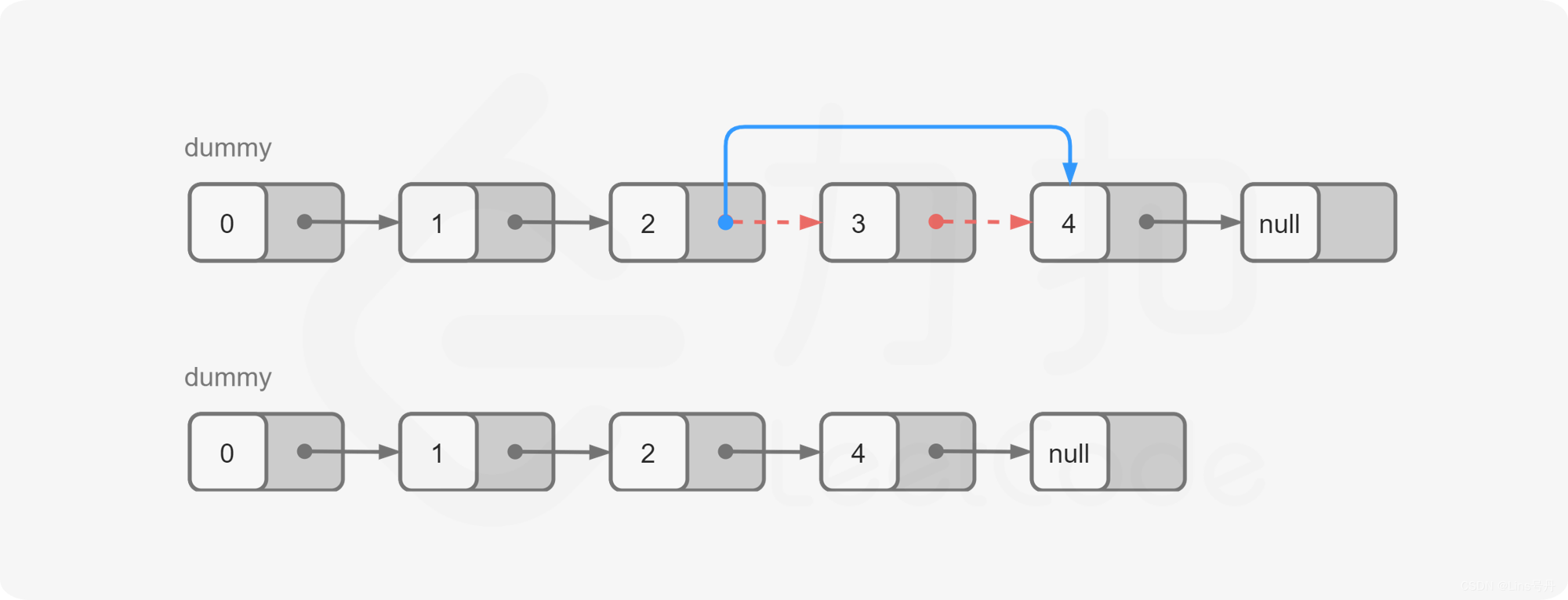
LeetCode_19_中等_删除链表的倒数第N个结点
文章目录 1. 题目2. 思路及代码实现(Python)2.1 计算链表长度2.2 栈 1. 题目 给你一个链表,删除链表的倒数第 n n n 个结点,并且返回链表的头结点。 示例 1: 输入: h e a d [ 1 , 2 , 3 , 4 , 5 ] , n…...

C++泛编程(3)
类模板基础 1.类模板的基本概念2.类模板的分文件编写3.类模板的嵌套 (未完待续...) 在往节内容中,我们详细介绍了函数模板,这节开始我们就来聊一聊类模板。C中,类的细节远比函数多,所以这个专题也会更复杂。…...
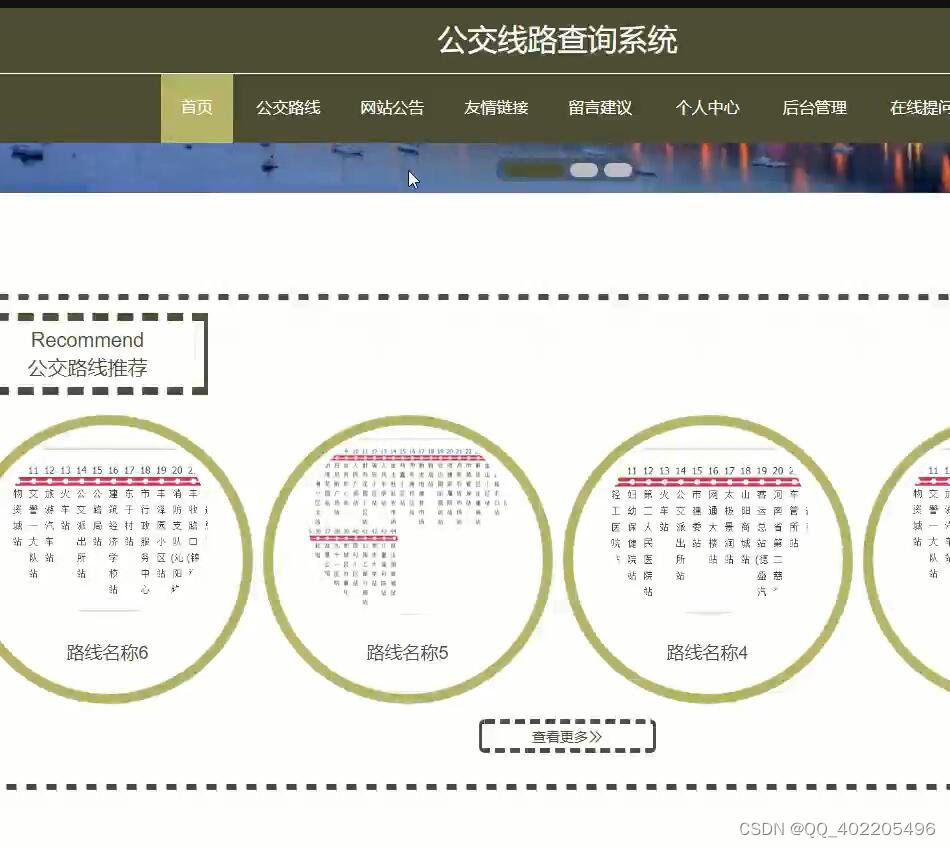
python基于django的公交线路查询系统mf383
1.个人信息的管理:对用户名,密码的增加、删除等 2.线路信息的管理:对线路的增加、修改、删除等 3.站点信息的管理:对站点的增加、修改、删除等 4.车次信息的管理:对车次的增加、修改、删除等 5.线路查询、站点查询 …...

ElementUI 组件:Container 布局容器实例
ElementUI安装与使用指南 Container 布局容器 点击下载learnelementuispringboot项目源码 效果图 el-container-example.vue(Container 布局容器实例)页面效果图 项目里el-container-example.vue代码 <script> export default {name: el_cont…...
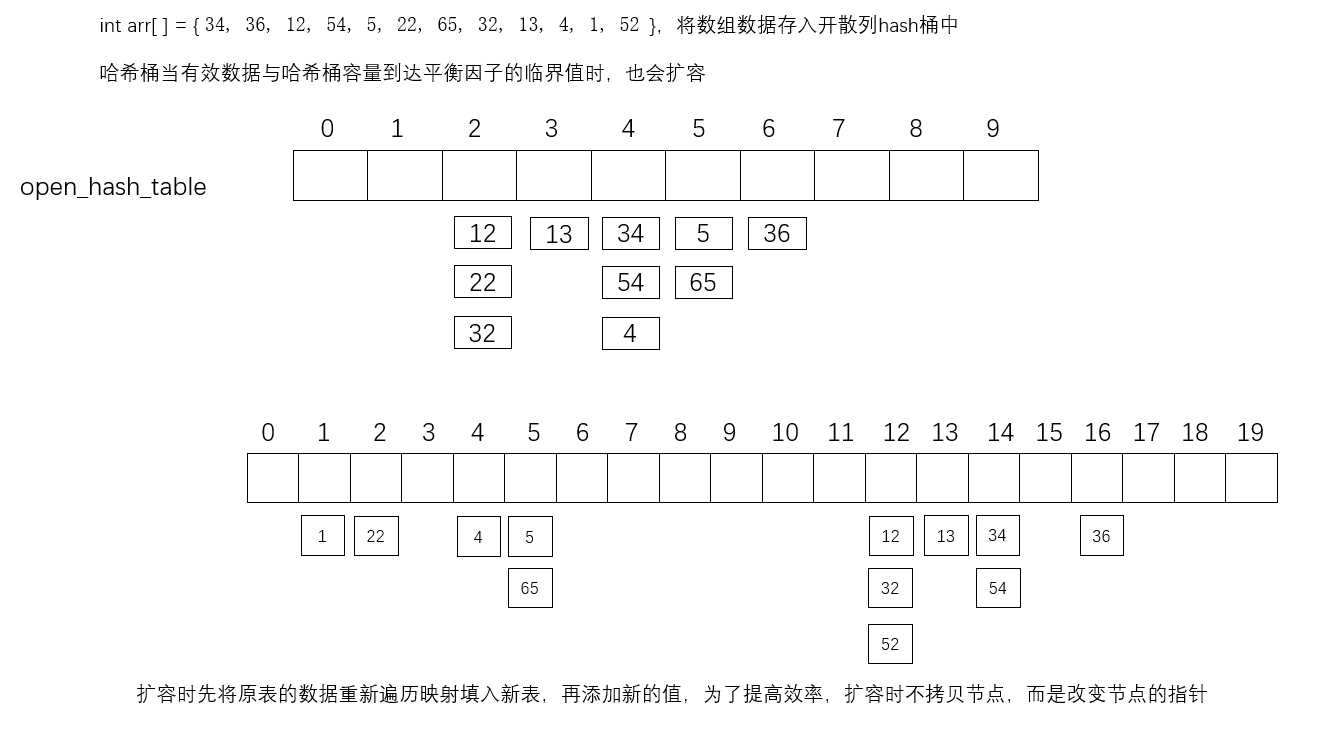
【数据结构 09】哈希
哈希算法:哈希也叫散列、映射,将任意长度的输入通过散列运算转化为固定长度的输出,该输出就是哈希值(散列值)。 哈希映射是一种压缩映射,通常情况下,散列值的空间远小于输入值的空间。 哈希运…...

理解和管理Linux文件权限
理解和管理Linux文件权限 文件权限的基本概念和表示方式 文件权限管理在Linux系统中是非常重要的,它决定了谁可以访问、读取、写入或执行文件。文件权限以及所有者、所属组等属性可以通过 ls -l 命令查看。 在 ls -l 命令的输出中,文件的权限通常表示…...

爬虫(二)
1.同步获取短视频 1.只要播放地址对Json数据解析,先把列表找出: 2.只想要所有的播放地址,通过列表表达式循环遍历这个列表拿到每个对象,再从一个个对象里面找到Video,再从Video里面找到播放地址(play_addr),再从播放地址找到播放…...
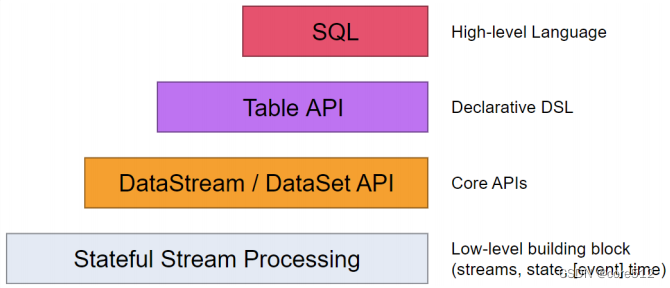
Flink实战四_TableAPISQL
接上文:Flink实战三_时间语义 1、Table API和SQL是什么? 接下来理解下Flink的整个客户端API体系,Flink为流式/批量处理应用程序提供了不同级别的抽象: 这四层API是一个依次向上支撑的关系。 Flink API 最底层的抽象就是有状态实…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
