【算法与数据结构】718、1143、1035、392、115、LeetCode最长重复子数组+最长公共子序列+不相交的线+判断子序列+不同的子序列
文章目录
- 一、718、最长重复子数组
- 二、1143、最长公共子序列
- 三、1035、不相交的线
- 四、392、判断子序列
- 五、115、不同的子序列
- 六、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、718、最长重复子数组
思路分析:
- 第一步,动态数组的含义。 d p [ i ] [ j ] dp[i][j] dp[i][j]代表以下标 i − 1 i - 1 i−1为结尾的nums1,和以下标 j − 1 j - 1 j−1为结尾的nums2,最长重复子数组长度为 d p [ i ] [ j ] dp[i][j] dp[i][j]。
- 第二步,递推公式。根据 d p [ i ] [ j ] dp[i][j] dp[i][j]的定义, d p [ i ] [ j ] dp[i][j] dp[i][j]的状态只能由 d p [ i − 1 ] [ j − 1 ] dp[i - 1][j - 1] dp[i−1][j−1]推导出来。
if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
- 第三步,元素初始化。dp数组中的所有元素都初始化为0。
- 第四步,递归顺序。一共有两层循环,先遍历nums1或者先遍历nums2都可以。
- 第五步,打印结果。题目要求长度最长的子数组的长度。所以在遍历的时候顺便把 d p [ i ] [ j ] dp[i][j] dp[i][j]的最大值记录下来。
程序如下:
// 718、最长重复子数组
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;if (dp[i][j] > result) result = dp[i][j];}}return result;}
};
复杂度分析:
- 时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m), n n n和 m m m分别是两个数组的长度。
- 空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)。
二、1143、最长公共子序列
思路分析:
- 第一步,动态数组的含义。 d p [ i ] [ j ] dp[i][j] dp[i][j]代表以下标 i − 1 i - 1 i−1为结尾的text1,和以下标 j − 1 j - 1 j−1为结尾的text2,最长公共子序列长度为 d p [ i ] [ j ] dp[i][j] dp[i][j]。
- 第二步,递推公式。 d p [ i ] [ j ] dp[i][j] dp[i][j]可以由两种情况推导出来:
- t e x t 1 [ i − 1 ] text1[i - 1] text1[i−1]与 t e x t 2 [ j − 1 ] text2[j - 1] text2[j−1]相同:那么找到一个公共元素, d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] + 1 dp[i][j] = dp[i - 1][j - 1] + 1 dp[i][j]=dp[i−1][j−1]+1。
- t e x t 1 [ i − 1 ] text1[i - 1] text1[i−1] 与 t e x t 2 [ j − 1 ] text2[j - 1] text2[j−1]不相同:那么 t e x t 1 [ 0 , i − 2 ] text1[0, i - 2] text1[0,i−2]与 t e x t 2 [ 0 , j − 1 ] text2[0, j - 1] text2[0,j−1]的最长公共子序列和 t e x t 1 [ 0 , i − 1 ] text1[0, i - 1] text1[0,i−1]与 t e x t 2 [ 0 , j − 2 ] text2[0, j - 2] text2[0,j−2]的最长公共子序列,取最大的。
if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
- 第三步,元素初始化。dp数组中的所有元素都初始化为0。
- 第四步,递归顺序。一共有两层循环,从前往后进行遍历。
- 第五步,打印结果。题目要求最长公共子序列的长度。所以在遍历的时候顺便把 d p [ i ] [ j ] dp[i][j] dp[i][j]的最大值记录下来。
程序如下:
// 1143、最长公共子序列
class Solution2 {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));int result = 0;for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);if(dp[i][j] > result) result = dp[i][j];}}return result;}
};
复杂度分析:
- 时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m), n n n和 m m m分别是两个序列的长度。
- 空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)。
三、1035、不相交的线


思路分析:本题要求绘制的最大连线数,实际上就是求两个字符串的最长公共子序列的长度,即1143、最长公共子序列这道题。我们将字符串改成数组,代码完全一样,直接copy过来。
程序如下:
// 1035、不相交的线
class Solution3 {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);if (dp[i][j] > result) result = dp[i][j];}}return result;}
};
复杂度分析:
- 时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m), n n n和 m m m分别是两个数组的长度。
- 空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)。
四、392、判断子序列
思路分析:本题的思路和1143、最长公共子序列的分析思路差不多,主要区别在于本题判断的是“ 最长公共子序列是不是另一个字符串的子串”。那么我们找到二者的最长公共子串,判断其长度是否等于s的长度即可。
- 第一步,动态数组的含义。 d p [ i ] [ j ] dp[i][j] dp[i][j]代表以下标 i − 1 i - 1 i−1为结尾的s,和以下标 j − 1 j - 1 j−1为结尾的t,最长公共子序列长度为 d p [ i ] [ j ] dp[i][j] dp[i][j]。
- 第二步,递推公式。 d p [ i ] [ j ] dp[i][j] dp[i][j]可以由两种情况推导出来:
- s [ i − 1 ] s[i - 1] s[i−1]与 t [ j − 1 ] t[j - 1] t[j−1]相同:那么找到一个公共元素, d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] + 1 dp[i][j] = dp[i - 1][j - 1] + 1 dp[i][j]=dp[i−1][j−1]+1。
- s [ i − 1 ] s[i - 1] s[i−1] 与 t [ j − 1 ] t[j - 1] t[j−1]不相同:那么 d p [ i ] [ j ] dp[i][j] dp[i][j]等于 s [ 0 , i − 1 ] s[0, i - 1] s[0,i−1]与 t [ 0 , j − 2 ] t[0, j - 2] t[0,j−2]的最长公共子序列。
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = dp[i][j - 1]; // 与1143不同的地方
- 第三步,元素初始化。dp数组中的所有元素都初始化为0。
- 第四步,递归顺序。一共有两层循环,从前往后进行遍历。
- 第五步,打印结果。题目要求最长公共子序列的长度。所以在遍历的时候顺便把 d p [ i ] [ j ] dp[i][j] dp[i][j]的最大值记录下来,在用三目运算符返回。
return result == s.size() ? true : false; // 与1143不同的地方
程序如下:
// 392、判断子序列-动态规划
class Solution4 {
public:bool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));int result = 0;for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = dp[i][j - 1]; // 与1143不同的地方if (dp[i][j] > result) result = dp[i][j];}}return result == s.size() ? true : false; // 与1143不同的地方}
};
复杂度分析:
- 时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m), n n n和 m m m分别是两个字符串的长度。
- 空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)。
五、115、不同的子序列

思路分析:本题的思路和1143、最长公共子序列的分析思路差不多。本题统计字符串t在字符串s中出现的次数,我们可以理解为删除掉字符串s中的部分字符使得字符串s和字符串t相同的方法数量。
-
第一步,动态数组的含义。 d p [ i ] [ j ] dp[i][j] dp[i][j]代表以下标 j − 1 j - 1 j−1为结尾的t在以下标 i − 1 i - 1 i−1为结尾的s中出现的次数为 d p [ i ] [ j ] dp[i][j] dp[i][j],即 t [ 0 , j − 1 ] t[0, j-1] t[0,j−1]在 s [ 0 , i − 1 ] s[0, i-1] s[0,i−1]中出现的次数。
-
第二步,递推公式。 d p [ i ] [ j ] dp[i][j] dp[i][j]可以由两种情况推导出来:
- s [ i − 1 ] s[i - 1] s[i−1]与 t [ j − 1 ] t[j - 1] t[j−1]相同:此时的 d p [ i ] [ j ] dp[i][j] dp[i][j]由两部分组成。一部分是用 s [ i − 1 ] s[i-1] s[i−1]来匹配:相当于在 s [ 0 , i − 2 ] s[0, i-2] s[0,i−2]中寻找 t [ 0 , j − 2 ] t[0, j-2] t[0,j−2]的个数(剩下一个字符 s [ i − 1 ] s[i - 1] s[i−1]与 t [ j − 1 ] t[j - 1] t[j−1]已经匹配了),即 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1];另一部分是不用 s [ i − 1 ] s[i-1] s[i−1]来匹配,相当于在 s [ 0 , i − 2 ] s[0, i-2] s[0,i−2]中寻找 t [ 0 , j − 1 ] t[0, j-1] t[0,j−1]的个数,即 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]。
- s [ i − 1 ] s[i - 1] s[i−1] 与 t [ j − 1 ] t[j - 1] t[j−1]不相同:那么 s [ 0 , i − 2 ] s[0, i - 2] s[0,i−2]中, t [ 0 , j − 1 ] t[0, j - 1] t[0,j−1]的数量和 s [ 0 , i − 1 ] s[0, i - 1] s[0,i−1]中, t [ 0 , j − 1 ] t[0, j - 1] t[0,j−1]的数量相同。 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j]
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; else dp[i][j] = dp[i - 1][j];
例子:s=“bageg”,t=“bag”。那么用s[4]="g"组成bag的方法数量,相当于在s[0, 3]="bage"中寻找中t[0, 1]="ba"的个数,只有s[0]s[1]s[4]这一种。而不用s[4]="g"组成bag的方法数量,相当于在s[0,3] ="bage"中,寻找t[0,2]="bag"的个数,即dp[4, 3],只有s[0]s[1]s[2]这一种。(说明:dp[4,2]=1代表在s[0,3] ="bage"中,t[0,1]="ba"的个数为1。)
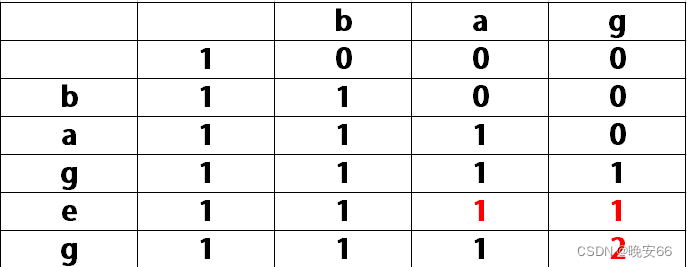
- 第三步,元素初始化。 d p [ i ] [ 0 ] dp[i][0] dp[i][0](第一列)表示字符串 s [ 0 , i − 1 ] s[0, i-1] s[0,i−1]中可以随便删除元素,出现空字符串的个数。 d p [ 0 ] [ j ] dp[0][j] dp[0][j](第一行)表示空字符串 s s s,出现字符串 t [ 0 , j − 1 ] t[0, j-1] t[0,j−1]的个数。其中,空字符串s中空字符串t的个数为1。那么 d p [ 0 ] [ 0 ] = 1 , d p [ i ] [ 0 ] = 1 , d p [ 0 ] [ j ] = 0 dp[0][0]=1, dp[i][0] = 1, dp[0][j] = 0 dp[0][0]=1,dp[i][0]=1,dp[0][j]=0。
- 第四步,递归顺序。一共有两层循环,从前往后进行遍历。
- 第五步,打印结果。
程序如下:
// 115、不同的子序列-动态规划
class Solution5 {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1, 0));for (int i = 0; i <= s.size(); i++) dp[i][0] = 1; // 第一列初始化为1, dp[0][0]为1for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 第一行初始化为0, 可以省略for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; else dp[i][j] = dp[i - 1][j];}}return dp[s.size()][t.size()];}
};
复杂度分析:
- 时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m), n n n和 m m m分别是两个字符串的长度。
- 空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)。
六、完整代码
# include <iostream>
# include <vector>
# include <string>
using namespace std;// 718、最长重复子数组
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;if (dp[i][j] > result) result = dp[i][j];}}return result;}
};// 1143、最长公共子序列
class Solution2 {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));int result = 0;for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);if (dp[i][j] > result) result = dp[i][j];}}return result;}
};// 1035、不相交的线-动态规划
class Solution3 {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);if (dp[i][j] > result) result = dp[i][j];}}return result;}
};// 392、判断子序列-动态规划
class Solution4 {
public:bool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));int result = 0;for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = dp[i][j - 1]; // 与1143不同的地方if (dp[i][j] > result) result = dp[i][j];}}return result == s.size() ? true : false; // 与1143不同的地方}
};// 115、不同的子序列-动态规划
class Solution5 {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1, 0));for (int i = 0; i <= s.size(); i++) dp[i][0] = 1; // 第一列初始化为1, dp[0][0]为1for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 第一行初始化为0, 可以省略for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; else dp[i][j] = dp[i - 1][j];}}return dp[s.size()][t.size()];}
};int main() {//vector<int> nums1 = { 1, 2, 3, 2, 1 }, nums2 = { 3, 2, 1, 4, 7 }; // 测试案例//Solution s1;//int result = s1.findLength(nums1, nums2);//string text1 = "abcde", text2 = "ace"; // 测试案例//Solution2 s1;//int result = s1.longestCommonSubsequence(text1, text2);//vector<int> nums1 = { 1, 4, 2 }, nums2 = { 1, 2, 4 }; // 测试案例//Solution3 s1;//int result = s1.maxUncrossedLines(nums1, nums2);//string s = "abc", t = "ahbgdc"; // 测试案例//Solution4 s1;//int result = s1.isSubsequence(s, t);string s = "babgbag", t = "bag"; // 测试案例Solution5 s1;int result = s1.numDistinct(s, t);cout << result << endl;system("pause");return 0;
}
end
相关文章:

【算法与数据结构】718、1143、1035、392、115、LeetCode最长重复子数组+最长公共子序列+不相交的线+判断子序列+不同的子序列
文章目录 一、718、最长重复子数组二、1143、最长公共子序列三、1035、不相交的线四、392、判断子序列五、115、不同的子序列六、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、718、最长重复子数组 思路分析࿱…...

OCR文本纠错思路
文字错误类别:多字 少字 形近字 当前方案 文本纠错思路 简单: 一、构建自定义词典,提高分词正确率。不在词典中,也不是停用词,分成单字的数据极有可能是错字(少部分可能是新词)。错字与前后的…...

【java批量导出pdf】优化方案
问题情境: 项目中存在web页面点击一键导出,导出所有数据对应的pdf文件,由于有些pdf文件是实时生成的,之前最简答的写法for循环处理速度太慢,超过了nginx配置的最大响应时间了,且对用户交互体验上很不友好&…...
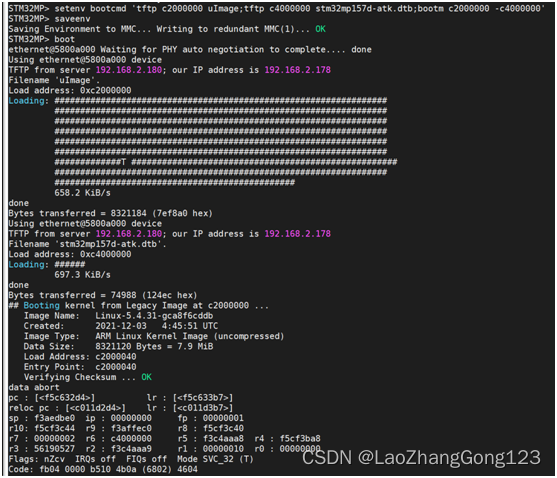
Linux第42步_移植ST公司uboot的第3步_uboot命令测试,搭建nfs服务器和tftp服务器
测试uboot命令,搭建nfs服务器和tftp服务器,是测试uboot非常关键的一步。跳过这一节,后面可能要踩坑。 一、输入“help回车”,查询uboot所支持的命令 二、输入“? bootz回车”,查询“bootz”怎么用 注意:和…...
)
C++枚举算法(3)
我家的门牌号 题目描述: 我家住在一条短胡同里,这条胡同的门牌号从1开始顺序编号。 若所有的门牌号之和减去我家门牌号的两倍,恰好等于n,求 我家的门牌号及总共有多少家。 数据保证有唯一解。 输入 一个正整数n。n < 100000。…...
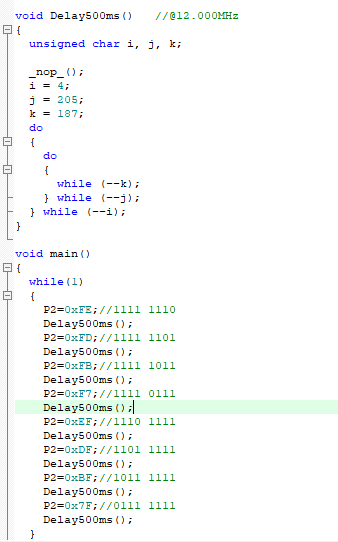
【51单片机】LED的三个基本项目(LED点亮&LED闪烁&LED流水灯)(3)
前言 大家好吖,欢迎来到 YY 滴单片机系列 ,热烈欢迎! 本章主要内容面向接触过单片机的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! YY的《C》专栏YY的《C11》专栏YY的…...

Day 17------C语言收尾之链表的删除、位运算、预处理、宏定义
链表 空链表: 注意:函数不能返回局部变量的地址 操作: 1.创建空链表 2.头插 3.尾插 4.链表遍历 5.链表的长度 free:释放 删除: 头删 void popFront(struct Node *head) { //1.p指针变量指向首节点 //2.断…...
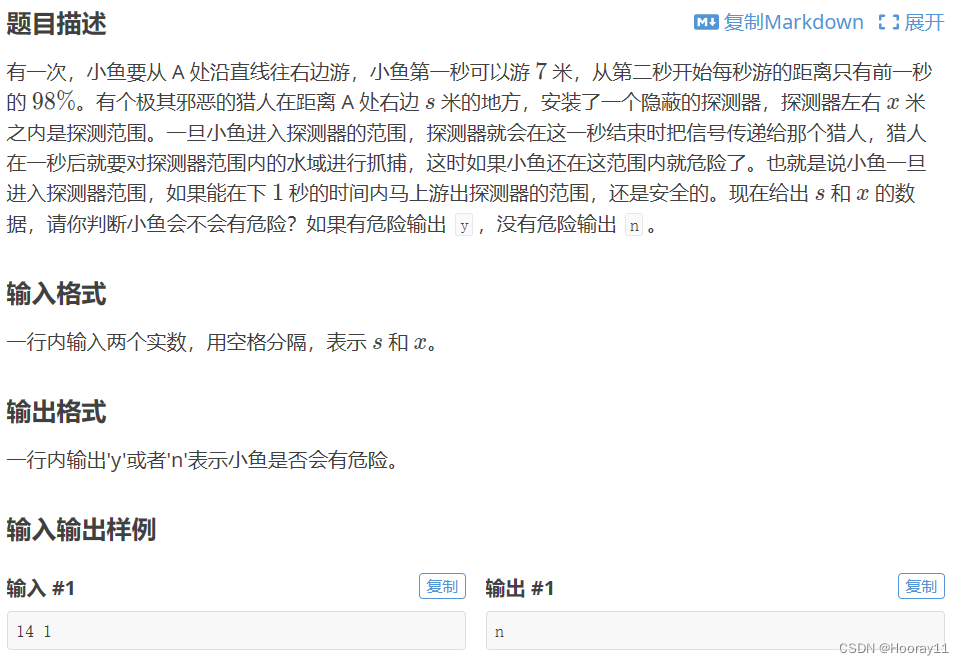
python_蓝桥杯刷题记录_笔记_全AC代码_入门5
前言 关于入门地刷题到现在就结束了。 题单目录 1.P1579 哥德巴赫猜想(升级版) 2.P1426 小鱼会有危险吗 1.P1579 哥德巴赫猜想(升级版) 一开始写的代码是三重循环,结果提交上去一堆地TLE,然后我就给减少…...

二叉树的详解
二叉树 【本节目标】 掌握树的基本概念掌握二叉树概念及特性掌握二叉树的基本操作完成二叉树相关的面试题练习 树型结构(了解) 概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。…...

【第三十五节】idea项目的创建以及setting和Project Structure的设置
项目创建 Project Structure的设置 点击file ~ Project Structure 进入...

【c++】跟webrtc学引用计数
rtc::RefCountInterface 接口类 G:\CDN\rtcCli\m98\src\rtc_base\ref_count.h引用计数想形成一种树状结构 // Interfaces where refcounting is part of the public api should // inherit this abstract interface. The implementation of these // methods is usually provid…...
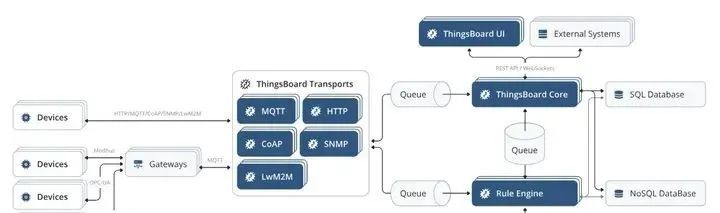
开源免费的物联网网关 IoT Gateway
1. 概述 物联网网关,也被称为IOT网关,是一种至关重要的网络设备。在物联网系统中,它承担着连接和控制各种设备的重要任务,将这些设备有效地连接到云端、本地服务器或其他设备上。它既能够在广域范围内实现互联,也能在…...

华为OD机试真题C卷-篇3
文章目录 查找一个有向网络的头节点和尾节点幼儿园篮球游戏 查找一个有向网络的头节点和尾节点 在一个有向图中,有向边用两个整数表示,第一个整数表示起始节点,第二个整数表示终止节点;图中只有一个头节点,一个或者多…...

[SWPUCTF 2021 新生赛]include
他让我们传入一个flag值 我们传入即可看到代码部分 传入一个php的伪类即可 得到经过Base64加密的flag,解密即可...
LeetCode、17. 电话号码的字母组合【中等,dfs回溯】
文章目录 前言LeetCode、17. 电话号码的字母组合【中等,dfs回溯】题目与类型思路递归回溯优化:StringBuilder来回溯补充代码:2024.1.31(简化) 资料获取 前言 博主介绍:✌目前全网粉丝2W,csdn博…...
SSRF漏洞给云服务元数据带来的安全威胁
文章目录 前言元数据服务威胁1.1 Metadata元数据1.2 RAM资源管理角色1.3 STS 临时凭据利用1.4 CF云环境利用框架1.5 元数据安全性增强 TerraformGoat2.1 永久性AccessKey2.2 SSRF靶场环境搭建2.3 腾讯云CVM配角色2.4 接管腾讯云控制台 SSRF组合拳案例3.1 上传图片功能SSRF3.2 文…...

【C++】强制类型转换
强制类型转换分为显式和隐式 显式直接用小括号强制转换,float b (int)a; 隐式直接 float b 0.5; int a b; C中更推荐用四个强制类型转换的关键字: 1、static_cast, 2、const_cast, 3、reinterpret_cast, 4、dynami…...
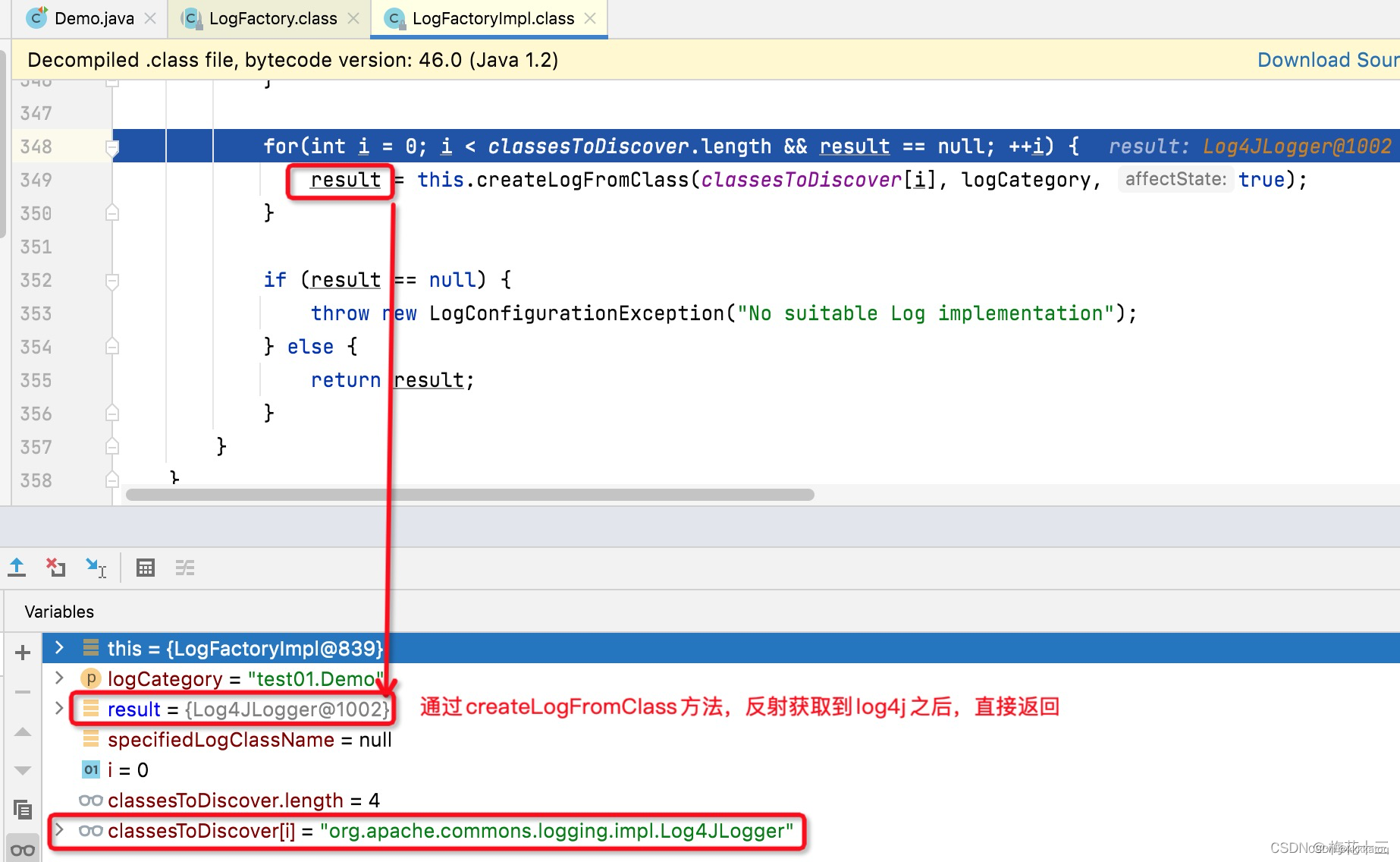
java日志框架总结(四 、JCL日志门面技术)
日志框架出现的历史顺序:Log4j → JUL → JCL → slf4j → logback → log4j2 一、背景 在前面博文中,我们分别讲述了常用的2个日志框架:JUL(Java Util Logging)、Log4J。那么如何选择使用哪一个呢? 根据项…...
mfc140.dll丢失的几种修复方式,有效的解决文件丢失问题
mfc140.dll是Microsoft Foundation Class (MFC)库中的一个非常重要的DLL文件。它承载了许多被执行程序使用的函数和资源。这个库主要被广泛应用于开发Windows操作系统上的应用程序。然而,有时候我们可能会遭遇到mfc140.dll缺失或损坏的情况,这会导致依赖…...
从一个小故事讲解观察者模式~
定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都得到通知并被自动更新。 什么是观察者模式? 观察者模式在我们的日常生活中极其常见。 先来看看观察者模式的定义: 观察者模式定义了对象之间…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
