SpringBoot 事务管理Transactional 数据回滚 数据一致性
介绍
SpringBoot当中的事物他保证了一致性,要么全部一起成功(提交),要么一起失败,失败(回滚)后数据会回到当初的样子,是一组操作的集合。
事物类型
- 开启事物
- 提交事物
- 回滚事物
案例
@Overridepublic void insert(Test t) {classesMapper.delete(1);//删除班级int n =1/0;//这里会发送异常testMapper.delete(1);//根据班级删除学生}
这是一个删除数据的方法,先删除班级,然后根据班级ID删除班级下的学生,但是走到第二行“ int n =1/0;”这里就会抛出异常,而且删除学生的方法并没有被执行,这样就导致了数据不一致。这种情况就可以使用事物来操作,发生了异常就回滚到之前的数据,保证了数据的完整性。要么一起成功,要么一起失败。
开启事物前置条件
表引擎必须为,InnoDB
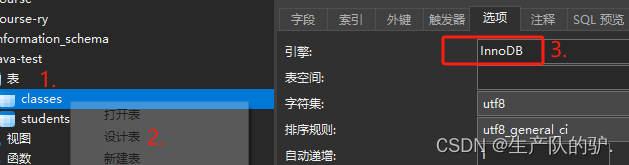
开启事物
@Transactional 在方法上添加 ,这样下来要么都删除成功,如果发送异常两个表的数据都不变化(回滚)。
开启事物 -> 发送错误-》提交事物-》回滚事物
@Override@Transactional //开启事物public void insert() {classesMapper.delete(1);//删除班级int n =1/0;//这里会发送异常testMapper.delete(1);//根据班级删除学生}
不同位置上添加
- 方法上添加:当前这个方法开启事物管理
- 类上:类中所有的方法开启事物管理
- 接口上:接口所有实现类的方法交给事务管理
相关文章:

SpringBoot 事务管理Transactional 数据回滚 数据一致性
介绍 SpringBoot当中的事物他保证了一致性,要么全部一起成功(提交),要么一起失败,失败(回滚)后数据会回到当初的样子,是一组操作的集合。 事物类型 开启事物提交事物回滚事物 案…...

vue使用pdf.js实现在线查看pdf文件
需求:有一个列表页,用户点击查看,弹层展示后台接口返回的pdf内容(不是文件、地址之类的,乱码的pdf铭文(二进制文件流)) 1、pdf.js安装 npm install --save vue-pdf2、正文代码 <template><div><el-table :data&q…...

java---查找算法(二分查找,插值查找,斐波那契[黄金分割查找] )-----详解 (ᕑᗢᓫ∗)˒
目录 一. 二分查找(递归): 代码详解: 运行结果: 二分查找优化: 优化代码: 运行结果(返回对应查找数字的下标集合): 编辑 二分查找(非递归…...
设置悬浮窗)
鸿蒙应用/元服务开发-窗口(Stage模型)设置悬浮窗
一、设置悬浮窗说明 悬浮窗可以在已有的任务基础上,创建一个始终在前台显示的窗口。即使创建悬浮窗的任务退至后台,悬浮窗仍然可以在前台显示。通常悬浮窗位于所有应用窗口之上;开发者可以创建悬浮窗,并对悬浮窗进行属性设置等操…...

springboot集成easypoi导出多sheet页
pom文件 <dependency><groupId>cn.afterturn</groupId><artifactId>easypoi-base</artifactId><version>4.1.0</version> </dependency> 导出模板: 后端代码示例: /*** 导出加油卡进便利店大额审批列…...
自己动手打包element UI官方手册文档教程
经常用element ui朋友开发的比较郁闷,官方文档网基本上都是打不开的, 官方:https://element.eleme.io/ 一直打不开,分析下是里面用的cdn链接ssl证书无效。 就想着自己搭建一个element UI文档 自己搭建的: Element文档网…...

《计算机网络简易速速上手小册》第5章:无线网络和移动通信(2024 最新版)
5.1 WLAN的工作原理 - 揭秘无线局域网络的魔法 5.1.1 基础知识 无线局域网络(WLAN)允许设备通过无线方式连接到一个局部区域网络,主要基于IEEE 802.11标准,俗称Wi-Fi。WLAN的核心是无线路由器,它不仅充当着网络中各设…...

2024PMP考试新考纲-近年PMP真题练一练和很详细解析(3)
今天华研荟继续为您分享和解析PMP真题,一方面让大家感受实际的PMP考试和出题形式,另一方面是通过较详细的解题思路和知识讲解帮助大家最后一个多月有效备考,一次性3A通过2024年PMP考试。 2024年PMP考试新考纲-近年真题随机练一练 (注&#x…...
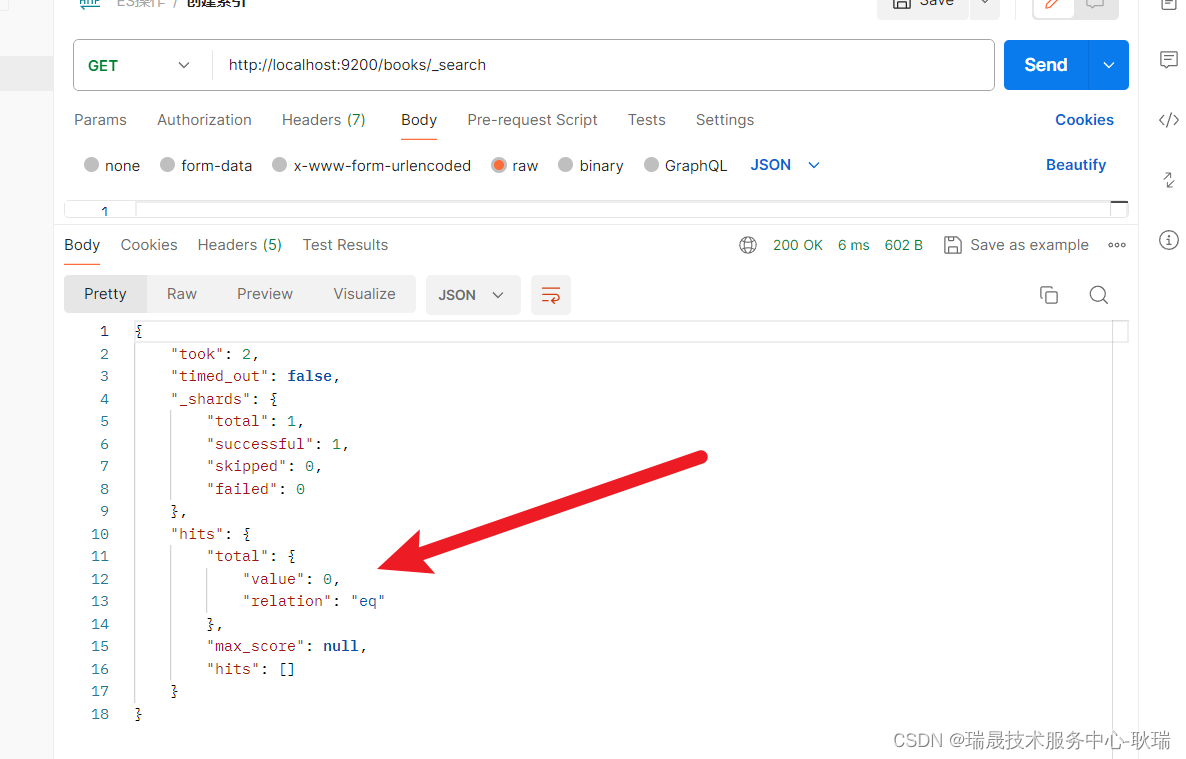
java SpringBoot2.7整合Elasticsearch(ES)7 进行文档增删查改
首先 我们在 ES中加一个 books 索引 且带有IK分词器的索引 首先 pom.xml导入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-elasticsearch</artifactId> </dependency>applicatio…...
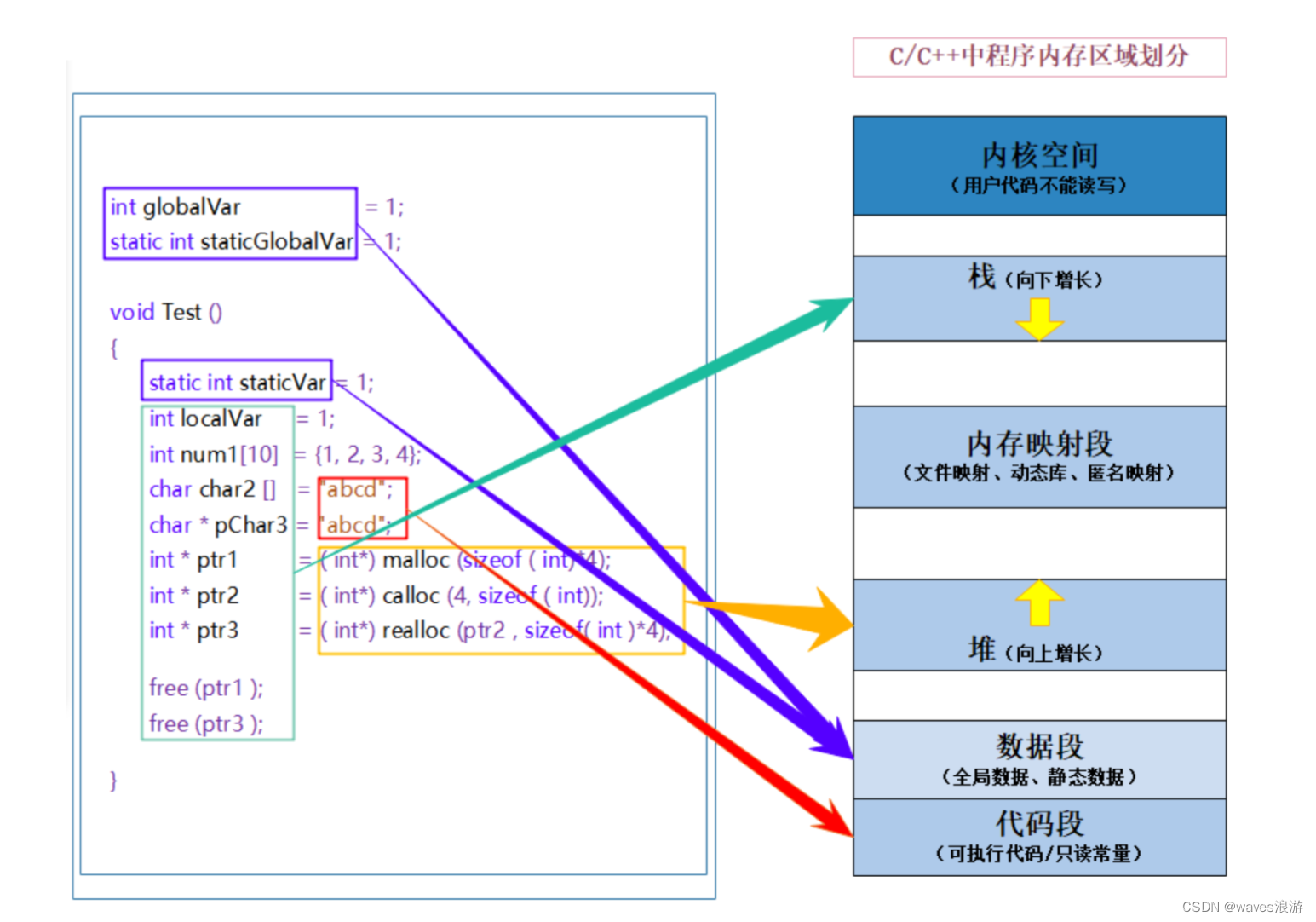
动态内存管理(2)
文章目录 4. 几个经典的笔试题4.1 题目14.2 题目24.3 题目34.4 题目4 5. C/C程序的内存开辟6. 动态通讯录7. 柔性数组7.1 柔性数组的特点7.2 柔性数组的使用7.3 柔性数组的优势 4. 几个经典的笔试题 4.1 题目1 #include <stdio.h> #include <stdlib.h> #include …...

使用 git 上传文件时,运行 命令 git pull origin 时未成功,出现报错信息
项目场景: 背景: 使用 git 上传文件时,运行 命令 git pull origin 时未成功,出现报错信息 问题描述 问题: $ git pull origin print --allow-unrelated-histories error: Pulling is not possible because you hav…...

Linux文件编译
目录 一、GCC编译 1.直接编译 2.分步编译 预处理: 编译: 汇编: 链接: 3.多文件编译 4.G 二、Make 1.概述 2.使用步骤 3.makefile创建规则 3.1一个基本规则 3.2两个常用函数 4.示例文件 三、GDB 示例:…...

homeword_day1
第一章 命名空间 一.选择题 1、编写C程序一般需经过的几个步骤依次是( B ) A. 编辑、调试、编译、连接 B. 编辑、编译、连接、运行 C. 编译、调试、编辑、连接 D. 编译、编辑、连接、运行 2、所谓数据封装就是将一组数据和与这组数据…...

ChatGPT论文指南|ChatGPT论文写作过程中6个润色与查重提示词
论文完成初稿之后,一般情况下,宝子们还需要找专家给我们提出评审意见。找专家评审其实并不容易,即使对老师来说,找人评审论文也是一件苦活。我们这个时候可以通过文字提示让 ChatGPT充当我们的评审专家,为论文提出问题…...

论文阅读:Learning Lens Blur Fields
这篇文章是对镜头模糊场进行表征学习的研究,镜头的模糊场也就是镜头的 PSF 分布,镜头的 PSF 与物距,焦距,光学系统本身的像差都有关系,实际的 PSF 分布是非常复杂而且数量也很多,这篇文章提出用一个神经网络…...
SpringBoot整合Knife4j接口文档生成工具
一个好的项目,接口文档是非常重要的,除了能帮助前端和后端开发人员更快地协作完成开发任务,接口文档还能用来生成资源权限,对权限访问控制的实现有很大的帮助。 这篇文章介绍一下企业中常用的接口文档工具Knife4j(基于…...
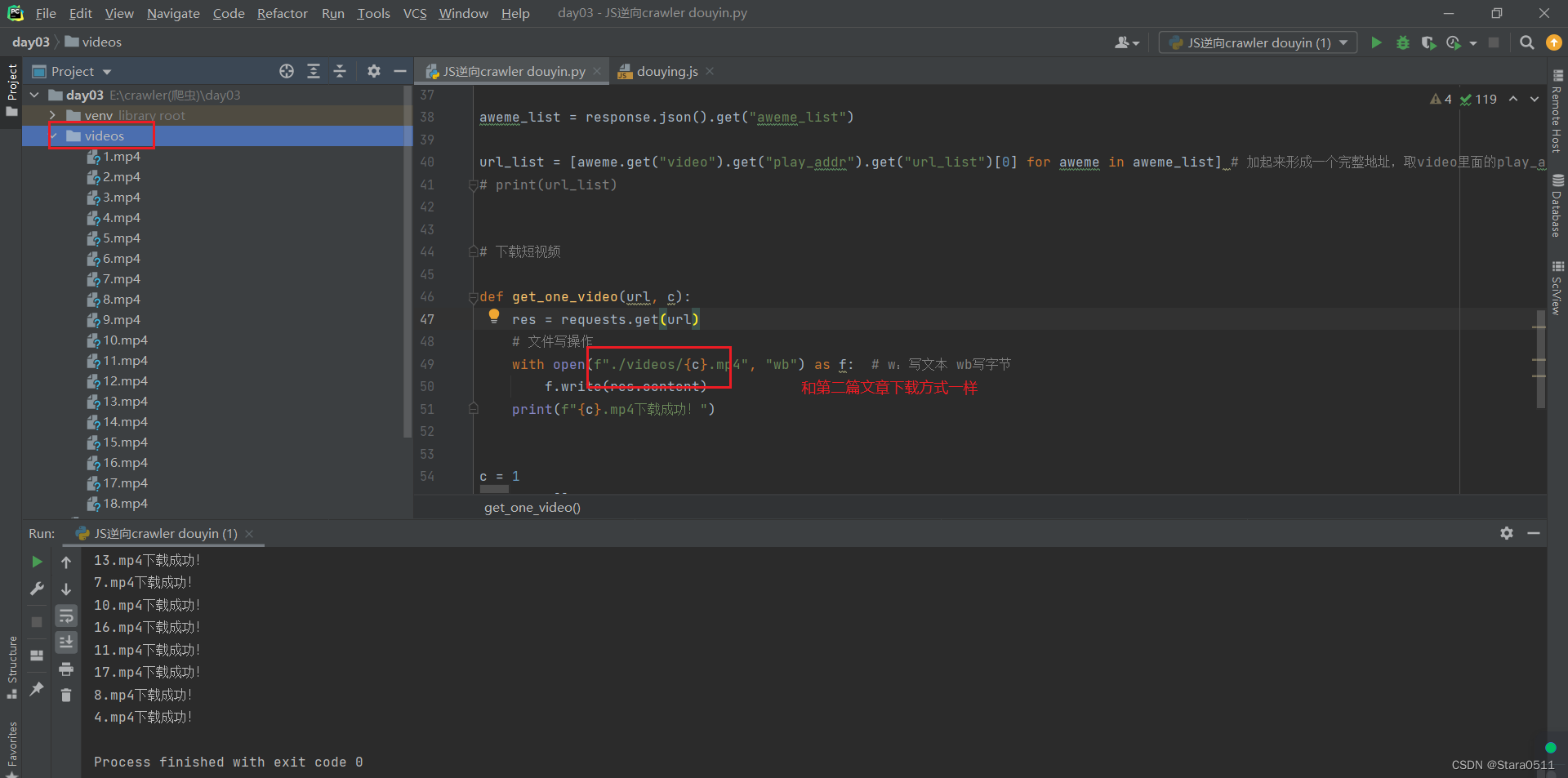
爬虫(三)
1.JS逆向实战破解X-Bogus值 X-Bogus:以DFS开头,总长28位 答案是X-Bogus,因为会把负载里面所有的值打包生成X-Boogus 1.1 找X-Bogus加密位置(请求堆栈) 1.1.1 绝招加高级断点(日志断点) 日志断点看有没有X-B值 日志…...
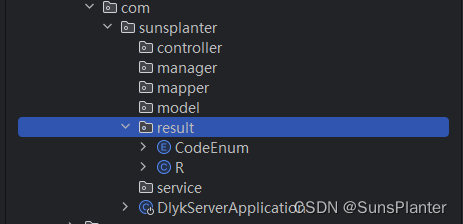
03 动力云客项目之登录功能后端实现
1 准备工作 1.1 创建项目 使用Spring initializr初始化项目 老师讲的是3.2.0, 但小版本之间问题应该不大. 1.2 项目结构 根据阿里巴巴Java开发手册确定项目结构 1.3 分层领域模型 【参考】分层领域模型规约: • DO(Data Object)&am…...

时光峰峦文物璀璨,预防性保护筑安全
在璀璨的历史长河中,珍贵文物如同时间的印记,承载着过往的辉煌。《人文山水时光峰峦——多彩贵州历史文化展》便是这样一场文化的盛宴,汇聚了众多首次露面的宝藏。然而,文物的保存对环境要求极为苛刻,温湿度波动都可能…...

Redis面试题43
人工智能在未来会有哪些可能的发展趋势? 答:人工智能在未来将继续迎来许多可能的发展趋势,以下是一些可能的方向: 更强大的算法和模型:人工智能算法和模型将不断改进和优化,为更复杂的数据和问题提供更强大…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
