NLP中的嵌入和距离度量
本文将深入研究嵌入、矢量数据库和各种距离度量的概念,并提供示例和演示代码。
NLP中的嵌入
嵌入是连续向量空间中对象、单词或实体的数值表示。在NLP中,词嵌入捕获词之间的语义关系,使算法能够更好地理解文本的上下文和含义。
让我们试着用一个例子和一些可视化的方法来理解它:假设有6个句子,想要创建嵌入
from sentence_transformers import SentenceTransformer# Sample text embedding modelmodel = SentenceTransformer('paraphrase-MiniLM-L6-v2')#Sentences we want to encode. Example:sentence = ['The team enjoyed the hike through the meadow','The team enjoyed the hike through the mountains','The team has not enjoyed the hike through the meadows','The national park had great views','There were lot of rare animals in national park','Olive oil drizzled over pizza tastes delicious']#Sentences are encoded by calling model.encode()embedding = model.encode(sentence)#Preview the embeddingsprint(embedding)# As we can see embeddings are nothing but # numerical representation of sentences in a vector form[[ 0.37061948 0.26414198 0.21265635 ... 0.14994518 -0.25794953-0.23970771][-0.07645706 0.27122658 -0.04530133 ... -0.27319074 -0.60025024-0.302555 ][ 0.35693657 -0.2331443 0.418002 ... -0.37369558 -0.10241977-0.03282997][ 0.66933334 0.40094966 -0.48208416 ... 0.10645878 -1.5067163-0.01547382][ 0.4339616 0.2323563 0.21751338 ... -0.5746389 -0.264384540.492655 ][-0.2655593 0.11172348 -0.1473308 ... 0.42197517 0.883945760.10763898]]
可以看到我们获得了一个384维度的嵌入
embedding.shape(6, 384)
然后我们使用PCA进行降维并使用matplot可视化
from sklearn.decomposition import PCA# Perform PCA for 2D visualizationPCA_model = PCA(n_components = 2)PCA_model.fit(embedding)new_embeddings = PCA_model.transform(embedding)# As we can see now the shape has changed from (6,384)->(6,2)Shape: (6, 2)[[-2.7454064 -1.628386 ][-2.7024133 -2.0113547 ][-2.6084075 -2.5289955 ][ 0.62488586 3.9073005 ][ 0.09110744 4.9031897 ][ 7.3402357 -2.6417546 ]]
PCA将其维度降维2 这样可以显示在2D的散点图上
import matplotlib.pyplot as pltimport mplcursorsdef plot2d(x_values, y_values, text_labels):"""Create a 2D plot with annotations.Parameters:- x_values (array): X-axis values.- y_values (array): Y-axis values.- text_labels (list): List of text labels for each point."""fig, ax = plt.subplots()scatter = ax.scatter(x_values, y_values, label='Data Points')# Annotate points with text labelsfor i, label in enumerate(text_labels):ax.annotate(label, (x_values[i], y_values[i]))mplcursors.cursor(hover=True)ax.set_xlabel('X-axis')ax.set_ylabel('Y-axis')ax.set_title('2D Plot with Annotations')plt.show()
调用这个函数,结果如下
import matplotlib.pyplot as pltimport mplcursors# pass the embeddings and original sentence to create labelsplot2d(new_embeddings[:,0], new_embeddings[:,1], sentence)

现在你可以看到,彼此相似的句子被投影到彼此附近,这实际很有意义。例如,提到“National Park”的句子彼此靠得更近,谈论“hiking”的句子彼此靠得更近。
如何度量这些句子嵌入之间的距离?
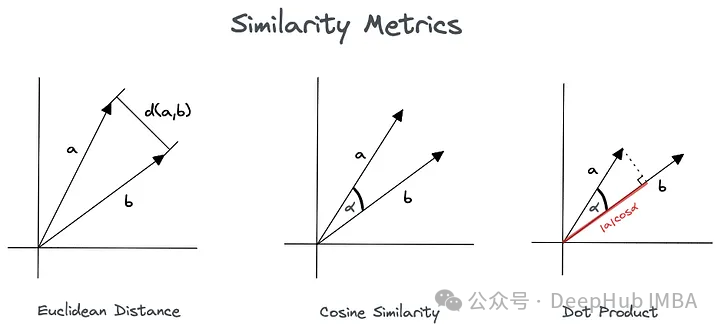
有很多方法可以计算两个向量之间的距离,我们将介绍矢量数据库中常用的4种距离度量
1、欧氏距离
两个向量之间最短路径的长度

欧几里得距离很容易理解,因为它测量空间中两点之间的直线距离。它适用于矢量元素之间的大小和绝对差异很重要的情况。
但是欧氏距离对数据的尺度很敏感。如果特征具有不同的尺度,则距离计算可能被尺度较大的特征所主导。并且在高维空间中,欧几里得距离可能变得不那么有意义,因为由于“维度诅咒”,距离趋于收敛。
考虑二维空间中的两点:A(1,2)和B (4,6), A和B之间的欧氏距离计算为:

2、余弦距离
测量矢量之间的方向性差异

余弦距离不受向量大小的影响,使其对尺度差异具有鲁棒性,非常适合高维空间。
余弦距离只考虑向量的方向,而不是它们的大小。如果两个矢量方向相似,但长度相差很大,那么它们的余弦相似度可能接近于0。

3、Jaccard

Jaccard系数度量有限样本集之间的相似性,定义为交集的大小除以样本集并集的大小:

在处理集合或二元数据时,Jaccard特别有用,使其适用于文本文档比较等场景。像余弦相似度一样,Jaccard对大小不敏感。
但是它主要是为二元数据设计的,它可能不适合连续数据或大小信息至关重要的情况。当两个集合都为空时,Jaccard相似度是未定义的。
4、曼哈顿距离

曼哈顿距离,也称为L1距离或出租车距离,它测量基于网格的系统中两点之间的距离,只考虑水平和垂直运动。
曼哈顿距离直观且易于解释。它对应于出租车在网格状道路系统上行驶的距离,在水平和垂直方向上行驶以到达目的地。这种简单性使得它在可解释性至关重要的场景中特别有用。
曼哈顿距离在处理以表格形式表示的基于网格的系统或数据集时非常适用。它非常适合沿网格线移动的场景,例如在物流、运输和图像处理中。
但是曼哈顿距离的一个重大缺点是它对数据规模的敏感性。如果特征具有不同的尺度,则距离计算可能被尺度较大的特征所主导。在处理特征大小不同的数据集时,这可能导致次优结果。
并且曼哈顿距离本质上受限于沿水平和垂直轴的网格运动。在特征之间的对角线移动或非线性关系至关重要的情况下,曼哈顿距离可能无法准确捕获数据中的潜在模式。
余弦相似度vs正弦相似度
还有一个更有趣的问题是为什么我们用余弦而不是正弦相似度来测量矢量距离。

余弦相似度比正弦相似度更常用于测量向量之间的相似度。余弦和正弦相似度之间的选择取决于数据的性质和任务的具体要求。让我们来探讨一下为什么余弦相似度是首选:
余弦相似度度量的是矢量之间的夹角余弦值,而正弦相似度度量的是夹角的正弦值。余弦相似度更直接地表示矢量指向的相似度,而正弦相似度则在一些情况下可能不如余弦相似度直观。
余弦相似度的计算中包含了矢量的内积,而正弦相似度则涉及到矢量的外积。在高维空间中,矢量之间的内积更容易计算,而外积可能涉及到复杂的计算。因此余弦相似度的计算在实际应用中更为高效。
余弦相似度与向量之间的角度直接相关。余弦相似度为1表示向量指向相同的方向,而相似度为-1表示它们指向相反的方向。相似度为0表示正交性。这种直观的解释与许多应用程序非常吻合。
正弦相似度在实践中不太常见是它测量向量间夹角的正弦值,强调相似度的垂直分量。虽然正弦相似度可能有特定的用例,例如垂直度至关重要的场景,但余弦相似度由于其在规范化、定向解释和效率方面的优势而被更广泛地采用。
总结
本文探讨了嵌入和距离度量的概念,理解和利用这些概念对于在各个领域构建高级NLP模型和应用程序至关重要。因为在实际应用中需要考虑尝试不同的模型、数据库和指标,并针对特定用例进行优化性能。
https://avoid.overfit.cn/post/8c9ee01acff64699bdc8a194c0e1247b
相关文章:

NLP中的嵌入和距离度量
本文将深入研究嵌入、矢量数据库和各种距离度量的概念,并提供示例和演示代码。 NLP中的嵌入 嵌入是连续向量空间中对象、单词或实体的数值表示。在NLP中,词嵌入捕获词之间的语义关系,使算法能够更好地理解文本的上下文和含义。 让我们试着用…...
jsp教务管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 JSP 教务管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&…...

基恩士 KV-8000 PLC通讯简单测试
1、KV-8000通讯协议 基恩士 KV-8000 PLC支持多种通讯方式,包括:OPC UA、Modbus、上位链路命令等。其中OPC UA需要对服务器和全局变量进行设置,Modbus需要调用功能块。默认支持的是上位链路命令,实际是一条条以回车换行结束的ASCII…...

【高质量精品】2024美赛B题22页word版高质量半成品论文+多版保奖思路+数据+前四问思路代码等(后续会更新)
一定要点击文末的卡片,进入后,获取完整论文!! B 题整体模型构建 1. 潜水器动力系统失效:模型需要考虑潜水器在无推进力情况下的行为。 2. 失去与主船通信:考虑无法从主船接收指令或发送位置信息的情况。…...

apache_exporter安装说明
Apache Exporter 问题描述 需要监控apache服务,部署了apache_exporter,对过程进行一下记录。 源码参见apache_exporter ①下载 https://github.com/Lusitaniae/apache_exporter/releases②解压缩 tar -xzvf apache_exporter-0.7.0.linux-amd64.tar…...

代码随想录算法训练营29期Day42|卡码网46,LeetCode 416
文档讲解:背包问题二维 背包问题一维 分割等和子集 46.整数拆分 题目链接:https://kamacoder.com/problempage.php?pid1046 思路: 在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为d…...
java的excel列行合并模版
1.效果 2.模版 <tableborder"1"cellpadding"0"cellspacing"0"class"tablebor"id"TABLE"><tr align"center" class"bg217"><td style"background-color: #008000; color: #ffffff;p…...
【ES数据可视化】kibana实现数据大屏
目录 1.概述 2.绘制数据大屏 2.1.准备数据 2.2.绘制大屏 3.嵌入项目中 1.概述 再来重新认识一下kibana: Kibana 是一个用于数据可视化和分析的开源工具,是 Elastic Stack(以前称为 ELK Stack)中的一部分,由 Ela…...

2024 年十大 Vue.js UI 库
Vue.js 是一个流行的 JavaScript 框架,它在前端开发者中越来越受欢迎,以其简单、灵活和易用性而闻名。 Vue.js 如此受欢迎的原因之一是它拥有庞大的 UI 库生态系统。 这些库为开发人员提供了预构建的组件和工具,帮助他们快速高效地构建漂亮…...
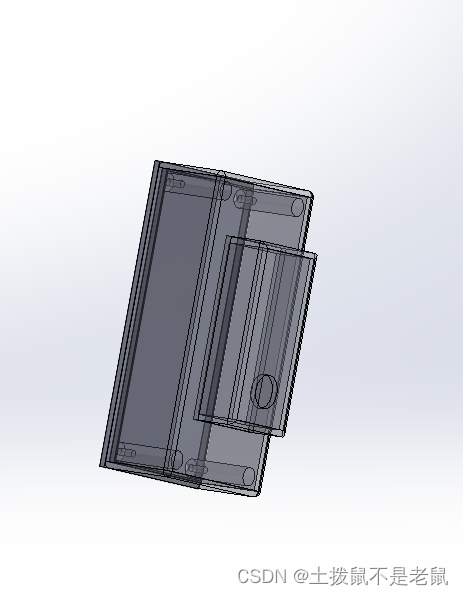
使用esp32 cam + SR602人体感应模块制作一个小型的监控
需求: 做一个小型的监控,类似电子猫眼,监测到人之后,取一张图 然后发送到自己的邮箱。 架构: 1.sr602 传感器监测到人 2. esp32 cam 取图 并通过mqtt协议传到远端服务器 3, 服务器利用python 搭建一个mqtt客户端&…...

vim最简单命令学习
安装vim sudo apt install vim在终端随便打开一个文本文件,或者源文件, vim filepath输入该命令后,从终端进入vim编辑器,此时为普通模式(Normal)。 按i键进入编辑模式(Insert),按Esc键返回普通模式(Normal)。 在编辑…...

论文阅读-通过云特征增强的深度学习预测云工作负载转折点
论文名称:Cloud Workload Turning Points Prediction via Cloud Feature-Enhanced Deep Learning 摘要 云工作负载转折点要么是代表工作负载压力的局部峰值点,要么是代表资源浪费的局部谷值点。预测这些关键点对于向系统管理者发出警告、采取预防措施以…...

Android Studio从零基础到APP上线(3)
第3章 简单控件 本章介绍App开发常见的几类简单控件的用法,主要包括:显示文字的文本视图,容纳视图的常用布局,响应点击的按钮控件,显示图片的图像视图等。然后结合本章所学的知识,演示一个实战项目“简单计算器”的设计与实现。 3.1 文本显示 本节介绍如何在文本视图Tex…...

springboot Feign方式注入注解详解
一、FeignClient注解详解 FeignClient是Spring Cloud中用于声明Feign客户端的注解,它使得编写HTTP客户端变得更简单。通过Feign的自动化配置机制,可以很容易地编写HTTP API客户端。以下是FeignClient的详解: 作用:FeignClient注解…...
自然语言处理(NLP)—— Dialogflow ES聊天机器人
1. 背景介绍 这个实验室的目标是让你了解并使用Google的Dialogflow服务。Dialogflow是一个可以让你创建聊天机器人的服务,这个过程不需要或者只需要很少的编程技能。 1.1 账号的创建 为了完成这个实验室,你需要在以下网站上创建账号:…...

C++俄罗斯方块 -- 菜单展示和选择 -- 方法
short Menu() //选中开始游戏返回1,离开则返回2 {short choice 1;//跟踪用户选中的选项char c; //记录用户按键信息system("cls");SetPos(9, 12); //设置输出坐标,12行9列cout << "┌────────┐";SetPos(9, 13);cou…...
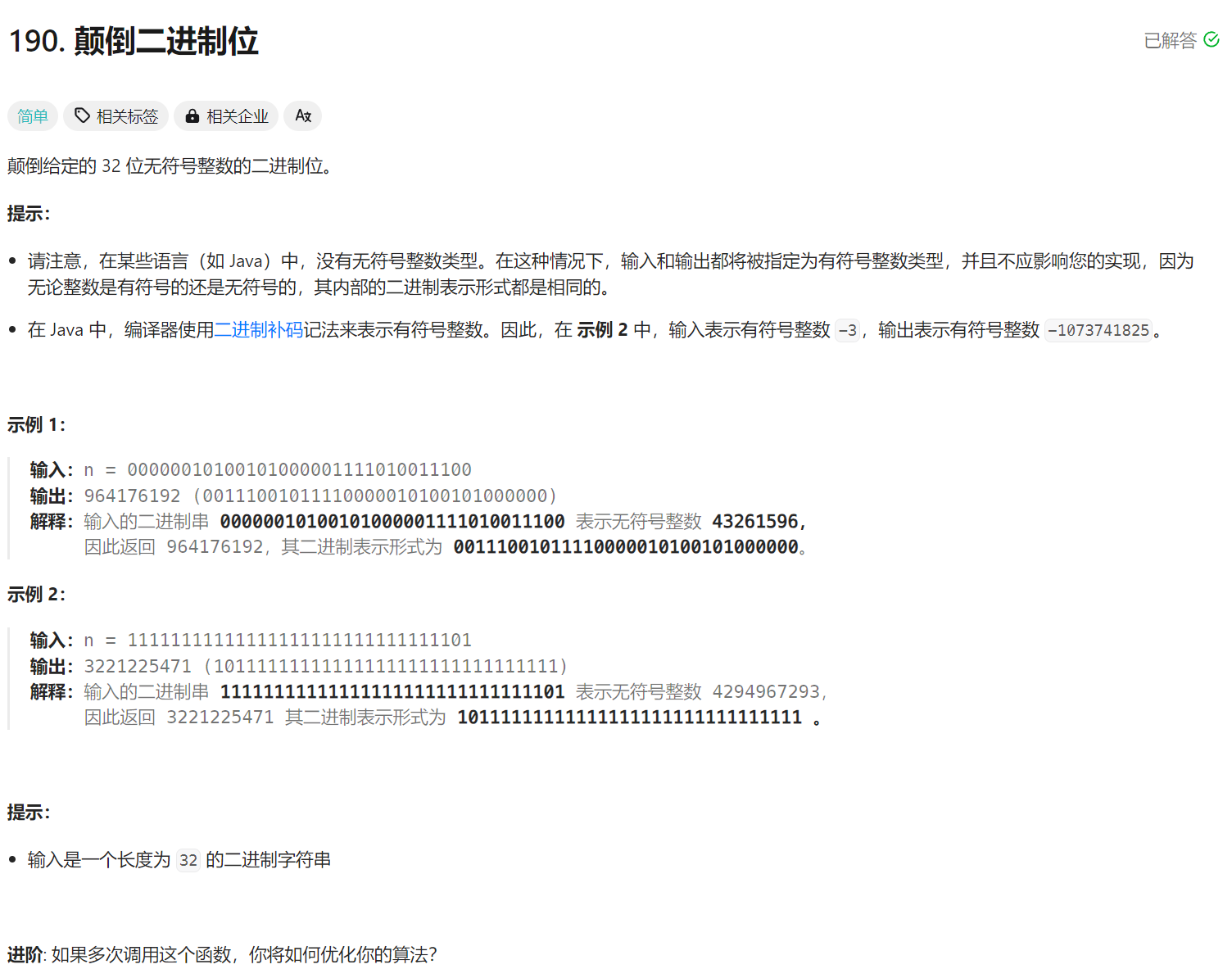
面试150 颠倒二进制位 位运算分治 逻辑右移
Problem: 190. 颠倒二进制位 文章目录 思路复杂度位运算分治法 思路 👨🏫 参考题解 >>>:逻辑右移(符号位一起移动,高位补零) 复杂度 时间复杂度: O ( log n ) O(\log{n}) O(logn) 空间…...

php 函数三
一 对称加密 1.1 openssl 1.1.1 openssl_get_cipher_methods(bool $aliases false) 获取可用的加密算法。包含可用加密算法的array。 请注意:在 OpenSSL 1.1.1 版本之前,返回加密算法的拼法大小写都有; 从 OpenSSL 1.1.1 开始,…...

Windows下配置多个账号的git ssh
生成密钥 已经有一个密钥的情况下,用下面的命令生成一个新密钥,注意为了防止原始密钥文件被覆盖,需要给一个新名字: ssh-keygen -t rsa -f C:\\Users\\xxx\\.ssh\\id_rsa_xxx -C "xxxemail.com"给GitHub配置SSH Key …...
【漏洞复现】电信网关配置管理系统SQL注入漏洞
Nx01 产品简介 电信网关配置管理系统是一个用于管理和配置电信网络中网关设备的软件系统。它可以帮助网络管理员实现对网关设备的远程监控、配置、升级和故障排除等功能,从而确保网络的正常运行和高效性能。 Nx02 漏洞描述 电信网关配置管理系统存在SQL注入漏洞,攻…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
