机器学习 | 揭示EM算法和马尔可夫链的实际应用
目录
初识EM算法
马尔可夫链
HMM模型基础
HMM模型使用
初识EM算法
EM算法是一种求解含有隐变量的概率模型参数的迭代算法。该算法通过交替进行两个步骤:E步骤和M步骤,从而不断逼近模型的最优参数值。EM算法也称期望最大化算法,它是一个基础算法,是很多机器学习领域算法的基础,比如隐式马尔可夫算法(HMM)等等。
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步:
其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法。
EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题,其算法基础和收敛有效性等问题,其基本思想是:
1)首先根据已经给出的观测数据,估计出模型参数的值
2)然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计
3)然后反复迭代,直至最后收敛,迭代结束。
EM算法计算流程如下:

极大似然估计: 极大似然估计是一种常用的统计方法,用于从观测数据中估计概率模型的参数。它的基本思想是寻找在给定观测数据条件下使得概率模型产生观测数据的概率最大的参数值。
假如我们需要调查学校的男生和女生的身高分布,我们抽取100个男生和100个女生,将他们按照性别划分为两组。然后,统计抽样得到100个男生的身高数据和100个女生的身高数据。

我们知道样本所服从的概率分布模型和一些样本,我们需要求解该模型的参数,
我们已知的条件有两个:
1)样本服从的分布模型 2)随机抽取的样本。
我们需要求解模型的参数,根据已知条件,通过极大似然估计,求出未知参数。
以下是最大似然函数估计值的求解步骤:

马尔可夫链
马尔可夫链(Markov Chain)是一种随机过程,通常用于建模具有“无记忆性”特征的序列数据。在马尔可夫链中,当前状态只取决于前一个状态,而与更早的状态无关。在机器学习算法中,马尔可夫链是个很重要的概念。又称离散时间马尔可夫链,因俄国群学家安德烈·马尔可夫得名。
马尔可夫链即为状态空间中从一个状态到另一个状态转换的随机过程:

该过程要求具备“无记忆"的性质:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性"称作马尔可夫性质。
马尔可夫链作为实际过程的统计模型具有许多应用,在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。态的改变叫做转多,与不同的状态改变相关的概率叫做转移概率。
马尔可夫链的数学表示如下:

某一时刻状态转移的概率只依赖前一个状态,那么只要求出系统中任意两个状态之间的转移概率,这个马尔可夫链的模型就定了。以下是马尔可夫链的经典案例:
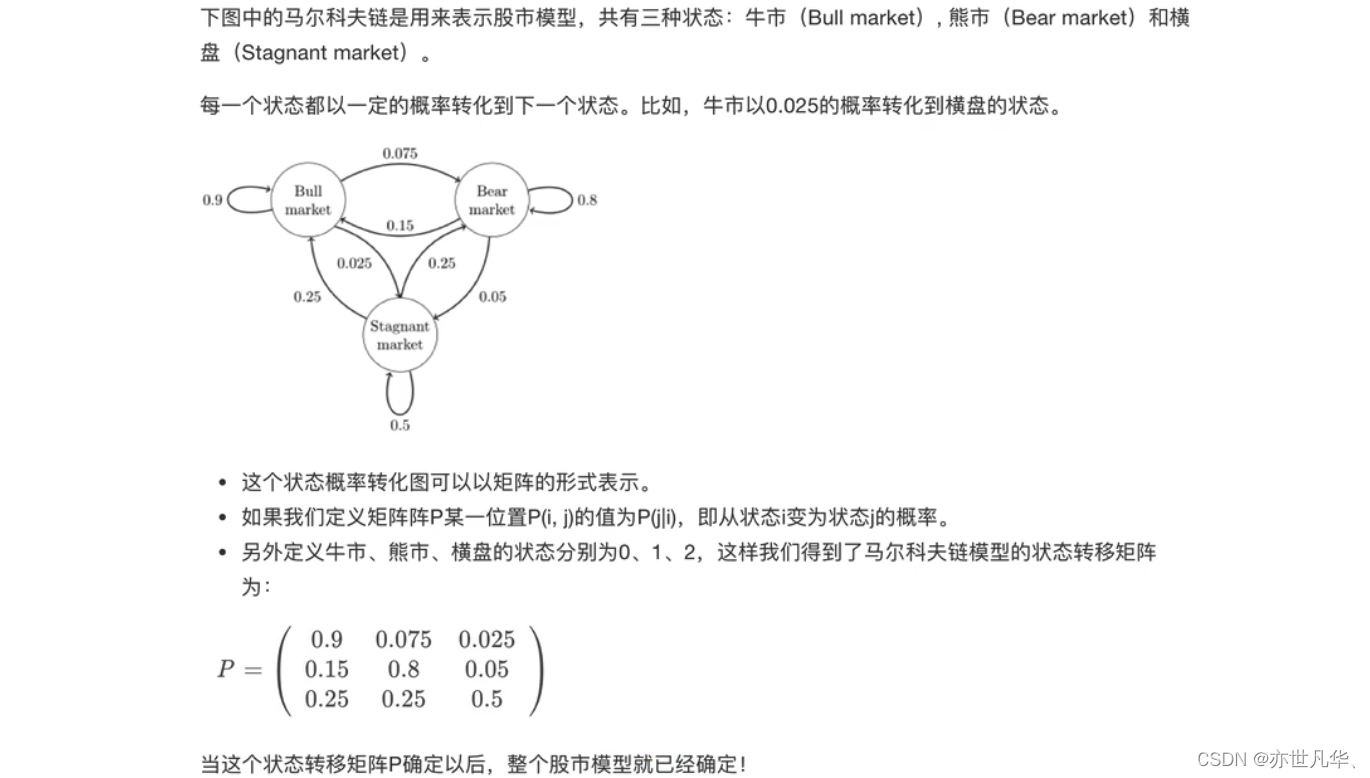
HMM模型:隐马尔可夫模型是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。通过以下简单案例来介绍:



其实对于HMM来说,如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。但是应用HMM模型时候呢,往往是缺失了一部分信息的。和HMM模型相关的算法主要分为三类,分别解决三种问题:
1)知道般子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种般子(隐含状态链)。



2)还是知道骰子有几种(隐含状态数量),每种般子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。


3)知道骰子有几种(隐含状态数量),不知道每种般子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种般子是什么(转换概率)。




HMM模型基础
HMM模型是基于马尔可夫链的一种概率图模型,广泛应用于语音识别、自然语言处理、生物信息学等领域。与普通的马尔可夫链不同,HMM模型包含两个状态集合:观测状态集合和隐藏状态集合。观测状态表示我们可以直接观察到的状态,隐藏状态则表示我们无法直接观察到的状态。隐藏状态之间仍然满足马尔可夫性质,即当前状态只与前一个状态有关。
HMM模型做了两个很重要的假设如下:
齐次马尔科夫链假设:

观测独立性假设:

什么样的问题需要HMM模型?

HMM模型实例:下面我们用一个简单的实例来描述上面抽象出的HMM模型。这是一个盒子与球的模型:
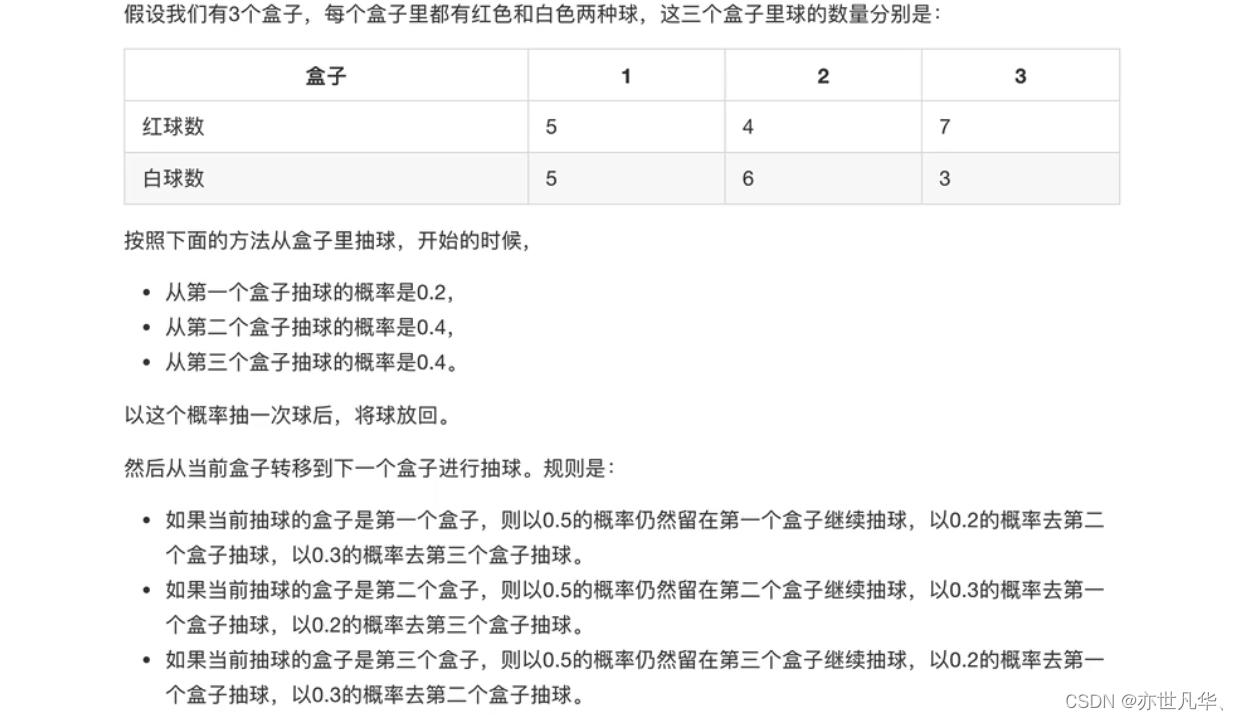

HMM观测序列的生成:

HMM模型的三个基本问题:

HMM模型使用
有多个库可以用来实现HMM模型,这里我就拿常用的hmmlearn库进行举例,hmmlearn是一个基于scikit-learn的Python库,提供了多种HMM模型及其变体的实现。它支持高斯混合模型和多项式分布模型,可以用于多个领域的序列学习问题。以下是其安装命令,终端执行如下命令安装:
pip install hmmlearn -i https://pypi.mirrors.ustc.edu.cn/simplehmmlearn实现了三种HMM模型类,按照观测状态是连续状态还是离散状态,可以分为两类。
GaussianHMM和GMMHMM是连续观测状态的HMM模型,而MultinomiaIHMM是离散观测状态的模型,也是我们在HMM原理系列篇里面使用的模型。在这里主要介绍我们前面一直讲的关于离散状态的MultinomialHMM模型。对于MultinomialHMM的模型,使用比较简单:
1)tartprob_"参数对应我们的隐藏状态初始分布Ⅱ。
2)transmat_"对应我们的状态转移矩阵A。
3)emissionprob_"对应我们的观测状态概率矩阵B。
以下是使用HMM模型的基础案例讲解:
# 导入相应模块
import numpy as np
from hmmlearn import hmm下面这段代码是一个使用隐马尔可夫模型进行建模的示例,这些参数的设定是HMM模型的基础,它们描述了隐藏状态和观测状态之间的关系。在实际应用中,你可以根据具体问题来设定这些参数,然后使用HMM模型进行概率计算、状态预测等任务:
# 设定隐藏状态的集合
states = ["box 1", "box 2", "box 3"]
n_states = len(states)# 设定观察状态的集合
observations = ["red", "white"]
n_observations = len(observations)# 设定初始状态分布
start_probability = np.array([0.2, 0.4, 0.4])# 设定状态转移概率分布矩阵
transition_probability = np.array([[0.5, 0.2, 0.3],[0.3, 0.5, 0.2],[0.2, 0.3, 0.5]])# 设定观测状态概率矩阵
emission_probability = np.array([[0.5, 0.5],[0.4, 0.6],[0.7, 0.3]])下面这段代码是使用hmmlearn库中的CategoricalHMM模型来进行隐马尔可夫模型建模的示例,利用这个已经初始化好的模型对象进行概率计算、状态预测等任务。这里的CategoricalHMM模型是用于处理离散观测状态的情况,如果观测状态是连续值,可以考虑使用GaussianHMM模型:
# 定义模型
model = hmm.CategoricalHMM(n_components=n_states)# 设定模型参数
model.startprob_ = start_probability # 初始化状态分布
model.transmat_ = transition_probability # 初始化状态转移概率分布矩阵
model.emissionprob_ = emission_probability # 初始化观测状态概率矩阵对于 HMM 问题三:维特比算法的解码过程,使用和之前一样的观测序列来解码:

# 维特比模型训练
box = model.predict(seen)print("球的观测顺序为:", ' → '.join(map(lambda x: observations[x], seen.flatten())))
# 注意:需要使用flatten方法,把seen从二维变成一维
print("最可能的隐藏状态序列为:", ' → '.join(map(lambda x: states[x], box)))得到的结果如下所示:

如果求 HMM 问题一的观测序列的概率的问题,代码如下:
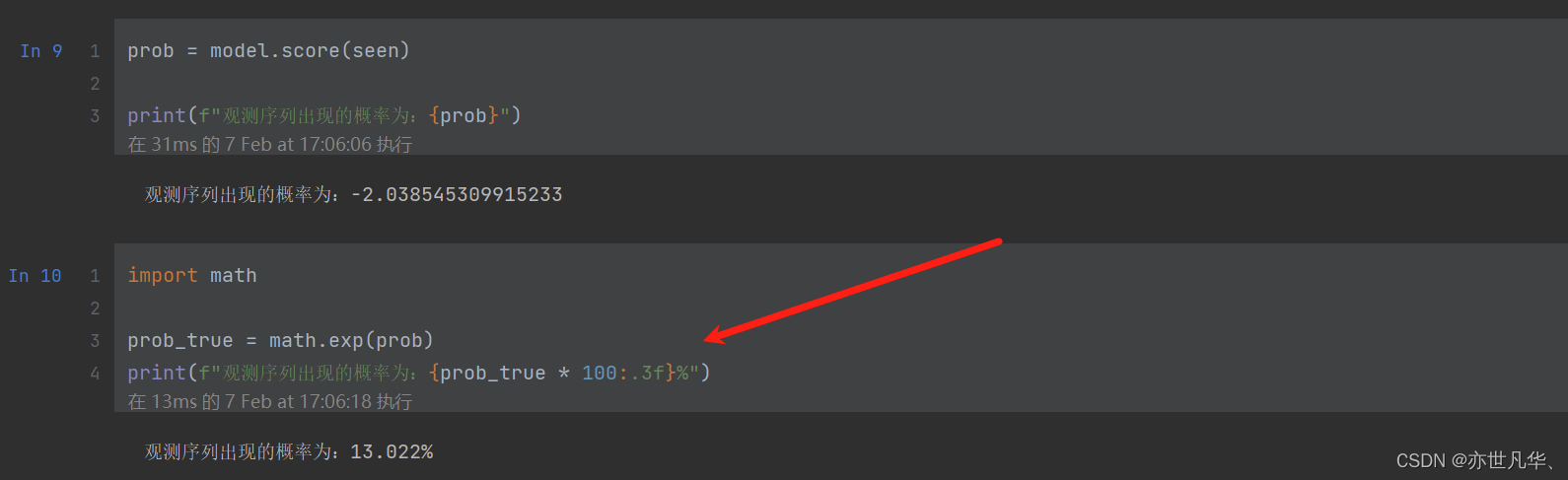
相关文章:

机器学习 | 揭示EM算法和马尔可夫链的实际应用
目录 初识EM算法 马尔可夫链 HMM模型基础 HMM模型使用 初识EM算法 EM算法是一种求解含有隐变量的概率模型参数的迭代算法。该算法通过交替进行两个步骤:E步骤和M步骤,从而不断逼近模型的最优参数值。EM算法也称期望最大化算法,它是一个基…...
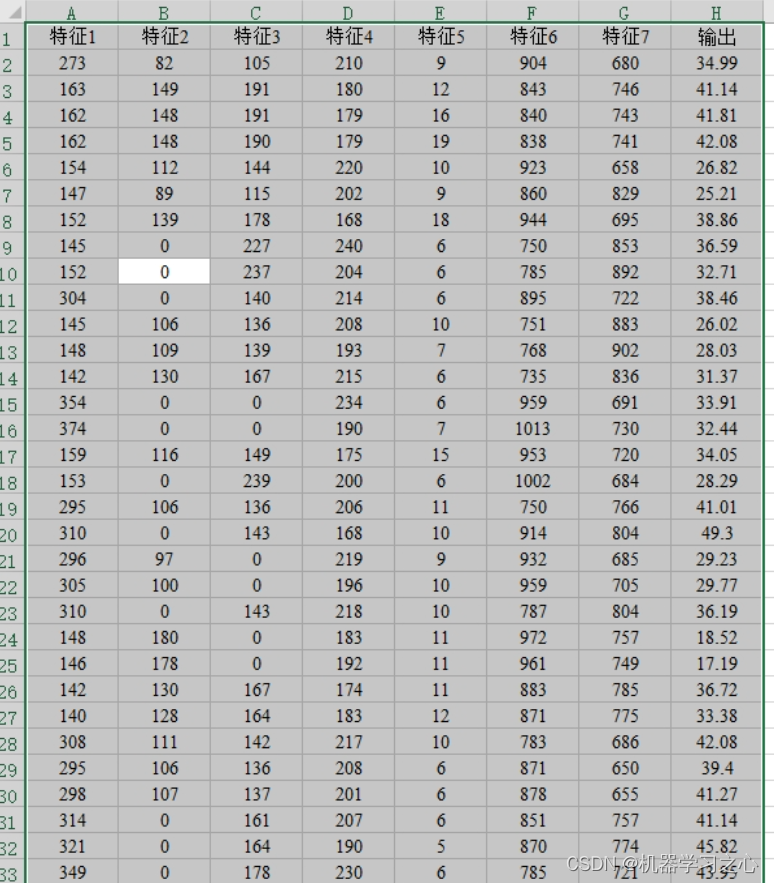
回归预测 | Matlab实现POA-BP鹈鹕算法优化BP神经网络多变量回归预测
回归预测 | Matlab实现POA-BP鹈鹕算法优化BP神经网络多变量回归预测 目录 回归预测 | Matlab实现POA-BP鹈鹕算法优化BP神经网络多变量回归预测预测效果基本描述程序设计参考资料 预测效果 基本描述 1.Matlab实现POA-BP鹈鹕算法优化BP神经网络多变量回归预测(完整源码…...
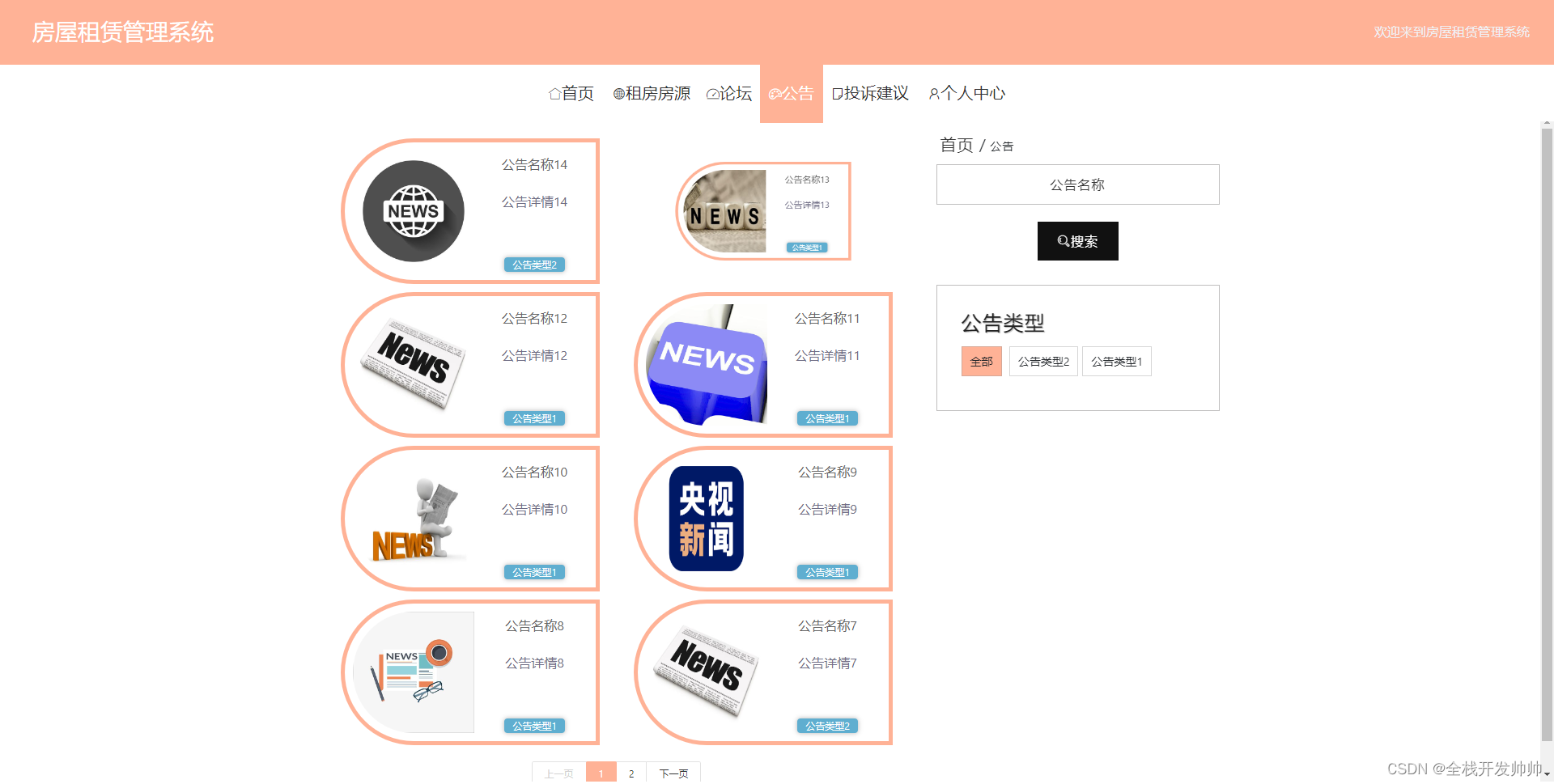
基于java+springboot+vue实现的房屋租赁管理系统(文末源码+Lw)23-142
第1章 绪论 房屋租赁管理系统管理系统按照操作主体分为管理员和用户。管理员的功能包括报修管理、字典管理、租房房源管理、租房评价管理、房源租赁管理、租房预约管理、论坛管理、公告管理、投诉建议管理、用户管理、租房合同管理、管理员管理。用户的功能等。该系统采用了My…...
ubuntu20安装mongodb
方法一:直接安装(命令是直接从mongo官网Install MongoDB Community Edition on Ubuntu — MongoDB Manual复制的) cat /etc/lsb-release sudo apt-get install -y gnupg curl curl -fsSL https://www.mongodb.org/static/pgp/server-7.0.asc | \sudo gp…...

java面试题:MySQL中的各种JOIN的区别
表关联是频率非常高的一种数据库操作,在MySQL中,这种JOIN操作有很多类型,包括内联接、左外连接、右外连接等等,而每种连接的含义都不一样,如果死记硬背,不仅很难记住,而且也容易搞混淆ÿ…...
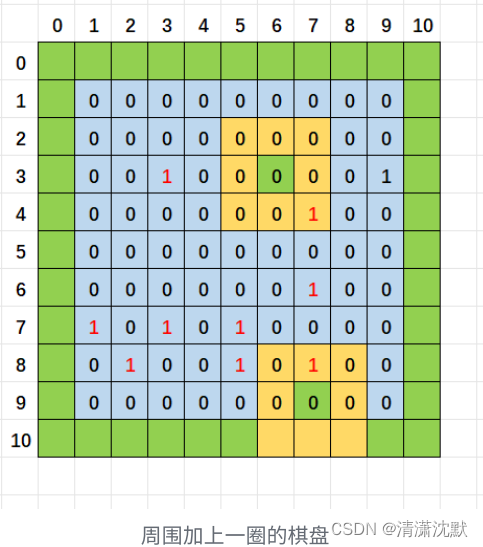
C语言数组与扫雷游戏实现(详解)
扫雷游戏的功能说明 使⽤控制台实现经典的扫雷游戏游戏可以通过菜单实现继续玩或者退出游戏扫雷的棋盘是9*9的格子默认随机布置10个雷可以排查雷 ◦ 如果位置不是雷,就显示周围有几个雷 ◦ 如果位置是雷,就炸死游戏结束 ◦ 把除10个雷之外的所有雷都找出来,排雷成功,游戏结…...

C#调用WechatOCR.exe实现本地OCR文字识别
最近遇到一个需求:有大量的扫描件需要还原为可编辑的文本,很显然需要用到图片OCR识别为文字技术。本来以为这个技术很普遍的,结果用了几个开源库,效果不理想。后来,用了取巧的方法,直接使用了WX的OCR识别模…...

ComfyUI 学习笔记
目录 ComfyUI 入门教程 什么是ComfyUI? windows安装教程: 组件技巧学习 ComfyUI 入门教程 老V带你学comfyUI-基础入门 - 知乎 什么是ComfyUI? ComfyUI 是一个基于节点的 GUI,用于Stable Diffusion。你可以通过将不同的no…...

基于Linux的HTTP代理服务器搭建与配置实战
在数字化世界中,HTTP代理服务器扮演着至关重要的角色,它们能够帮助我们管理网络请求、提高访问速度,甚至在某些情况下还能保护我们的隐私。而Linux系统,凭借其强大的功能和灵活性,成为了搭建HTTP代理服务器的理想选择。…...
创建一个Vue项目(含npm install卡住不动的解决)
目录 1 安装Node.js 2 使用命令提示符窗口创建Vue 2.1 打开命令提示符窗口 2.2 初始Vue项目 2.2.1 npm init vuelatest 2.2.2 npm install 3 运行Vue项目 3.1 命令提示符窗口 3.2 VSCode运行项目 1 安装Node.js 可以看我的这篇文章《Node.js的安装》 2 使用命令提示…...

npm_config_xxx
// package.json{ "scripts": { "log": "node index.js", } }// index.js function logProcessEnv(key){ console.log(process.env[${key}], process.env[key]); } logProcessEnv(npm_config_foo); 问题: npm run log 和 yarn log…...

P8756 [蓝桥杯 2021 省 AB2] 国际象棋 状压dp统计情况数的一些小理解
目录 建议有状压基础再食用:本题的状态转移方程是 dp代码片:参考代码 建议有状压基础再食用: n行m列 等价 n列m行 ,因为n比较小,int是32位足够了,我们用比特位统计每一行的状态。 本题的状态转移方程是 dp[h][i][j]…...
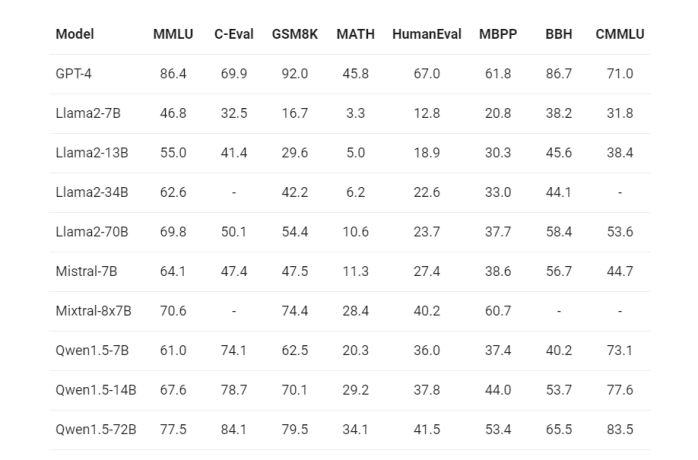
春节放大招,阿里通义千问Qwen1.5开源发布
2月6日阿里发布了通义千问1.5版本,包含6个大小的模型,“Qwen” 指的是基础语言模型,而 “Qwen-Chat” 则指的是通过后训练技术如SFT(有监督微调)和RLHF(强化学习人类反馈)训练的聊天模型。 模型…...
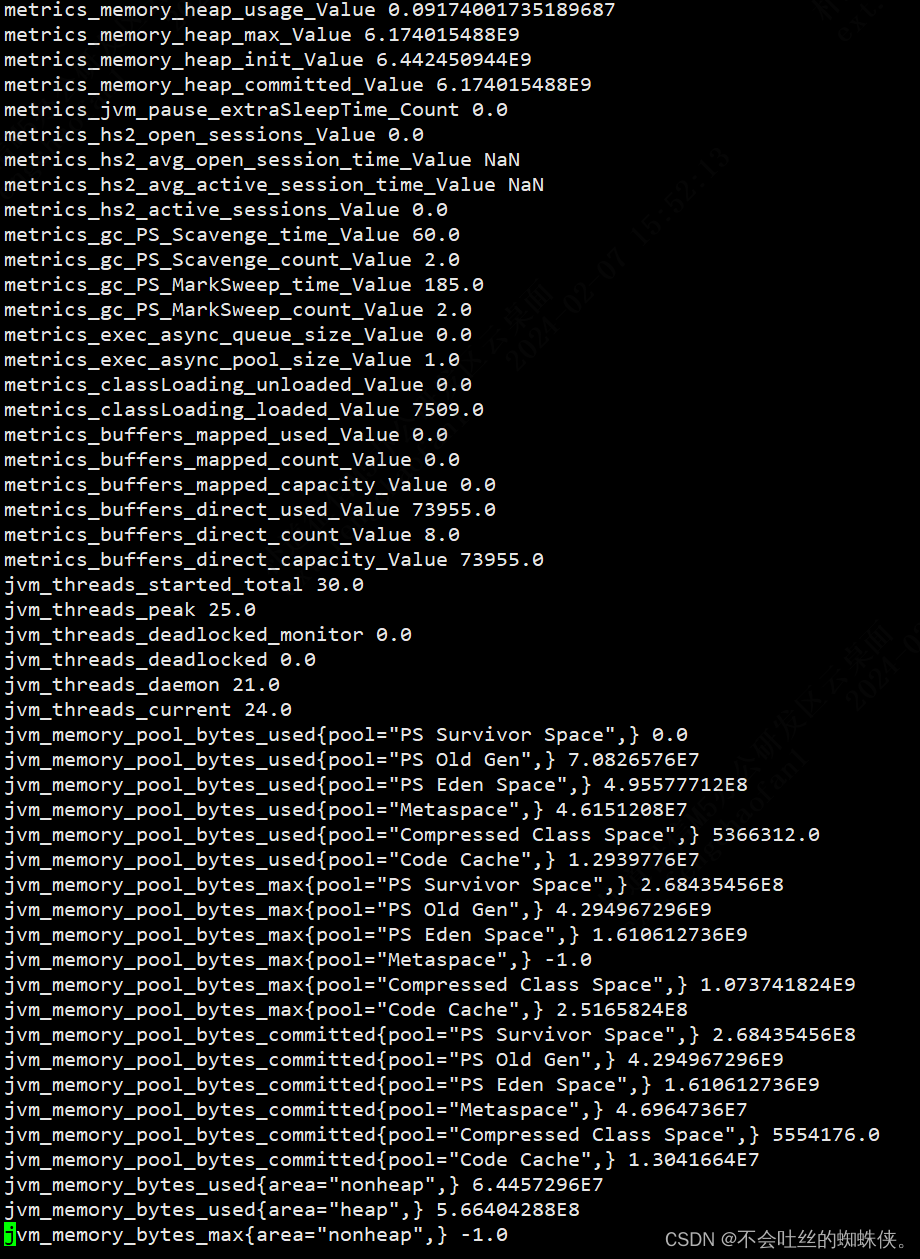
grafana+prometheus+hiveserver2(jmx_exporter+metrics)
一、hiveserver2开启metrics,并启动jmx_exporter 1、修改hive-site.xml文件开启metrics <property><name>hive.server2.metrics.enabled</name><value>true</value> </property> <property><name>hive.service.m…...

Redis系列——Lua脚本和redis事务的应用
介绍 Lua脚本 背景 Redis是一种抽象数据类型的特定领域语言,由各种命令组成。大多数命令专门用于操作不通的数据类型。每次发送命令均需要执行至此网络请求。所以Redis提供了一个编程接口,支持服务器执行用户自定义的任意脚本。有助于减少网络流量&am…...

rtt设备驱动框架面向对象学习-i2c总线
本来想着i2c和spi是一样的,标题都想抄袭成《rtt设备驱动框架学习-i2c总线和设备》,然后看过源码发现,i2c没有分开总线和设备,我想着正常它和spi一样有总线和设备,设备存在竞争。估计是因为i2c设备可以通过i2c地址区分&…...

Golang 基础 Go Modules包管理
Golang 基础 Go Modules包管理 在 Go 项目开发中,依赖包管理是一个非常重要的内容,依赖包处理不好,就会导致编译失败,本文将系统介绍下 Go 的依赖包管理工具。 我会首先介绍下 Go 依赖包管理工具的历史,并详细介绍下…...
)
图数据库 之 Neo4j - 背景介绍(1)
引言 Neo4j是一种高性能的图数据库,它专门设计用于存储、管理和查询大规模的图数据。与传统的关系型数据库不同,Neo4j以图的形式存储数据,其中节点表示实体,边表示实体之间的关系。这种图数据模型非常适合表示复杂的关系和连接。…...

JAVA中的单例模式->饿汉式
一、步骤 1.构造器私有化>防止直接new // 步骤一、构造器私有化>防止直接new private GirlFriend(String name){System.out.println("构造器被调用");this.name name; } 2.类的内部创建对象 // 步骤二、类的内部创建对象(该对象是static&#x…...
从零开始手写mmo游戏从框架到爆炸(三)— 服务启动接口与网络事件监听器
导航:从零开始手写mmo游戏从框架到爆炸(零)—— 导航-CSDN博客 上一章我们完成了netty服务启动的相关抽象(https://blog.csdn.net/money9sun/article/details/136025471),这一章我们再新增一个全…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
