鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Span组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Span组件
一、操作环境
操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1+

二、Span组件
鸿蒙(HarmonyOS)作为Text组件的子组件,用于显示行内文本的组件。
子组件
无。
接口
Span(value: string | Resource)
从API version 9开始,该接口支持在ArkTS卡片中使用。
参数
| 参数名 | 参数类型 | 必填 | 参数描述 |
|---|---|---|---|
| value | string | Resource | 是 | 文本内容。 |
属性
通用属性方法仅支持通用文本样式。
| 名称 | 参数类型 | 描述 |
|---|---|---|
| decoration | { type: TextDecorationType, color?: ResourceColor } | 设置文本装饰线样式及其颜色。 默认值:{ type: TextDecorationType.None color:Color.Black } 从API version 9开始,该接口支持在ArkTS卡片中使用。 |
| letterSpacing | number | string | 设置文本字符间距。取值小于0,字符聚集重叠,取值大于0且随着数值变大,字符间距越来越大,稀疏分布。 从API version 9开始,该接口支持在ArkTS卡片中使用。 |
| textCase | TextCase | 设置文本大小写。 默认值:TextCase.Normal 从API version 9开始,该接口支持在ArkTS卡片中使用。 |
事件
通用事件仅支持点击事件。
说明
由于Span组件无尺寸信息,因此点击事件返回的ClickEvent对象的target属性无效。
示例
代码
// xxx.ets
@Entry
@Component
struct SpanExample {build() {Flex({ direction: FlexDirection.Column, alignItems: ItemAlign.Start, justifyContent: FlexAlign.SpaceBetween }) {Text('Basic Usage').fontSize(9).fontColor(0xCCCCCC)Text() {Span('In Line')Span(' Component')Span(' !')}Text() {Span('This is the Span component').fontSize(12).textCase(TextCase.Normal).decoration({ type: TextDecorationType.None, color: Color.Red })}// 文本横线添加Text('Text Decoration').fontSize(9).fontColor(0xCCCCCC)Text() {Span('I am Underline-span').decoration({ type: TextDecorationType.Underline, color: Color.Red }).fontSize(12)}Text() {Span('I am LineThrough-span').decoration({ type: TextDecorationType.LineThrough, color: Color.Red }).fontSize(12)}Text() {Span('I am Overline-span').decoration({ type: TextDecorationType.Overline, color: Color.Red }).fontSize(12)}// 文本字符间距Text('LetterSpacing').fontSize(9).fontColor(0xCCCCCC)Text() {Span('span letter spacing').letterSpacing(0).fontSize(12)}Text() {Span('span letter spacing').letterSpacing(-2).fontSize(12)}Text() {Span('span letter spacing').letterSpacing(3).fontSize(12)}// 文本大小写展示设置Text('Text Case').fontSize(9).fontColor(0xCCCCCC)Text() {Span('I am Lower-span').fontSize(12).textCase(TextCase.LowerCase).decoration({ type: TextDecorationType.None })}Text() {Span('I am Upper-span').fontSize(12).textCase(TextCase.UpperCase).decoration({ type: TextDecorationType.None })}}.width('100%').height(250).padding({ left: 35, right: 35, top: 35 })}
}图例

你有时间常去我家看看我在这里谢谢你啦...
我家地址:亚丁号
最后送大家一首诗:
山高路远坑深,
大军纵横驰奔,
谁敢横刀立马?
惟有点赞加关注大军。
相关文章:

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Span组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Span组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、Span组件 鸿蒙(HarmonyOS)作为Text组件的子组件࿰…...
Leetcode—42. 接雨水【困难】
2024每日刷题(112) Leetcode—42. 接雨水 空间复杂度为O(n)的算法思想 实现代码 class Solution { public:int trap(vector<int>& height) {int ans 0;int n height.size();vector<int> l(n);vector<int> r(n);for(int i 0; …...
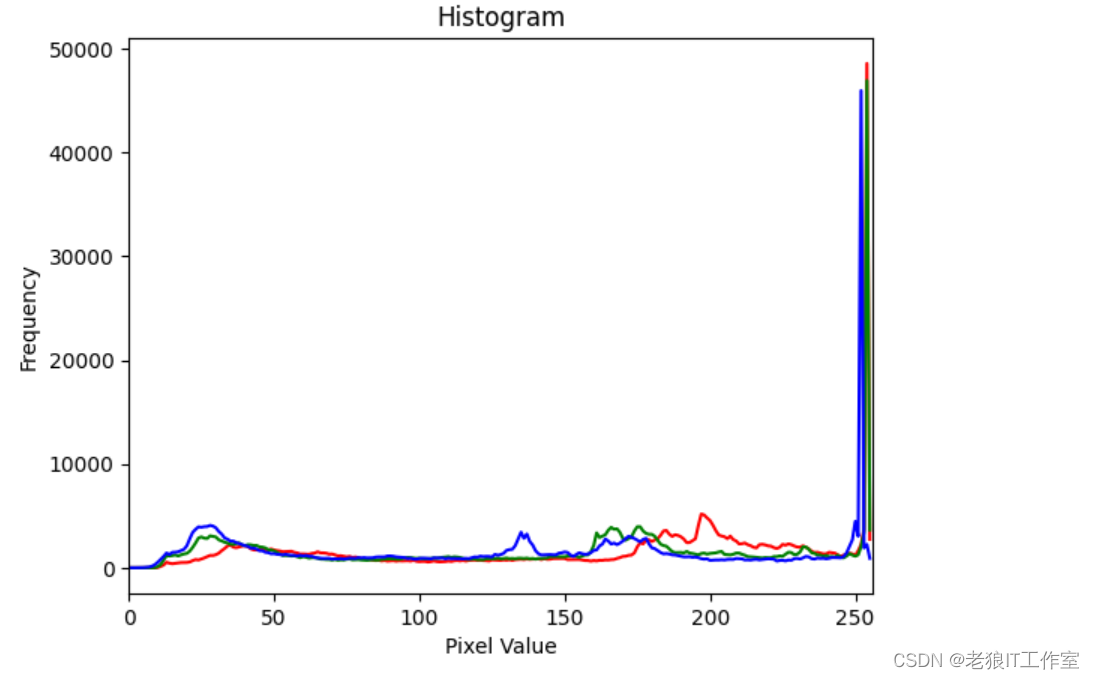
[Python] opencv - 什么是直方图?如何绘制图像的直方图?如何对直方图进行均匀化处理?
什么是直方图? 直方图是一种统计图,用于展示数据的分布情况。它将数据按照一定的区间或者组进行划分,然后计算在每个区间或组内的数据频数或频率(即数据出现的次数或占比),然后用矩形或者柱形图的形式将这…...

ppi rust开发 python调用
创建python的一个测试工程 python -m venv venv .\venv\Scripts\activatepip install cffi创建一个rust的lib项目 cargo new --lib pyrustlib.rs #[no_mangle] pub extern "C" fn rust_add(x: i32, y: i32) -> i32 {x y }Cargo.toml [package] name "p…...
)
网站后端开发 thinkphp6 入门教程合集(更新中)
thinkphp6 入门(1)--安装、路由规则、多应用模式 thinkphp6 入门(1)--安装、路由规则、多应用模式_软件工程小施同学的博客-CSDN博客 thinkphp6 入门(2)--视图、渲染html页面、赋值 thinkphp6 入门&#x…...
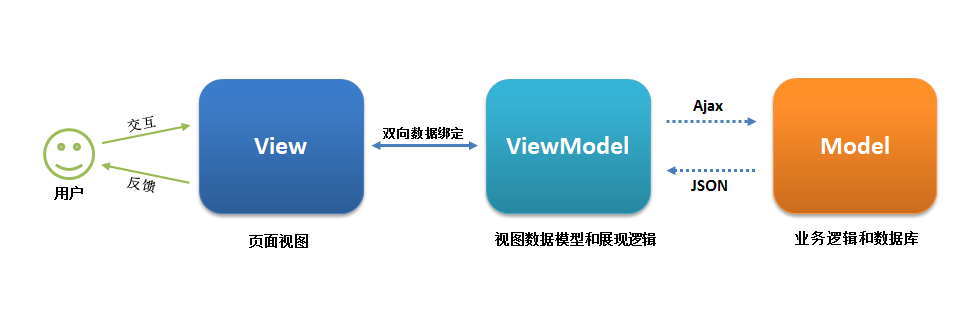
Web前端框架-Vue(初识)
文章目录 web前端三大主流框架**1.Angular****2.React****3.Vue**什么是Vue.js 为什么要学习流行框架框架和库和插件的区别一.简介指令v-cloakv-textv-htmlv-pre**v-once**v-onv-on事件函数中传入参数事件修饰符双向数据绑定v-model 按键修饰符自定义按键修饰符别名v-bind(属性…...
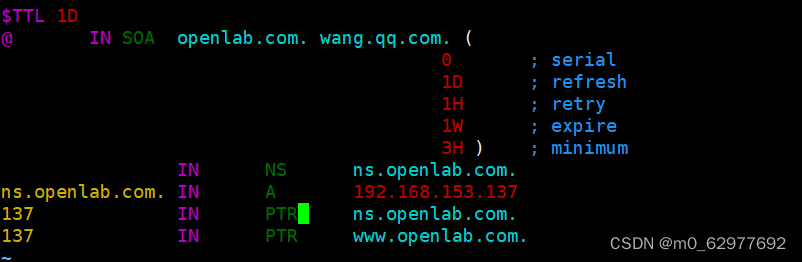
配置dns服务的正反向解析
服务端IP客户端IP网址192.168.153.137192.168.153.www.openlab.com 1:正向解析 1.1关闭客户端和服务端的安全软件,安装bind软件 [rootserver ~]# setenforce 0 [rootserver ~]# systemctl stop firewalld [rootserver ~]# yum install bind -y [rootnod…...

小白水平理解面试经典题目LeetCode 71. Simplify Path【Stack类】
71. 简化路径 小白渣翻译 给定一个字符串 path ,它是 Unix 风格文件系统中文件或目录的绝对路径(以斜杠 ‘/’ 开头),将其转换为简化的规范路径。 在 Unix 风格的文件系统中,句点 ‘.’ 指的是当前目录,…...
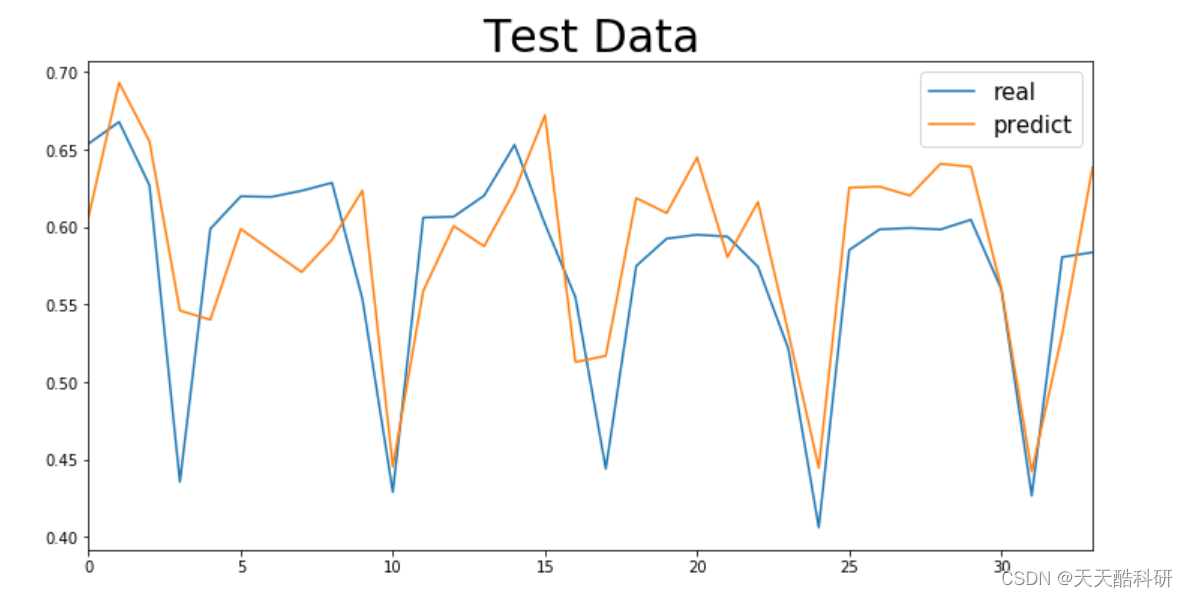
电力负荷预测 | 电力系统负荷预测模型(Python线性回归、随机森林、支持向量机、BP神经网络、GRU、LSTM)
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 电力系统负荷预测模型(Python线性回归、随机森林、支持向量机、BP神经网络、GRU、LSTM) 所谓预测,就是指通过对事物进行分析及研究,并运用合理的方法探索事物的发展变化规律,对其未来发展做出预先估计和判断。…...

YY调音台:音频后期处理
我从事影视后期处理的工作,主要负责音频、音效合成这块工作内容。在影视作品中,声音不仅仅是背景元素,它在叙事和创造情感氛围上发挥着至关重要的作用。我们的工作不仅要让听众听到声音,更要让他们通过声音感受到情感的波动和故事…...

一键部署一个监控系统hertzbeat
效果 特点 一站式监控告警通知,支持应用服务,数据库,操作系统,中间件,云原生,网络等。 易用友好,无需 Agent,全页面操作,鼠标点一点就能监控告警。 强大监控模版能力&…...
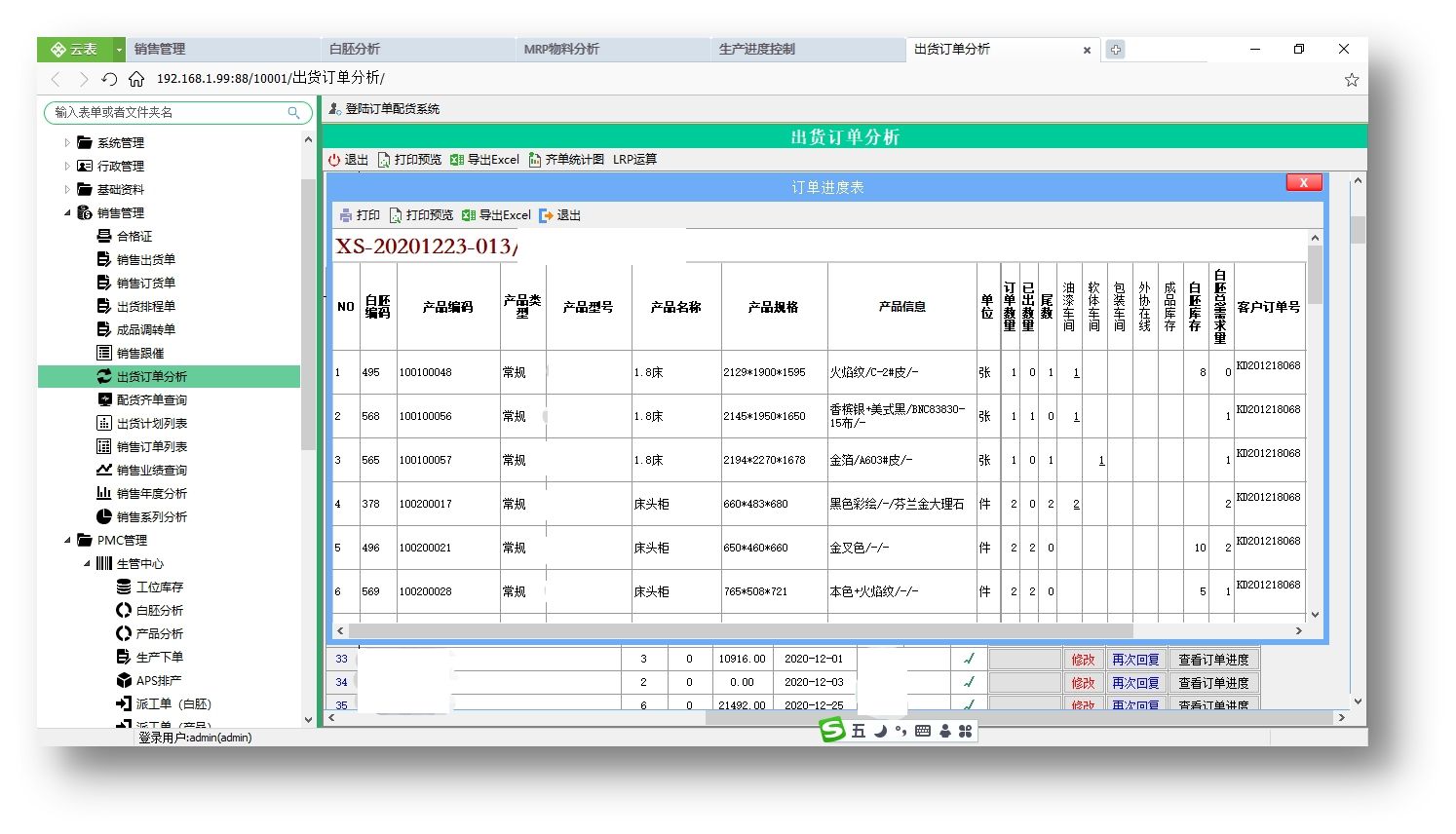
为电子表格嵌入数据库,Excel/WPS一键升级为管理系统
将Excel表格转化为管理系统,这款工具能够实现只需导入表格数据,即可自动生成相应的软件和APP。 表格办公的烦恼,有遇到吧? 对于具有一定规模的企业而言,各类表格如同繁星般众多,既有日常使用的常规表格&a…...
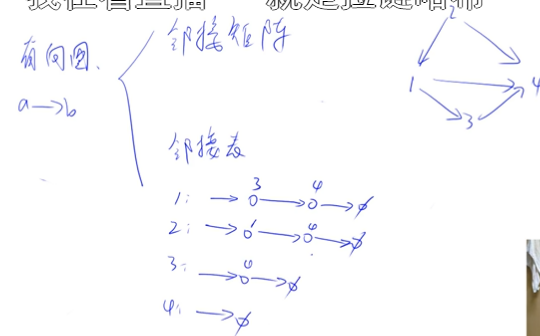
搜索与图论(一)(深搜,广搜,树与图的存储遍历,拓扑排序)
一、DFS 往深里搜,搜到叶子结点那里,回溯,到可以继续到叶子结点深搜的位置。 1、回溯一定要恢复现场 2、定义一个与当前递归层数有关的终止条件(题目要求的东西) 3、每层都用循环判断是否存在可以dfs的路 输出数字…...

【开源】基于JAVA+Vue+SpringBoot的停车场收费系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 停车位模块2.2 车辆模块2.3 停车收费模块2.4 IC卡模块2.5 IC卡挂失模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 停车场表3.2.2 车辆表3.2.3 停车收费表3.2.4 IC 卡表3.2.5 IC 卡挂失表 四、系统实现五、核心代码…...
DDoS攻击激增,分享高效可靠的DDoS防御方案
当下DDoS攻击规模不断突破上限,形成了 "网络威胁格局中令人不安的趋势"。专业数据显示,对比2022年上半年与2023年上半年,所有行业的DDoS攻击频率增加了314%。其中零售、电信和媒体公司遭受的攻击规模最大,三个垂直行业的…...

打卡今天学习的命令 (linux
1.1 cp - 复制文件或目录 cp source destination cp -r source_directory destination # 递归复制目录及其内容1.2 rm - 删除文件或目录 rm file rm -r directory # 递归删除目录及其内容1.3 mv - 移动/重命名文件或目录 mv source destination mv old_name new_name # 重…...

[C#]无法获取源 https://api.nuge t.org/v3-index存储签名信息解决方法
参考网上大部分方法错误,根本不起作用。正确方法是 C:\Users\你的用户名\AppData\Roaming\NuGet找到NuGet.Config打开,看到类似下面信息(可能不一样) <?xml version"1.0" encoding"utf-8"?> <co…...

FRP内网穿透如何避免SSH暴力破解(二)——指定地区允许访问
背景 上篇文章说到,出现了试图反复通过FRP的隧道,建立外网端口到内网服务器TCP链路的机器人,同时试图暴力破解ssh。这些连接造成了流量的浪费和不必要的通信开销。考虑到服务器使用者主要分布在A、B、C地区和国家,我打算对上一篇…...

Unity类银河恶魔城学习记录4-1,4-2 Attack Logic,Collider‘s collision excepetion源代码 P54 p55
Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili Entity.cs using System.Collections; using System.Collections.Generic; u…...

各种编程语言送祝福:2024龙年大吉
我是码农一枚,在这里用不同编程语言中祝福大家"2024,龙年大吉"~ Python print("2024,龙年大吉")Java public class Main {public static void main(String[] args) {System.out.println("2024,龙年大…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
