算法学习打卡day47|单调栈系列题目
单调栈题目思路
- 通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。时间复杂度为O(n)。
- 单调栈的本质是空间换时间,因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素,优点是整个数组只需要遍历一次。
单调栈解题步骤
- 建立一个栈,然后从头遍历元素。
- 既然为单调栈,那么肯定分为单调递增栈和单调递减栈(这里的单调递增或者递减指的是从栈顶到栈底方向),这里单调栈递增(从栈口到栈底顺序),就是求右边第一个比自己大的,单调栈递减的话,就是求右边第一个比自己小的。 那么分为两种情况:
- 如果是单调递增栈时,当栈为空或者当前元素值小于栈顶元素时,执行push操作,此时的栈从栈顶到栈底为单调递增,而当前元素值大于栈顶元素值时,不符合单调递增,此时当前元素就是栈顶元素的右侧第一个比它大的元素,输出结果即可(注意这里要循判断栈顶元素是否都符合情况),当然左侧比自己大的元素就是当前栈顶的下一个元素了。
- 如果是单调递减栈时,同样的思路,当栈为空或者当前元素值大于栈顶元素时,执行push操作,此时的栈从栈顶到栈底为单调递减,而当前元素值小于栈顶元素值时,不符合单调递减,此时当前元素就是栈顶元素的右侧第一个比它小的元素,输出结果即可(注意这里要循判断栈顶元素是否都符合情况),当然左侧比自己小的元素就是当前栈顶的下一个元素了(接雨水和求柱子最大面积会用)。
- 注意:
- 这里其实在元素等于栈顶元素的时候可以和另一个步骤合并,而不影响计算结果。
- 单调栈解题,一般都是存数组下标,数组元素可以下标访问,很方便。
每日温度
力扣题目链接
题目描述:
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
思路:
- 从题目可以直接看到要求下一个更高温度在几天后,很显然就是求右边第一个比自己大的元素位置减去当前位置下标即位所求,直接使用单调栈来解题,很显然这道题时单调递增栈(从栈顶到栈底)。
代码实现:
class Solution {
public:vector<int> dailyTemperatures(vector<int>& temperatures) {vector<int> result(temperatures.size(), 0);stack<int> stk;for (int i = 0; i < temperatures.size(); ++i) {while (!stk.empty() && temperatures[i] > temperatures[stk.top()]) {int tmp = stk.top();result[tmp] = i - tmp;stk.pop();}stk.push(i);}return result; }
};
下一个最大元素一
力扣题目链接
题目描述:
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
思路:
- 本题和每日温度类似,但是是在另一个数组里找,其实是一样的,我们可以用一个哈希map记录nums1的元素和下标映射关系,然后通过单调栈的方式去找nums2中每个元素的右侧最大值,当遇到符合条件的时候,就到map里找一下是否存在nums2里的这个元素,存在的话,就对应输出即可。
代码实现:
class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {vector<int> result(nums1.size(), -1);unordered_map<int, int> map;for (int i = 0; i < nums1.size(); ++i) {map.insert(pair<int, int>{nums1[i], i});}stack<int> stk;for (int i = 0; i < nums2.size(); ++i) {//int num = nums2[i];while (!stk.empty() && nums2[i] > stk.top()) {if (map.count(stk.top())) {result[map[stk.top()]] = nums2[i];}stk.pop();}stk.push(nums2[i]);}return result;}
};
下一个最大元素二
力扣题目链接
题目描述:
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
示例 2:
输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]
思路:
- 和上一个题类似,但是这次是循环数组,那么一般遇到循环数组的时候,我们没必要去把原数组拼接一次,直接让下标可以增长到2*n即可,在访问元素的时候对下标取余操作就不会越界。
- 其他步骤就是单调栈的解题模板,注意这里可以剪枝一下,如果第一轮已经处理过的就不用再push一次了,没处理过的push即可。
代码实现:
class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {int n = nums.size();stack<int> stk;vector<int> result(n, -1);for (int i = 0; i < 2 * n; ++i) {//上界为2n时,循环的时候模拟循环数组while (!stk.empty() && nums[i % n] > nums[stk.top()]) {result[stk.top()] = nums[i % n];stk.pop();}if (result[i % n] == -1) stk.push(i % n);//剪枝,之前已经处理过的可以不用push了。}return result;}
};
接雨水
力扣题目链接
题目描述:
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
思路:
- 题目解读:若干个柱子,用凹槽去接雨水,这里是去求凹槽的面积之和,有两种思路:
-
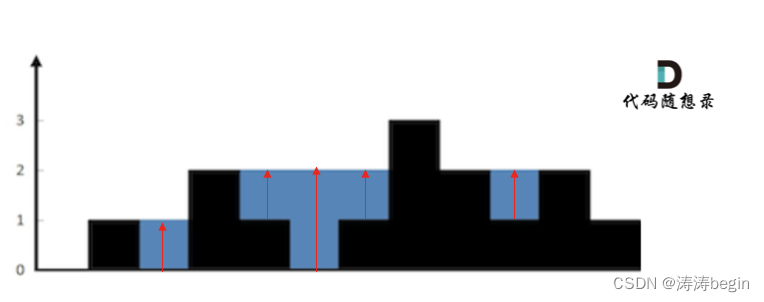
按列计算(暴力解法),遍历每个元素,求出该元素能接的雨水高度,然后求和,这种情况需要分别求左右两侧比自己高的元素中的最大值,比如下图中的第6列,左侧比自己高的的最高柱子为第4列,右侧是第8列,那么第6列接雨水的高度就是第4列和第8列中高度较小的那个,这里是2。
-
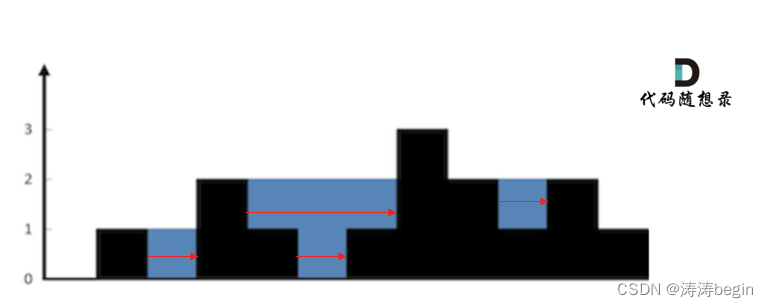
按行计算(单调栈解法),找出两边第一个比自己高的柱子,然后求出宽度,高度是两边柱子中的最小值减去当前柱子高度,比如还是第6列,此时左右两侧第一个比自己高的是第5和第7列,那么此时宽度就是
7 - 5 - 1 = 1,高度是两者的最小值减去第6列的高度:1 - 0 = 1,这里两侧的高度刚好相等了,而如果是第5列的话,那么左右两侧分别是第4和第8列,那么宽度为8 - 4 - 1 = 3,高度为两者的最小值减去第5列的高度:2 - 1 = 1,然后面积就是高度宽度相乘。
代码实现
-
- 暴力解法(时间复杂度为 O ( n 2 ) O(n^2) O(n2),力扣无法通过):
class Solution {
public:int trap(vector<int>& height) {int sum = 0;int lhigh = 0, rhigh = 0;for (int i = 1; i < height.size() - 1; ++i) {//找左边比它大的lhigh = height[i], rhigh = height[i];for (int j = i - 1; j >= 0; --j) {if (height[j] >= lhigh) {//注意这里找的是左边最大的那个,所以一直和lhigh比较lhigh = height[j];}}//找右边比它大的for (int k = i + 1; k < height.size(); ++k) {if (height[k] >= rhigh) {//注意这里找的是右边最大的那个,所以一直和rhigh比较rhigh = height[k];}}sum += min(rhigh, lhigh) - height[i];}return sum;}
};
- 暴力解法优化:其实在找左右两侧最大值的时候有很多重复比较,我们其实直接取前面一个元素的结果和当前值做比较即可((为什么和当前值比较?如果没有比自己大的,就用当前值,那么算的时候高度差为0,就没有高度无法接雨水了)),在遍历数组之前,先把左右两侧比自己高的最大值找出来。
class Solution {
public:int trap(vector<int>& height) {int sum = 0;vector<int> l_max_vec(height.size(), 0);vector<int> r_max_vec(height.size(), 0);//直接把每个位置的左侧最高柱子都计算出来l_max_vec[0] = height[0];for (int i = 1; i < height.size(); ++i) {l_max_vec[i] = max(l_max_vec[i - 1], height[i]);}//直接把每个位置的右侧最高柱子都计算出来r_max_vec[height.size() - 1] = height[height.size() - 1];for (int j = height.size() - 2; j >= 0; --j) {r_max_vec[j] = max(r_max_vec[j + 1], height[j]);}//循环一次,直接计算即可。for (int i = 1; i < height.size() - 1; ++i) { sum += min(l_max_vec[i], r_max_vec[i]) - height[i];}return sum;}
};
- 单调栈解法(按行求解):
class Solution {
public:int trap(vector<int>& height) {stack<int> stk;int sum = 0;for (int i = 0; i < height.size(); ++i) {while (!stk.empty() && height[i] > height[stk.top()]) {int cur = stk.top();stk.pop();if (stk.empty()) break;int next = stk.top();//前面比它高的int high = min(height[i], height[next]) - height[cur];//高度差int weight = i - next - 1;//宽度sum += high * weight;//面积}stk.push(i);/*这里可以剪枝,如果相邻两个柱子高度相同算一个就行了,因为即使放进去,high计算的时候也是0*/}return sum;}
};
柱状图中最大的矩形
力扣题目链接
题目描述:
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
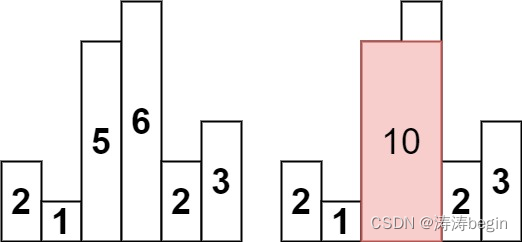
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:
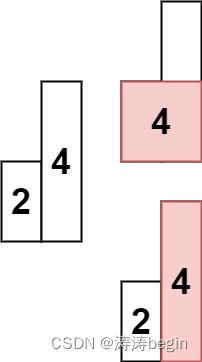
输入: heights = [2,4]
输出: 4
思路:
- 和接雨水类似,但是本题更加复杂,接雨水是求凹槽,相当于是柱子外,本题是求柱子内的最大面积,**既然是求最大面积,那么本题需要找到的是每个柱子的左右两侧的第一个比自己小的那个柱子(注意这个题和前面四道题不一样了!!!,是求左右两侧比自己小的柱子,此时为栈顶到栈底单调递减),**这样的话用得到的宽度和当前柱子高度相乘即为已当前柱子为高度的矩形面积,然后依次对每个柱子求矩形面积取最大值即可。
- 暴力解法:和接雨水不太一样,本题是找到左右两侧第一个比自己小的柱子(不再是找最小的柱子了(接雨水是找最大的柱子))
- 注意:
- 如果数组本身单调递增的话,那么入栈后整体呈现单调递减就找不到右侧比自己小的元素了,这种情况对于接雨水来说不用特殊处理(没有凹槽,雨水为0),但是本题不行,可以直接在原数组尾部加一个0,这样既不影响结果,也能找到了右侧比自己小的元素。
- 对于数组单调递减的情况不用在数组开头添加元素,直接让left的高度设为-1即可。
代码实现
- 单调栈解法:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int result = 0;stack<int> stk;heights.push_back(0);//单独处理,尾部加0for (int i = 0; i < heights.size(); ++i) {while (!stk.empty() && heights[i] < heights[stk.top()]) {int top = stk.top();stk.pop();int left = -1;//单独处理,left设为-1if (!stk.empty()) left = stk.top();int weight = i - left - 1;int s = heights[top] * weight;result = max(result, s);}stk.push(i);}return result;}
};
- 暴力解法:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int result = INT_MIN;for (int i = 0; i < heights.size(); ++i) {int l_min = -1, r_min = heights.size();for (int j = i - 1; j >= 0; --j) {if (heights[j] < heights[i]) {l_min = j;break;}}for (int k = i + 1; k < heights.size(); ++k) {if (heights[k] < heights[i]) {r_min = k;break;} }//cout << l_min << " " << r_min << endl;int weight = r_min - l_min - 1;int s = weight * heights[i];result = result > s ? result : s;}return result;}
};
- 暴力解法优化:和接雨水优化类似,但是此处需要在for循环里用while循环去不断找到小于cur的柱子。(注意遇到等于的时候也要继续去找,当然也可以把等于逻辑拿出来单独写,其实是一样的)
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int result = INT_MIN;vector<int> l_min_vec(heights.size(), -1);//默认没有比当前柱子小的vector<int> r_min_vec(heights.size(), heights.size());//默认没有比当前柱子小的//求左侧第一个小于当前高度的柱子for (int i = 1; i < heights.size(); ++i) {int t = i - 1;while (t >= 0 && heights[t] >= heights[i]) {t = l_min_vec[t];}//大于一直往左走l_min_vec[i] = t;//直到遍历到头或者小于的时候}//求右侧第一个小于当前高度的柱子for (int j = heights.size() - 2; j >= 0; --j) {int t = j + 1;while (t < heights.size() && heights[t] >= heights[j]) {t = r_min_vec[t];}//大于等于一直往右走r_min_vec[j] = t;//直到遍历到头或者小于的时候}//求面积for (int i = 0; i < heights.size(); ++i) {int weight = r_min_vec[i] - l_min_vec[i] - 1;int s = weight * heights[i];result = max(s, result);}return result;}
};
总结
- 单调栈题目大体模版都是一样的,就是while里的处理逻辑可能不同,可以先熟悉暴力解法,然后看看和单调栈解法的区别在哪,妙在哪里。
相关文章:

算法学习打卡day47|单调栈系列题目
单调栈题目思路 通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。时间复杂度为O(n)。单调栈的本质是空间换时间,因为在遍历的过程中需要用一个栈来记录右边第一个比当前元…...
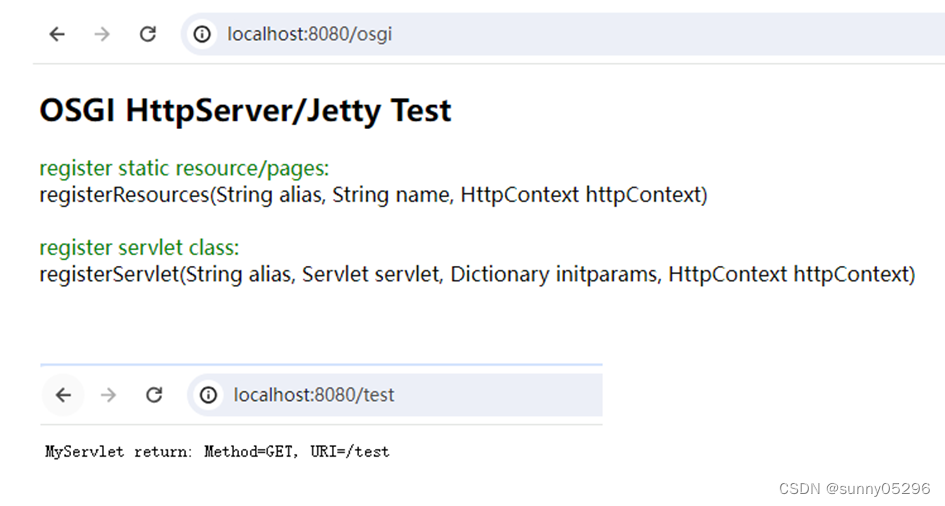
Maven构建OSGI+HttpServer应用
Maven构建OSGIHttpServer应用 官网(https://eclipse.dev/equinox/server/http_in_equinox.php)介绍有两种方式: 一种是基于”org.eclipse.equinox.http”包的轻量级实现,另一种是基于”org.eclipse.equinox.http.jetty”包&#…...

chrome扩展插件常用文件及作用
Chrome扩展通常包含以下常用文件及其作用: manifest.json: 描述了扩展的基本信息,如名称、版本、权限、图标等。定义了扩展的各种组件和功能,包括后台脚本、内容脚本、页面、浏览器动作按钮等。 background.js: 后台脚…...

PdfFactory Pro软件下载以及序列号注册码生成器
PdfFactory Pro注册机是一款针对同名虚拟打印机软件所推出的用户名和序列号生成器。PdfFactory Pro是一款非常专业的PDF虚拟打印软件,通过使用这款注册机,就能帮助用户免费获取注册码,一键激活,永久免费使用。 pdffactory7注册码如…...
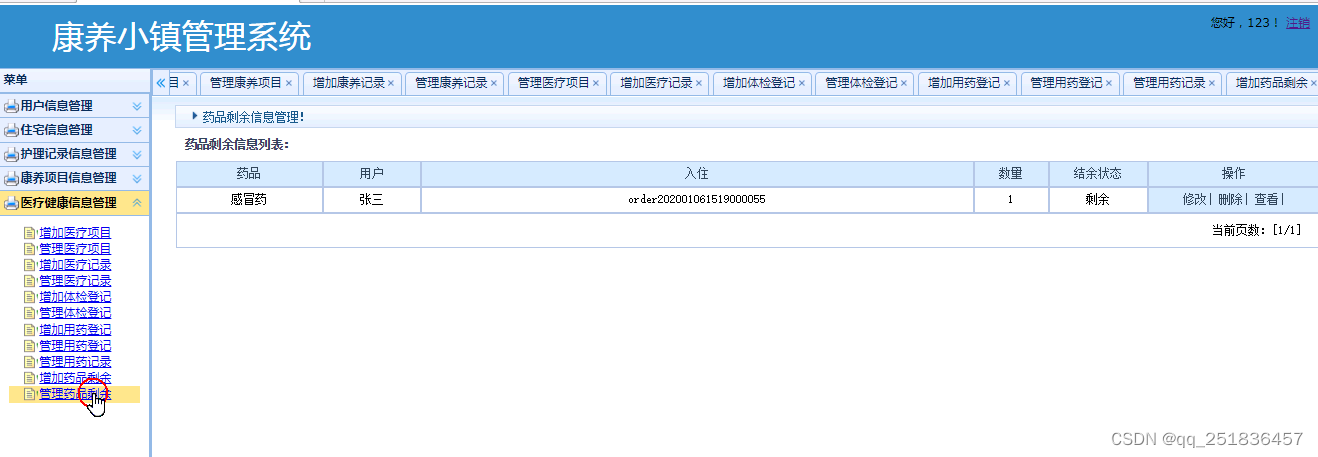
jsp康养小镇管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 JSP康养小镇管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&a…...

Android 无操作之后定时退出
android定时器监用户听对页面无操作5分钟退出登录实现 - 简书 private long advertisingTime 600000;///定时结束退出登录10分(分钟)600000毫秒public CountDownTimer countDownTimer;Overrideprotected void onResume() {super.onResume();//启动定时if (isTimedExitApp()) …...
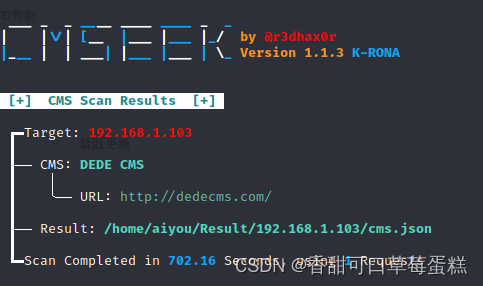
CMS 检测神器:CMSeek 保姆级教程(附链接)
一、介绍 CMSeek(Content Management System Exploitation and Enumeration Toolkit)是一款用于检测和利用网站上可能存在的内容管理系统(CMS)漏洞的开源工具。它旨在帮助安全研究人员和渗透测试人员识别目标网站所使用的CMS&…...
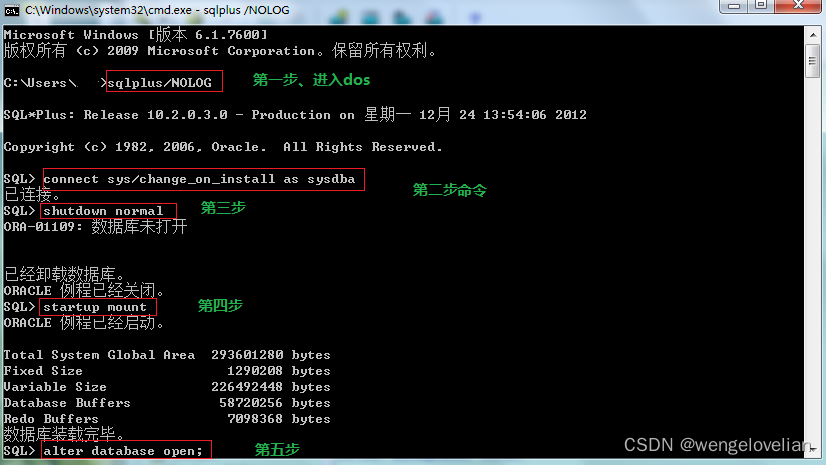
oracle 启动命令以及ORA-01033问题处理、删除归档日志
1 启动数据库:startup 2 关闭数据库:Shutdown immediate 3 查看监听状态:lsnrctl status 4 启动监听:lsnrctl start 5 停止监听:lsnrctl stop 常见问题 1、在服务器重启后会出现,Oracle ORA-01033: ORAC…...
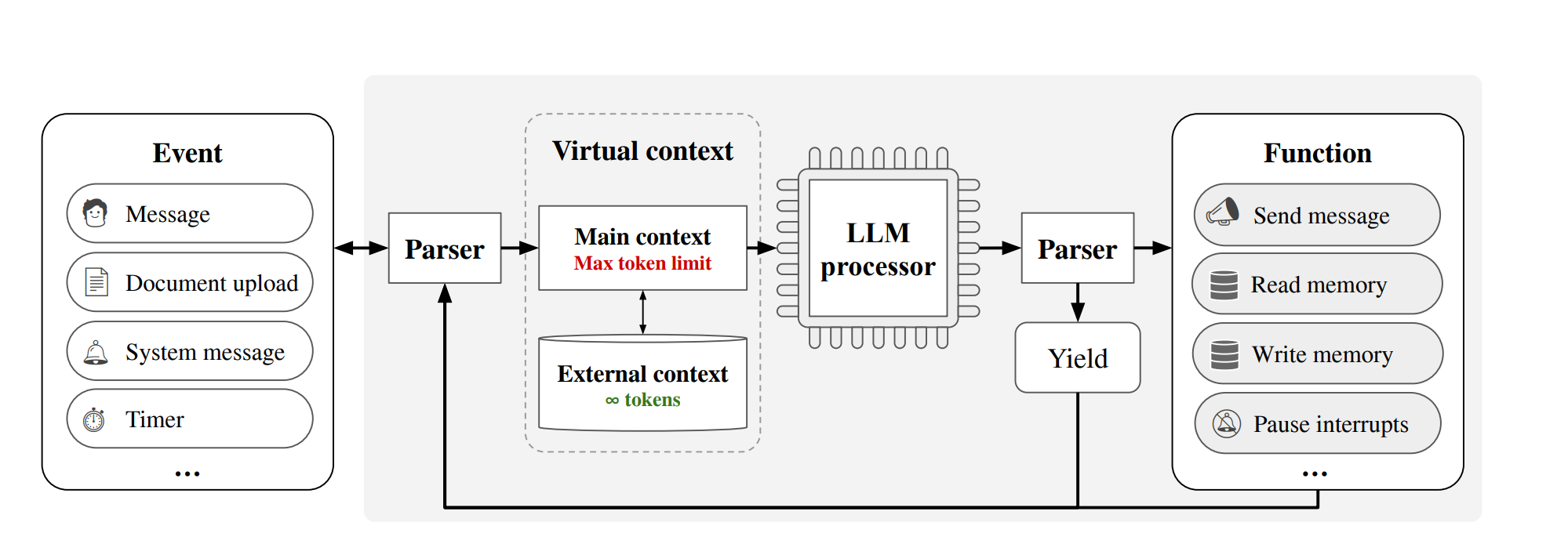
【大模型上下文长度扩展】MedGPT:解决遗忘 + 永久记忆 + 无限上下文
MedGPT:解决遗忘 永久记忆 无限上下文 问题:如何提升语言模型在长对话中的记忆和处理能力?子问题1:有限上下文窗口的限制子问题2:复杂文档处理的挑战子问题3:长期记忆的维护子问题4:即时信息检…...
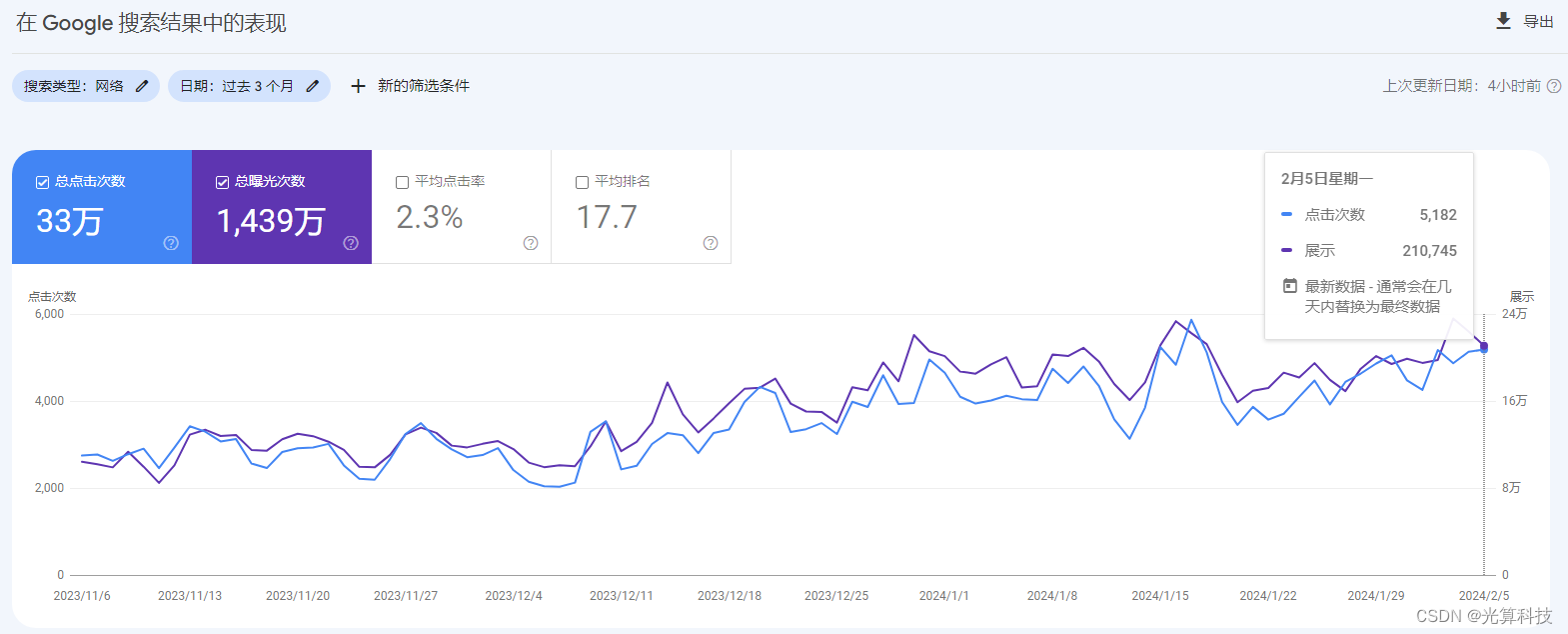
谷歌seo搜索引擎优化有什么思路?
正常做seo哪有那么多思路,其实就那么几种方法,无非就关键词,站内优化,外链,可以说万变不离其宗,但如果交给我们,你就可以实现其他的思路,或者说玩法 收录可以说是一个网站的基础&…...

腾讯云与IBM共同打造“高性能计算服务解决方案“
腾讯云与IBM共同打造"高性能计算服务解决方案" 腾讯云与IBM达成战略合作,对优势产品及服务进行深度集成,基于腾讯云产品及服务,共同打造"腾讯-IBM混合云与人工智能解决方案"。双方通过更为紧密的嵌入式解决方案的深度合…...

【SparkML实践7】特征选择器FeatureSelector
本节介绍了用于处理特征的算法,大致可以分为以下几组: 提取(Extraction):从“原始”数据中提取特征。转换(Transformation):缩放、转换或修改特征。选择(Selection&…...

LeetCode983. Minimum Cost For Tickets——动态规划
文章目录 一、题目二、题解 一、题目 You have planned some train traveling one year in advance. The days of the year in which you will travel are given as an integer array days. Each day is an integer from 1 to 365. Train tickets are sold in three differen…...
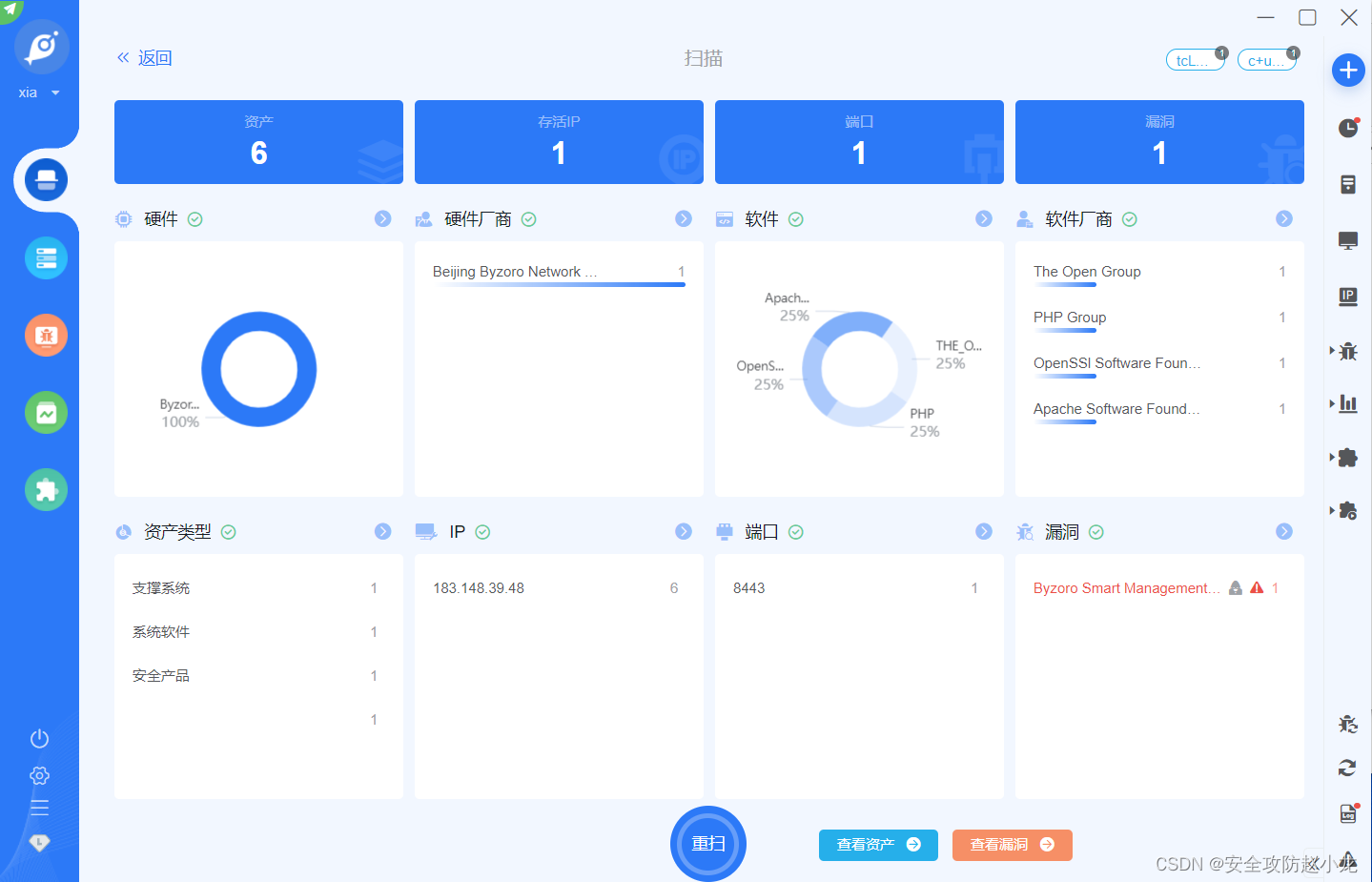
百卓Smart管理平台 uploadfile.php 文件上传漏洞【CVE-2024-0939】
百卓Smart管理平台 uploadfile.php 文件上传漏洞【CVE-2024-0939】 一、 产品简介二、 漏洞概述三、 影响范围四、 复现环境五、 漏洞复现手动复现小龙验证Goby验证 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工…...

项目中常用的一些数据库及缓存
1、常见的开发工具介绍 MySQL: MySQL是一种流行的开源关系型数据库管理系统(RDBMS),由瑞典MySQL AB公司开发,并在后来被Sun Microsystems收购,最终成为Oracle公司的一部分。MySQL广泛用于各种Web应用程序和大型企业应…...
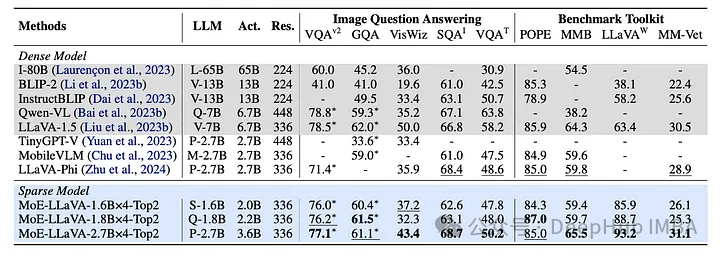
MoE-LLaVA:具有高效缩放和多模态专业知识的大型视觉语言模型
视觉和语言模型的交叉导致了人工智能的变革性进步,使应用程序能够以类似于人类感知的方式理解和解释世界。大型视觉语言模型(LVLMs)在图像识别、视觉问题回答和多模态交互方面提供了无与伦比的能力。 MoE-LLaVA利用了“专家混合”策略融合视觉和语言数据࿰…...

【Java】ArrayList和LinkedList的区别是什么
目录 1. 数据结构 2. 性能特点 3. 源码分析 4. 代码演示 5. 细节和使用场景 ArrayList 和 LinkedList 分别代表了两类不同的数据结构:动态数组和链表。它们都实现了 Java 的 List 接口,但是有着各自独特的特点和性能表现。 1. 数据结构 ArrayList…...
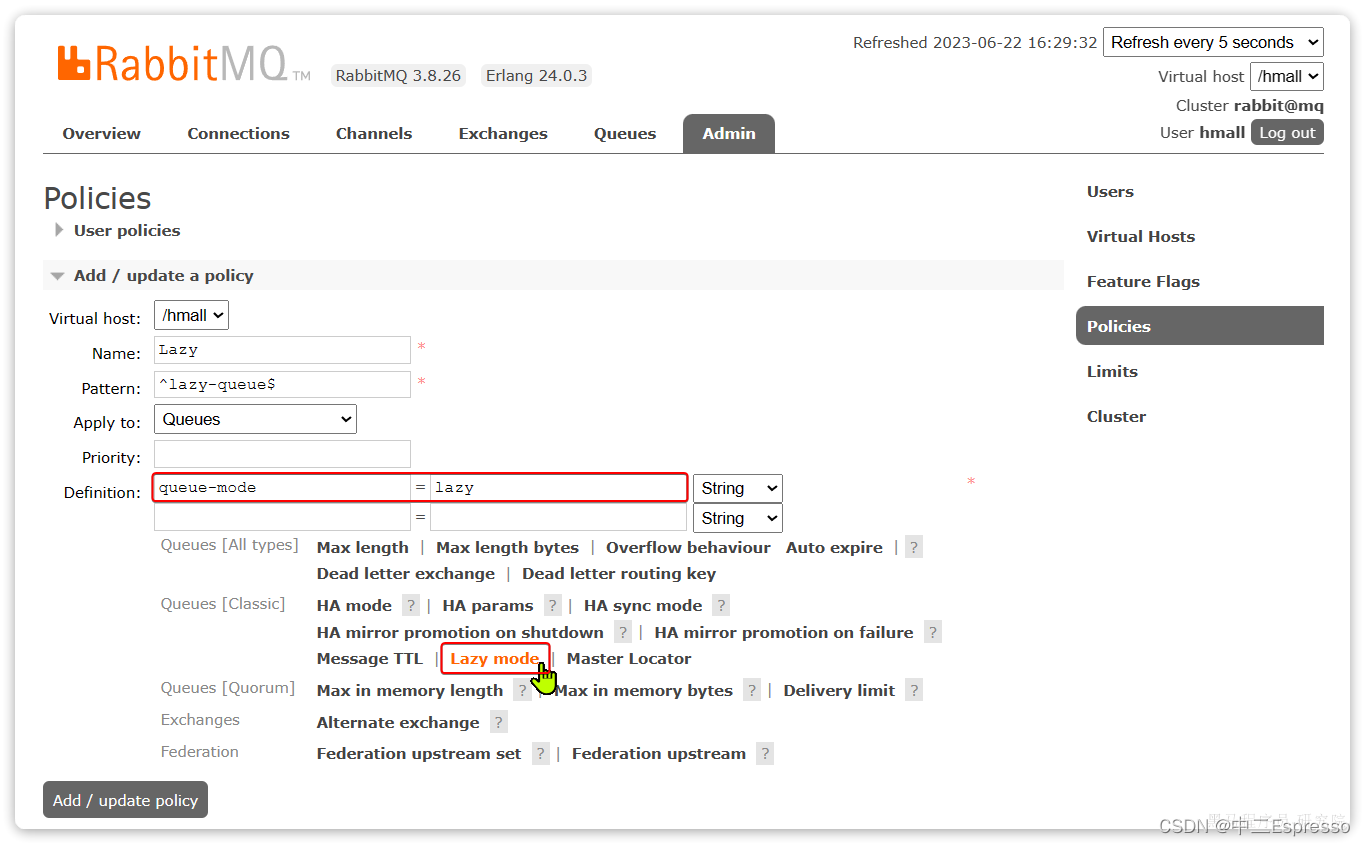
RabbitMQ-4.MQ的可靠性
MQ的可靠性 4.MQ的可靠性4.1.数据持久化4.1.1.交换机持久化4.1.2.队列持久化4.1.3.消息持久化 4.2.LazyQueue4.2.1.控制台配置Lazy模式4.2.2.代码配置Lazy模式4.2.3.更新已有队列为lazy模式 4.MQ的可靠性 消息到达MQ以后,如果MQ不能及时保存,也会导致消…...

编程相关的经典的网站和书籍
经典网站: Stack Overflow:作为全球最大的程序员问答社区,Stack Overflow 汇聚了大量的编程问题和解答,为程序员提供了极大的帮助。GitHub:全球最大的开源代码托管平台,程序员可以在上面共享自己的项目代码…...

Java代码实现基数排序算法(附带源码)
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。 1. 基数排序…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
