【机器学习笔记】贝叶斯学习
贝叶斯学习
文章目录
- 贝叶斯学习
- 1 贝叶斯学习背景
- 2 贝叶斯定理
- 3 最大后验假设MAP(Max A Posterior)
- 4 极大似然假设ML(Maximum Likelihood)
- 5 朴素贝叶斯NB
- 6 最小描述长度MDL
1 贝叶斯学习背景
试图发现两件事情的关系(因果关系,先决条件&结论)。
执果索因:肺炎→肺癌?不好确定,换成确诊肺癌得肺炎的概率
2 贝叶斯定理
贝叶斯定理是一种用先验慨率来推断后验慨率的公式,它可以表示为:
P ( h ∣ D ) = P ( D ∣ h ) P ( h ) P ( D ) P(h|D) = \frac{P(D|h)P(h)}{P(D)} P(h∣D)=P(D)P(D∣h)P(h)
-
P ( h ∣ D ) P(h|D) P(h∣D) 是后验概率,表示在已知事件 D 发生的情况下,事件 h 发生的概率;
-
P ( h ) P(h) P(h) 是 h 的先验概率,表示在没有任何其他信息的情况下,事件 h 发生的概率;
h h h 代表假设,应互相排斥;且假设空间 H H H 完全详尽,即 ∑ P ( h i ) = 1 \sum P(h_i)=1 ∑P(hi)=1
-
P ( D ) P(D) P(D) 是证据概率,表示在没有任何其他信息的情况下,事件 D 发生的概率;
D D D 代表数据的一个采样集合,需要与 h h h 独立。
-
P ( D ∣ h ) P(D|h) P(D∣h) 是似然概率,表示在已知事件 h 发生的情况下,事件 D 发生的概率;
在实践上往往取 l o g log log ,是可以得到的概率。
举例: h h h 代表得了癌症, D D D 为测试结果为阳性。
P ( h ∣ D ) P(h|D) P(h∣D):已知测试结果为阳性,得癌症的概率。
P ( D ∣ h ) P(D|h) P(D∣h):已知得了癌症,测试结果为阳性的概率。
我们已知:
- 正确的阳性样本: 98% (患有该癌症, 测试结果为 +)
- 正确的阴性样本: 97% (未患该癌症, 测试结果为 -)
- 在整个人群中,只有0.008 的人患这种癌症
如果一个人测试结果阳性,多大概率得癌症?
∵ P ( + ∣ cancer ) = 0.98 ; P ( cancer ) = 0.008 ; P ( − ∣ ¬ cancer ) = 0.97 ; ∴ P ( + ∣ ¬ cancer ) = 0.03 ; P ( ¬ cancer ) = 0.992 P ( + ) = ∑ i P ( + ∣ h i ) P ( h i ) = P ( + ∣ cancer ) P ( cancer ) + P ( + ∣ ¬ cancer ) P ( ¬ cancer ) P ( cancer ∣ + ) = P ( + ∣ cancer ) P ( cancer ) P ( + ) = 0.98 × 0.008 0.98 × 0.008 + 0.03 × 0.992 = 0.21 \because P(+|\text{cancer})=0.98;P(\text{cancer})=0.008;P(-|\neg \text{cancer})=0.97; \\\therefore P(+|\neg \text{cancer})=0.03;P(\neg \text{cancer})=0.992 \\P(+)=\sum_iP(+|h_i)P(h_i)=P(+|\text{cancer})P(\text{cancer})+P(+|\neg \text{cancer})P(\neg \text{cancer}) \\P(\text{cancer}|+)=\frac{P(+|\text{cancer})P(\text{cancer})}{P(+)}=\frac{0.98×0.008}{0.98×0.008+0.03×0.992}=0.21 ∵P(+∣cancer)=0.98;P(cancer)=0.008;P(−∣¬cancer)=0.97;∴P(+∣¬cancer)=0.03;P(¬cancer)=0.992P(+)=i∑P(+∣hi)P(hi)=P(+∣cancer)P(cancer)+P(+∣¬cancer)P(¬cancer)P(cancer∣+)=P(+)P(+∣cancer)P(cancer)=0.98×0.008+0.03×0.9920.98×0.008=0.21
3 最大后验假设MAP(Max A Posterior)
求在给定训练集上最有可能的假设。
h MAP = argmax h ∈ H P ( D ∣ h ) P ( h ) h_{\text{MAP}}=\underset{h∈H}{\text{argmax}}\ P(D|h)P(h) hMAP=h∈Hargmax P(D∣h)P(h)
argmax h ∈ H \underset{h∈H}{\text{argmax}} h∈Hargmax 指令后续公式取值最大的参数 h h h。
最大后验概率的思想是,在有一些关于参数的先验知识的情况下,根据观测数据来修正参数的概率分布,并选择使后验概率最大的参数值作为估计值。
4 极大似然假设ML(Maximum Likelihood)
如果我们完全不知道假设的概率分布,或者我们知道所有的假设发生的概率相同,那么MAP 等价于 极大似然假设 h M L h_{ML} hML (Maximum Likelihood),其公式为
h M L = arg max h i ∈ H P ( D ∣ H i ) h_{ML}=\mathop{\arg\max}_{h_i∈H}\ P(D|H_i) hML=argmaxhi∈H P(D∣Hi)
-
最小二乘LSE
最小二乘法(Least Squares Method),又称最小平方法,是一种数学优化方法,它通过最小化误差的平方和来找到数据的最佳函数匹配。假设训练数据为 < x i , d i > <x_i,d_i> <xi,di>
d i = f ( x i ) + e i d_i=f(x_i)+e_i di=f(xi)+ei
d i d_i di:独立的样本; f ( x ) f(x) f(x):没有噪声的目标函数值; e i e_i ei:噪声,独立随机变量,符合正态分布。 -
极大似然和最小二乘法的关系:
h M L = argmax h ∈ H P ( D ∣ h ) P ( h ) = argmax h ∈ H ∏ i = 1 m p ( d i ∣ h ) = argmax h ∈ H ∏ i = 1 m 1 2 π σ 2 e − 1 2 ( d i − h ( x i ) σ ) 2 (正态分布) = argmax h ∈ H ∑ i = 1 m ln 1 2 π σ 2 − 1 2 ( d i − h ( x i ) σ ) 2 (取ln,单调性) = argmax h ∈ H ∑ i = 1 m ( d i − h ( x i ) ) 2 (最小二乘) \begin{align} h_{ML} & = \underset{h∈H}{\text{argmax}}\ P(D|h)P(h) \\ & = \underset{h∈H}{\text{argmax}}\ \prod_{i=1}^mp(d_i|h) \\ & = \underset{h∈H}{\text{argmax}}\ \prod_{i=1}^m\frac{1}{\sqrt{2π\sigma^2}}e^{-\frac{1}{2}(\frac{d_i-h(x_i)}{\sigma})^2}&\text{(正态分布)} \\ & = \underset{h∈H}{\text{argmax}}\ \sum_{i=1}^m \ln\frac{1}{\sqrt{2π\sigma^2}}-\frac{1}{2}(\frac{d_i-h(x_i)}{\sigma})^2&\text{(取ln,单调性)} \\ & = \underset{h∈H}{\text{argmax}}\ \sum_{i=1}^m (d_i-h(x_i))^2&\text{(最小二乘)}\\ \end{align} hML=h∈Hargmax P(D∣h)P(h)=h∈Hargmax i=1∏mp(di∣h)=h∈Hargmax i=1∏m2πσ21e−21(σdi−h(xi))2=h∈Hargmax i=1∑mln2πσ21−21(σdi−h(xi))2=h∈Hargmax i=1∑m(di−h(xi))2(正态分布)(取ln,单调性)(最小二乘)
在独立随机变量,正态分布噪声的情况下, h M L = h L S E h_{ML}=h_{LSE} hML=hLSE
5 朴素贝叶斯NB
朴素贝叶斯的核心思想是,根据贝叶斯定理,后验概率 P(Y|X) 与先验概率 P(Y) 和似然概率 P(X|Y) 成正比
朴素贝叶斯假设:
P ( x ∣ y i ) = P ( a 1 , a 2 . . . a n ∣ v j ) = ∏ i P ( a i ∣ v j ) P(x|y_i)=P(a_1,a_2...a_n|v_j) =\prod_iP(a_i|v_j) P(x∣yi)=P(a1,a2...an∣vj)=i∏P(ai∣vj)
a 1 , a 2 . . . a n a_1,a_2...a_n a1,a2...an是相互独立的属性, v j v_j vj某条件。
朴素贝叶斯分类器:
v NB = arg max v i ∈ V { log P ( v j ) + ∑ i log P ( a i ∣ v j ) } v_{\text{NB}}=\mathop{\arg\max}_{vi∈V}\{\log P(v_j)+\sum_i\log P(a_i|v_j) \} vNB=argmaxvi∈V{logP(vj)+i∑logP(ai∣vj)}
如果满足属性之间的独立性,那么 v MAP = v NB v_{\text{MAP}}=v_{\text{NB}} vMAP=vNB
举例1:词义消歧 (Word Sense Disambiguation)
对于单词 w,使用上下文 c 进行词义消歧
e.g. "A fly flies into the kitchen while he fry the chicken. "
如何判断fly的含义?根据上下文 c c c 在词 w w w 周围一组词 w i w_i wi (特征),进行判断词义 s i s_i si
朴素贝叶斯假设: P ( c ∣ s k ) = ∏ w i ∈ c P ( w i ∣ s k ) P(c|s_k) = \prod_{w_i∈c} P(w_i|s_k) P(c∣sk)=∏wi∈cP(wi∣sk)
朴素贝叶斯选择: s = a r g m a x s k { log P ( s k ) + ∑ w i ∈ c log P ( w i ∣ s k ) } s=\underset{s_k}{argmax}\{\log P(s_k)+\sum_{w_i∈c}\log P(w_i|s_k) \} s=skargmax{logP(sk)+∑wi∈clogP(wi∣sk)}
其中 P ( s k ) = C ( s k ) C ( w ) , P ( w i ∣ s k ) = C ( w i , s k ) C ( s k ) P(s_k)=\frac{C(s_k)}{C(w)},P(w_i|s_k)=\frac{C(w_i,s_k)}{C(s_k)} P(sk)=C(w)C(sk),P(wi∣sk)=C(sk)C(wi,sk)
举例 2: 垃圾邮件过滤
经验:数据量要大;注重邮件头;不对词进行词干化;只用最显著的词;对假阳性做偏置
6 最小描述长度MDL
偏向假设 h 使得最小化
h MDL = arg min h ∈ H { L C 1 ( h ) + L C 2 ( D ∣ h ) } h_{\text{MDL}}=\mathop{\arg\min}_{h∈H}\{L_{C_1}(h)+L_{C_2}(D|h) \} hMDL=argminh∈H{LC1(h)+LC2(D∣h)}
其中 L C x L_{C_x} LCx 是 x x x 在编码 C C C 下的描述长度。
为可能性较大的消息赋予较短的编码
在对信息编码时,更偏好 一个短的且错误更少的假设,而不是一个长的但完美分类训练数据的假设
相关文章:

【机器学习笔记】贝叶斯学习
贝叶斯学习 文章目录 贝叶斯学习1 贝叶斯学习背景2 贝叶斯定理3 最大后验假设MAP(Max A Posterior)4 极大似然假设ML(Maximum Likelihood)5 朴素贝叶斯NB6 最小描述长度MDL 1 贝叶斯学习背景 试图发现两件事情的关系(因果关系,先决条件&结论&#x…...
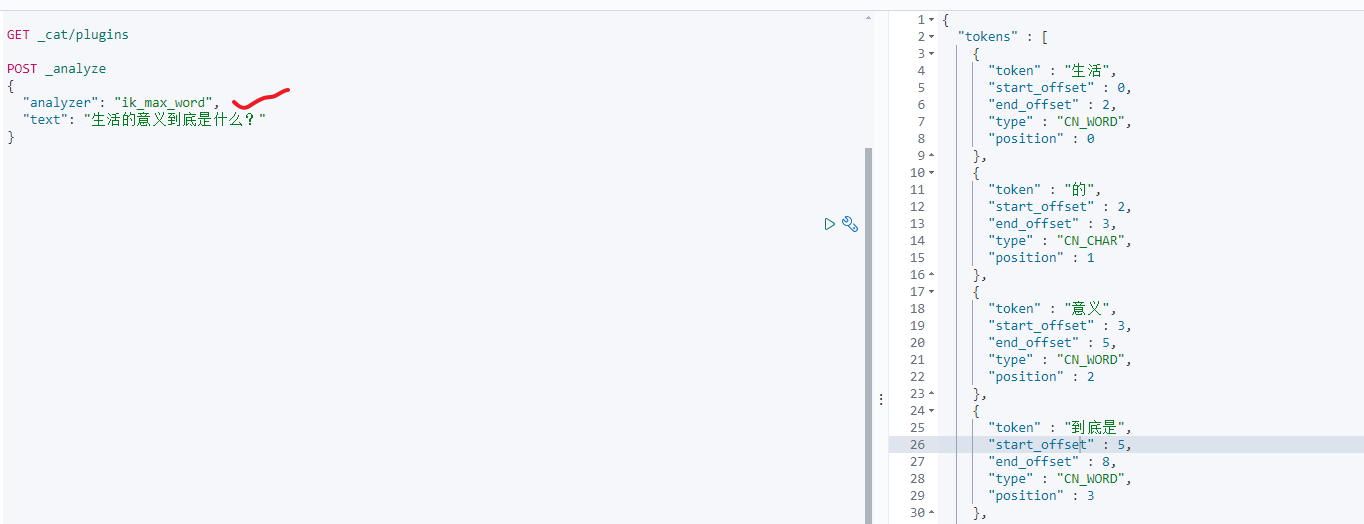
ElasticSearch之倒排索引
写在前面 本文看下es的倒排索引相关内容。 1:正排索引和倒排索引 正排索引就是通过文档id找文档内容,而倒排索引就是通过文档内容找文档id,如下图: 2:倒排索引原理 假定我们有如下的数据: 为了建立倒…...

win11安装mysql8.3.0压缩包版 240206
mysql社区版安装包版windows安装包下载地址 在系统环境变量path无点.的情况下 powershell 可以 .\ 或 ./ 开头表示当前文件夹cmd 可以直接命令或.\开头, 不能./开头 所以 .\ 在cmd和powershell中通用 步骤 在解压目录 .\mysqld --initialize-insecure root无密码初始化.\m…...

数据库索引与优化:深入了解索引的种类、使用与优化
数据库索引与优化:深入了解索引的种类、使用与优化 索引的种类 数据库索引是提高查询速度的重要手段之一,主要分为以下几种类型: 主键索引(Primary Key Index): 唯一标识表中的每一行数据,保…...

React 错误边界组件 react-error-boundary 源码解析
文章目录 捕获错误 hook创建错误边界组件 Provider定义错误边界组件定义边界组件状态捕捉错误渲染备份组件重置组件通过 useHook 控制边界组件 捕获错误 hook getDerivedStateFromError 返回值会作为组件的 state 用于展示错误时的内容 componentDidCatch 创建错误边界组件 P…...

分享66个相册特效,总有一款适合您
分享66个相册特效,总有一款适合您 66个相册特效下载链接:https://pan.baidu.com/s/1jqctaho4sL_iGSNExhWB6A?pwd8888 提取码:8888 Python采集代码下载链接:采集代码.zip - 蓝奏云 学习知识费力气,收集整理更不…...

chagpt的原理详解
GPT(Generative Pre-trained Transformer)是一种基于Transformer架构的生成式预训练模型。GPT-3是其中的第三代,由OpenAI开发。下面是GPT的基本原理: Transformer架构: GPT基于Transformer架构,该架构由Att…...

dockerfile 详细讲解
当编写 Dockerfile 时,你需要考虑你的应用程序所需的环境和依赖项,并将其描述为一系列指令。下面是一个简单的示例,演示如何编写一个用于部署基于 Node.js 的网站的 Dockerfile: Dockerfile # 使用官方 Node.js 镜像作为基础镜像…...
跟着pink老师前端入门教程-day23
苏宁网首页案例制作 设置视口标签以及引入初始化样式 <meta name"viewport" content"widthdevice-width, user-scalableno, initial-scale1.0, maximum-scale1.0, minimum-scale1.0"> <link rel"stylesheet" href"css/normaliz…...
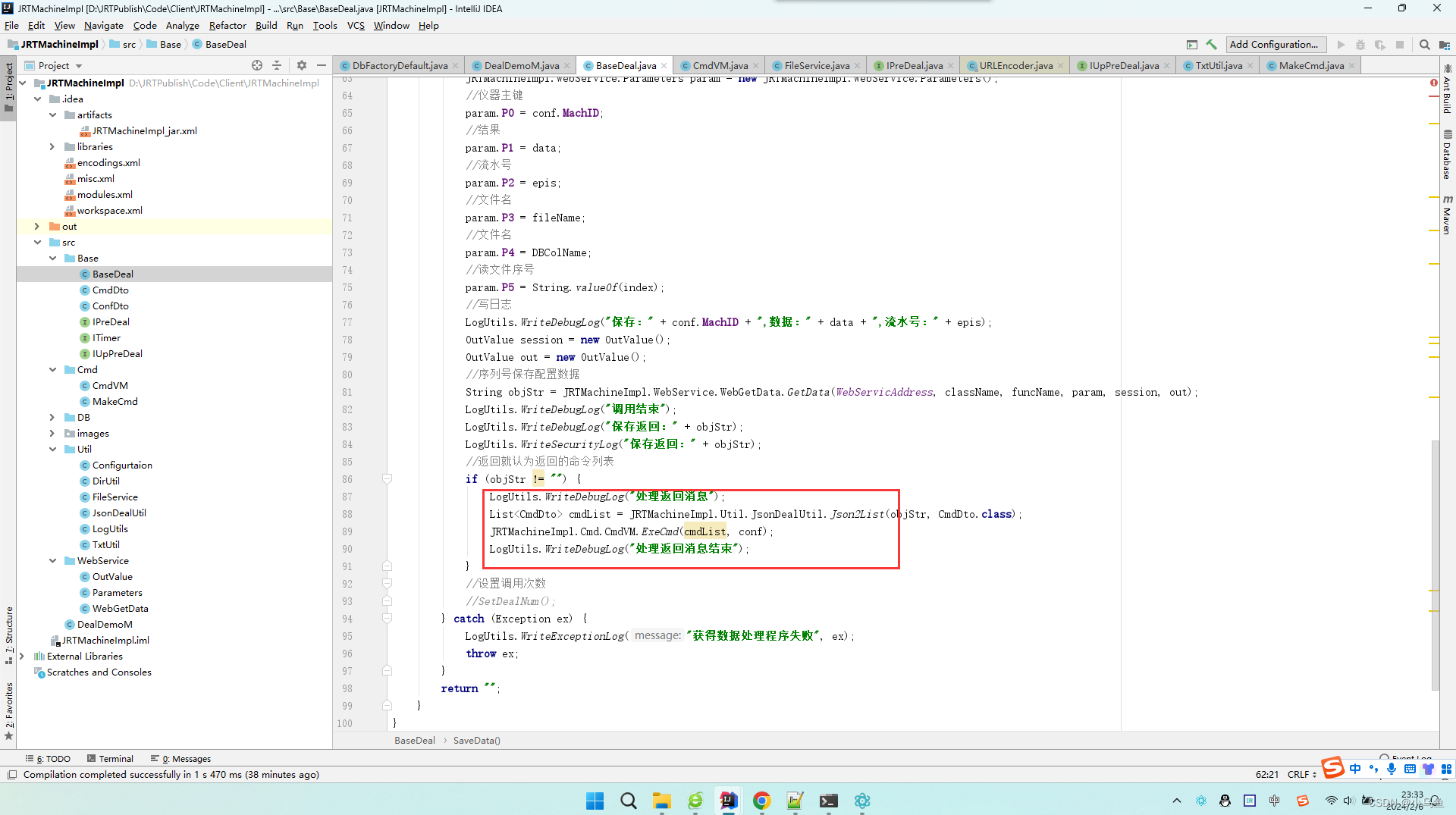
JRT监听程序
本次设计避免以往设计缺陷,老的主要为了保持兼容性,在用的设计就不好调了。 首先,接口抽象时候就不在给参数放仪器ID和处理类了,直接放仪器配置实体,接口实现想用什么属性就用什么属性,避免老方式要扩参数时…...
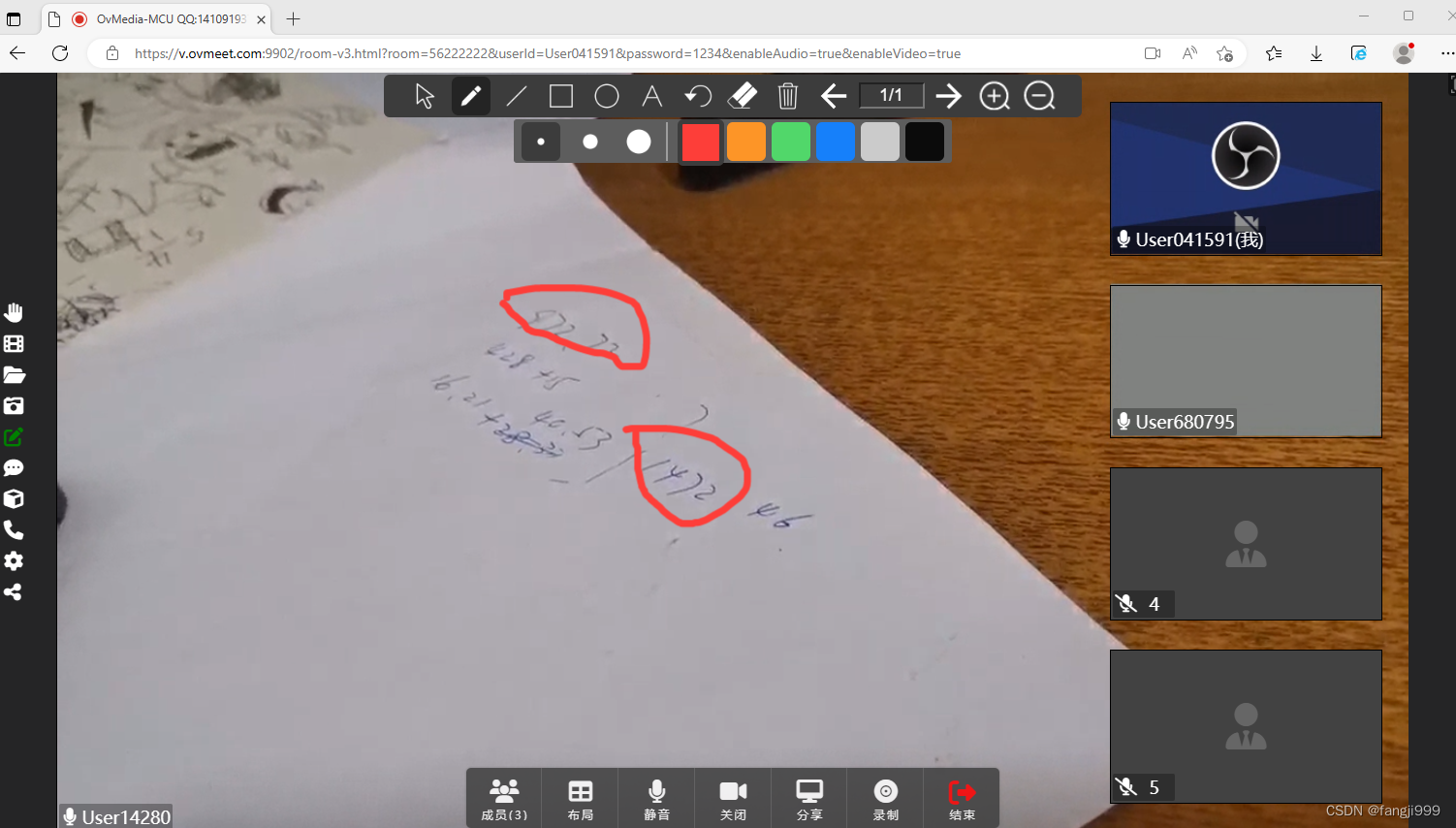
MCU+SFU视频会议一体化,视频监控,指挥调度(AR远程协助)媒体中心解决方案。
视频互动应用已经是政务和协同办公必备系统,早期的分模块,分散的视频应该不能满足业务需要,需要把视频监控,会议,录存一体把视频资源整合起来,根据客户需求,需要能够多方视频互动,直…...
)
1184. 欧拉回路(欧拉回路,模板题)
活动 - AcWing 给定一张图,请你找出欧拉回路,即在图中找一个环使得每条边都在环上出现恰好一次。 输入格式 第一行包含一个整数 t,t∈{1,2},如果 t1,表示所给图为无向图,如果 t2,表示所给图为…...

学习 Redis 基础数据结构,不讲虚的。
学习 Redis 基础数据结构,不讲虚的。 一个群友给我发消息,“该学的都学了,怎么就找不到心意的工作,太难了”。 很多在近期找过工作的同学一定都知道了,背诵八股文已经不是找工作的绝对王牌。企业最终要的是可以创造价…...

Android 11 webview webrtc无法使用问题
问题:Android 11 webview 调用webrtc无法使用, 看logcat日志会报如下错误 [ERROR:address_tracker_linux.cc(245)] Could not send NETLINK request: Permission denied (13) 查了下相关的网络权限都有配置了还是不行,还是报这个权限问题 原因࿱…...
嵌入式单片机中晶振的工作原理
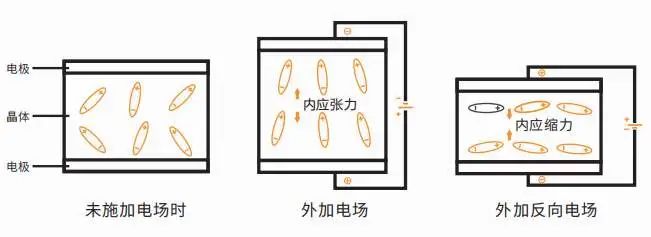
晶振在单片机中是必不可少的元器件,只要用到CPU的地方就必定有晶振的存在,那么晶振是如何工作的呢? 什么是晶振 晶振一般指晶体振荡器,晶体振荡器是指从一块石英晶体上按一定方位角切下的薄片,简称为晶片。 石英晶体谐…...
AWS配置内网EC2服务器上网【图形化配置】
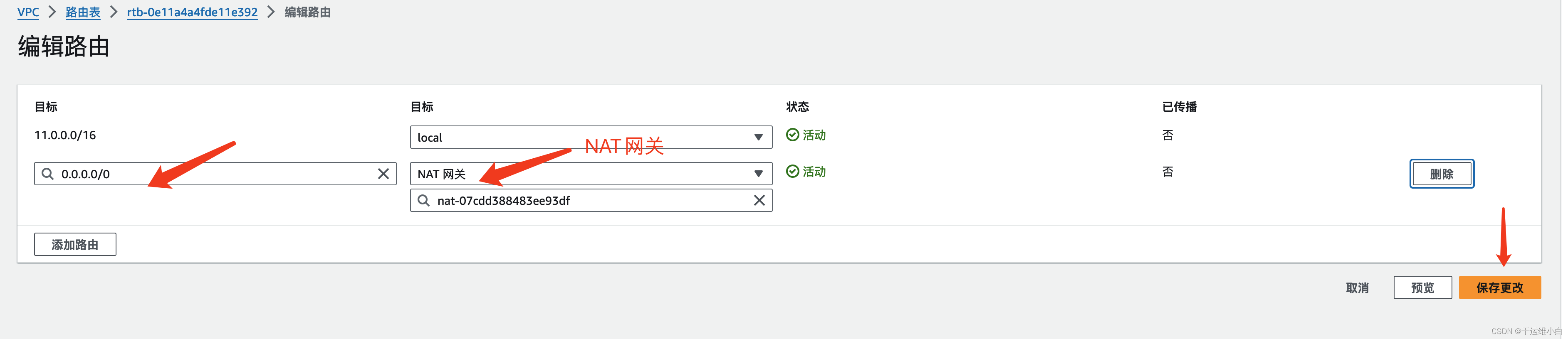
第一种方法:创建EC2选择启用分配公网ip 1. 创建vpc 2. 创建子网 3. 创建互联网网关 创建互联网网关 创建互联网网关 ,设置名称即可 然后给网关附加到新建的vpc即可 4. 给新建子网添加路由规则,添加新建的互联网网关然后点击保存更改 5. 新建…...
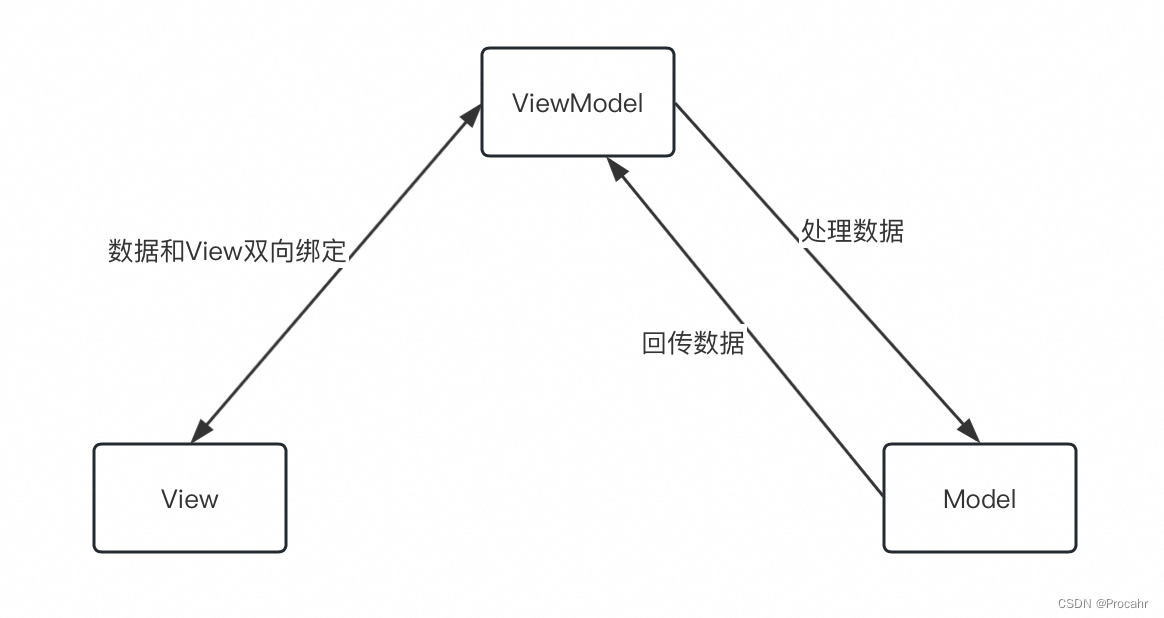
Android中的MVVM
演变 开发常用的框架包括MVC、MVP和本文的MVVM,三种框架都是为了分离ui界面和处理逻辑而出现的框架模式。mvp、mvvm都由mvc演化而来,他们不属于某种语言的框架,当存在ui页面和逻辑代码时,我们就可以使用这三种模式。 model和vie…...

制作耳机壳的UV树脂和塑料材质相比劣势有哪些?
以下是UV树脂相比塑料材质可能存在的劣势: 价格较高:相比一些常见的塑料材质,UV树脂的价格可能较高。这主要是因为UV树脂的生产过程较为复杂,需要较高的技术和设备支持。加工难度大:虽然UV树脂的加工过程相对简单&…...

CSP-202012-1-期末预测之安全指数
CSP-202012-1-期末预测之安全指数 题目很简单,直接上代码 #include <iostream> using namespace std; int main() {int n, sum 0;cin >> n;for (int i 0; i < n; i){int w, score;cin >> w >> score;sum w * score;}if (sum > 0…...

Doris中的本地routineload环境,用于开发回归测试用例
----------------2024-2-6-更新-------------- doris的routineload,就是从kafka中加载数据到表,特点是定时、周期性的从kafka取数据。 要想在本地开发测试routine load相关功能,需要配置kafka环境,尤其是需要增加routine load回…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...
