《动手学深度学习(PyTorch版)》笔记8.3
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过,同时对于书上部分章节也做了整合。
Chapter8 Recurrent Neural Networks
8.3 Language Models and the Dataset
假设长度为 T T T的文本序列中的词元依次为 x 1 , x 2 , … , x T x_1, x_2, \ldots, x_T x1,x2,…,xT。于是, x t x_t xt( 1 ≤ t ≤ T 1 \leq t \leq T 1≤t≤T)可以被认为是文本序列在时间步 t t t处的观测或标签。在给定这样的文本序列时,语言模型(language model)的目标是估计序列的联合概率 P ( x 1 , x 2 , … , x T ) . P(x_1, x_2, \ldots, x_T). P(x1,x2,…,xT).例如,只需要一次抽取一个词元 x t ∼ P ( x t ∣ x t − 1 , … , x 1 ) x_t \sim P(x_t \mid x_{t-1}, \ldots, x_1) xt∼P(xt∣xt−1,…,x1),一个理想的语言模型就能够基于模型本身生成自然文本。
8.3.1 Learning a Language Model
假设在单词级别对文本数据进行词元化,包含了四个单词的一个文本序列的概率是:
P ( deep , learning , is , fun ) = P ( deep ) P ( learning ∣ deep ) P ( is ∣ deep , learning ) P ( fun ∣ deep , learning , is ) . P(\text{deep}, \text{learning}, \text{is}, \text{fun}) = P(\text{deep}) P(\text{learning} \mid \text{deep}) P(\text{is} \mid \text{deep}, \text{learning}) P(\text{fun} \mid \text{deep}, \text{learning}, \text{is}). P(deep,learning,is,fun)=P(deep)P(learning∣deep)P(is∣deep,learning)P(fun∣deep,learning,is).
为了训练语言模型,我们需要计算单词的概率,以及给定前面几个单词后出现某个单词的条件概率,这些概率本质上就是语言模型的参数。假设训练集是一个大型的文本语料库,训练集中词的概率可以根据给定词的相对词频来计算,比如可以将估计值 P ^ ( deep ) \hat{P}(\text{deep}) P^(deep)计算为任何以单词“deep”开头的句子的概率。一种(稍稍不太精确的)方法是统计单词“deep”在数据集中的出现次数,然后将其除以整个语料库中的单词总数(不太精确指的是:单个词的出现概率可能会受到其周围上下文的影响;“稀有词”可能会导致参数估计不准确,因为在训练集中可能无法捕获到这些词在其他文本中的真实分布情况;某个词在语料库中出现的次数可能会受到文本主题、文体等因素的影响)。接下来,我们可以尝试估计
P ^ ( learning ∣ deep ) = n ( deep, learning ) n ( deep ) , \hat{P}(\text{learning} \mid \text{deep}) = \frac{n(\text{deep, learning})}{n(\text{deep})}, P^(learning∣deep)=n(deep)n(deep, learning),
其中 n ( x ) n(x) n(x)和 n ( x , x ′ ) n(x, x') n(x,x′)分别是单个单词和连续单词对的出现次数。不幸的是,由于连续单词对“deep learning”的出现频率要低得多,所以估计这类单词正确的概率要困难得多。除非我们提供某种解决方案,来将这些单词组合指定为非零计数,否则将无法在语言模型中使用它们。一种常见的策略是执行某种形式的拉普拉斯平滑(Laplace smoothing),具体方法是在所有计数中添加一个小常量。用 n n n表示训练集中的单词总数,用 m m m表示唯一单词的数量,如下式所示:
P ^ ( x ) = n ( x ) + ϵ 1 / m n + ϵ 1 , P ^ ( x ′ ∣ x ) = n ( x , x ′ ) + ϵ 2 P ^ ( x ′ ) n ( x ) + ϵ 2 , P ^ ( x ′ ′ ∣ x , x ′ ) = n ( x , x ′ , x ′ ′ ) + ϵ 3 P ^ ( x ′ ′ ) n ( x , x ′ ) + ϵ 3 . \begin{aligned} \hat{P}(x) & = \frac{n(x) + \epsilon_1/m}{n + \epsilon_1}, \\ \hat{P}(x' \mid x) & = \frac{n(x, x') + \epsilon_2 \hat{P}(x')}{n(x) + \epsilon_2}, \\ \hat{P}(x'' \mid x,x') & = \frac{n(x, x',x'') + \epsilon_3 \hat{P}(x'')}{n(x, x') + \epsilon_3}. \end{aligned} P^(x)P^(x′∣x)P^(x′′∣x,x′)=n+ϵ1n(x)+ϵ1/m,=n(x)+ϵ2n(x,x′)+ϵ2P^(x′),=n(x,x′)+ϵ3n(x,x′,x′′)+ϵ3P^(x′′).
其中, ϵ 1 、 e p s i l o n 2 \epsilon_1、epsilon_2 ϵ1、epsilon2和 ϵ 3 \epsilon_3 ϵ3是超参数。以 ϵ 1 \epsilon_1 ϵ1为例:当 ϵ 1 = 0 \epsilon_1 = 0 ϵ1=0时,不应用平滑;当 ϵ 1 \epsilon_1 ϵ1接近正无穷大时, P ^ ( x ) \hat{P}(x) P^(x)接近均匀概率分布 1 / m 1/m 1/m。
然而,这样的模型很容易变得无效,原因如下:首先,我们需要存储所有的计数;其次,模型完全忽略了单词的意思;最后,长单词序列大部分是没出现过的,因此一个模型如果只是简单地统计先前“看到”的单词序列频率,面对这种问题时肯定表现不佳。
如果 P ( x t + 1 ∣ x t , … , x 1 ) = P ( x t + 1 ∣ x t ) P(x_{t+1} \mid x_t, \ldots, x_1) = P(x_{t+1} \mid x_t) P(xt+1∣xt,…,x1)=P(xt+1∣xt),则序列上的分布满足一阶马尔可夫性质。阶数越高,对应的依赖关系就越长。这种性质推导出了许多可以应用于序列建模的近似公式:
P ( x 1 , x 2 , x 3 , x 4 ) = P ( x 1 ) P ( x 2 ) P ( x 3 ) P ( x 4 ) P ( x 1 , x 2 , x 3 , x 4 ) = P ( x 1 ) P ( x 2 ∣ x 1 ) P ( x 3 ∣ x 2 ) P ( x 4 ∣ x 3 ) P ( x 1 , x 2 , x 3 , x 4 ) = P ( x 1 ) P ( x 2 ∣ x 1 ) P ( x 3 ∣ x 1 , x 2 ) P ( x 4 ∣ x 2 , x 3 ) \begin{aligned} P(x_1, x_2, x_3, x_4) &= P(x_1) P(x_2) P(x_3) P(x_4)\\ P(x_1, x_2, x_3, x_4) &= P(x_1) P(x_2 \mid x_1) P(x_3 \mid x_2) P(x_4 \mid x_3) \\ P(x_1, x_2, x_3, x_4) &= P(x_1) P(x_2 \mid x_1) P(x_3 \mid x_1, x_2) P(x_4 \mid x_2, x_3) \end{aligned} P(x1,x2,x3,x4)P(x1,x2,x3,x4)P(x1,x2,x3,x4)=P(x1)P(x2)P(x3)P(x4)=P(x1)P(x2∣x1)P(x3∣x2)P(x4∣x3)=P(x1)P(x2∣x1)P(x3∣x1,x2)P(x4∣x2,x3)
通常,涉及一个、两个和三个变量的概率公式分别被称为一元语法(unigram)、二元语法(bigram)和三元语法(trigram)模型。也就是说,一元语法假设文本中的每个词都是相互独立的,即某个词的出现概率只依赖不依赖于其他词,一元语法模型将整个文本的概率表示为每个单词出现的概率的乘积。二元语法考虑了相邻两个词之间的关系,假设某个词的出现概率仅依赖于它前面一个词,三元语法同理。
8.3.2 Natural Language SStatistics
import random
import torch
from d2l import torch as d2l
import matplotlib.pyplot as plttokens = d2l.tokenize(d2l.read_time_machine())
# 因为每个文本行不一定是一个句子或一个段落,因此我们把所有文本行拼接到一起
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
print(vocab.token_freqs[:10])freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',xscale='log', yscale='log')
plt.show()
词频图:

最流行的词看起来很无聊,被称为停用词(stop words),因此可以被过滤掉,但它们本身仍然是有意义的。此外,还有个明显的现象是词频衰减的速度相当快。通过此图我们可以发现:词频以一种明确的方式迅速衰减。将前几个单词作为例外消除后,剩余的所有单词大致遵循双对数坐标图(xscale=‘log’, yscale=‘log’)上的一条直线,这意味着单词的频率满足齐普夫定律(Zipf’s law),即第 i i i个最常用单词的频率 n i n_i ni满足:
log n i = − α log i + c \log n_i = -\alpha \log i + c logni=−αlogi+c
其中 α \alpha α是刻画分布的指数, c c c是常数。上式等价于
n i ∝ 1 i α n_i \propto \frac{1}{i^\alpha} ni∝iα1
这告诉我们想要通过计数统计和平滑来建模单词是不可行的,因为这样建模的结果会大大高估尾部单词的频率,也就是所谓的不常用单词。换句话说,齐普夫定律告诉我们,自然语言中的单词分布呈现出一种“长尾”现象,即少数单词的出现频率非常高,而大多数单词的出现频率则相对较低,呈现出尾部单词的大量分布。
#bigram
bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
print(bigram_vocab.token_freqs[:10])#trigram
trigram_tokens = [triple for triple in zip(corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
print(trigram_vocab.token_freqs[:10])bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',ylabel='frequency: n(x)', xscale='log', yscale='log',legend=['unigram', 'bigram', 'trigram'])
plt.show()
一元、二元和三元词频图:

从上图可看出:
- 除了一元语法词,单词序列也遵循齐普夫定律,尽管公式指数 α \alpha α更小;
- 词表中 n n n元组的数量并没有那么大,这说明语言中存在相当多的结构(即词元序列组合很丰富);
- 很多 n n n元组很少出现,这使得拉普拉斯平滑非常不适合语言建模,因此我们将使用基于深度学习的模型。
8.3.3 Reading Long Sequence Data
当序列变得太长而不能被模型一次性全部处理时,我们可能希望拆分这样的序列方便模型读取。假设我们将使用神经网络来训练语言模型,模型中的网络一次处理具有预定义长度(例如 n n n个时间步)的一个小批量序列。首先,由于文本序列可以是任意长的,于是任意长的序列可以被我们划分为具有相同时间步数的子序列。当训练我们的神经网络时,这样的小批量子序列将被输入到模型中。假设网络一次只处理具有 n n n个时间步的子序列。下图画出了从原始文本序列获得子序列的所有不同的方式,其中 n = 5 n=5 n=5,并且每个时间步的词元对应于一个字符。

事实上,上图中不同的取法都一样好,然而如果只选择一个偏移量,那么用于训练网络的、所有可能的子序列的覆盖范围将是有限的。因此,我们可以从随机偏移量开始划分序列,以同时获得覆盖性(coverage)和随机性(randomness)。
def seq_data_iter_random(corpus, batch_size, num_steps): #@save"""使用随机抽样生成一个小批量子序列"""#从随机偏移量开始对序列进行分区,随机范围为[0,num_steps-1]corpus = corpus[random.randint(0, num_steps - 1):]num_subseqs = (len(corpus) - 1) // num_steps #将输入序列中的每个词作为训练数据的特征,而将对应的下一个词作为标签,减去1是为了确保每个子序列都有对应的标签#initial_indices为长度为num_steps的子序列的起始索引initial_indices = list(range(0, num_subseqs * num_steps, num_steps))#打乱处理后,在随机抽样的迭代过程中,来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻random.shuffle(initial_indices)def data(pos):#返回从pos位置开始的长度为num_steps的序列return corpus[pos: pos + num_steps]num_batches = num_subseqs // batch_size#batch_size指定每个小批量中子序列样本的数目for i in range(0, batch_size * num_batches, batch_size):initial_indices_per_batch = initial_indices[i: i + batch_size]#initial_indices包含子序列的随机起始索引#X是模型的输入序列,Y是对应于X中每个样本的下一个词的目标序列(标签)X = [data(j) for j in initial_indices_per_batch]Y = [data(j + 1) for j in initial_indices_per_batch]yield torch.tensor(X), torch.tensor(Y)my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):print('X: ', X, '\nY:', Y)def seq_data_iter_sequential(corpus, batch_size, num_steps):#@save"""使用顺序分区生成一个小批量子序列"""# 从随机偏移量开始划分序列offset = random.randint(0, num_steps)num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_sizeXs = torch.tensor(corpus[offset: offset + num_tokens])Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])print(Xs,Ys)Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)print(Xs,Ys)num_batches = Xs.shape[1] // num_stepsfor i in range(0, num_steps * num_batches, num_steps):X = Xs[:, i: i + num_steps]Y = Ys[:, i: i + num_steps]yield X, Yfor X, Y in seq_data_iter_sequential(my_seq, batch_size=2, num_steps=5):print('X: ', X, '\nY:', Y)class SeqDataLoader: #@save"""加载序列数据的迭代器"""def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):if use_random_iter:self.data_iter_fn = d2l.seq_data_iter_randomelse:self.data_iter_fn = d2l.seq_data_iter_sequentialself.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)self.batch_size, self.num_steps = batch_size, num_stepsdef __iter__(self):return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)def load_data_time_machine(batch_size, num_steps, #@saveuse_random_iter=False, max_tokens=10000):"""返回时光机器数据集的迭代器和词表"""data_iter = SeqDataLoader(batch_size, num_steps, use_random_iter, max_tokens)return data_iter, data_iter.vocab
相关文章:

《动手学深度学习(PyTorch版)》笔记8.3
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过&…...
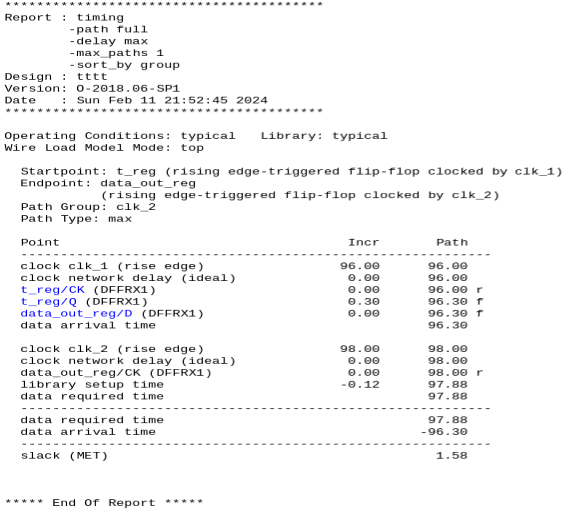
静态时序分析:建立时间分析
静态时序分析https://blog.csdn.net/weixin_45791458/category_12567571.html?spm1001.2014.3001.5482 在静态时序分析中,建立时间检查约束了触发器时钟引脚(时钟路径)和输入数据引脚(数据路径)之间的时序关系&#x…...

深入探究 HTTP 简化:httplib 库介绍
✏️心若有所向往,何惧道阻且长 文章目录 简介特性主要类介绍httplib::Server类httplib::Client类httplib::Request类httplib::Response类 示例服务器客户端 总结 简介 在当今的软件开发中,与网络通信相关的任务变得日益普遍。HTTP(Hypertext…...
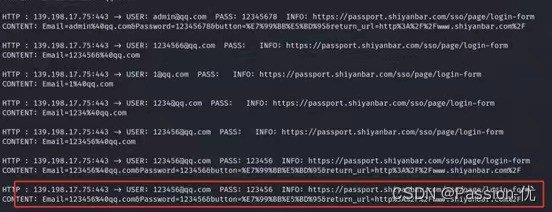
ARP欺骗攻击利用之抓取https协议的用户名与密码
1.首先安装sslstrip 命令执行:apt-get install sslstrip 2.启动arp欺骗 arpspoof -i ech0 -t 192.168.159.148 192.168.159.2 arpspoof -i ech0(网卡) -t 目标机ip 本地局域网关 3.命令行输入: vim /etc/ettercap/etter.conf进入配置文件 找到下红框的内容&a…...

<s-table>、<a-table>接收后端数据
对于 中的 <template #bodyCell“{ column, record }”> : <s-tableref"table":columns"columns":data"loadData":alert"options.alert.show"bordered:row-key"(record) > record.id":tool-config&…...

[数学]高斯消元
介绍 用处:求解线性方程组 加减消元法和代入消元法 这里引用了高斯消元解线性方程组----C实现_c用高斯消元法解线性方程组-CSDN博客 改成了自己常用的形式: int gauss() {int c, r; // column, rowfor (c 1, r 1; c < n; c ){int maxx r; //…...
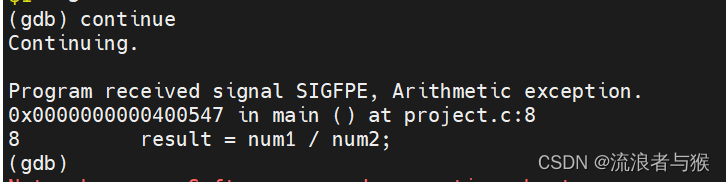
【Linux】gdb调试与make/makefile工具
目录 导读 1. make/Makefile 1.1 引入 1.2 概念 1.3 语法规则 1.4 示例 2. Linux调试器-gdb 2.1 引入 2.2 概念 2.3 使用 导读 我们在上次讲了Linux编辑器gcc\g的使用,今天我们就来进一步的学习如何调试,以及makefile这个强大的工具。 1. mak…...
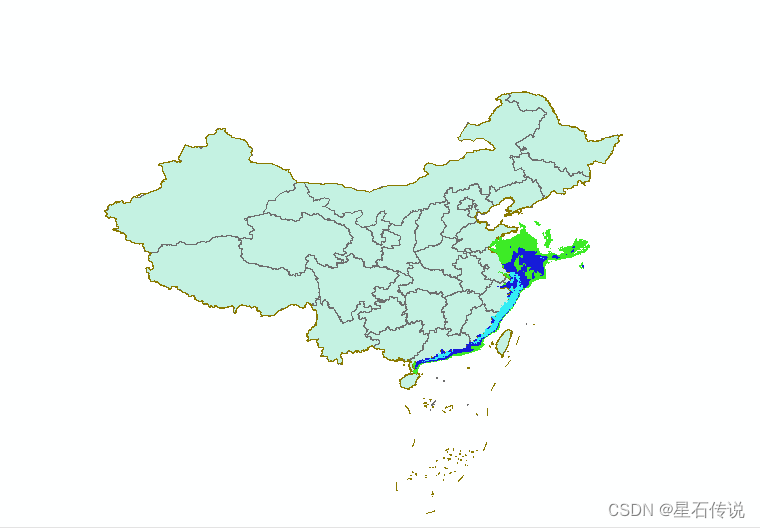
使用Arcgis裁剪
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、掩膜提取二、随意裁剪三、裁剪 前言 因为从网站下载的是全球气候数据,而我们需要截取成中国部分,需要用到Arcgis的裁剪工具 一、掩…...

sheng的学习笔记-网络爬虫scrapy框架
基础知识: scrapy介绍 何为框架,就相当于一个封装了很多功能的结构体,它帮我们把主要的结构给搭建好了,我们只需往骨架里添加内容就行。scrapy框架是一个为了爬取网站数据,提取数据的框架,我们熟知爬虫总…...

Qt PCL学习(三):点云滤波
注意事项 版本一览:Qt 5.15.2 PCL 1.12.1 VTK 9.1.0前置内容:Qt PCL学习(一):环境搭建、Qt PCL学习(二):点云读取与保存、PCL学习六:Filtering-滤波 0. 效果演示 1. vo…...

Ainx-V0.2-简单的连接封装与业务绑定
📕作者简介: 过去日记,致力于Java、GoLang,Rust等多种编程语言,热爱技术,喜欢游戏的博主。 📗本文收录于Ainx系列,大家有兴趣的可以看一看 📘相关专栏Rust初阶教程、go语言基础系列…...

《杨绛传:生活不易,保持优雅》读书摘录
目录 书简介 作者成就 书中内容摘录 良好的家世背景,书香门第为求学打基础 求学相关 念大学 清华研究生 自费英国留学 法国留学自学文学 战乱时期回国 当校长 当小学老师 创造话剧 支持钱锺书写《围城》 出任震旦女子文理学院的教授 接受清华大学的…...

ChatGPT在肾脏病学领域的专业准确性评估
ChatGPT在肾脏病学领域的专业表现评估 随着人工智能技术的飞速发展,ChatGPT作为一个先进的机器学习模型,在多个领域显示出了其对话和信息处理能力的潜力。近期发表在《美国肾脏病学会临床杂志》(影响因子:9.8)上的一项…...

Centos7.9安装SQLserver2017数据库
Centos7.9安装SQLserver2017数据库 一、安装前准备 挂载系统盘 安装依赖 yum install libatomic* -y 二、yum方式安装 # 配置 yum 源 wget -O /etc/yum.repos.d/mssql-server.repo https://packages.microsoft.com/config/rhel/7/mssql-server-2017.repoyum clean all yum…...
spring boot和spring cloud项目中配置文件application和bootstrap中的值与对应的配置类绑定处理
在前面的文章基础上 https://blog.csdn.net/zlpzlpzyd/article/details/136065211 加载完文件转换为 Environment 中对应的值之后,接下来需要将对应的值与对应的配置类进行绑定,方便对应的组件取值处理接下来的操作。 对应的配置值与配置类绑定通过 Con…...
)
每天一个数据分析题(一百五十四)
给定下面的Python代码片段,哪个选项正确描述了代码可能存在的问题? from scipy import stats 返回异常值的索引 z stats.zscore(data_raw[‘Age’]) z_outlier (z > 3) | (z < -3) z_outlier.tolist().index(1) A. 代码将返回数据集Age列中第…...

Django从入门到放弃
Django从入门到放弃 Django最初被设计用于具有快速开发需求的新闻类站点,目的是实现简单快捷的网站开发。 安装Django 使用anaconda创建环境 conda create -n django_env python3.10 conda activate django_env使用pip安装django python -m pip install Django查…...
C++中类的6个默认成员函数【构造函数】 【析构函数】
文章目录 前言构造函数构造函数的概念构造函数的特性 析构函数 前言 在学习C我们必须要掌握的6个默认成员函数,接下来本文讲解2个默认成员函数 构造函数 如果一个类中什么成员都没有,简称为空类。 空类中真的什么都没有吗?并不是,…...
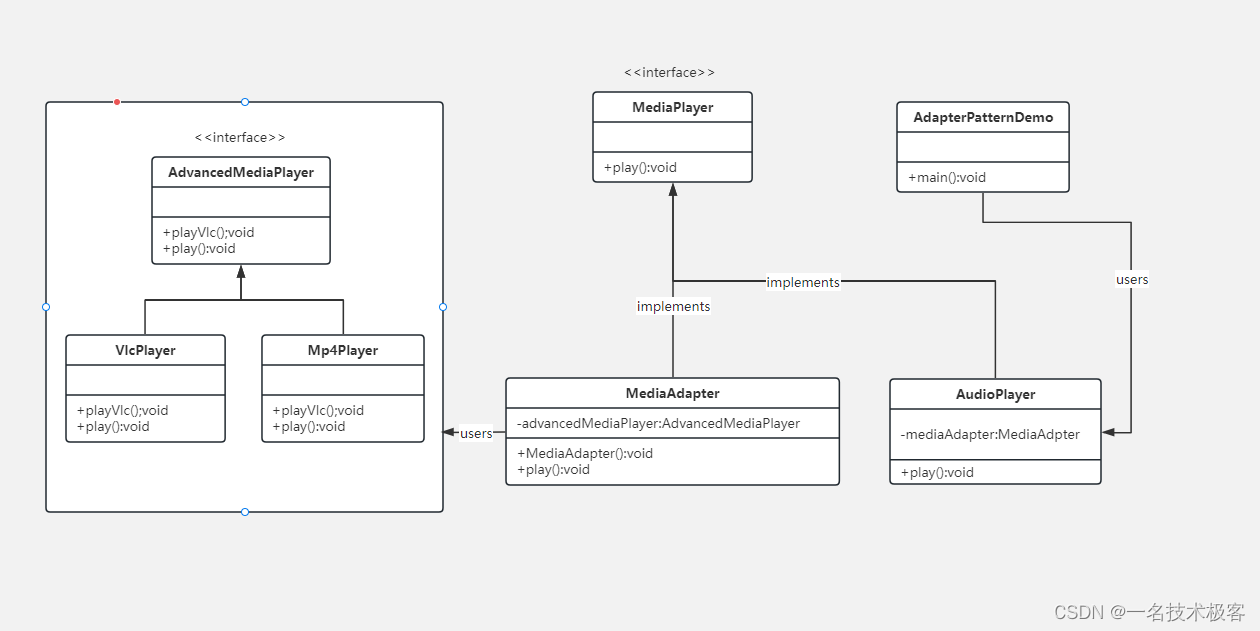
06-Java适配器模式 ( Adapter Pattern )
原型模式 摘要实现范例 适配器模式(Adapter Pattern)是作为两个不兼容的接口之间的桥梁 适配器模式涉及到一个单一的类,该类负责加入独立的或不兼容的接口功能 举个真实的例子,读卡器是作为内存卡和笔记本之间的适配器。您将内…...
C# CAD交互界面-自定义面板集-添加快捷命令(五)
运行环境 vs2022 c# cad2016 调试成功 一、引用 using Autodesk.AutoCAD.ApplicationServices; using Autodesk.AutoCAD.Runtime; using Autodesk.AutoCAD.Windows; using System; using System.Drawing; using System.Windows.Forms; 二、代码说明 [CommandMethod("Cre…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
