杨辉三角的变形(数学)
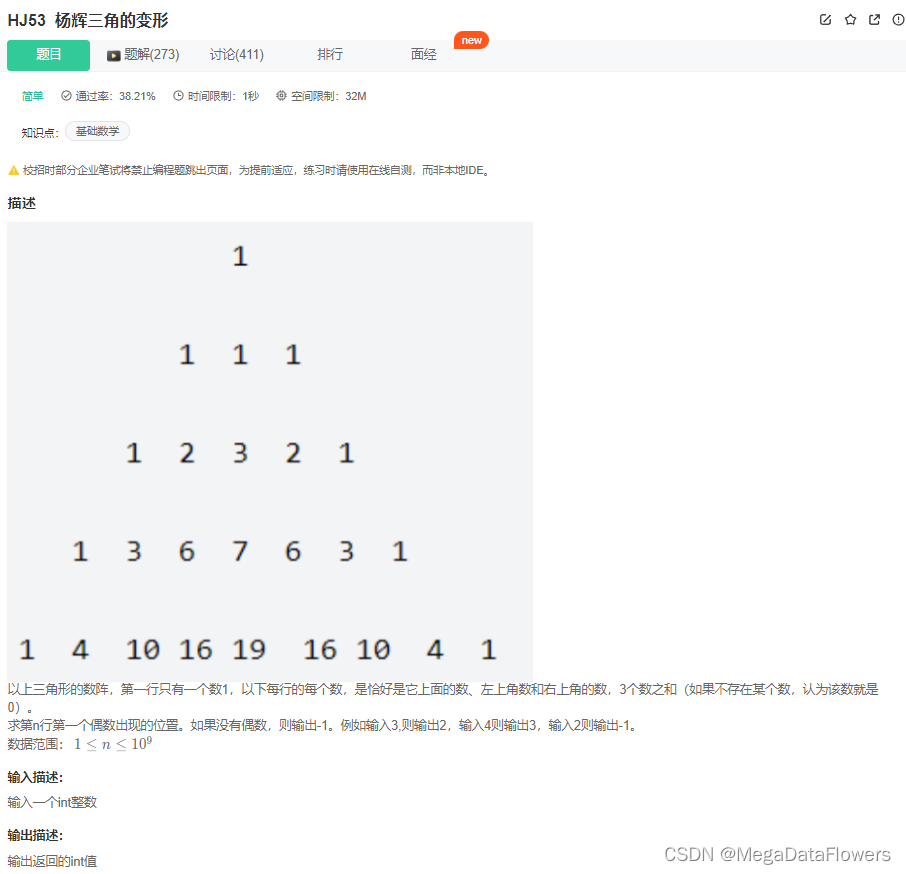
题目

import java.util.Scanner;public class Main {public static void main(String[] args) {
// 1
// 1 1 1
// 1 2 3 2 1
// 1 3 6 7 6 3 1
// 1 4 10 16 19 16 10 4 1Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[][] res = new int[n+1][2*n];for(int i=1;i<=n;i++) {res[i][1] = 1;res[i][2*i-1] = 1;}//第二列for(int i=2;i<=n;i++) {res[i][2] = res[i-1][1]+res[i-1][2];}//大于等于第三列for(int i=3;i<=n;i++) {for(int j=3;j<=(2*n-1);j++) {res[i][j] = res[i-1][j-2]+res[i-1][j-1]+res[i-1][j];}}for(int j=1;j<=(2*n-1);j++) {if(res[n][j]%2 == 0) {System.out.println(j);return ;}}System.out.println(-1);sc.close();}
}

import java.util.Scanner;public class Main {public static void main(String[] args) {
// 1
// 1 1 1
// 1 2 3 2 1
// 1 3 6 7 6 3 1
// 1 4 10 16 19 16 10 4 1Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[][] res = new int[n][2 * (n - 1) + 1];res[0][0] = 1;for (int i = 1; i < n; i++) {res[i][0] = 1;res[i][2 * i] = 1;}//第二列for (int i = 1; i < n; i++) {res[i][1] = res[i - 1][0] + res[i - 1][1];}//大于等于第三列for (int i = 2; i < n; i++) {for (int j = 2; j < 2 * (n - 1) + 1; j++) {res[i][j] = res[i - 1][j - 2] + res[i - 1][j - 1] + res[i - 1][j];}}for (int j = 0; j < 2 * (n - 1) + 1; j++) {if (res[n - 1][j] % 2 == 0) {System.out.println(j + 1);return ;}}System.out.println(-1);
// for(int i=0;i<n;i++) {
// for(int j=0;j<(2*(n-1)+1);j++){
// System.out.print(res[i][j]);
// }
// System.out.println();
// }sc.close();}
}
下标为0或者1都不能通过全部样例


import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);int num = in.nextInt();if(num == 1 || num == 2){System.out.println(-1);}else if(num % 4 == 1 || num % 4 == 3){System.out.println(2);}else if(num % 4 == 0){System.out.println(3);}else if(num % 4 == 2){System.out.println(4);}}
}
相关文章:

杨辉三角的变形(数学)
题目 import java.util.Scanner;public class Main {public static void main(String[] args) { // 1 // 1 1 1 // 1 2 3 2 1 // 1 3 6 7 6 3 1 // 1 4 10 16 19 16 10 4 1Scanner sc new Scanner(System.in);int n sc.nextInt();int[][] res new int[n1][2*n];for(i…...

YOLOv5改进 | 融合改进篇 | 华为VanillaNet + BiFPN突破涨点极限
一、本文介绍 本文给大家带来的改进机制是华为VanillaNet主干配合BiFPN实现融合涨点,这个主干是一种注重极简主义和效率的神经网络我也将其进行了实验, 其中的BiFPN不用介绍了从其发布到现在一直是比较热门的改进机制,其主要思想是通过多层级的特征金字塔和双向信息传递来提…...

C++初阶篇----新手进村
目录 一、什么是C二、C关键字三、命名空间3.1命名空间的定义3.2命名空间的使用 四、C输入和输出五、缺省参数5.1缺省参数的概念5.2缺省参数的分类 六、函数重载6.1函数重载的概念6.2函数重载的原理----名字修饰 七、引用7.1引用概念7.2引用特性7.3常引用7.4引用的使用7.5传值、…...

假期刷题打卡--Day26
1、MT1212乘法表 请编写一个简单程序,输出九九乘法表。输入n,就输出乘法表到n的地方。 格式 输入格式: 输入整型 输出格式: 输出整型。形式如:1*11 样例 1 输入: 5输出: 1*11 2*12 …...
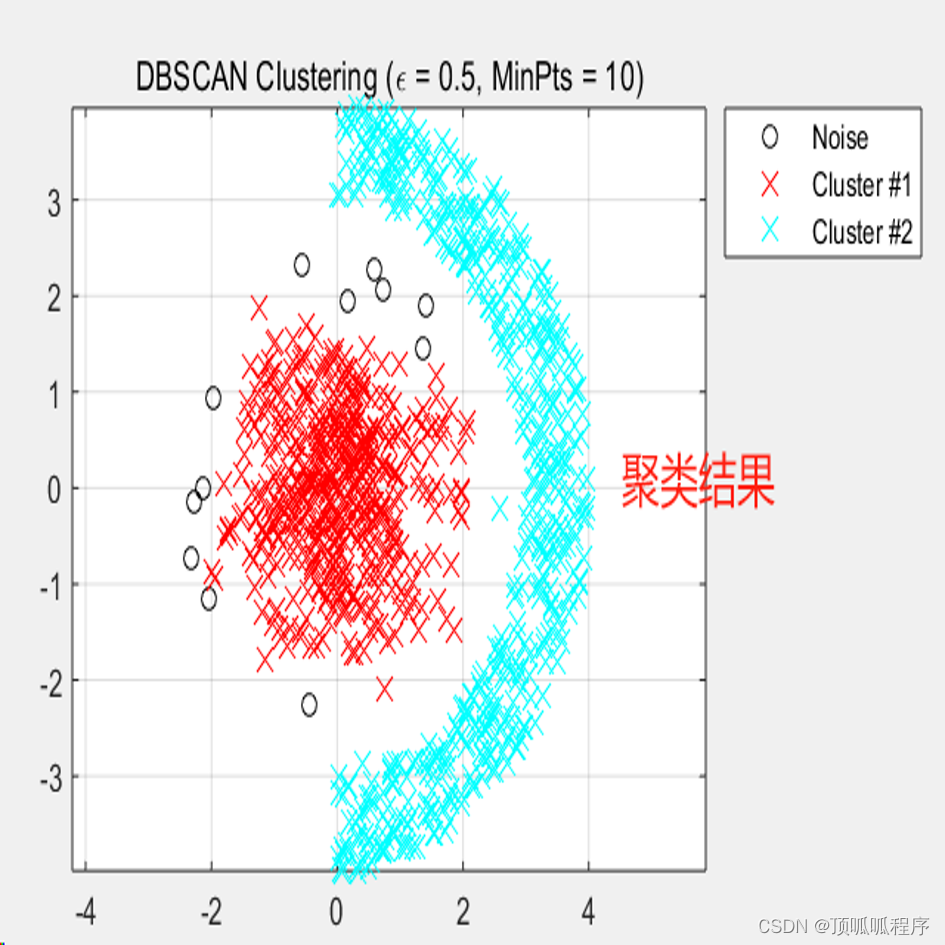
159基于matlab的基于密度的噪声应用空间聚类(DBSCAN)算法对点进行聚类
基于matlab的基于密度的噪声应用空间聚类(DBSCAN)算法对点进行聚类,聚类结果效果好,DBSCAN不要求我们指定集群的数量,避免了异常值,并且在任意形状和大小的集群中工作得非常好。它没有质心,聚类簇是通过将相邻的点连接…...

CVPR 2023: GANmouflage: 3D Object Nondetection with Texture Fields
我们使用以下6个分类标准对本文的研究选题进行分析: 1. 伪装类型: 自然伪装: 此类别关注受自然界伪装策略启发或直接复制的研究。这包括研究动物的体色、图案和纹理,为人工伪装的设计提供信息,通常以生物学真实性和有效性为目标 (例如,参考文献 [12, 19, 30, 48])。人工伪…...

【ASP.NET Core 基础知识】--部署和维护--日志记录和错误处理
一、日志记录(Logging) 1.1 日志记录的概念 日志记录是一种记录系统运行状态、活动和事件的重要机制。在软件开发和系统管理中,日志记录扮演着关键角色,用于追踪应用程序的执行过程、监视系统的健康状况、诊断问题和安全审计等。在ASP.NET Core等现代W…...

docker命令梳理
docker镜像操作 //从硬盘加入镜像 docker load -i xxx.tar //基于dockerfile构建镜像 docker build -t xxx:xxx . //查看镜像 docker images //镜像改名 docker tag //docker镜像提交到容器 //docker commit [-m“描述信息”] [-a“作者”]容器id 镜像名[:标签名] docker镜像仓…...
彩虹系统7.0免授权+精美WAP端模板源码
最低配置环境 PHP7.2 1、上传源码到网站根目录,导入数据库文件 2、修改数据库配置文件:/config.php 3、后台:/admin 账号: 4、前台用户:123456 密码:1234561...

linux系统haproxy负载均衡工具的介绍以及使用
haproxy 概述haproxy的特点haproxy算法haproxy做四层负载均衡haproxy做七层负载均衡 概述 ha-proxy是一款高性能的负载均衡软件。其专注于负载均衡这一些事情,因此与nginx比起来,负载均衡做的更好haproxy---主要是做负载均衡的7层,也可以做4…...

七、Nacos源码系列:Nacos服务发现
目录 一、服务发现 二、getServices():获取服务列表 2.1、获取服务列表 2.2、总结图 三、getInstances(serviceId):获取服务实例列表 3.1、从缓存中获取服务信息 3.2、缓存为空,执行订阅服务 3.2.1、调度更新,往线程池中…...
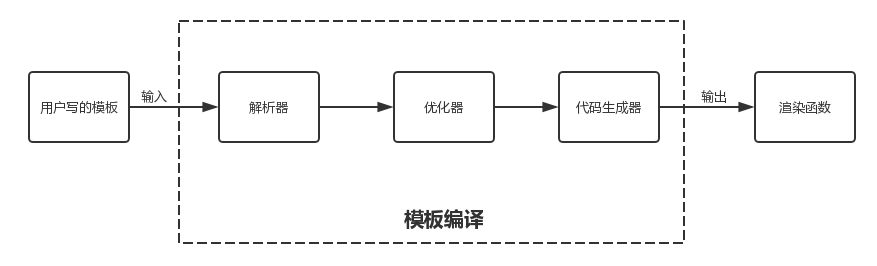
Vue源码系列讲解——模板编译篇【一】(综述)
目录 1. 前言 2. 什么是模板编译 3. 整体渲染流程 4. 模板编译内部流程 4.1 抽象语法树AST 4.2 具体流程 5. 总结 1. 前言 在前几篇文章中,我们介绍了Vue中的虚拟DOM以及虚拟DOM的patch(DOM-Diff)过程,而虚拟DOM存在的必要条件是得先有VNode&…...

【机器学习】数据清洗之识别异常点
🎈个人主页:甜美的江 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进步…...

MacOS 制作 TF 卡/ U 盘镜像
最近有张老的 TF 卡没办法直接拷贝里面的数据,于是打算利用 dd 工具直接全卡拷贝为镜像再分析里面的数据 在终端中,输入以下命令来列出所有磁盘设备: diskutil list这将显示Mac上所有的磁盘设备。你需要找到TF卡对应的设备,它通…...
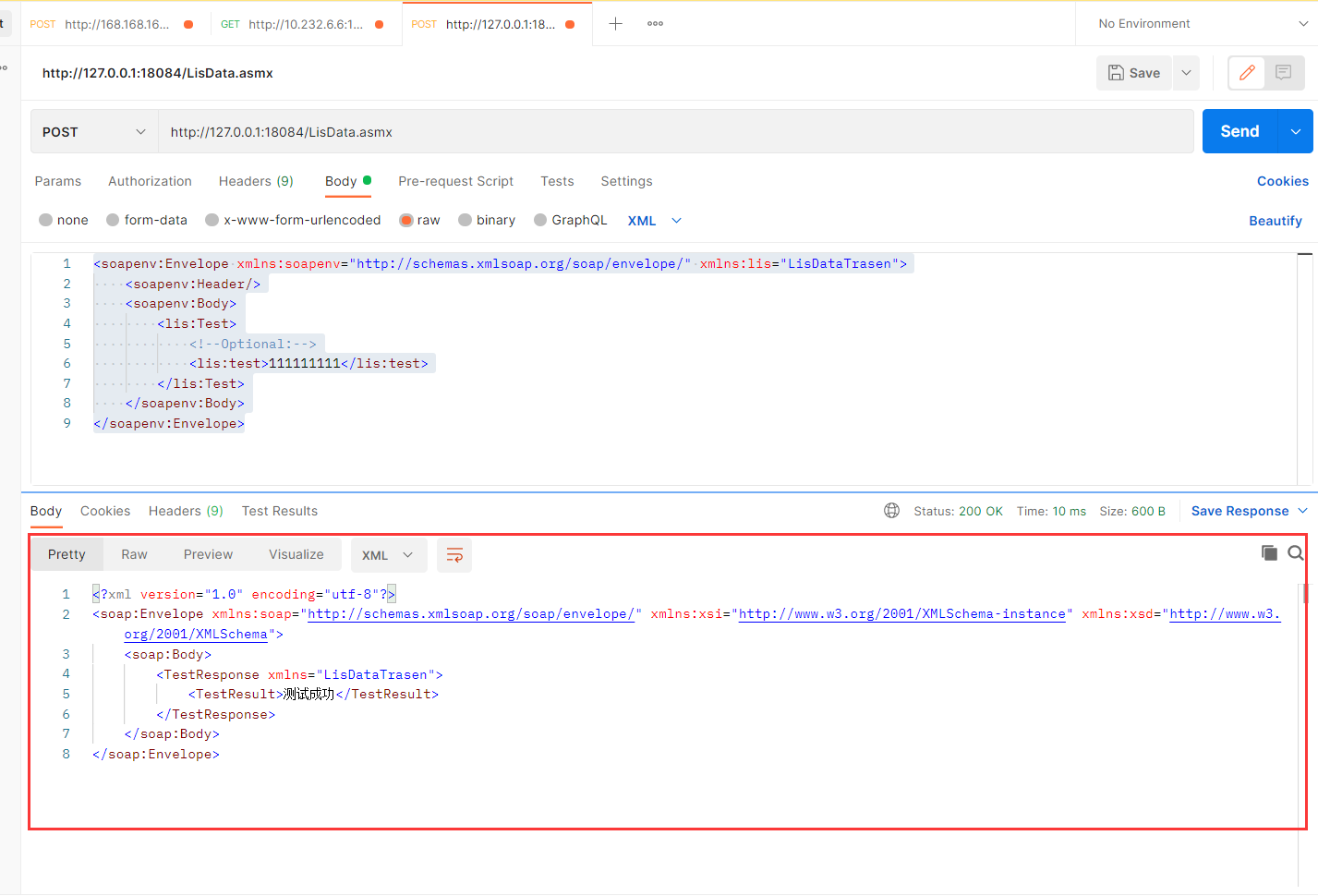
怎么用postman调用webservice(反推SoapUI)
<soapenv:Envelope xmlns:soapenv“http://schemas.xmlsoap.org/soap/envelope/” xmlns:lis“LisDataTrasen”> soapenv:Header/ soapenv:Body lis:Test lis:test111111111</lis:test> </lis:Test> </soapenv:Body> </soapenv:Envelope> Conten…...

【开源】JAVA+Vue.js实现衣物搭配系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 衣物档案模块2.2 衣物搭配模块2.3 衣物收藏模块 三、系统设计3.1 用例设计3.2 E-R图设计3.3 数据库设计3.3.1 衣物档案表3.3.2 衣物搭配表3.3.3 衣物收藏表 四、系统实现4.1 登录页4.2 衣物档案模块4.3 衣物搭配模块4.4…...

【Flask + AI】接入CHATGLM API 实现翻译接口
【Flask AI】接入CHATGLM API 实现翻译接口 最近的项目中,需要加一个翻译功能,正好chatglm4发布了,于是决定着手用它实现。 https://chatglm.cn 准备 首先,在chatglm开发者中心申请api key,这里不再赘述 其次&…...

并发事务带来的问题及解决方法
引言 在数据库系统中,事务是指一组操作被视为一个逻辑单元,要么全部执行成功,要么全部不执行,保证数据库的一致性和完整性。而并发事务则是指多个事务同时执行的情况。虽然并发事务能够提高系统的性能和吞吐量,但也会…...

CRNN介绍:用于识别图中文本的深度学习模型
CRNN:用于识别图中文本的深度学习模型 CRNN介绍:用于识别图中文本的深度学习模型CRNN的结构组成部分工作原理 CRNN结构分析卷积层(Convolutional Layers)递归层(Recurrent Layers)转录层(Transc…...

机器人运动学林沛群——变换矩阵
对于仅有移动,由上图可知: A P B P A P B o r g ^AP^BP^AP_{B org} APBPAPBorg 对于仅有转动,可得: A P B A R B P ^AP^A_BR^BP APBARBP 将转动与移动混合后,可得: 一个例子 在向量中ÿ…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
