给定n,m(200),构造一个n*m的矩阵a,使得每个4*4的子矩阵,左上角2*2的子矩阵的异或和等于右下角的,左下角的异或和等于右上角的
题目
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pb push_back
#define fi first
#define se second
#define lson p << 1
#define rson p << 1 | 1
const int maxn = 1e6 + 5, inf = 1e18 + 5, maxm = 4e4 + 5, mod = 998244353, N = 1e6;
int a[505][505], b[maxn];
// bool vis[maxn];
int n, m;
string s;
int f[maxn];bool check(){for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){if(i + 4 - 1 > n || j + 4 - 1 > m) continue;int t = a[i][j] ^ a[i][j + 1] ^ a[i + 1][j] ^ a[i + 1][j + 1];int t2 = a[i + 2][j + 2] ^ a[i + 2][j + 1 + 2] ^ a[i + 1 + 2][j + 2] ^ a[i + 1 + 2][j + 1 + 2];if(t != t2){cout << i << ' ' << j << '\n';cout << t << ' ' << t2 << '\n';return 0;}// cout << i << ' ' << j << ' ' << t << '\n';t = a[i][j + 2] ^ a[i][j + 1 + 2] ^ a[i + 1][j + 2] ^ a[i + 1][j + 1 + 2];t2 = a[i + 2][j] ^ a[i + 2][j + 1] ^ a[i + 1 + 2][j] ^ a[i + 1 + 2][j + 1];if((t != t2)){cout << i << ' ' << j << '\n';return 0;}}}return 1;
}
void ff(int x){for(int j = 15; j >= 0; j--){cout << (x >> j & 1);}cout << '\n';
}
void solve(){int res = 0;int k;int x;int q;cin >> n >> m;int add = 0;int d2 = 1LL << 30;for(int i = 1; i <= n; i += 2){add = 0;for(int j = 1; j <= m; j += 2){a[i][j] = 0 + add + (i - 1) / 2 * d2;a[i][j + 1] = 1 + add + (i - 1) / 2 * d2;a[i + 1][j] = 2 + add + (i - 1) / 2 * d2;a[i + 1][j + 1] = 3 + add + (i - 1) / 2 * d2;add += 4;}}/*把 2 * 2 的子矩阵为一组,按4*k, 4*k+14*k+2, 4*k+3 的方式构造,每一组内异或和为0,但是为了矩阵的每个数字都不同,每一行都要加上d2,第i行加(i - 1) / 2个d2*/cout << n * m << '\n';for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cout << a[i][j] << ' ';}cout << '\n';}}signed main(){ios::sync_with_stdio(0);cin.tie(0);// fac[0] = 1;// for(int i = 1; i <= N; i++){// fac[i] = fac[i - 1] * i % mod;// }// inv[N] = qpow(fac[N], mod - 2);// for(int i = N - 1; i >= 0; i--){// inv[i] = inv[i + 1] * (i + 1) % mod;// }int T = 1;cin >> T;while (T--){solve();}return 0;
}相关文章:
,构造一个n*m的矩阵a,使得每个4*4的子矩阵,左上角2*2的子矩阵的异或和等于右下角的,左下角的异或和等于右上角的)
给定n,m(200),构造一个n*m的矩阵a,使得每个4*4的子矩阵,左上角2*2的子矩阵的异或和等于右下角的,左下角的异或和等于右上角的
题目 #include <bits/stdc.h> using namespace std; #define int long long #define pb push_back #define fi first #define se second #define lson p << 1 #define rson p << 1 | 1 const int maxn 1e6 5, inf 1e18 5, maxm 4e4 5, mod 998244353…...

【开源】基于JAVA+Vue+SpringBoot的假日旅社管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统介绍2.2 QA 问答 三、系统展示四、核心代码4.1 查询民宿4.2 新增民宿评论4.3 查询民宿新闻4.4 新建民宿预订单4.5 查询我的民宿预订单 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVueSpringBootMySQL的假日旅社…...
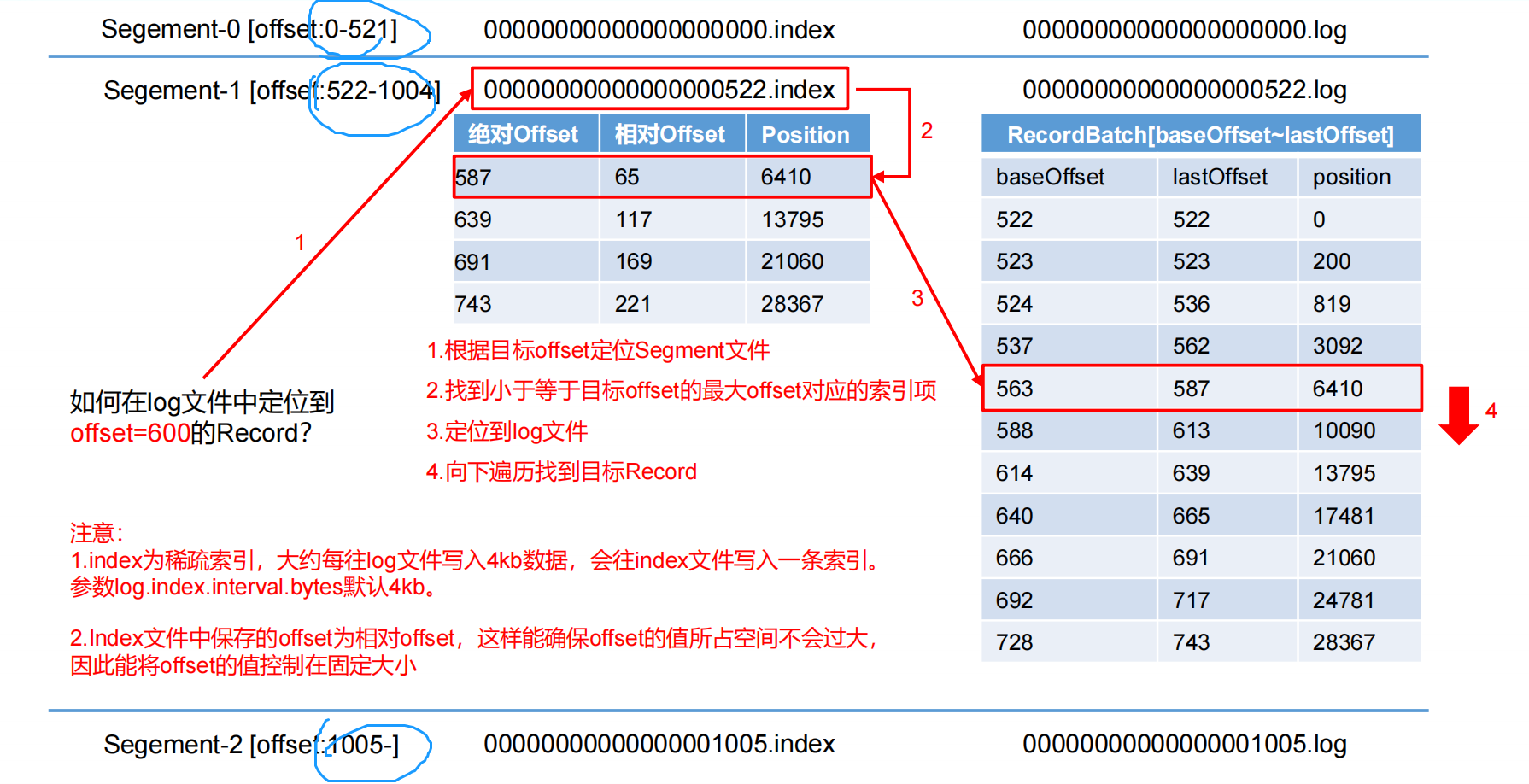
kafka 文件存储机制
文章目录 1. 思考四个问题:1.1 topic中partition存储分布:1.2 partiton中文件存储方式:1.3 partiton中segment文件存储结构:1.4 在partition中如何通过offset查找message: 2. kafka日志存储参数配置 Topic是逻辑上的概念ÿ…...

引入BertTokenizer出现OSError: Can‘t load tokenizer for ‘bert-base-uncased‘.
今天在跑一个模型的时候出现该报错,完整报错为: OSError: Cant load tokenizer for bert-base-uncased. If you were trying to load it from https://huggingface.co/models, make sure you dont have a local directory with the same name. Otherwis…...
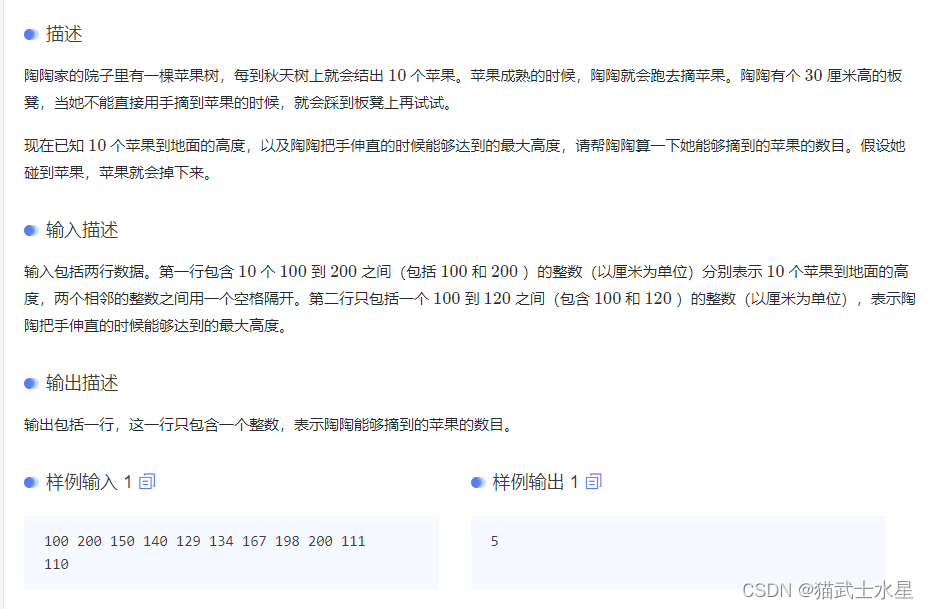
陶陶摘苹果C++
题目: 代码: #include<iostream> using namespace std; int main(){//一、分析问题//已知:10 个苹果到地面的高度a[10],陶陶把手伸直的时候能够达到的最大高度height//未知:陶陶能够摘到的苹果的数目sum。//关系ÿ…...

STM32F1 引脚重映射功能
STM32 端口引脚重映射 文章目录 STM32 端口引脚重映射前言1、查阅芯片数据手册1.1 串口引脚重映射描述 2、代码部分2.1 核心代码部分 3、实验现象4、总结 前言 在写程序时遇到想要的端口功能,而这个引脚又被其它的功能占用了无法删除掉或直接使用,这种情…...
)
c语言的各类输出函数(带完善更新)
printf double x; x 218.82631; printf("%-6.2e\n", x);printf(“%-6.2e\n”, x);使用printf函数以指定的格式输出x的值。"%-6.2e"是格式化字符串,其中: %e表示以科学计数法的形式输出浮点数。 6表示输出的总宽度为6个字符&#…...

【linux温故】CFS调度
写在前面 网上关于CFS 调度器的文章多如牛毛,没必要自己写。很多文章写的都非常好。 很多文章里,关键的技术点,都是一样的,只是各个文章说法不一样。 掌握了核心的,关键的,其他的,如果工作中…...
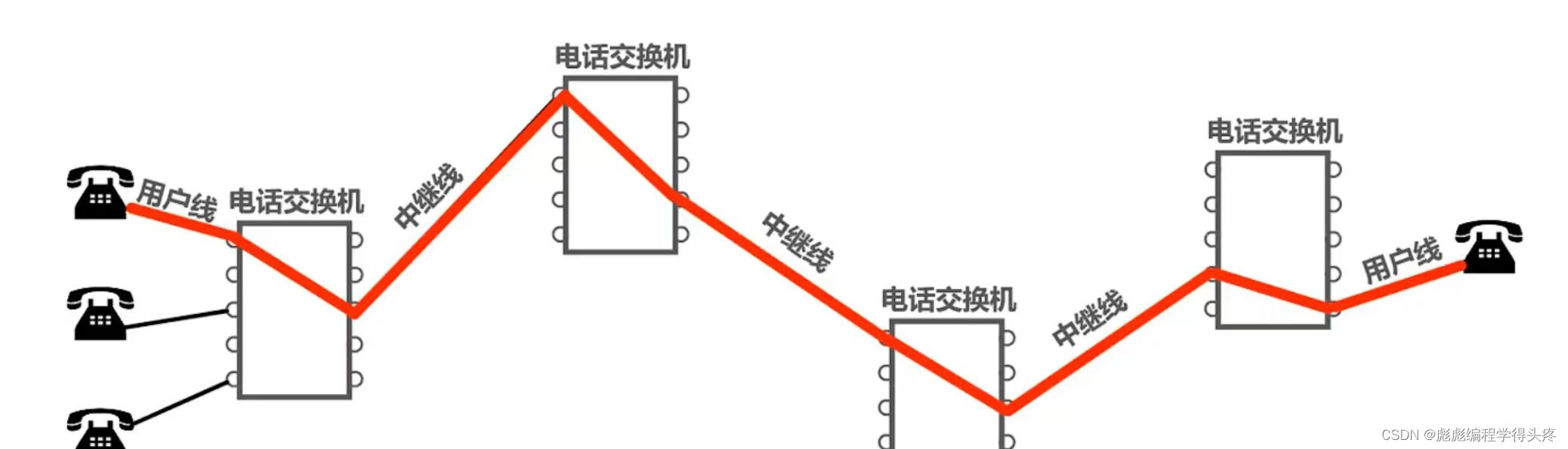
计算机网络之一
目录 1.因特网概述 1.1网络、互连网(互联网)和因特网 1.2.因特网发展的三个阶段 1.3基于ISP的三层架构的因特网 1.4.因特网的组成 2.三种交换方式 2.1电路交换 2.2分组交换 1.因特网概述 1.1网络、互连网(互联网)和因特网…...
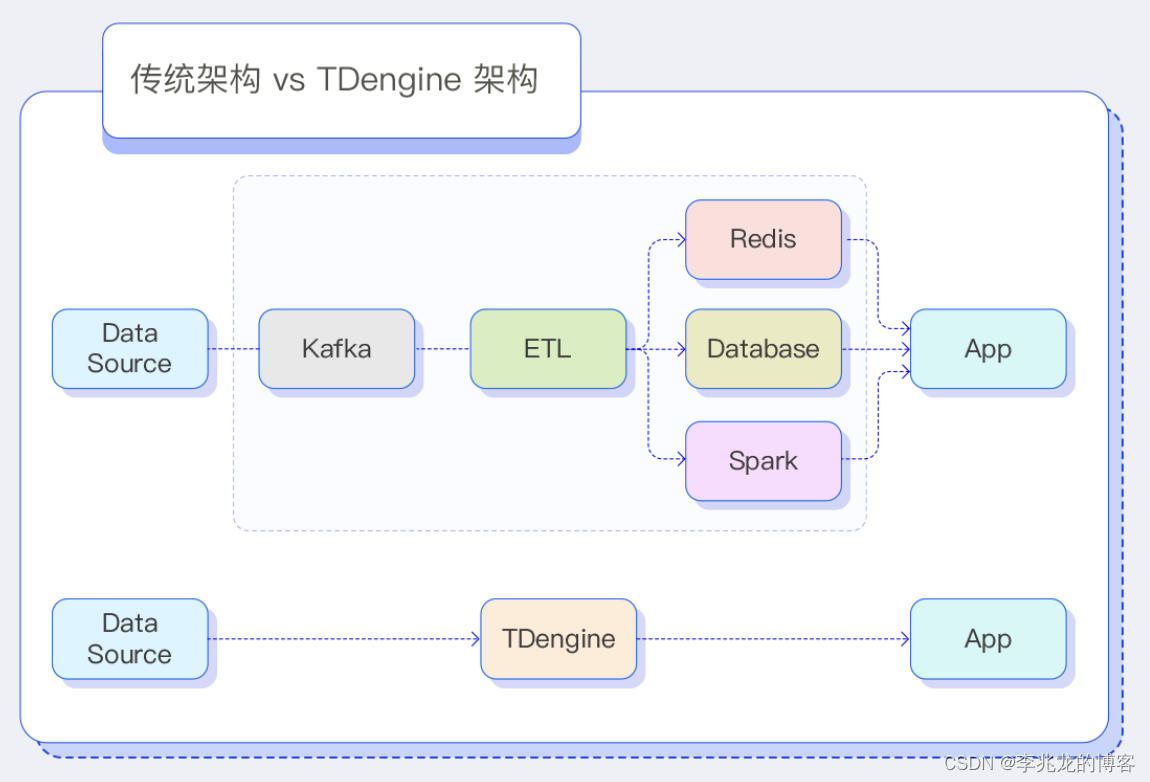
从一到无穷大 #23 《流计算系统图解》书评
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 本作品 (李兆龙 博文, 由 李兆龙 创作),由 李兆龙 确认,转载请注明版权。 文章目录 引言内容总结 引言 春节假期回到家里断然是不会有看纸质书的时间的。造化弄人&#…...

华为问界M9:领跑未来智能交通的自动驾驶黑科技
华为问界M9是一款高端电动汽车,其自动驾驶技术是该车型的重要卖点之一。华为在问界M9上采用了多种传感器和高级算法,实现了在不同场景下的自动驾驶功能,包括自动泊车、自适应巡航、车道保持、自动变道等。 华为问界M9的自动驾驶技术惊艳之处…...

Java图形化界面编程——弹球游戏 笔记
Java也可用于开发一些动画。所谓动画,就是间隔一定的时间(通常小于0 . 1秒 )重新绘制新的图像,两次绘制的图像之间差异较小,肉眼看起来就成了所谓的动画 。 为了实现间隔一定的时间就重新调用组件的 repaint()方法,可以借助于…...

浅谈人工智能之深度学习~
目录 前言:深度学习的进展 一:深度学习的基本原理和算法 二:深度学习的应用实例 三:深度学习的挑战和未来发展方向 四:深度学习与机器学习的关系 五:深度学习与人类的智能交互 悟已往之不谏࿰…...
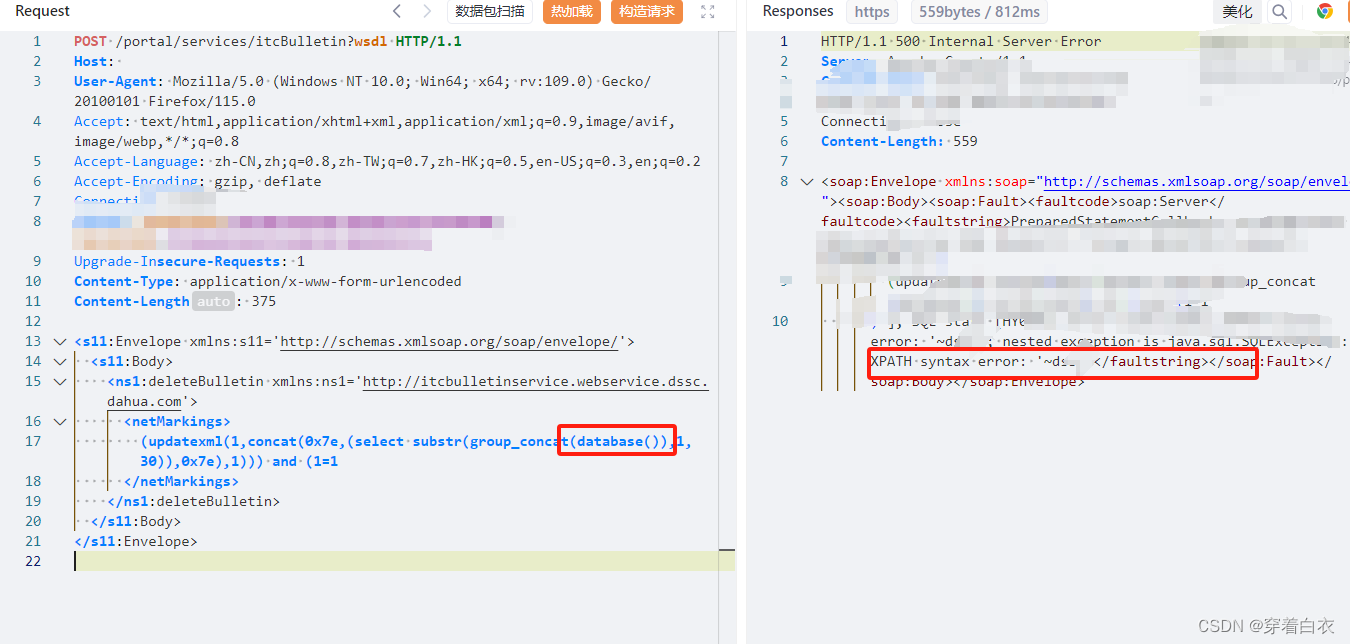
【复现】大华 DSS SQL 注入漏洞_46
目录 一.概述 二 .漏洞影响 三.漏洞复现 1. 漏洞一: 四.修复建议: 五. 搜索语法: 六.免责声明 一.概述 大华DSS是大华的大型监控管理应用平台,支持几乎所有涉及监控等方面的操作,支持多级跨平台联网等操作。 可…...

Python 中的断点类型详解
前言 在 Python 中,断点是一种在代码中设置的标记,用于在程序执行过程中停止或中断程序的执行,以便调试和查看程序的内部状态。断点是调试工具的关键组成部分,能够帮助开发者定位和解决代码中的错误。本文将详细介绍 Python 中的…...
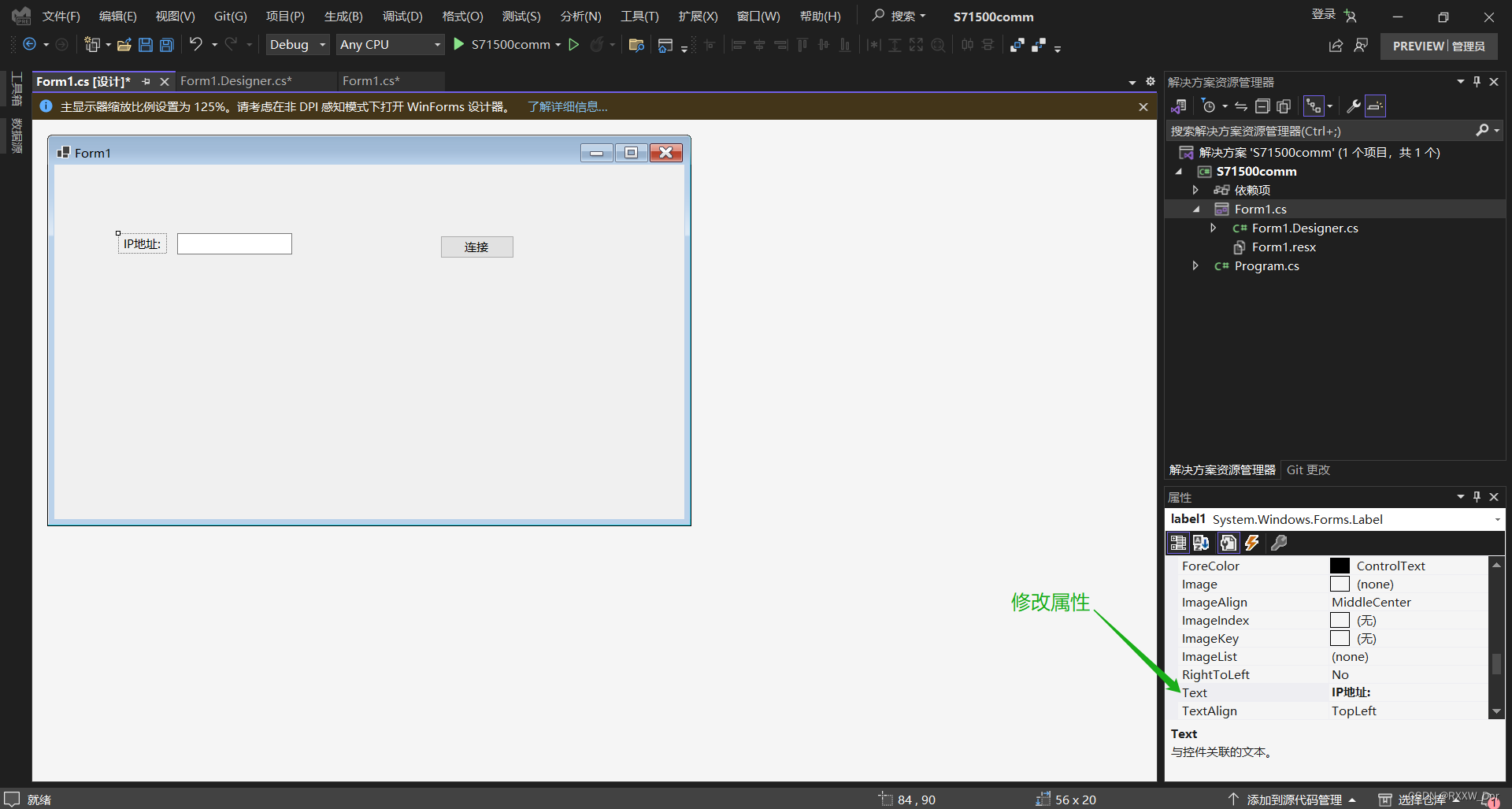
一步步建立一个C#项目(连续读取S7-1200PLC数据)
这篇博客作为C#的基础系列,和大家分享如何一步步建立一个C#项目完成对S7-1200PLC数据的连续读取。首先创建一个窗体应用。 1、窗体应用 2、配置存储位置 3、选择框架 拖拽一个Button,可以选择视图菜单---工具箱 4、工具箱 拖拽Lable控件和TextBook控件 5、拖拽控件 接下来…...
Hive窗口函数详解
一、 窗口函数知识点 1.1 窗户函数的定义 窗口函数可以拆分为【窗口函数】。窗口函数官网指路: LanguageManual WindowingAndAnalytics - Apache Hive - Apache Software Foundationhttps://cwiki.apache.org/confluence/display/Hive/LanguageManual%20Windowing…...
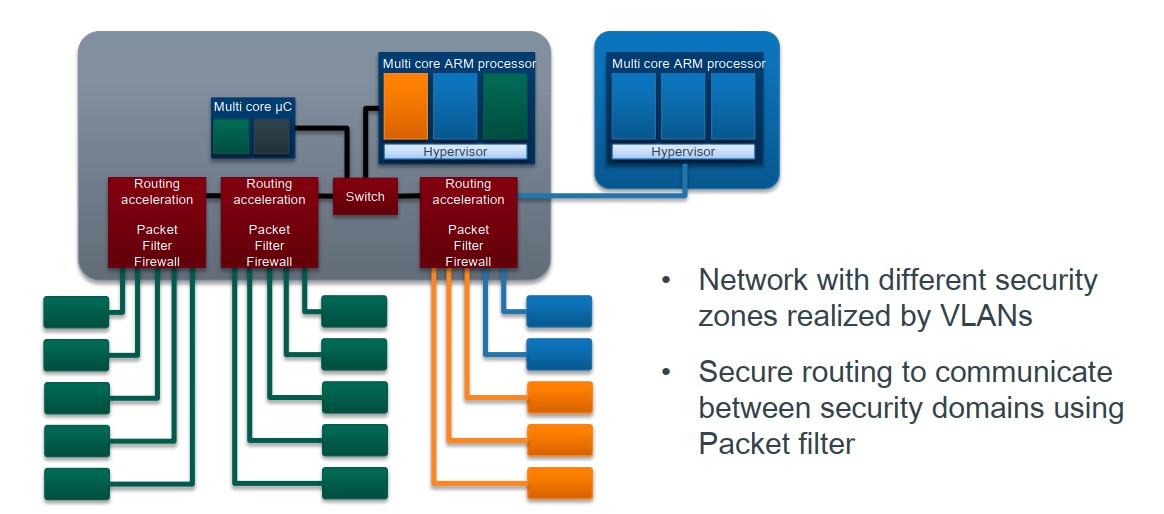
车载电子电器架构 —— 电子电气系统功能开发
车载电子电器架构 —— 电子电气系统功能开发 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 本就是小人物,输了就是输了,不要在意别人怎么看自己。江湖一碗茶,喝完再挣扎,出门靠自己,四海皆…...

LeetCode--代码详解 7.整数反转
7.整数反转 题目 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 示例 …...

《统计学简易速速上手小册》第6章:多变量数据分析(2024 最新版)
文章目录 6.1 主成分分析(PCA)6.1.1 基础知识6.1.2 主要案例:客户细分6.1.3 拓展案例 1:面部识别6.1.4 拓展案例 2:基因数据分析 6.2 聚类分析6.2.1 基础知识6.2.2 主要案例:市场细分6.2.3 拓展案例 1&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
