机器学习——流形学习
流形学习是一种在机器学习领域中用于理解和分析数据的技术。它的核心思想是,尽管我们通常将数据表示为高维空间中的向量,但实际上数据可能具有较低维度的内在结构,这种结构被称为流形。流形学习的目标是发现并利用数据的这种潜在结构,以便更好地理解和处理数据。
一些基本概念开始:
1. 流形
流形是一种数学概念,指的是局部类似于欧几里德空间的空间。简单来说,流形可以理解为在高维空间中弯曲或扭曲的低维子空间。例如,二维球面就是三维空间中的一个流形,虽然它是三维的,但局部上看起来类似于二维平面。
2. 高维数据
在现实世界中,我们通常会面对高维数据,比如图像、文本、传感器数据等。这些数据由许多特征组成,每个特征都可以看作是数据空间中的一个维度。
3. 问题
在高维空间中进行数据分析和建模可能会面临一些挑战。例如,维度灾难会导致数据稀疏性和过拟合问题,而高维数据的可视化和理解也变得困难。
4. 流形学习的目标
流形学习的目标是通过发现数据的低维流形结构来解决这些问题。它通过将高维数据映射到一个更低维度的流形空间中,从而提供更紧凑和具有判别性的数据表示。这种表示通常更适合用于可视化、分类、聚类和其他机器学习任务。
5. 流形学习的方法
流形学习的方法通常包括以下步骤:
-
相似度/距离计算: 首先,计算数据点之间的相似度或距离,以衡量它们之间的关系。
-
局部近邻搜索: 对于每个数据点,找到其在高维空间中的局部近邻。
-
流形重建: 基于局部近邻关系,通过一些数学技术(如局部线性嵌入、等度量映射等)来估计数据的低维流形结构。
-
降维映射: 将高维数据映射到低维流形空间中,以得到更紧凑和具有判别性的表示。
6. 应用
流形学习在数据可视化、特征提取、数据压缩和降维、异常检测等领域都有广泛的应用。常见的流形学习算法包括局部线性嵌入(Locally Linear Embedding, LLE)、等度量映射(Isomap)、拉普拉斯特征映射(Laplacian Eigenmaps)、t-分布邻近嵌入(t-Distributed Stochastic Neighbor Embedding, t-SNE)等。
通过流形学习,我们可以更好地理解和处理高维数据,从而提取出数据的有效特征和结构。
更直白易懂的解释
流形学习是一种处理高维数据的方法,可以帮助我们更好地理解和分析数据。想象一下你有一堆数据点,这些点在很多维度上有信息,比如一张图片,它不仅仅有长和宽,还有颜色深浅等等,这些都是不同的维度。高维意味着数据在很多不同的方面都有变化,这使得直接观察和理解数据变得非常困难。
流形学习的核心思想是,虽然这些数据点在高维空间中分布,但实际上它们可能会沿着某种低维的结构排列。这就好比一张纸是二维的,但你可以把它卷成一个筒,或者折成各种形状,这些形状在三维空间中展开,但纸的本质仍然是二维的。流形学习就是要找到这种低维的**“本质结构”**。
为了让人更容易理解,我们可以用一个简单的比喻:想象你在一个黑暗的山洞里,手里只有一支手电筒。你的任务是弄清楚山洞的形状。手电筒照亮的部分就像是你通过观察数据获得的信息,虽然你不能一眼看到整个山洞的形状,但通过在不同位置照亮,你可以逐渐理解山洞的布局。流形学习就像是这个过程,通过从不同角度“照亮”数据,帮助我们理解数据的内在结构,即便这些数据本身是在很高的维度上分布的。
在实践中,流形学习可以帮助我们在降低数据的维度的同时,保留数据的重要特征,这样不仅可以让数据更容易被理解和分析,还可以提高数据处理的效率。
总结
简单来说,流形学习就是一种找到数据内在结构的智能方式,使得我们可以更简单地处理和理解复杂的高维数据。
补充:
微分流形
微分流形是数学中的一个概念,用于描述那些在局部看起来像欧几里得空间(即我们熟悉的二维平面或三维空间)的空间,但整体上可能有复杂的形状和结构。可以将微分流形想象成一个可以被平滑弯曲的形状,比如地球的表面。虽然地球是一个三维对象,但其表面(忽略山脉和海洋的高低起伏)可以被看作是一个二维的微分流形,因为在任何一个小的区域内,它都近似于一个平面。
李群
李群以挪威数学家索菲斯·李的名字命名,是一种特殊的群,它既是一个群(一个包含一系列元素和一个元素间组合规则的数学结构,其中每个元素都有一个逆,且组合规则满足某些基本性质,如结合律)也是一个微分流形。这意味着李群的元素可以连续地变化,并且这种变化可以用微分方程来描述。李群在物理学中非常重要,因为它们能够描述对称性,比如旋转、平移等操作。一个简单的例子是地球上的所有可能的旋转,这些旋转构成了一个李群,因为你可以连续地从一个旋转过渡到另一个旋转,并且这些旋转操作遵循群的规则。
李代数
李代数是与李群紧密相关的数学结构,它描述了李群元素的无穷小变化,可以被看作是李群结构的“切空间”(在某点的切线空间,描述在该点附近李群元素如何变化)。如果李群是通过一组连续变换描述的对称性,那么李代数则描述了这些变换开始改变时的行为。简单来说,如果你把李群想象成一个可以连续变化的对象集合,那么李代数就描述了这些变化在非常小的尺度上是如何进行的。例如,在物理学中,李代数帮助人们理解基本粒子的对称性和守恒律。
用更通俗的语言,如果说李群是描述一系列动作(如转动一个球)的规则集合,那么李代数就是描述这些动作开始如何微小变化的规则。它们是理解复杂系统变化规律的强大工具,尤其是在物理学和几何学中。
相关文章:

机器学习——流形学习
流形学习是一种在机器学习领域中用于理解和分析数据的技术。它的核心思想是,尽管我们通常将数据表示为高维空间中的向量,但实际上数据可能具有较低维度的内在结构,这种结构被称为流形。流形学习的目标是发现并利用数据的这种潜在结构…...
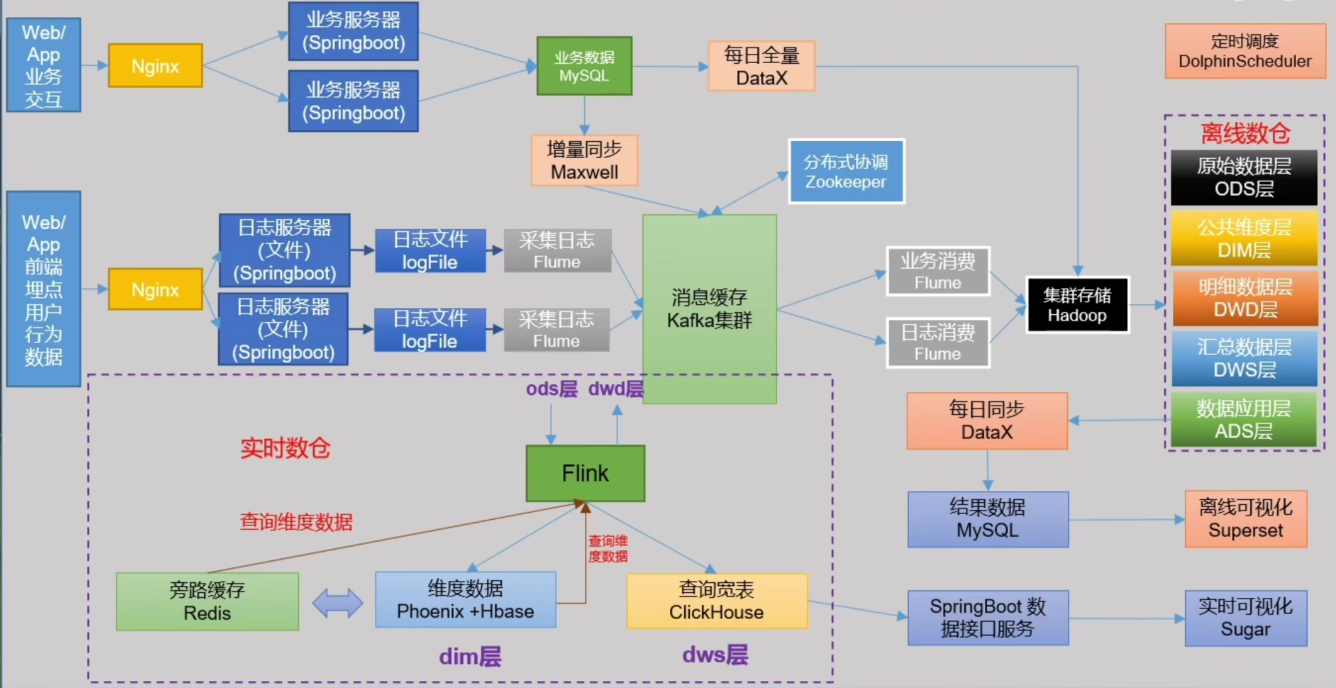
离线数仓(一)【数仓概念、需求架构】
前言 今天开始学习数仓的内容,之前花费一年半的时间已经学完了 Hadoop、Hive、Zookeeper、Spark、HBase、Flume、Sqoop、Kafka、Flink 等基础组件。把学过的内容用到实践这是最重要的,相信会有很大的收获。 1、数据仓库概念 1.1、概念 数据仓库&#x…...

物联网测试:2024 年的最佳实践和挑战
据 Transforma Insights 称,到 2030 年,全球广泛使用的物联网 (IoT) 设备预计将增加近一倍,从 151 亿台增至 290 亿台。这些设备以及智能汽车、智能手机等广泛应用于各种官僚机构。 健康视频监视器、闹钟以及咖啡机和冰箱等最受欢迎的家用电器…...

蓝桥杯Web应用开发-CSS3 新特性
CSS3 新特性 专栏持续更新中 在前面我们已经学习了元素选择器、id 选择器和类选择器,我们可以通过标签名、id 名、类名给指定元素设置样式。 现在我们继续选择器之旅,学习 CSS3 中新增的三类选择器,分别是: • 属性选择器 • 子…...

MongoDB聚合:$unionWith
$unionWith聚合阶段执行两个集合的合并,将两个集合的管道结果合并到一个结果集传送到下一个阶段。合并后的结果文档的顺序是不确定的。 语法 { $unionWith: { coll: "<collection>", pipeline: [ <stage1>, ... ] } }要包含集合的所有文档不…...

人工智能三子棋-人机对弈-人人对弈,谁会是最终赢家?
✅作者简介:大家好我是原始豌豆,感谢支持。 🆔本文由 原始豌豆 原创 CSDN首发🐒 如需转载还请通知⚠ 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:C语言项目实践…...
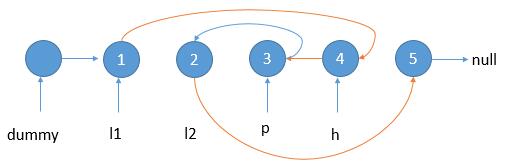
【leetcode热题100】反转链表 II
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出:[1,4,3,2…...

谷歌 DeepMind 联合斯坦福推出了主从式遥操作双臂机器人系统增强版ALOHA 2
谷歌 DeepMind 联合斯坦福推出了 ALOHA 的增强版本 ——ALOHA 2。与一代相比,ALOHA 2 具有更强的性能、人体工程学设计和稳健性,且成本还不到 20 万元人民币。并且,为了加速大规模双手操作的研究,ALOHA 2 相关的所有硬件设计全部开…...

金融行业专题|证券超融合架构转型与场景探索合集(2023版)
更新内容 更新 SmartX 超融合在证券行业的覆盖范围、部署规模与应用场景。新增操作系统信创转型、Nutanix 国产化替代、网络与安全等场景实践。更多超融合金融核心生产业务场景实践,欢迎阅读文末电子书。 在金融行业如火如荼的数字化转型大潮中,传统架…...

【C语言】C的整理记录
前言 该笔记是建立在已经系统学习过C语言的基础上,笔者对C语言的知识和注意事项进行整理记录,便于后期查阅,反复琢磨。C语言是一种面向过程的编程语言。 原想在此阐述一下C语言的作用,然而发觉这些是编程语言所共通的作用&#…...
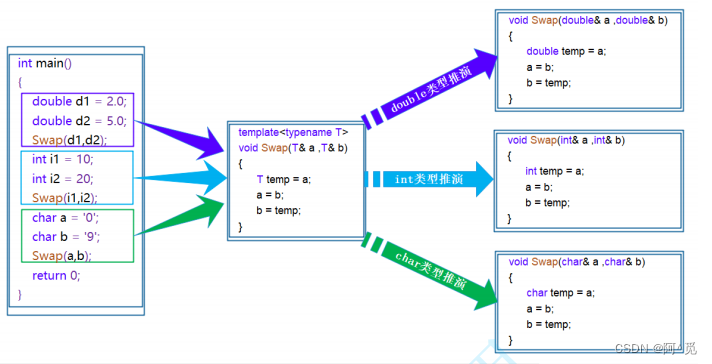
C/C++模板初阶
目录 1. 泛型编程 2. 函数模板 2.1 函数模板概念 2.1 函数模板格式 2.3 函数模板的原理 2.4 函数模板的实例化 2.5 模板参数的匹配原则 3. 类模板 3.1 类模板的定义格式 3.2 类模板的实例化 1. 泛型编程 如何实现一个通用的交换函数呢? void Swap(int&…...
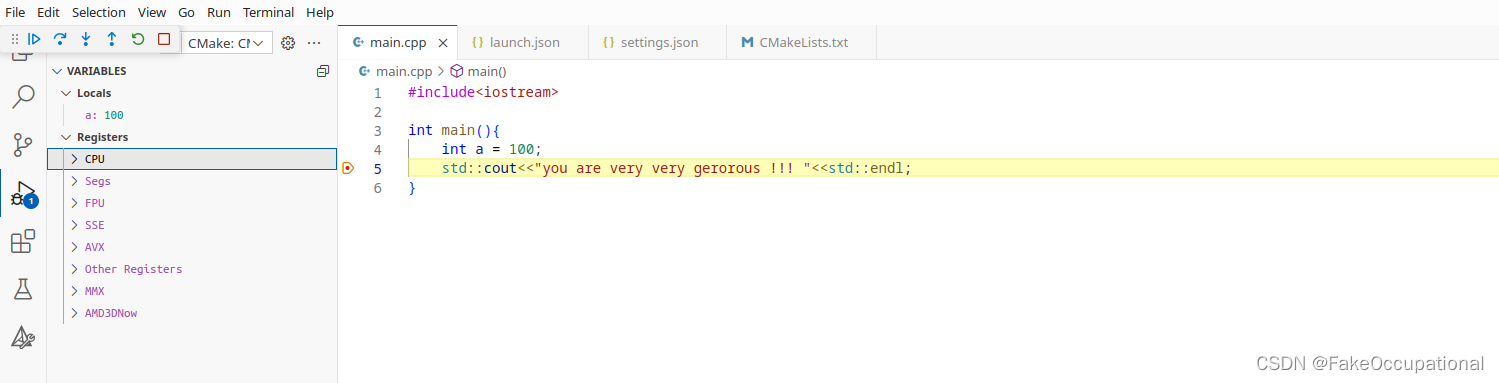
linux系统下vscode portable版本的c++/Cmake环境搭建001
linux系统下vscode portable版本的Cmake环境搭建 vscode portable 安装安装基本工具安装 build-essential安装 CMake final script code安装插件CMake Tools & cmakeC/C Extension Pack Testsettings,jsonCMakeLists.txt调试和运行工具 CG 目的:希望在获得一个新…...

【QT+QGIS跨平台编译】之三十一:【FreeXL+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、FreeXL介绍二、文件下载三、文件分析四、pro文件五、编译实践一、FreeXL介绍 【FreeXL跨平台编译】:Windows环境下编译成果(支撑QGIS跨平台编译,以及二次研发) 【FreeXL跨平台编译】:Linux环境下编译成果(支撑QGIS跨平台编译,以及二次研发) 【FreeXL跨平台…...

2024年 前端JavaScript入门到精通 第一天
主要讲解JavaScript核心知识,包含最新ES6语法,从基础到API再到高级。让你一边学习一边练习,重点知识及时实践,同时每天安排大量作业,加深记忆,巩固学习成果。 1.1 基本软件与准备工作 1.2 JavaScript 案例 …...

155基于matlab 的形态学权重自适应图像去噪
基于matlab 的形态学权重自适应图像去噪;通过串并联的滤波降噪对比图,说明并联降噪的优越性。输出降噪前后图像和不同方法的降噪情况的信噪比。程序已调通,可直接运行。 155matlab 自适应图像降噪 串并联降噪 (xiaohongshu.com)...
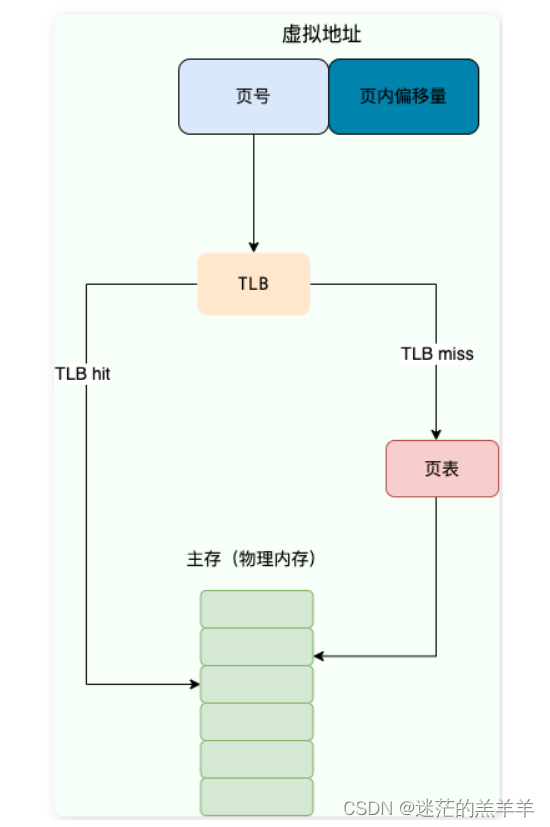
操作系统——内存管理(附带Leetcode算法题LRU)
目录 1.内存管理主要用来干什么? 2.什么是内存碎片? 3.虚拟内存 3.1传统存储管理方式的缺点? 3.2局部性原理 3.3什么是虚拟内存?有什么用? 3.3.1段式分配 3.3.2页式分配 3.3.2.1换页机制 3.3.2.2页面置换算法…...

I/O多路复用简记
IO多路复用(服务器如何处理多个socket的同时数据传输):1、select。2、poll。3、epoll。 select使用bitmap存socket文件描述符,由bitmap槽位的每一位为0或1决定对应序的socket连接是否有数据到来。由单线程(多线程处理每…...

SPECCPU2017操作说明
1、依赖包下载 yum install gcc* gfortran* 2、将软件包放至被测机器 3、增加权限 chmod X install.sh 4、运行安装 ./install.sh 5、运行 引入编译时所需的环境变量和相关库文件 source shrc 进入/spec2017,执行 ./runcpu -c ../config/Example-gcc-linux-ar…...

openresty (nginx)快速开始
文章目录 一、什么是openresty?二、openresty编译安装1. 编译安装命令1.1 编译完成后路径1.2 常用编译选项解释 2. nginx配置文件配置2.1 nginx.conf模板 3. nginx常见配置一个站点配置多个域名nginx配置中location匹配规则 三、OpenResty工作原理OpenResty工作原理…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...