【MATLAB源码-第137期】基于matlab的NOMA系统和OFDMA系统对比仿真。
操作环境:
MATLAB 2022a
1、算法描述
NOMA(非正交多址)和OFDMA(正交频分多址)是两种流行的无线通信技术,广泛应用于现代移动通信系统中,如4G、5G和未来的6G网络。它们的设计目标是提高频谱效率、支持更多的用户、实现更高的数据传输速率,并满足不断增长的移动数据通信需求。在本文中,我们将详细探讨NOMA和OFDMA的原理、特点、优缺点以及它们在通信系统中的应用。
NOMA(非正交多址)
NOMA是一种允许多个用户在相同的时间、频率资源上进行通信的技术,通过在功率域(或者码域)上分离用户来实现多用户接入。与传统的正交接入方法相比,NOMA能够显著提高频谱利用率和系统容量。
原理
NOMA的核心原理是基于功率域的多址接入。在发送端,NOMA系统通过分配不同的功率水平给不同的用户信号,然后将这些信号叠加在一起发送。由于不同用户的信号具有不同的功率水平,接收端可以利用成功干扰消除(SIC)技术来分离这些信号。在SIC过程中,接收器首先检测并解码功率最高的用户信号,然后从叠加信号中减去已解码的信号,接着解码下一个功率水平的信号,依此类推,直到所有用户的信号都被成功解码。
特点
- 高频谱效率:NOMA通过在功率域共享相同的频谱资源,允许多个用户同时传输数据,从而提高了频谱的使用效率。
- 灵活的用户接入:NOMA可以根据用户的信道条件和服务质量需求灵活地分配功率资源,从而支持更多的用户接入和更公平的服务。
- 兼容性和可扩展性:NOMA可以与现有的无线通信系统兼容,并且可以通过调整功率分配策略来适应不同的网络需求和用户密度。
应用
NOMA技术已经成为5G网络中增强移动宽带(eMBB)和大规模机器类通信(mMTC)场景的关键技术之一。通过使用NOMA,网络运营商可以在不增加额外频谱资源的情况下,支持更多的用户和服务,提高网络的吞吐量和覆盖范围。
OFDMA(正交频分多址)
OFDMA是一种基于正交频分复用(OFDM)的多址技术,它将可用的频谱资源划分为多个正交的子载波,每个子载波可以独立承载一个用户的信号。OFDMA通过在频率域上分配不同的子载波给不同的用户,来实现多用户接入和数据传输。
原理
在OFDMA系统中,整个带宽被划分为多个正交子载波,每个子载波都可以独立调制和传输数据。通过为不同的用户分配不同的子载波组,系统可以在同一时间内支持多个用户的数据传输。OFDMA技术利用了OFDM的所有优点,包括高频谱效率、抗频率选择性衰落和简化的信道均衡处理。
特点
结论
NOMA和OFDMA分别代表了功率域和频率域多用户接入技术的前沿。它们各自拥有独特的优势和应用场景,为满足不断增长的无线通信需求提供了有效的解决方案。随着5G网络的不断演进和6G技术的研究,我们可以预见NOMA和OFDMA将继续发挥重要作用,特别是在提高频谱利用率、支持大规模设备接入和实现高质量通信服务方面。未来的通信系统将可能集成这两种技术的优点,以实现更高效、更灵活、更可靠的无线通信服务。
- 高效的频谱利用:通过将带宽划分
为多个正交子载波,OFDMA可以有效地利用频谱资源,支持大量用户同时接入网络,同时减少信号之间的干扰。
- 灵活的资源分配:OFDMA允许网络根据用户需求和信道状况灵活分配子载波,支持动
态调整资源分配策略,以优化网络性能和用户体验。
- 改善的信道容量和覆盖范围:通过使用多个子载波,OFDMA能够更好地适应信道的频率选择性衰落,提高信道容量和数据传输的可靠性。此外,它还支持低功耗传输,有助于扩大网络覆盖范围。
-
应用
OFDMA技术是4G LTE和5G NR网络的核心组成部分。它为这些网络提供了高效、灵活的多用户接入机制,使得它们能够支持大量的并发用户和各种服务类型,如视频流、在线游戏和物联网(IoT)应用。OFDMA的引入显著提高了网络的吞吐量和效率,同时降低了延迟,改善了用户体验。
NOMA与OFDMA的比较
虽然NOMA和OFDMA都旨在提高无线通信系统的频谱效率和用户接入能力,但它们在技术实现和应用场景上有着本质的不同。
- 技术原理差异:NOMA侧重于功率域的多用户接入,通过不同的功率水平实现用户间的区分;而OFDMA则利用频率域的正交子载波来分隔用户,依靠子载波的分配实现多用户接入。
- 性能优化方向:NOMA更适合于用户密度高、需求多样化的场景,能够在不增加额外频谱资源的情况下,通过优化功率分配策略来提升系统容量和用户公平性。相反,OFDMA通过灵活的子载波分配机制,在保持高频谱效率的同时,优化了网络的容量和覆盖范围。
- 复杂度和实现成本:NOMA技术在接收端需要复杂的信号处理技术(如SIC),这增加了用户设备的处理复杂度和能耗。OFDMA的实现相对简单,但需要精细的资源调度策略来最大化性能。
- 兼容性和未来发展:OFDMA已经在4G和5G网络中得到广泛应用,而NOMA被视为5G及以后网络技术的补充和发展方向之一,特别是在提高系统容量和用户公平性方面显示出其潜力。
2、仿真结果演示
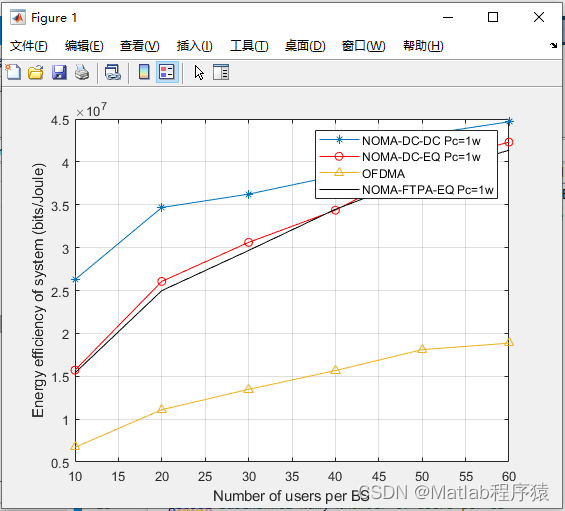




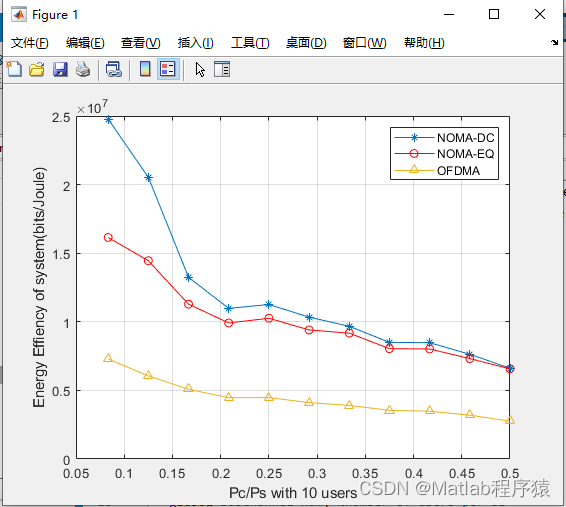
3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片
相关文章:

【MATLAB源码-第137期】基于matlab的NOMA系统和OFDMA系统对比仿真。
操作环境: MATLAB 2022a 1、算法描述 NOMA(非正交多址)和OFDMA(正交频分多址)是两种流行的无线通信技术,广泛应用于现代移动通信系统中,如4G、5G和未来的6G网络。它们的设计目标是提高频谱效…...

【FPGA Verilog】各种加法器Verilog
1bit半加器adder设计实例 module adder(cout,sum,a,b); output cout; output sum; input a,b; wire cout,sum; assign {cout,sum}ab; endmodule 解释说明 (1)assign {cout,sum}ab 是连续性赋值 对于线网wire进行赋值,必须以assign或者dea…...
)
【MySQL】-21 MySQL综合-7(MySQL主键+MySQL外检约束+MySQL唯一约束+MySQL检查约束)
MySQL主键MySQL外检约束MySQL唯一约束MySQL检查约束 MySQL主键选取设置主键约束的字段在创建表时设置主键约束在创建表时设置复合主键在修改表时添加主键约束 MySQL外键约束选取设置 MySQL 外键约束的字段在创建表时设置外键约束在修改表时添加外键约束删除外键约束 MySQL唯一约…...
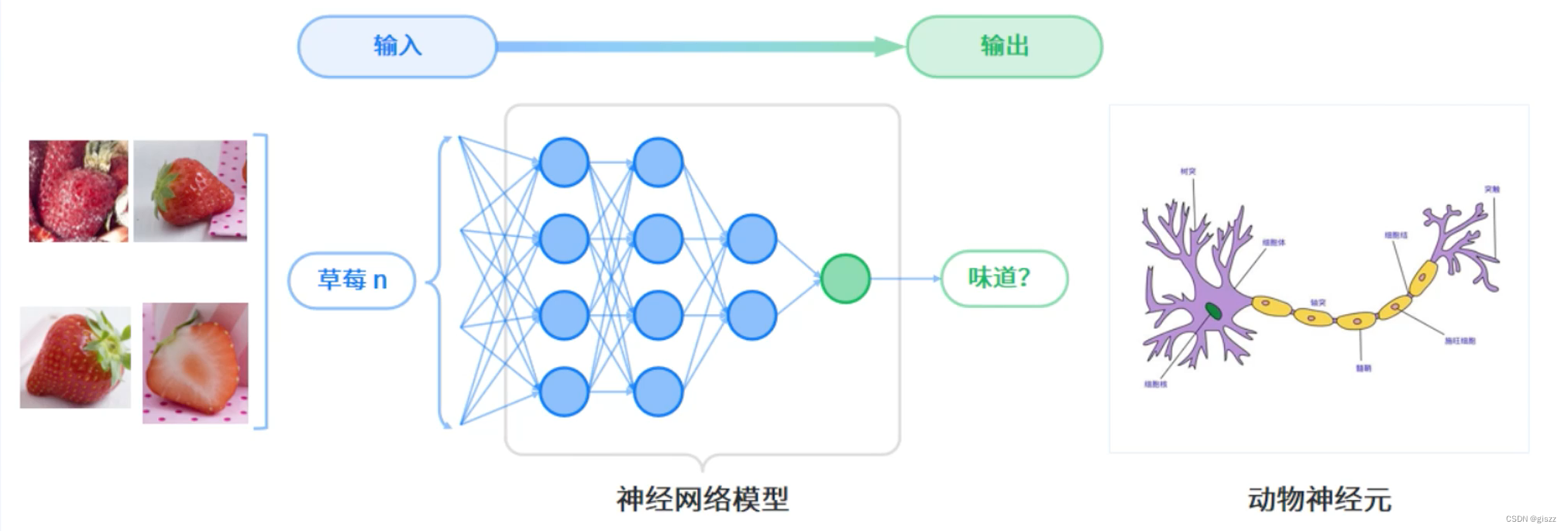
【大厂AI课学习笔记】【1.6 人工智能基础知识】(3)神经网络
深度学习是机器学习中一种基于对数据进行表征学习的算法。观测值(例如一幅草莓照片)可以使用 多种方式来表示,如每个像素强度值的向量,或者更抽象地表示成一系列边、特定形状的区域等。 深度学习的最主要特征是使用神经网络作为计算模型。神经网络模型 …...
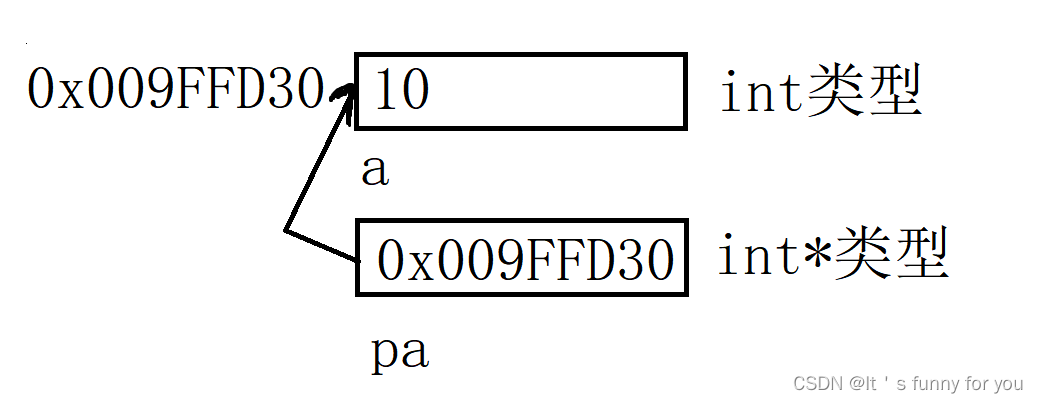
指针的基本含义及其用法
1.前言 在学习C语言的时候,我们会经常接触一个概念,指针和地址,关于这两个概念很多人并不能理解地十分透彻,接下来我将详细介绍一下这两者的概念 2.地址 我们知道计算机的上CPU(中央处理器)在处理数据的时…...

黄金交易策略(Nerve Nnife.mql4):趋势做单
完整EA:Nerve Knife.ex4黄金交易策略_黄金趋势ea-CSDN博客 当大小趋势相同行情走向也相同,就会开仓做顺势单,并会顺势追单,以达到快速止盈平仓的效果。大趋势追求稳定,小趋势追求敏捷,行情走向比小趋势更敏…...
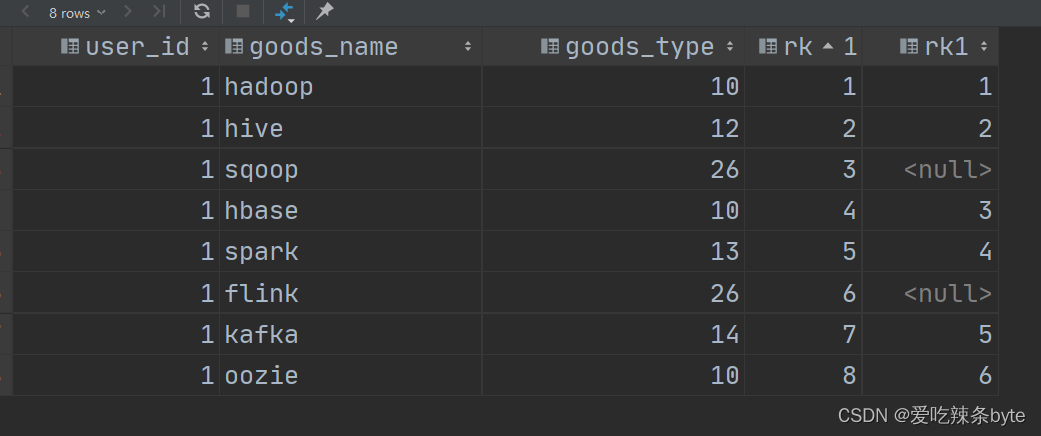
HiveSQL——条件判断语句嵌套windows子句的应用
注:参考文章: SQL条件判断语句嵌套window子句的应用【易错点】--HiveSql面试题25_sql剁成嵌套判断-CSDN博客文章浏览阅读920次,点赞4次,收藏4次。0 需求分析需求:表如下user_idgood_namegoods_typerk1hadoop1011hive1…...

ClickHouse--01--简介
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1. ClickHouse 简介官网: [https://clickhouse.com/docs/zh](https://clickhouse.com/docs/zh) 1.1 大数据处理场景1.2 什么是 ClickHouse1.3 OLAP 场景…...

【Django-ninja】在django ninja中处理异常
1. 直接抛内置异常 Django ninja内置了一些常用异常类。 from ninja.errors import HttpErrorapi.get("/some/resource") def some_operation(request):if True:raise HttpError(503, "Service Unavailable. Please retry later.")2. 覆写异常类 可以覆…...
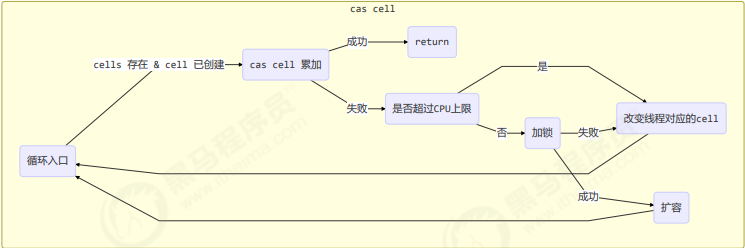
【并发编程】原子累加器
📝个人主页:五敷有你 🔥系列专栏:并发编程 ⛺️稳重求进,晒太阳 JDK8之后有专门做累加的类,效率比自己做快数倍以上 累加器性能比较 参数是方法 // supplier 提供者 无中生有 ()->结果// func…...
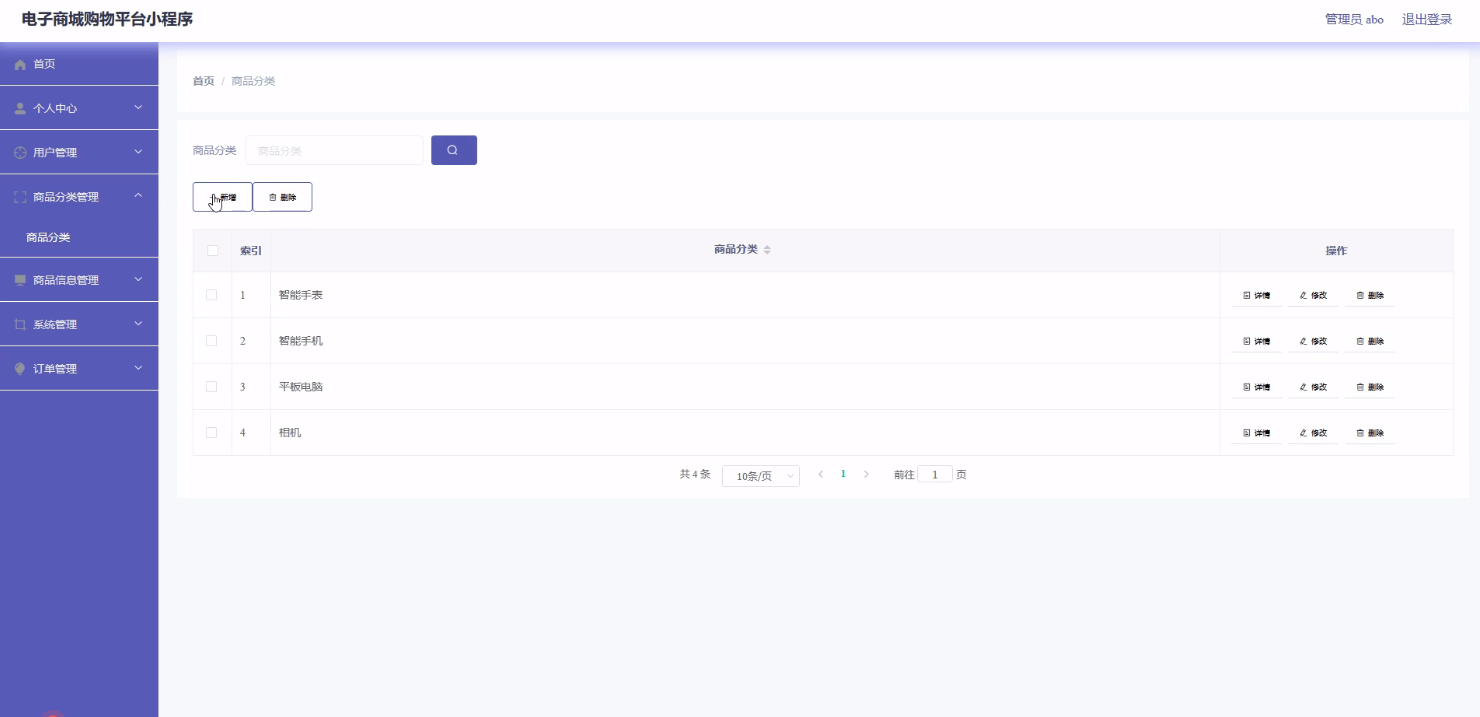
Java 基于微信小程序的电子商城购物系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

Git Push -f 命令详解
直接看原文: Git Push -f 命令详解 - 玩转Linux - SegmentFault 思否 -------------------------------------------------------------------------------------------------------------------------------- git push -f 这个命令的作用是将自己本地仓库的代码直接推送至仓…...

【LeetCode每日一题】前缀和的例题1248. 统计「优美子数组」974. 和可被 K 整除的子数组
leetcode 724. 寻找数组的中心索引 题目描述 给定一个整数类型的数组 nums,请编写一个能够返回数组 “中心索引” 的方法。 我们是这样定义数组 中心索引 的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。 如果数组不存在中心索引&…...

备战蓝桥杯---数学基础3
本专题主要围绕同余来讲: 下面介绍一下基本概念与定理: 下面给出解这方程的一个例子: 下面是用代码实现扩展欧几里得算法: #include<bits/stdc.h> using namespace std; int gcd(int a,int b,int &x,int &y){if(b…...

[算法学习] 逆元与欧拉降幂
费马小定理 两个条件: p为质数a与p互质 逆元 如果要求 x^-1 mod p ,用快速幂求 qmi(x,p-2) 就好 欧拉函数 思路:找到因数 i,phi / i * (i-1),除干净,判断最后的n 欧拉降幂 欧拉定理 应用示例 m! 是一个…...
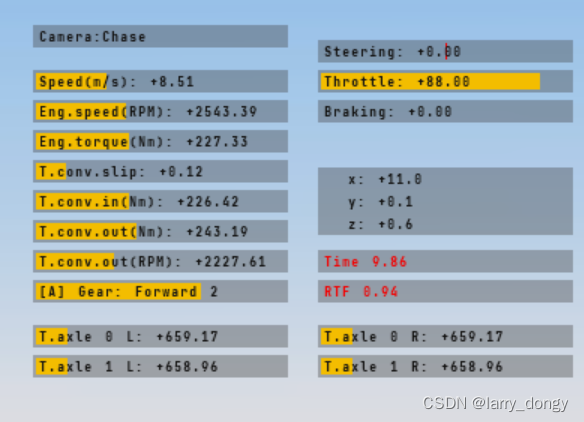
【Chrono Engine学习总结】4-vehicle-4.1-vehicle的基本概念
由于Chrono的官方教程在一些细节方面解释的并不清楚,自己做了一些尝试,做学习总结。 1、基本介绍 Vehicle Overview Vehicle Mannel Vehicle的官方demo 1.1 Vehicle的构型 一个车辆由许多子系统构成:悬挂、转向、轮子/履带、刹车/油门、动…...
腾讯云4核8G服务器多少钱?2024精准报价
腾讯云4核8G服务器S5和轻量应用服务器优惠价格表,轻量应用服务器和CVM云服务器均有活动,云服务器CVM标准型S5实例4核8G配置价格15个月1437.3元,5年6490.44元,标准型SA2服务器1444.8元一年,轻量应用服务器4核8G12M带宽一…...
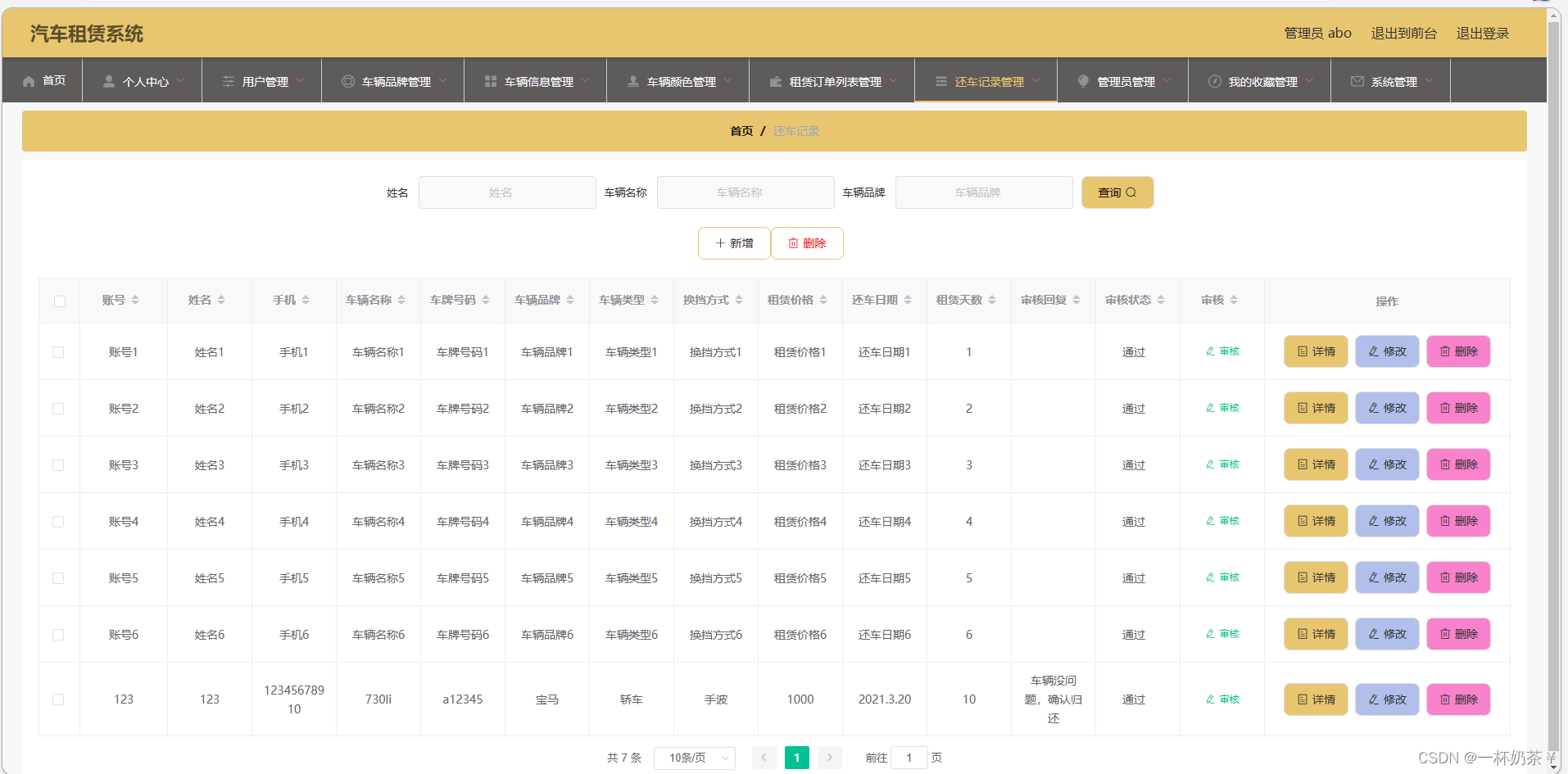
汽车出租管理系统
文章目录 汽车出租管理系统一、系统演示二、项目介绍三、系统部分功能截图四、部分代码展示五、底部获取项目源码(9.9¥带走) 汽车出租管理系统 一、系统演示 汽车租赁系统 二、项目介绍 语言:java 框架:SpringBoot、…...

使用SM4国密加密算法对Spring Boot项目数据库连接信息以及yaml文件配置属性进行加密配置(读取时自动解密)
一、前言 在业务系统开发过程中,我们必不可少的会使用数据库,在应用开发过程中,数据库连接信息往往都是以明文的方式配置到yaml配置文件中的,这样有密码泄露的风险,那么有没有什么方式可以避免呢?方案当然是有的,就是对数据库密码配置的时候进行加密,然后读取的时候再…...
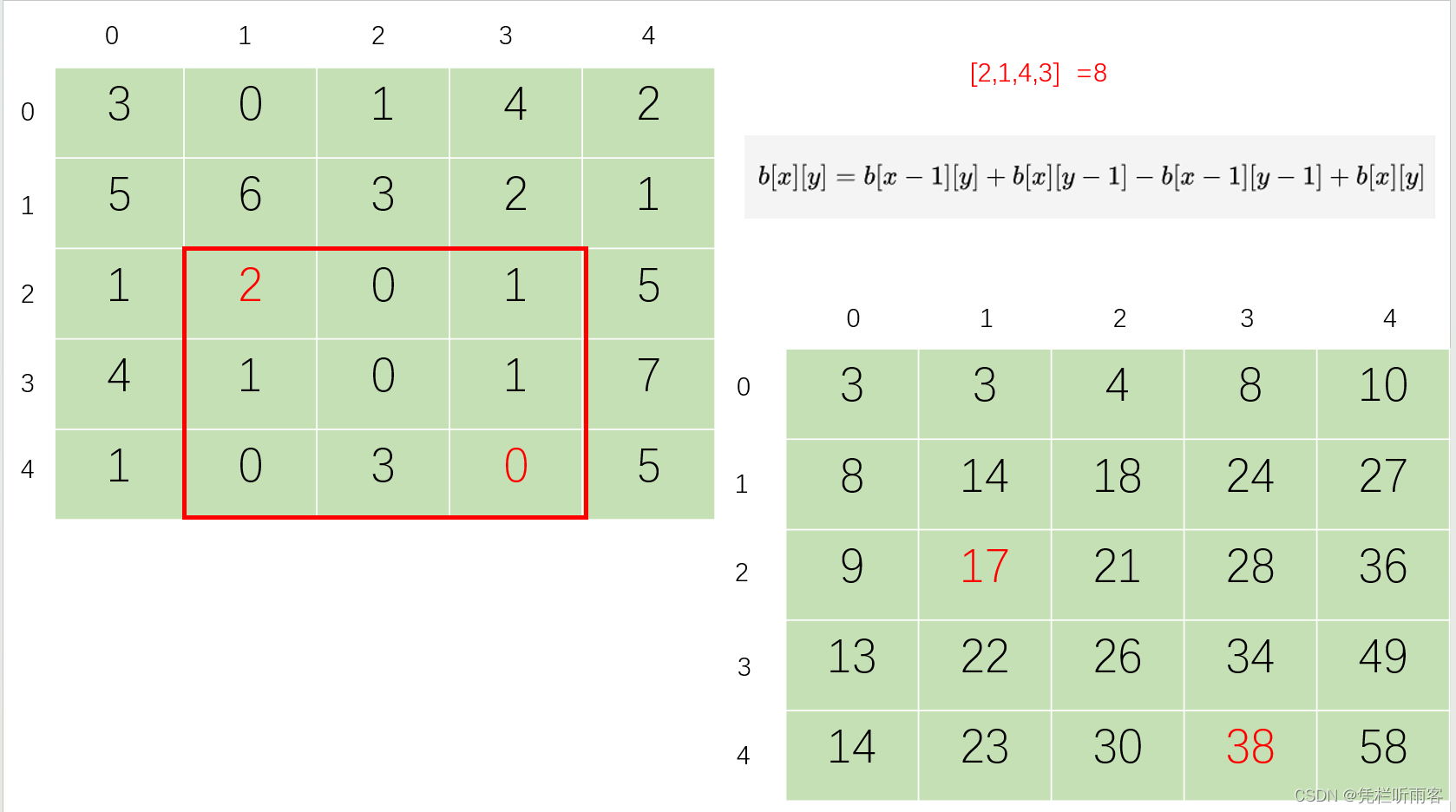
【LeetCode每日一题】二维前缀和基本概念与案例
二维前缀和 根据某个块块 的 左上角坐标,和右下角坐标 求出 块块的累加和。 304. 二维区域和检索 - 矩阵不可变 /*** param {number[][]} matrix*/ var NumMatrix function(matrix) {let row matrix.length;let col matrix[0].length;// 初始化一个二维数组&am…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...
