【LeetCode每日一题】前缀和的例题1248. 统计「优美子数组」974. 和可被 K 整除的子数组
leetcode 724. 寻找数组的中心索引
题目描述
给定一个整数类型的数组 nums,请编写一个能够返回数组 “中心索引” 的方法。
我们是这样定义数组 中心索引 的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。
如果数组不存在中心索引,那么我们应该返回 -1。如果数组有多个中心索引,那么我们应该返回最靠近左边的那一个。
/*** @param {number[]} nums* @return {number}*/
var pivotIndex = function(nums) {let sum = nums.reduce((a, b) => a + b, 0);let leftSum = 0;for(let i = 0; i < nums.length; i++){if(leftSum === sum - leftSum-nums[i]){return i;}leftSum+=nums[i];}return -1
};
560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
思路:
用map存放前缀和出现的位置,用一个count 维护出现的次数。
/*** @param {number[]} nums* @param {number} k* @return {number}*/
var subarraySum = function(nums, k) {let res = 0;let map = new Map();map.set(0, 1);let prefixSum = 0;for(let i = 0; i < nums.length; i++){prefixSum += nums[i];if(map.has(prefixSum - k)){res += map.get(prefixSum - k);}if(map.has(prefixSum)){map.set(prefixSum, map.get(prefixSum) + 1);}else{map.set(prefixSum, 1);}}return res;
};
930. 和相同的二元子数组
给你一个二元数组 nums ,nums[i] 不是 0 就是 1,和一个整数 goal ,请你统计并返回有多少个和为 goal 的 非空 子数组。
子数组 是数组的一段连续部分。
示例 1:
输入:nums = [1,0,1,0,1], goal = 2
输出:4
解释:
有 4 个满足题目要求的子数组:[1,0,1]、[1,0,1,0]、[0,1,0,1]、[1,0,1]示例 2:
输入:nums = [0,0,0,0,0], goal = 0
输出:15
/*** @param {number[]} nums* @param {number} goal* @return {number}*/
var numSubarraysWithSum = function(nums, goal) {let map = new Map();map.set(0, 1);let res = 0;let prefixSum = 0;for(let i = 0; i < nums.length; i++){prefixSum += nums[i];if(map.has(prefixSum - goal)){res += map.get(prefixSum - goal);}if(map.has(prefixSum)){map.set(prefixSum, map.get(prefixSum) + 1);}else{map.set(prefixSum, 1);}}return res;
};
leetcode1248. 统计「优美子数组」
给你一个整数数组 nums 和一个整数 k。如果某个连续子数组中恰好有 k 个奇数数字,我们就认为这个子数组是「优美子数组」。
请返回这个数组中 「优美子数组」 的数目。
思路:简化数组 + 930. 和相同的二元子数组
var numberOfSubarrays = function(nums, k) {// 简化数组nums = nums.map(item=>item%2===0?0:1)let res = 0;let map = new Map();map.set(0, 1);let prefixSum = 0;for(let i = 0; i < nums.length; i++){prefixSum += nums[i];if(map.has(prefixSum - k)){res += map.get(prefixSum - k);}if(map.has(prefixSum)){map.set(prefixSum, map.get(prefixSum) + 1);}else{map.set(prefixSum, 1);}}return res;
};
974. 和可被 K 整除的子数组
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目。
思路:
x - y 能够被 k 整除,
⇒ (x - y)% k = 0
⇒ x % k - y % k = 0
⇒ x % k = y % k
用map存储presum % k 的结果,如果有相同的 ,则说明 x - y 能够被 k 整除
/*** @param {number[]} nums* @param {number} k* @return {number}*/
var subarraysDivByK = function(nums, k) {let res = 0;let map = new Map();map.set(0, 1);let prefixSum = 0 ;for(let i = 0; i < nums.length; i++){prefixSum += nums[i];let key = (prefixSum % k + k) % k; //如果是负数,需要 + k 修正,如果+k 后大于k,需要%k。if(map.has(key)){res += map.get(key);map.set(key, map.get(key) + 1);}else{map.set(key, 1);}}return res;
};
523. 连续的子数组和
给你一个整数数组 nums 和一个整数 k ,编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组:
- 子数组大小 至少为 2 ,且
- 子数组元素总和为
k的倍数。
如果存在,返回 true ;否则,返回 false 。
如果存在一个整数 n ,令整数 x 符合 x = n * k ,则称 x 是 k 的一个倍数。0 始终视为 k 的一个倍数。
思路:
map :key 存放preSum,value存放第一次出现的索引。只要最长的大于等于2 ,即为存在。
/*** @param {number[]} nums* @param {number} k* @return {boolean}*/
var checkSubarraySum = function(nums, k) {let map = new Map();map.set(0, -1);let prefixSum = 0;for(let i = 0; i < nums.length; i++){prefixSum += nums[i];let key = (prefixSum % k+k)%k;if(map.has(key)){if(i - map.get(key) >= 2){return true;}}else{map.set(key, i);}}return false;
};
相关文章:

【LeetCode每日一题】前缀和的例题1248. 统计「优美子数组」974. 和可被 K 整除的子数组
leetcode 724. 寻找数组的中心索引 题目描述 给定一个整数类型的数组 nums,请编写一个能够返回数组 “中心索引” 的方法。 我们是这样定义数组 中心索引 的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。 如果数组不存在中心索引&…...

备战蓝桥杯---数学基础3
本专题主要围绕同余来讲: 下面介绍一下基本概念与定理: 下面给出解这方程的一个例子: 下面是用代码实现扩展欧几里得算法: #include<bits/stdc.h> using namespace std; int gcd(int a,int b,int &x,int &y){if(b…...

[算法学习] 逆元与欧拉降幂
费马小定理 两个条件: p为质数a与p互质 逆元 如果要求 x^-1 mod p ,用快速幂求 qmi(x,p-2) 就好 欧拉函数 思路:找到因数 i,phi / i * (i-1),除干净,判断最后的n 欧拉降幂 欧拉定理 应用示例 m! 是一个…...
【Chrono Engine学习总结】4-vehicle-4.1-vehicle的基本概念
由于Chrono的官方教程在一些细节方面解释的并不清楚,自己做了一些尝试,做学习总结。 1、基本介绍 Vehicle Overview Vehicle Mannel Vehicle的官方demo 1.1 Vehicle的构型 一个车辆由许多子系统构成:悬挂、转向、轮子/履带、刹车/油门、动…...
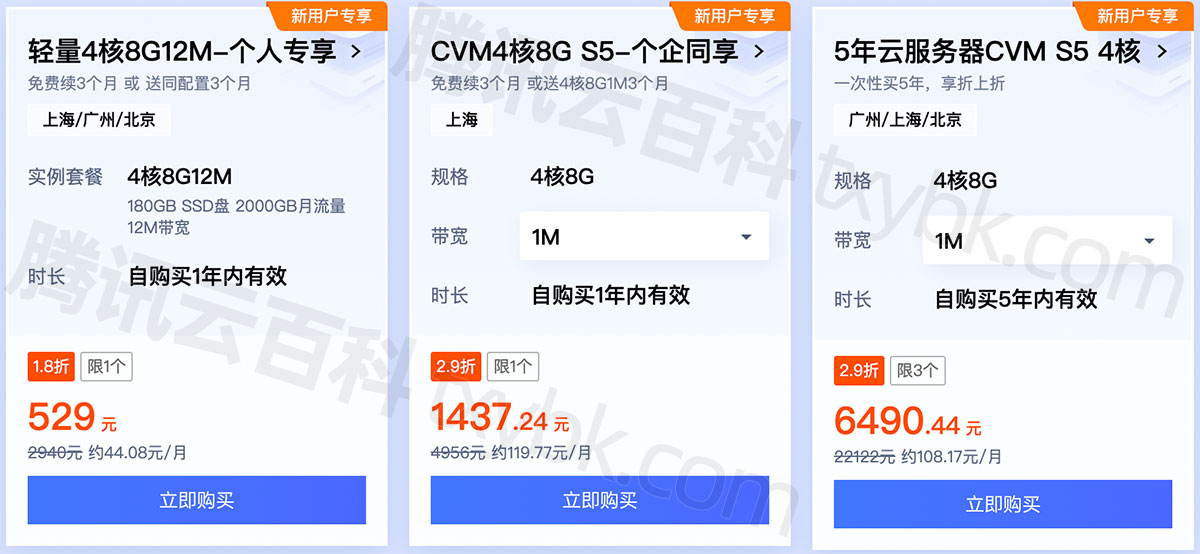
腾讯云4核8G服务器多少钱?2024精准报价
腾讯云4核8G服务器S5和轻量应用服务器优惠价格表,轻量应用服务器和CVM云服务器均有活动,云服务器CVM标准型S5实例4核8G配置价格15个月1437.3元,5年6490.44元,标准型SA2服务器1444.8元一年,轻量应用服务器4核8G12M带宽一…...
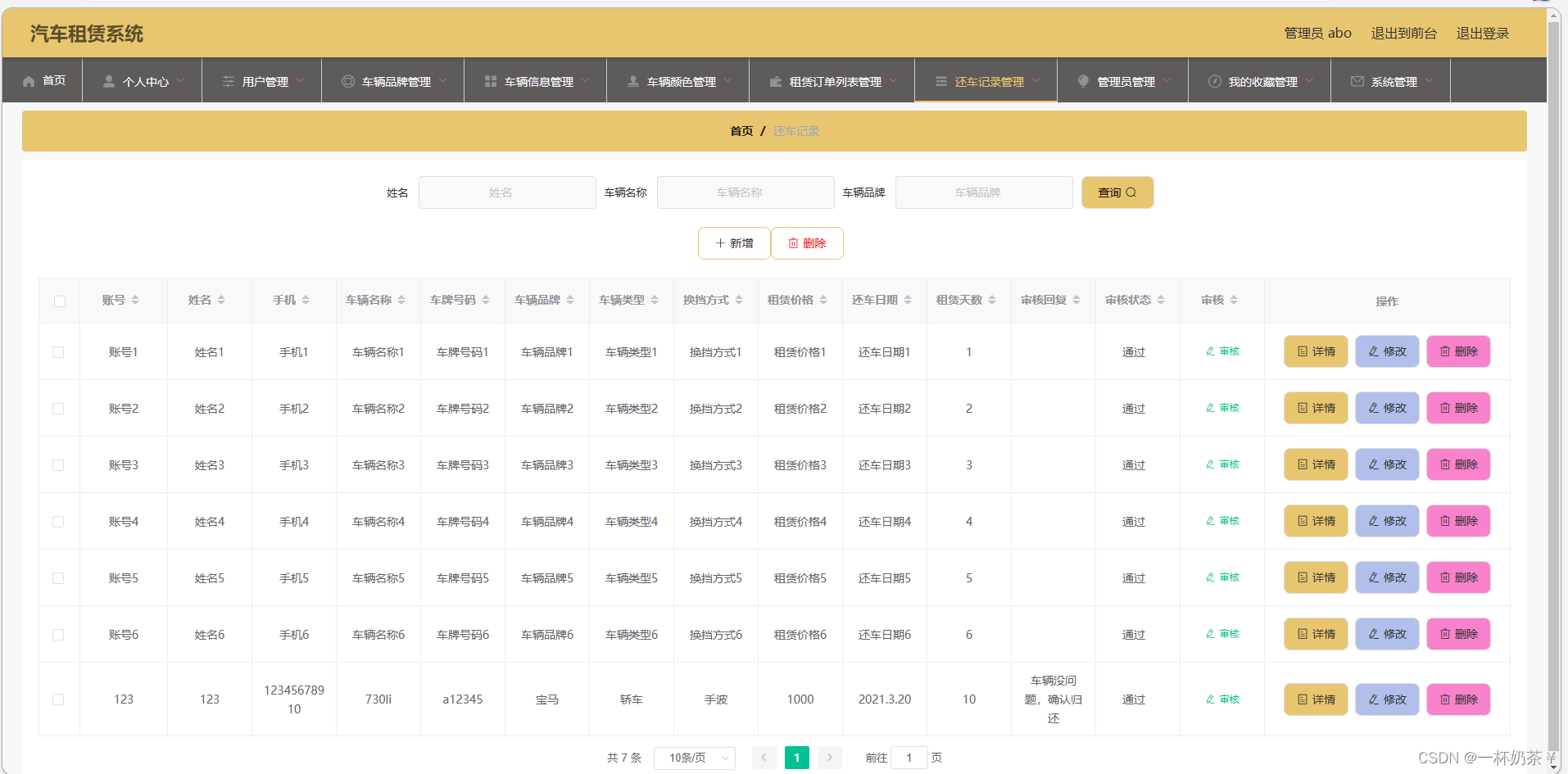
汽车出租管理系统
文章目录 汽车出租管理系统一、系统演示二、项目介绍三、系统部分功能截图四、部分代码展示五、底部获取项目源码(9.9¥带走) 汽车出租管理系统 一、系统演示 汽车租赁系统 二、项目介绍 语言:java 框架:SpringBoot、…...

使用SM4国密加密算法对Spring Boot项目数据库连接信息以及yaml文件配置属性进行加密配置(读取时自动解密)
一、前言 在业务系统开发过程中,我们必不可少的会使用数据库,在应用开发过程中,数据库连接信息往往都是以明文的方式配置到yaml配置文件中的,这样有密码泄露的风险,那么有没有什么方式可以避免呢?方案当然是有的,就是对数据库密码配置的时候进行加密,然后读取的时候再…...
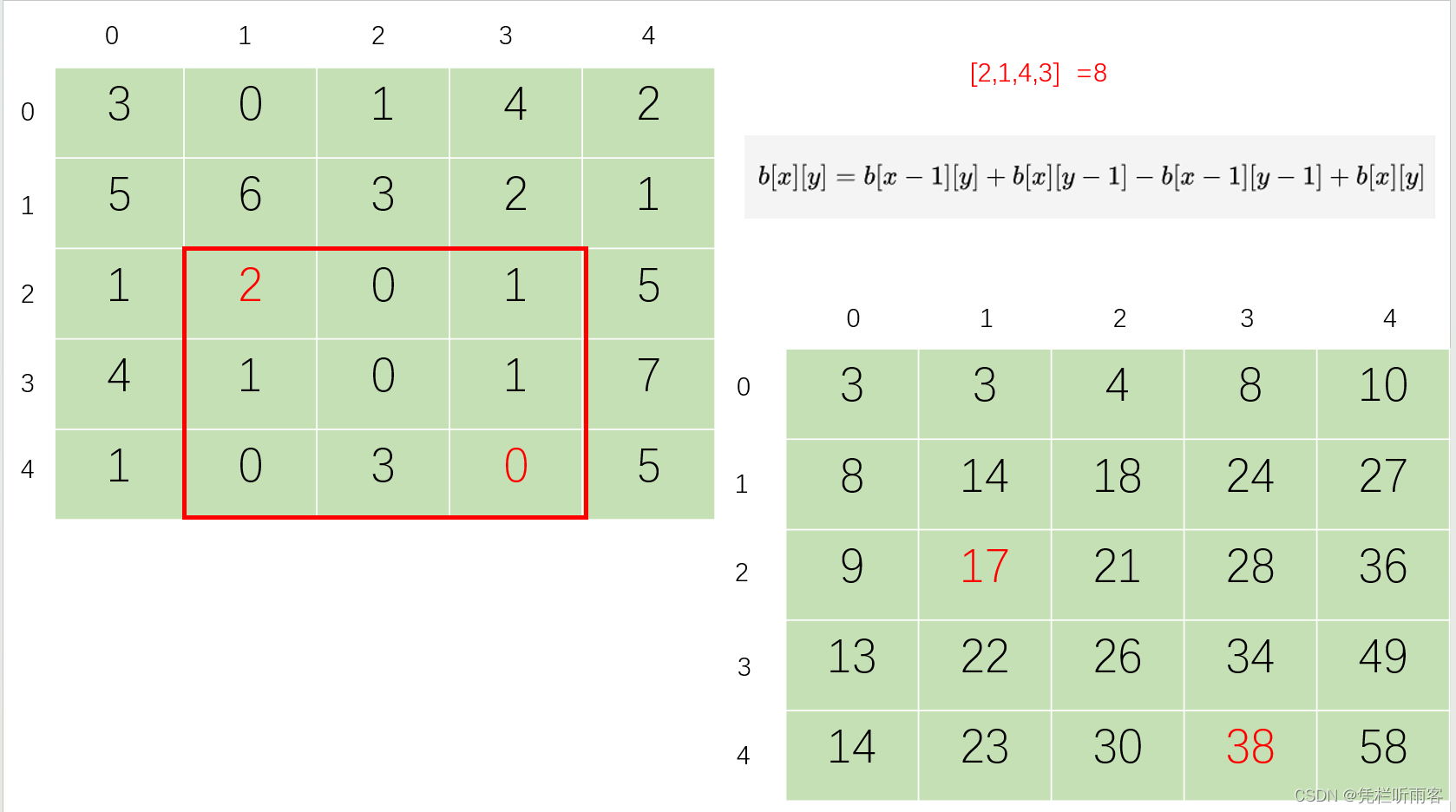
【LeetCode每日一题】二维前缀和基本概念与案例
二维前缀和 根据某个块块 的 左上角坐标,和右下角坐标 求出 块块的累加和。 304. 二维区域和检索 - 矩阵不可变 /*** param {number[][]} matrix*/ var NumMatrix function(matrix) {let row matrix.length;let col matrix[0].length;// 初始化一个二维数组&am…...
计算机网络——网络安全
计算机网络——网络安全 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家, [跳转到网站](https://www.captainbed.cn/qianqiu) 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU) 网络安全何…...

SQl 注入 - 利用报错函数updatexml及extracevalue
环境准备:构建完善的安全渗透测试环境:推荐工具、资源和下载链接_渗透测试靶机下载-CSDN博客 一、updatexml() 函数 1. 使用前提: 在 MySQL 高版本中(大于5.1版本)添加了对 XML 文档进行查询和修改的函数,包括 updatexml() 和 extractvalue()。 2. 显示错误处理: 在…...
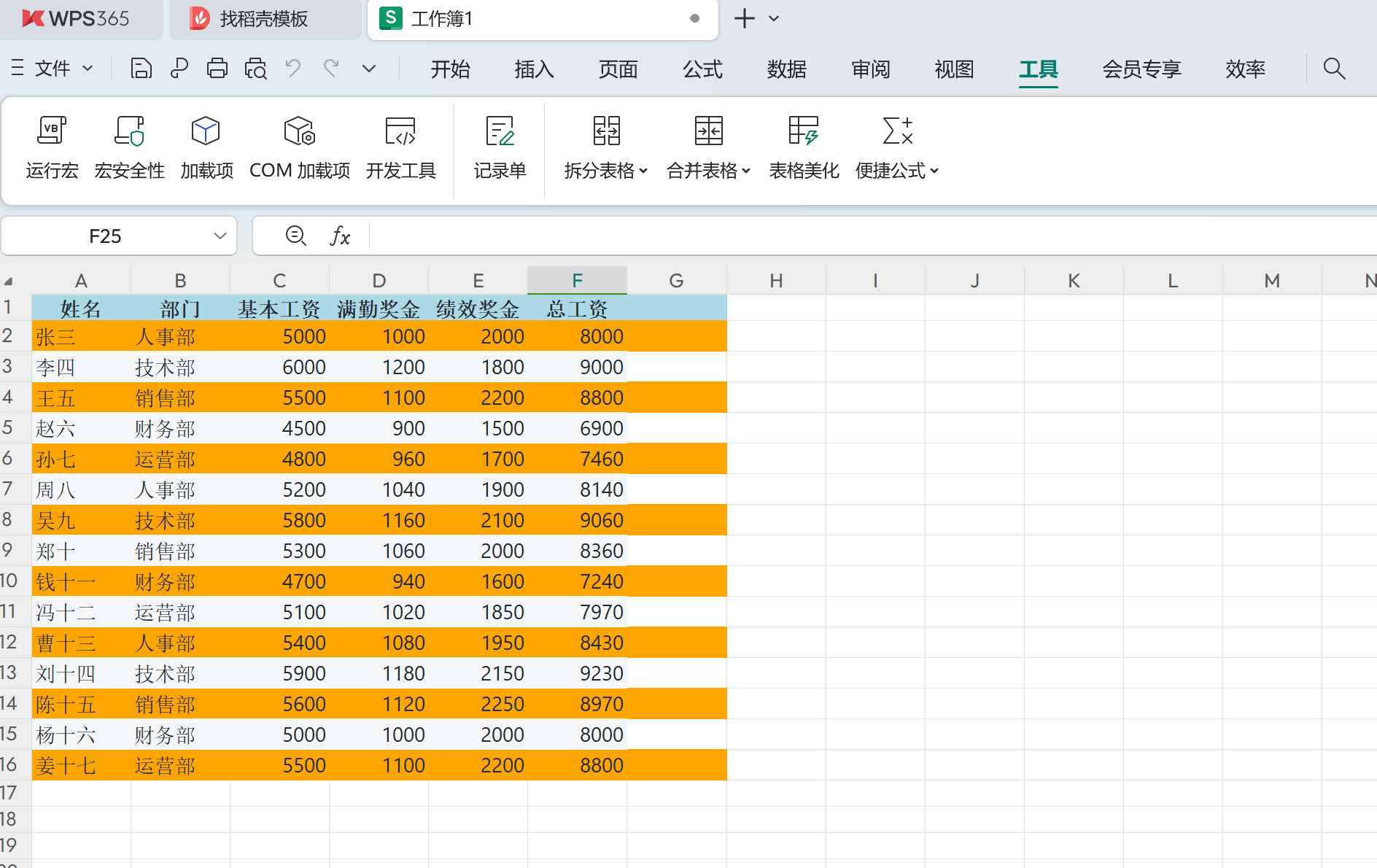
ChatGPT高效提问—prompt实践(生成VBA)
ChatGPT高效提问—prompt实践(生成VBA) 2. 生成VBA函数操作Excel 当前Excel表格数据无背景颜色,区分不明显。假如我们想美化数据展示效果,把标题行设置为浅蓝色,其余奇数行设置为橙色,该怎么操作呢?这次我们基于ChatGPT写一个prompt来创建VBA函数。 输入prompt…...

Ps:直接从图层生成文件(图像资源)
通过Ps菜单:文件/导出/将图层导出到文件 Layers to Files命令,我们可以快速地将当前文档中的每个图层导出为同一类型、相同大小和选项的独立文件。 Photoshop 还提供了一个功能,可以基于文档中的图层或图层组的名称,自动生成指定大…...

springboot-接入ai机器人 汇总
鱼聪明 Java SDKGitHub - liyupi/yucongming-java-sdk: 鱼聪明 AI 的 Java SDK,几行代码使用 AI 助手能力!...

蓝桥杯嵌入式第9届真题(完成) STM32G431
蓝桥杯嵌入式第9届真题(完成) STM32G431 题目 分析和代码 main.h /* USER CODE BEGIN Header */ /********************************************************************************* file : main.h* brief : Header for main.c file.* …...
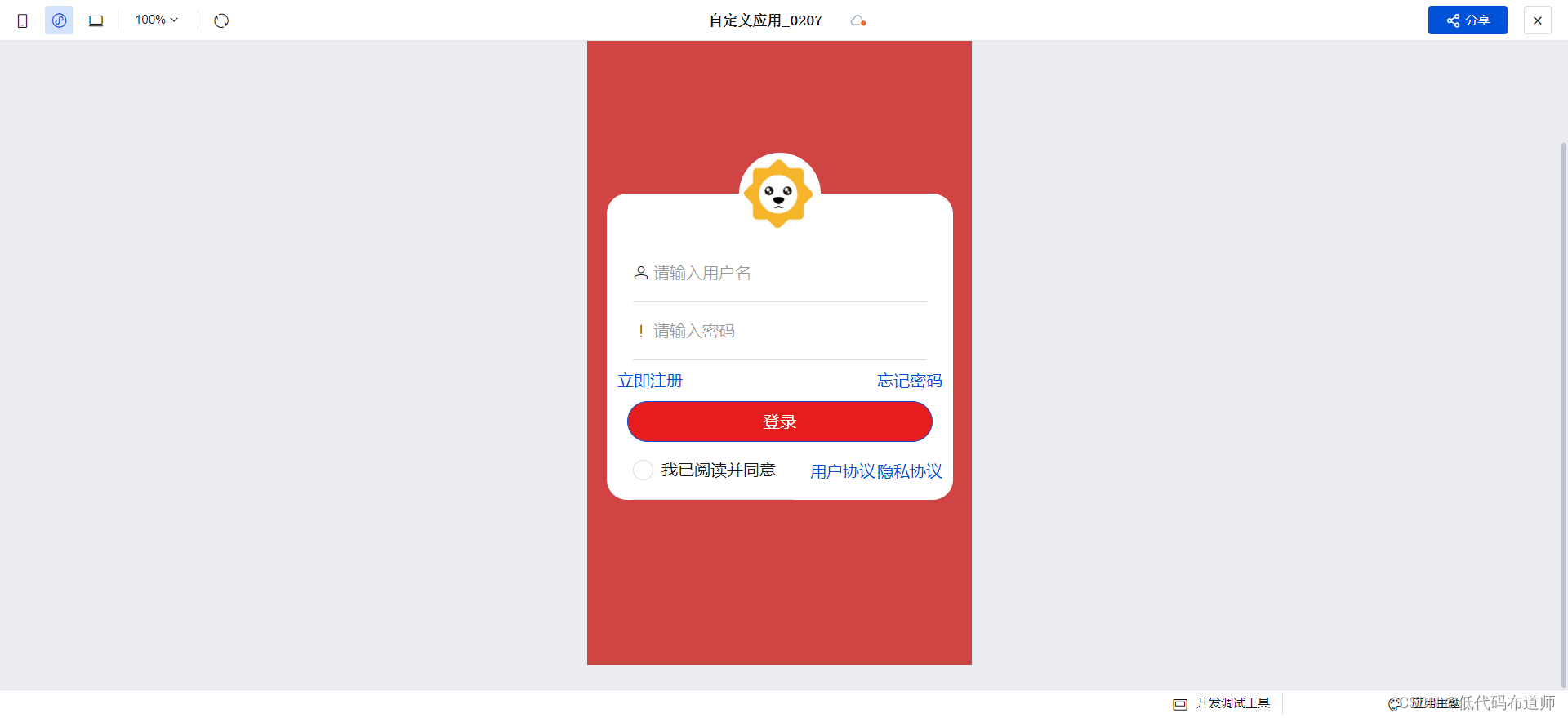
电商小程序03登录页面开发
目录 1 创建应用2 创建页面3 首页功能搭建4 登录页搭建5 设置叠加效果总结 小程序开发在经过需求分析和数据源设计之后,就可以进入到页面开发的阶段了。首先我们需要开发登录的功能。 登录功能要求用户输入用户名和密码,勾选同意用户协议和隐私协议&…...

聊聊PowerJob的CleanService
序 本文主要研究一下PowerJob的CleanService CleanService Slf4j Service public class CleanService {private final DFsService dFsService;private final InstanceInfoRepository instanceInfoRepository;private final WorkflowInstanceInfoRepository workflowInstance…...

Qt QML学习(一):Qt Quick 与 QML 简介
参考引用 QML和Qt Quick快速入门全面认识 Qt Widgets、QML、Qt Quick 1. Qt Widgets、QML、Qt Quick 区别 1.1 QML 和 Qt Quick 是什么关系? 1.1.1 从概念上区分 QML 是一种用户界面规范和标记语言,它允许开发人员创建高性能、流畅的动画和具有视觉吸引…...

Kylin系统下Qt的各种中文问题解决思路
一、编译生成的程序运行,中文乱码 这个比较简单。 Windows下基本就是编码格式设置。ini中文问题,见QSettings读取ini中文key方法。 其他Linux版本没玩过,不清楚。Kylin系统下基本就是缺中文的字库。找个好的中文字库,放到目录下即可,系统目录/usr/lib/fonts,qt的安装目…...

C 练习实例69-约瑟夫环
题目:有n个人围成一圈,顺序排号。从第一个人开始报数(从1到3报数),凡报到3的人退出圈子,问最后留下的是原来第几号的那位。 代码: #include <stdio.h> int main() {int n8;int table[n]…...
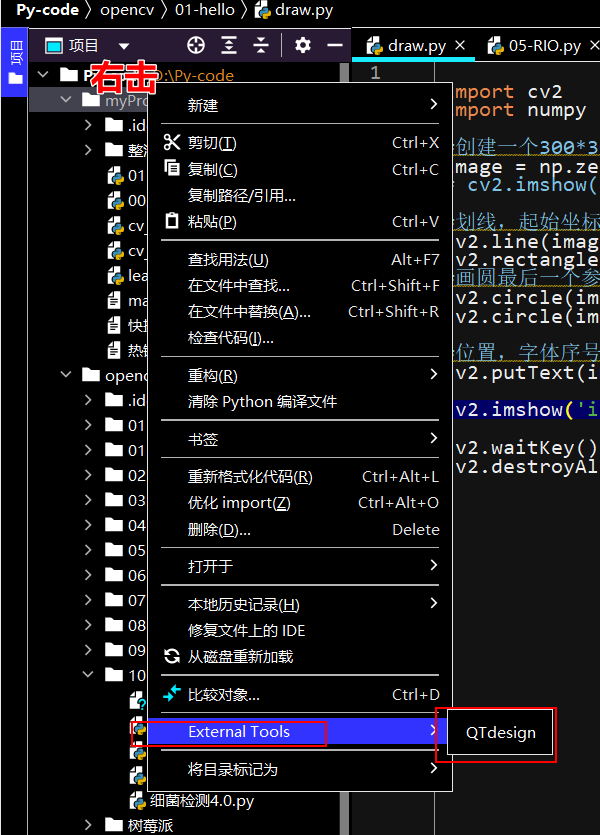
【Qt Design】界面介绍
文章目录 前言Widget Box(工具箱)对象查看器Qt Design属性编译器sizePolicy内容 信号/槽编辑器资源浏览器ui文件编辑完窗口后查看代码在Pycharm中添加QtDesign 前言 Widget Box(工具箱) 提供很多控件 对象查看器 对象查看区域…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
