C++ 堆排序
C++ 堆排序
堆排序是一种基于二叉堆数据结构的排序算法,其原理如下:
构建最大堆:将待排序的数组看作一个完全二叉树,并通过调整节点的位置构建一个最大堆。最大堆满足每个父节点的值都大于或等于其子节点的值。构建最大堆的过程可以从最后一个非叶子节点开始,逐步向前,对每个节点进行下沉操作,使得子树满足最大堆的性质。
排序过程:构建完成最大堆后,将堆顶元素(即最大值)与数组的最后一个元素交换。然后,将堆的大小减1,再对堆顶元素执行下沉操作,以重新满足最大堆的性质。重复这个过程,直到堆的大小减少到1。最终,得到的数组就是有序的。
堆排序的关键操作是下沉(sink)和上浮(swim):
- 下沉操作:将某个节点与其子节点中较大的节点交换位置,并递归地对交换后的子节点执行下沉操作,直到满足最大堆的性质。
- 上浮操作:将某个节点与其父节点比较,如果节点的值大于父节点的值,则交换位置,并递归地对交换后的父节点执行上浮操作,直到满足最大堆的性质。
堆排序的时间复杂度为O(n log n),其中n是待排序数组的长度。构建最大堆的时间复杂度是O(n),排序过程需要进行n次下沉操作,每次下沉操作的时间复杂度是O(log n)。由于堆排序是原地排序算法,不需要额外的辅助空间,因此空间复杂度是O(1)。
需要注意的是,堆排序是不稳定的排序算法,即相等元素的相对顺序可能会发生改变。
#include <iostream>
using namespace std;void heapify(int arr[], int n, int i) {int largest = i; // 将当前节点设置为最大值int left = 2 * i + 1; // 左子节点索引int right = 2 * i + 2; // 右子节点索引// 如果左子节点存在且大于根节点,则更新最大值索引if (left < n && arr[i] < arr[left]) {largest = left;}// 如果右子节点存在且大于根节点或左子节点,则更新最大值索引if (right < n && arr[largest] < arr[right]) {largest = right;}// 如果最大值不是根节点,则交换根节点和最大值,并继续调整堆if (largest != i) {swap(arr[i], arr[largest]);heapify(arr, n, largest);}
}void heapSort(int arr[], int n) {// 构建最大堆(从最后一个非叶子节点开始)for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}// 逐个将最大值移到数组末尾,并重新调整堆for (int i = n - 1; i > 0; i--) {swap(arr[0], arr[i]); // 交换根节点和最后一个节点heapify(arr, i, 0);}
}int main() {int arr[] = {12, 11, 13, 5, 6, 7};int n = sizeof(arr) / sizeof(arr[0]);heapSort(arr, n);cout << "排序后的数组: ";for (int i = 0; i < n; i++) {cout << arr[i] << " ";}return 0;
}
相关文章:

C++ 堆排序
C 堆排序 堆排序是一种基于二叉堆数据结构的排序算法,其原理如下: 构建最大堆:将待排序的数组看作一个完全二叉树,并通过调整节点的位置构建一个最大堆。最大堆满足每个父节点的值都大于或等于其子节点的值。构建最大堆的过程可以…...
U3D记录之FBX纹理丢失问题
今天费老大劲从blender建了个模型,然后导出进去unity 发现贴图丢失 上网查了一下 首先blender导出要改设置 这个path mode要copy 然后unity加载纹理也要改设置 这里这个模型的纹理load要改成external那个模式 然后就有了,另外这个导出还有好多选项可…...

监测Nginx访问日志502情况后并做相应动作
今天带大家写一个比较实用的脚本哈 原理: 假设服务器环境为lnmp,近期访问经常出现502现象,且502错误在重启php-fpm服务后消失,因此需要编写监控脚本,一旦出现502,则自动重启php-fpm服务 场景: 1…...

【数据分享】1929-2023年全球站点的逐年平均风速(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、能见度等指标,说到气象数据,最详细的气象数据是具体到气象监测站点的数据! 有关气象指标的监测站点数据,之前我们分享过1929-2023年全球气象站…...

Android性能调优 - 应用安全问题
Android应用安全 1.组件暴露: 像比如ContentProvider,BroadcastReceiver,Activity等组件有android:exported属性; 如果是私有组件 android:exported “false”; 如果是公有组件 android:exported “true” 且进行权限控制&…...
等常见的方法)
C#的Char 结构的像IsLetterOrDigit(Char)等常见的方法
目录 一、Char 结构的方法 二、Char.IsLetterOrDigit 方法 1.Char.IsLetterOrDigit(Char)用法 2.IsLetterOrDigit(String, Int32)方法 三、Char.IsLetter 方法 1.IsLetter(Char) 2.IsLetter(String, Int32) 四、Char.IsDigit 方法 1. IsDigit(String, Int32) 2.IsDig…...
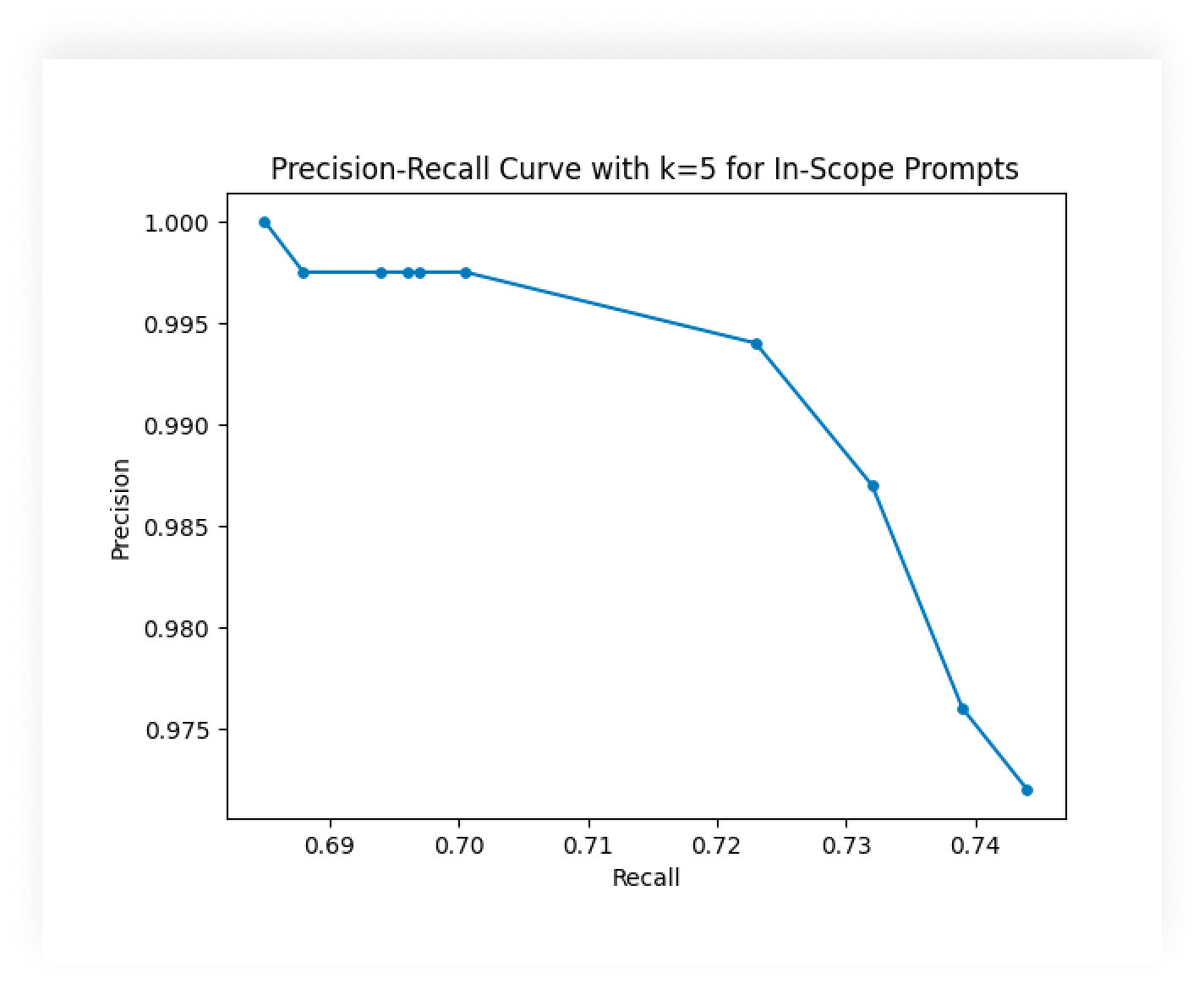
部分意图分类【LLM+RAG】
在生成人工智能领域工作最有价值的事情之一就是发现新兴技术如何融入新的解决方案。 举个例子:在为北美顶级金融服务公司之一设计对话式人工智能助手时,WillowTree 的数据和人工智能研究团队 (DART) 发现,将意图分类与大型语言模型 (LLM) 结合…...

1277. 统计全为 1 的正方形子矩阵
1277. 统计全为 1 的正方形子矩阵 题目链接:1277. 统计全为 1 的正方形子矩阵 代码如下: class Solution { public:int countSquares(vector<vector<int>>& matrix) {if(matrix.size()0||matrix[0].size()0) return 0;//dp[i][j]代表…...

Python 3 时间序列可视化指南
简介 时间序列分析属于统计学的一个分支,涉及对有序的、通常是时间性的数据进行研究。当适当应用时,时间序列分析可以揭示意想不到的趋势,提取有用的统计数据,甚至预测未来的趋势。因此,它被应用于许多领域࿰…...

[算法前沿]--059-大语言模型Fine-tuning踩坑经验之谈
前言 由于 ChatGPT 和 GPT4 兴起,如何让人人都用上这种大模型,是目前 AI 领域最活跃的事情。当下开源的 LLM(Large language model)非常多,可谓是百模大战。面对诸多开源本地模型,根据自己的需求,选择适合自己的基座模型和参数量很重要。选择完后需要对训练数据进行预处…...

【Docker】01 Docker安装与配置
文章目录 一、Docker二、离线安装Docker三、联网安装Docker3.1 下载YUM软件库文件3.2 安装epel-release3.3 安装yum-utils3.4 设置镜像仓库3.5 查看docker-ce所有版本3.6 安装Docker3.7 启动Docker3.8 查看Docker信息3.9 启动第一个容器 四、一些配置4.1 登录DockerHub4.2 镜像…...

Unity3d Shader篇(六)— BlinnPhong高光反射着色器
文章目录 前言一、BlinnPhong高光反射着色器是什么?1. BlinnPhong高光反射着色器的工作原理2. BlinnPhong高光反射着色器的优缺点优点缺点 3. 公式 二、使用步骤1. Shader 属性定义2. SubShader 设置3. 渲染 Pass4. 定义结构体和顶点着色器函数5. 片元着色器函数 三…...
定时任务的选择调研)
Go-zero微服务个人探究之路(十二)定时任务的选择调研
前言 很多时候后台需要做定时任务的需求,笔者的项目采用go-zero框架微服务框架,需要做定时任务,于是做了如下方法调研,共有大概三种主要选择 方案 难度总体由容易到复杂 go的timer库 通过Go的标准库time中的Ticker和Tick功能…...

Java中,List、Map和Set的区别是什么?
在Java中,List、Map和Set是三种常用的集合类型,它们之间的主要区别如下: 1、List List是有序集合,它可以包含重复元素。 List中的元素是按照插入顺序排列的,可以通过索引访问每个元素。 Java中常见的List实现类有A…...
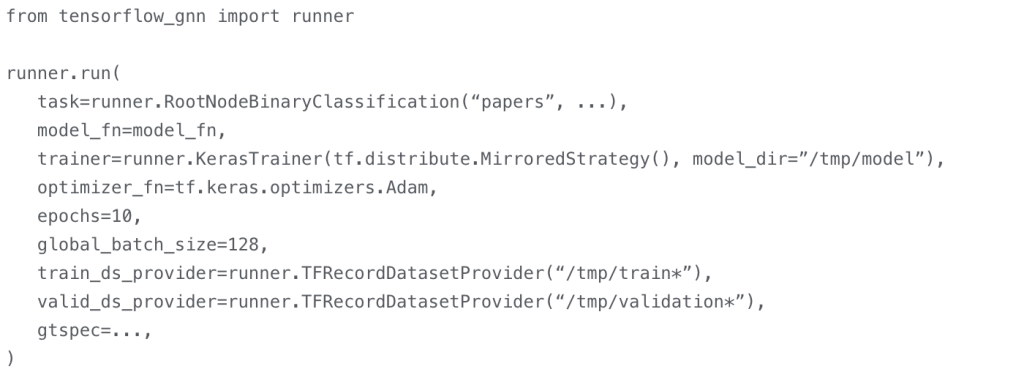
Google刚刚推出了图神经网络Tensorflow-GNN
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
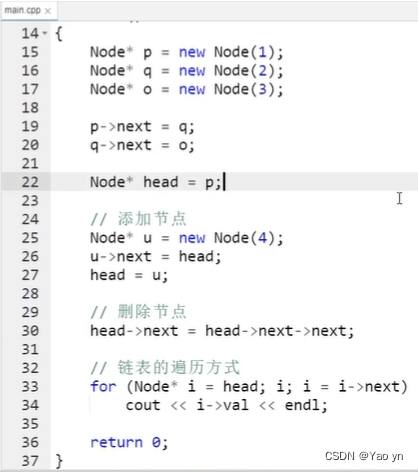
链表基础知识汇总
链表 链表是一种基本的数据结构,是由一系列节点组成的集合。每个节点包含两个部分:值和指向下一个节点的指针。链表中的节点可以动态地添加、删除,其大小可以根据需要进行扩展或缩小。 链表通常用于处理不固定长度的数据结构,具有…...
)
Educational Codeforces Round 2(远古edu计划)
A. 恶心模拟。。 模拟一下分类即可 数字类,数字0,或者都是数字 字母类,字母空的也是字母,有字母就是字母 #include<bits/stdc.h> #define INF 1e9 using namespace std; typedef long long ll; const int N2e59; strin…...
【Tauri】(1):使用Tauri1.5版本,进行桌面应用开发,在windows,linux进行桌面GUI应用程序开发,可以打包成功,使用 vite 最方便
1,视频地址: https://www.bilibili.com/video/BV1Pz421d7s4/ 【Tauri】(1):使用Tauri1.5版本,进行桌面应用开发,在windows,linux进行桌面GUI应用程序开发,可以打包成功&…...

「Linux」软件安装
MySQL5.7在CentOS安装 安装 配置yum仓库 更新密钥:rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysql-2022安装MySQL yum库:rpm -Uvh http://repo.mysql.com//mysql57-community-release-el7-7.noarch.rpm使用yum安装MySQL:yum -y in…...

Ubuntu Desktop - Terminal 输出全部选中 + 复制
Ubuntu Desktop - Terminal 输出全部选中 复制 1. Terminal2. Terminal 最大化3. Edit -> Select All4. Copy & PasteReferences 1. Terminal 2. Terminal 最大化 3. Edit -> Select All 4. Copy & Paste Edit -> Copy or Shift Ctrl C Edit -> Paste…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
