剑指offer——旋转数组的最小数字
目录
- 1. 题目描述
- 2. 分析思路
- 2.1 示例分析
- 3. 更完美的做法
1. 题目描述
- 把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3.4,5,1.2}为{1.2,3,4,5}的一个旋转,该数组的最小值为 1。
2. 分析思路
- 这道题最直观的解法并不难,从头到尾遍历数组一次,我们就能找出最小的元素。
- 这种思路的时间复杂度显然是O(n)。但是这个思路没有利用输入的旋转数组的特性,肯定达不到面试官的要求。
- 我们注意到旋转之后的数组实际上可以划分为两个排序的子数组,而且前面的子数组的元素都大于或者等于后面子数组的元素。
- 我们还注意到最小的元素刚好是这两个子数组的分界线。
- 在排序的数组中我们可以用二分查找法实现 O(logn)的查找。
- 本题给出的数组在一定程度上是排序的,因此我们可以试着用二分查找法的思路来寻找这个最小的元素。
- 和二分查找法一样,我们用两个指针分别指向数组的第一个元素和最后一个元素。
- 按照题目中旋转的规则,第一个元素应该是大于或者等于最后一个元素的(这其实不完全对,还有特例,后面再加以讨论)。
- 接着我们可以找到数组中间的元素。
- 如果该中间元素位于前面的递增子数组,那么它应该大于或者等于第一个指针指向的元素。
- 此时数组中最小的元素应该位于该中间元素的后面。
- 我们可以把第一个指针指向该中间元素,这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组之中。
- 同样,如果中间元素位于后面的递增子数组,那么它应该小于或者等于第二个指针指向的元素。
- 此时该数组中最小的元素应该位于该中间元素的前面。
- 我们可以把第二个指针指向该中间元素,这样也可以缩小寻找的范围。
- 移动之后的第二个指针仍然位于后面的递增子数组之中。
- 不管是移动第一个指针还是第二个指针,查找范围都会缩小到原来的一半。接下来我们再用更新之后的两个指针,重复做新一轮的查找
- 按照上述的思路,第一个指针总是指向前面递增数组的元素,而第一个指针总是指向后面递增数组的元素。
- 最终第一个指针将指向前面子数组的最后一个元素,而第二个指针会指向后面子数组的第一个元素。
- 也就是它们最终会指向两个相邻的元素,而第二个指针指向的刚好是最小的元素。这就是循环结束的条件。
2.1 示例分析
- 以前面的数组{3.4,5.1.2}为例,我们先把第一个指针指向第0个元素,把第二个指针指向第4个元素(如图2.10(a)所示)。
- 位于两个指针中间(在数组中的下标是2)的数字是5,它大于第一个指针指向的数字。
- 因此中间数字5一定位于第一个递增子数组中,并且最小的数字一定位于它的后面。
- 因此我们可以移动第一个指针让它指向数组的中间(图2.10(b)所示)。
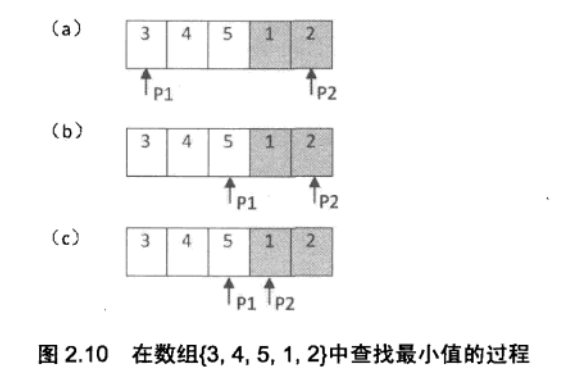
- 注:旋转数组中包含两个递增排序的子数组,有阴影背景的是第二个子数组。(a)把P1指向数组的第一个数字,P2指向数组的最后一个数字。由于P1和P2中间的数字5大于P1指向的数字,中间的数字在第一个子数组中。下一步把P1指向中间的数字。(b)P1和P2中间的数字1小于 P2指向的数字,中间的数字在第二个子数组中。下一步把P2指向中间的数字。©P1和P2指向两个相邻的数字,则P2指向的是数组中的最小数字。
- 此时两个指针的距离是1,表明第一个指针已经指向了第一个递增子数组的末尾,而第二个指针指向第二个递增子数组的开头。
- 第二个子数组的第一个数字就是最小的数字,因此第二个指针指向的数字就是我们查找的结果。
- 基于这个思路我们可以写出如下代码:
#define ROW 5
#include <stdio.h>int search(int arr[ROW], int len)
{if (arr == NULL || len <= 0){return;}int p1 = 0;int p2 = len - 1;int mid = p1;while (arr[p1] >= arr[p2]){if (p2 - p1 == 1){mid = p2;break;}mid = (p1 + p2) / 2;if (arr[mid] >= arr[p1]){p1 = mid;}else if (arr[mid] <= arr[p2]){p2 = mid;}}return arr[mid];}int main()
{int arr[ROW] = { 3, 4, 5, 1, 2 };printf("%d\n", search(arr, ROW));return 0;
}
- 运行结果为:
- 前面我们提到在旋转数组中,由于是把递增排序数组前面的若干个数字搬到数组的后面,因此第一个数字总是大于或者等于最后一个数字。
- 但按照定义还有一个特例:如果把排序数组的前面的0个元素搬到最后面,即排序数组本身,这仍然是数组的一个旋转,我们的代码需要支持这种情况。
- 此时,数组中的第一个数字就是最小的数字,可以直接返回。
- 这就是在上面的代码中,把 indexMid 初始化为 index1的原因。一旦发现数组中第一个数字小于最后一个数字,表明该数组是排序的,就可以直接返回第一个数字了。
3. 更完美的做法
- 上述代码是否就完美了呢?面试官会告诉我们其实不然。
- 他将提示我们再仔细分析下标为indexl和 index2(indexl和index2 分别和图中 P1和P2 相对应)的两个数相同的情况。
- 在前面的代码中,当这两个数相同,并且它们中间的数字(即 indexMid 指向的数字)也相同时,我们把 indexMid赋值给了 index1,也就是认为此时最小的数字位于中间数字的后面。
- 是不是一定这样?

- 注:在这两个数组中,第一个数字、最后一个数字和中间数字都是1,我们无法确定中间的数字 1 属于第一个递增子数组还是属于第二个递增子数组。第二个子数组用灰色背景表示。
- 在这两种情况中,第一个指针和第二个指针指向的数字都是1,并且两个指针中间的数字也是1,这3个数字相同。
- 在第一种情况中,中间数字(下标为 2)位于后面的子数组;在第二种情况中,中间数字(下标为2)位于
- 前面的子数组中。因此,当两个指针指向的数字及它们中间的数字三者相同的时候,我们无法判断中间的数字是位于前面的子数组中还是后面的子数组中,也就无法移动两个指针来缩小查找的范围。
- 此时,我们不得不采用顺序查找的方法。
- 把问题分析清楚了之后,我们就可以把代码修改为:
#define ROW 5
#include <stdio.h>int search_(int arr[ROW], int p1, int p2)
{int min = arr[p1];for (int i = p1 + 1; i <= p2; i++){if (arr[i] < min){min = arr[i];}}return min;
}int search(int arr[ROW], int len)
{if (arr == NULL || len <= 0){return;}int p1 = 0;int p2 = len - 1;int mid = p1;while (arr[p1] >= arr[p2]){if (p2 - p1 == 1){mid = p2;break;}mid = (p1 + p2) / 2;if (arr[p1] == arr[mid] && arr[mid] == arr[p2]){return search_(arr, p1, p2);}if (arr[mid] >= arr[p1]){p1 = mid;}else if (arr[mid] <= arr[p2]){p2 = mid;}}return arr[mid];
}int main()
{int arr[ROW] = { 1, 0, 1, 1, 1 };printf("%d\n", search(arr, ROW));return 0;
}
最后,
恭喜你又遥遥领先了别人!

相关文章:

剑指offer——旋转数组的最小数字
目录 1. 题目描述2. 分析思路2.1 示例分析 3. 更完美的做法 1. 题目描述 把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3.4,5,1.2}为{1.2,3,4,5}的一个旋转&a…...
盘点数据可视化大屏焦点图十种样式
所谓焦点图就是大屏中居于中心位置的图,是视觉的中心,本位列举了十种焦点图样式供大家参考。 地球作为焦点图 图片来自网络 地图作为焦点图 图片来自网络 城市作为焦点图 图片来自网络 园区做焦点图 图片来自网络 建筑做焦点图 图片来自网络 生产线…...

问题 G: 老鼠和猫的交易
题目描述 小老鼠准备了M磅的猫粮,准备去和看守仓库的猫做交易,因为仓库里有小老鼠喜欢吃的五香豆。 仓库有N个房间; 第i个房间有J[i] 磅的五香豆,并且需要用F[i]磅的猫粮去交换; 老鼠不必交换该房间所有的五香豆&…...
HiveSQL——借助聚合函数与case when行转列
一、条件函数 if 条件函数 if函数是最常用到的条件函数,其写法是if(xn,a,b), xn代表判断条件,如果xn时,那么结果返回a ,否则返回b。 selectif(age < 25 or age is null, 25岁以下, 25岁以上) as age_cnt,count(1) as number from table…...

冒泡排序,判断回文,以及12-24小时制
6-7 定义函数,完成冒泡排序算法。 本题定义一个冒泡排序算法的函数,调用函数后实现数组的升序排序,其数组长度为任意长度。 函数接口定义: 在这里描述函数接口。例如: void sort(int arr[],int n); 在这里解释接口…...

【Vue】computed与watch
📝个人主页:五敷有你 🔥系列专栏:Vue⛺️稳重求进,晒太阳 计算属性 概念:基于现有的数据,计算出来新的属性,依赖的数据变化,自动重新计算 语法: 声明…...
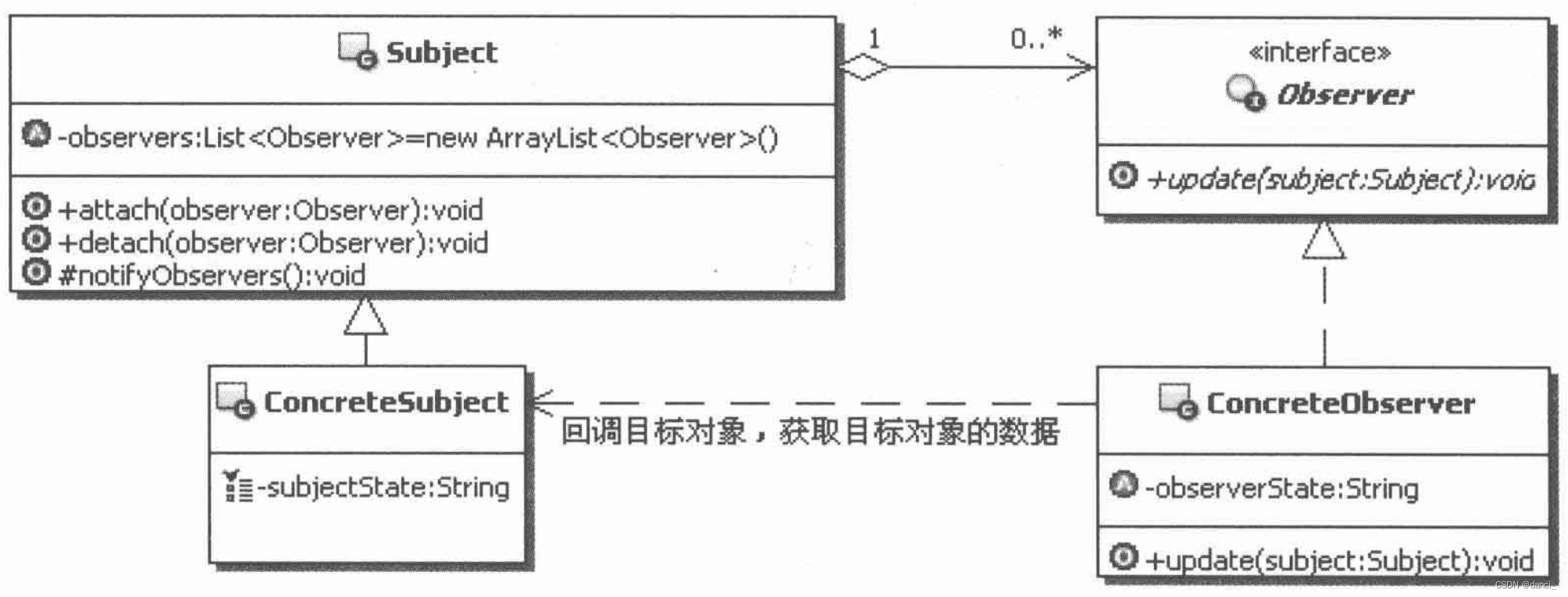
探索设计模式的魅力:捕捉变化的风-用观察者模式提升用户体验
设计模式专栏:http://t.csdnimg.cn/U54zu 目录 一、引言 核心概念 应用场景 可以解决的问题 二、场景案例 2.1 不用设计模式实现 2.2 存在问题 2.3 使用设计模式实现 2.4 成功克服 三、工作原理 3.1 结构图和说明 3.2 工作原理详解 3.3 实现步骤 四、 优…...
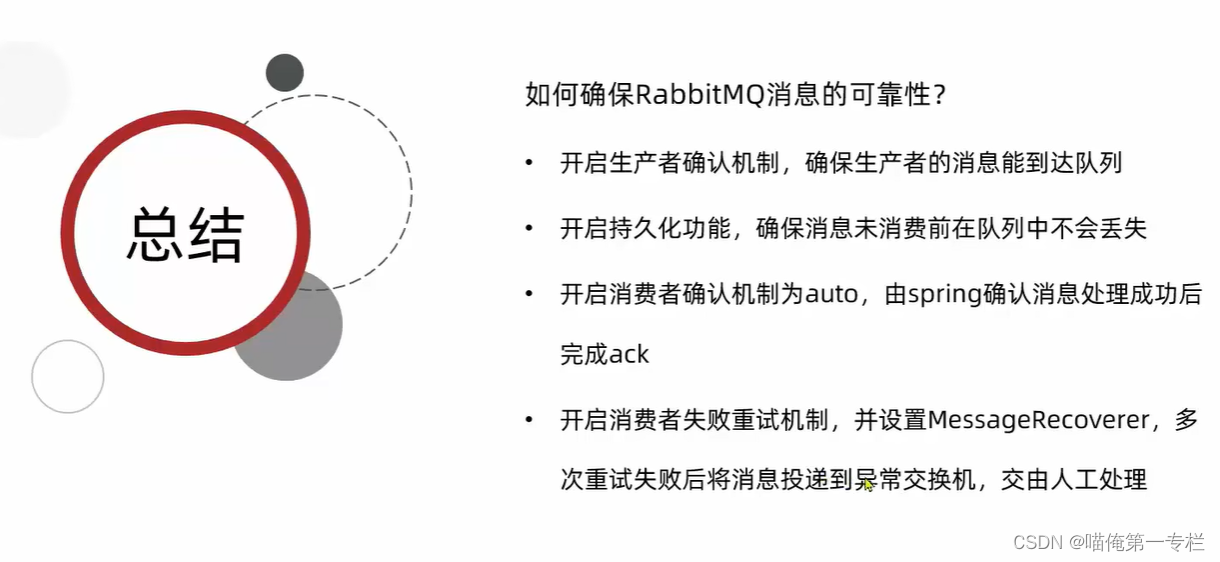
SpringCloud-高级篇(十九)
我们已经学过使用 SpringAMQP去收和发消息,但是发和收消息是只是MQ最基本的功能了,在收发消息的过程中,会有很多的问题需要去解决,下面需要学习rabbitMQ的高级特性去解决 死信交换机:这个可以帮助我们实现消息的延迟的…...

Junit常用断言
0.断言简介 断言:assert Q:断言的作用 更方便的对结果进行判定 "有针对性"的if判断 针对两个变量值是否相同 使用assertEquals针对两个对象是否相同 使用assertSame针对返回值是否为True 使用assertTrue 1.断言的参数 assertXXX(”断言失败时提升的信息“&#x…...
)
docker 实现 mysql:8.3.0 主从复制(2024年2月13日最新版本)
环境为 CentOS 7.6, 具体操作请看MySQL主从复制01-主从复制概述及原理_哔哩哔哩_bilibili 1、配置主服务器 # 启动主服务器 docker run -p 3306:3306 --name mysql_master -e MYSQL_ROOT_PASSWORDnmnmnm67890890 -v /docker/mysql_master/conf:/etc/mysql/conf.d…...
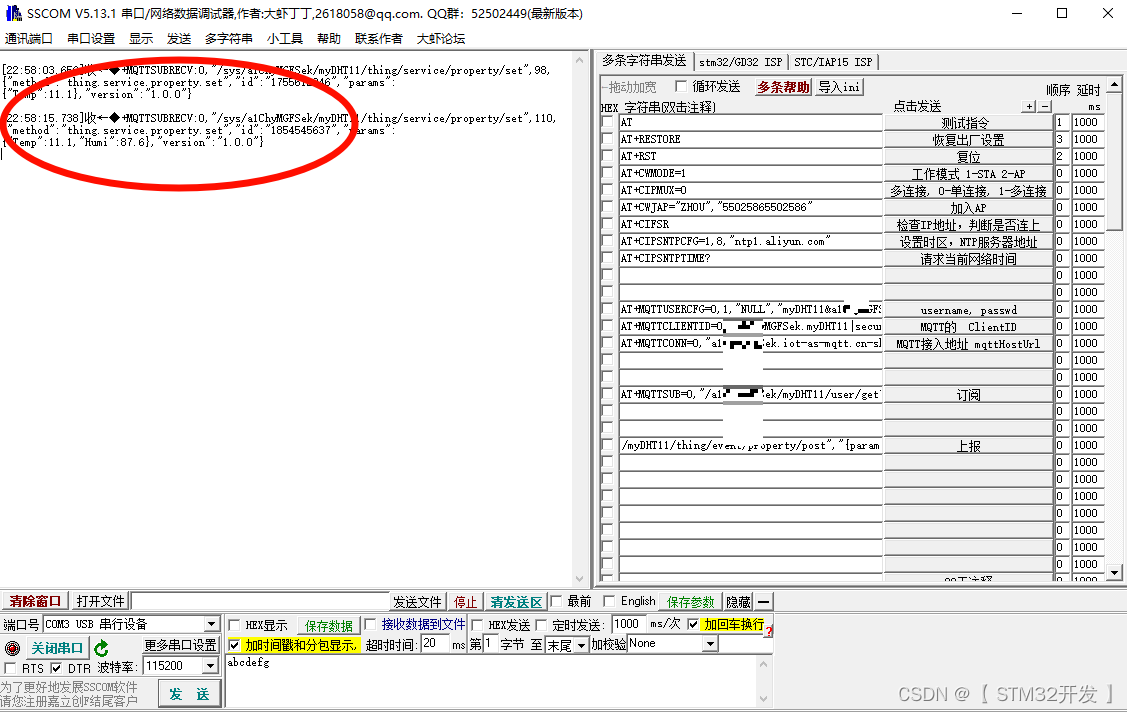
STM32 + ESP8266,连接阿里云 上报/订阅数据
(文章正在编辑中,一点点地截图操作过程,估计要拖拉两三天) 一、烧录MQTT固件 ESP8266出厂时,默认是AT固件。连接阿里云,需要使用MQTT固件。 1、独立EPS8266模块的烧录方法 2、魔女开发板,板载…...

如何利用chatgpt提升工作效率?
在数字化和信息化的时代,人工智能技术已经深入到了我们生活的方方面面。其中,ChatGPT作为当前热门的人工智能技术,以其强大的自然语言处理能力和广泛的应用场景,正逐渐改变着我们的工作方式,为我们提高工作效率提供了全…...

MongoDB聚合:$geoNear
$geoNear根据指定的点按照距离以由近到远的顺序输出文档。 从4.2版本开始,MongoDB移除了limit和num选项以及100个文档的限制,如果要限制结果文档的数量可以使用$limit阶段。 语法 { $geoNear: { <geoNear options> } }$geoNear操作接受一个包含…...

Docker-CE 国内源国内镜像
Docker-CE 就是 Docker Community Edition 的意思 docker-ce由docker官方维护 , docker.io由Debian维护 Docker官文 – Install Docker Engine on CentOS Docker官文 – Install Docker Engine on Fedora Docker官文 – Install Docker Engine on Debian Docker官文 – In…...
【Tauri】(3):使用Tauri1.5版本,进行桌面应用开发,在windows上搭建环境,安装node,rust环境,可以打包成功,使用vite创建应用
1,视频地址: https://www.bilibili.com/video/BV1Ny421a7nA/ 【Tauri】(3):使用Tauri1.5版本,进行桌面应用开发,在windows上搭建环境,安装node,rust环境,可以…...

C++ 堆排序
C 堆排序 堆排序是一种基于二叉堆数据结构的排序算法,其原理如下: 构建最大堆:将待排序的数组看作一个完全二叉树,并通过调整节点的位置构建一个最大堆。最大堆满足每个父节点的值都大于或等于其子节点的值。构建最大堆的过程可以…...
U3D记录之FBX纹理丢失问题
今天费老大劲从blender建了个模型,然后导出进去unity 发现贴图丢失 上网查了一下 首先blender导出要改设置 这个path mode要copy 然后unity加载纹理也要改设置 这里这个模型的纹理load要改成external那个模式 然后就有了,另外这个导出还有好多选项可…...

监测Nginx访问日志502情况后并做相应动作
今天带大家写一个比较实用的脚本哈 原理: 假设服务器环境为lnmp,近期访问经常出现502现象,且502错误在重启php-fpm服务后消失,因此需要编写监控脚本,一旦出现502,则自动重启php-fpm服务 场景: 1…...

【数据分享】1929-2023年全球站点的逐年平均风速(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、能见度等指标,说到气象数据,最详细的气象数据是具体到气象监测站点的数据! 有关气象指标的监测站点数据,之前我们分享过1929-2023年全球气象站…...

Android性能调优 - 应用安全问题
Android应用安全 1.组件暴露: 像比如ContentProvider,BroadcastReceiver,Activity等组件有android:exported属性; 如果是私有组件 android:exported “false”; 如果是公有组件 android:exported “true” 且进行权限控制&…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
