局部加权回归
局部加权回归(Local Weighted Regression)是一种非参数回归方法,用于解决线性回归模型无法很好拟合非线性数据的问题。它通过给不同的样本赋予不同的权重,使得在拟合模型时更加关注靠近目标点附近的样本数据。
局部加权回归的基本思想是对于给定的目标点,通过定义一个权重函数,对样本点进行加权,并利用加权的样本点来拟合回归模型。在预测新的数据点时,同样使用权重函数,对附近的样本点进行加权平均得到预测值。
局部加权回归的权重函数通常选择高斯核函数或者三角核函数,这些函数都是以目标点为中心的对称函数。权重函数的选择决定了拟合模型时对不同样本点的关注程度。对于靠近目标点的样本点,赋予较高的权重;对于远离目标点的样本点,赋予较低的权重。
局部加权回归具有灵活性和非线性建模能力,但是它也有一些缺点。由于每个目标点的回归模型都是针对附近的样本点进行建模的,因此在预测新的数据时,需要重新计算权重并进行局部拟合,计算量较大。另外,由于每个样本点都有可能参与到不同的目标点的回归模型中,因此在整体上缺乏稳定性。
局部加权回归的原理如下:
1. 给定一个目标点(待预测的数据点)和样本数据集。
2. 定义一个权重函数,通常选择高斯核函数或者三角核函数。该权重函数以目标点为中心,根据距离进行加权。靠近目标点的样本点被赋予较大的权重,远离目标点的样本点被赋予较小的权重。
3. 对于每个目标点,根据样本数据集中的样本点与目标点的距离以及权重函数的值,计算样本点的权重。
4. 根据样本点的权重,使用加权最小二乘法进行回归模型的拟合。通常使用线性回归模型。
5. 得到回归模型后,预测新的数据点时,使用相同的权重函数计算目标点附近样本点的权重,根据权重对样本点进行加权平均,得到预测值。
局部加权回归的关键在于权重函数的选择和权重的计算。通常可以根据实际问题进行调整,使得模型更加适应数据的分布。需要注意的是,由于每个目标点的回归模型都是针对附近的样本点进行建模的,因此在预测新的数据时,需要重新计算权重并进行局部拟合,计算量较大。另外,由于每个样本点都有可能参与到不同的目标点的回归模型中,因此在整体上缺乏稳定性。
局部加权回归具有以下几个特点:
1. 非参数性:局部加权回归不需要对数据的分布做出任何假设,不需要对数据进行参数化建模。因此,它可以适用于各种类型的数据,适用于非线性关系的数据。
2. 非线性性:由于权重函数的存在,局部加权回归可以捕捉到数据中的非线性关系。通过调整权重函数的形状和参数,可以更好地适应数据的特点。
3. 高灵活性:由于每个目标点都有自己的回归模型,因此局部加权回归非常灵活。它可以根据数据的不同情况,对不同的目标点进行不同的回归拟合。
4. 局部性:局部加权回归仅使用附近的样本点来拟合目标点的回归模型。因此,它更关注目标点周围的局部特征,对离目标点较远的样本点的影响较小。这使得局部加权回归对异常值或离群点的影响相对较小。
5. 计算量大:由于每个目标点都需要重新计算权重并进行局部拟合,局部加权回归的计算量较大。尤其当样本数据集较大时,计算时间会显著增加。
6. 缺乏稳定性:每个样本点都有可能参与到不同的目标点的回归模型中,导致在整体上缺乏稳定性。这使得局部加权回归对样本点的选取和权重的确定比较敏感。
总之,局部加权回归是一种灵活且适应性强的方法,能够捕捉到非线性关系,对异常值不敏感,但在计算量和稳定性方面存在一定的问题。
局部加权回归在以下情况下常常被使用:
1. 非线性关系建模:当数据中存在着非线性关系时,局部加权回归可以更好地捕捉到这种关系。比如,当自变量和因变量之间存在着曲线形状的关系时,局部加权回归可以提供更准确的拟合。
2. 异常值处理:局部加权回归对于异常值或离群点的影响较小,因为它主要关注目标点周围的局部特征。因此,当数据中存在着异常值或离群点时,局部加权回归可以提供更稳健的回归结果。
3. 非参数回归:局部加权回归不需要对数据的分布做出任何假设,不需要参数化建模。因此,它适用于各种类型的数据,即使数据的分布不符合常见的统计模型,也可以通过局部加权回归进行拟合。
4. 非平稳数据分析:当数据具有局部非平稳性时,局部加权回归可以用于分析数据中的局部特征。例如,时间序列数据中可能存在着局部趋势、季节性或周期性,局部加权回归可以用来建模和预测这些局部特征。
5. 数据探索和可视化:局部加权回归可以用于对数据进行探索和可视化。通过在数据中绘制局部加权回归的拟合曲线,可以更直观地观察到数据的趋势和关系,帮助分析人员进行更深入的数据理解。
总而言之,局部加权回归是一种适用于多种场景的非参数回归方法,特别适用于非线性关系建模、异常值处理、非平稳数据分析以及数据探索和可视化等应用。
下面是一个简单的局部加权回归的Python代码示例,用于拟合一组带有噪声的非线性数据:
import numpy as np
import matplotlib.pyplot as pltdef local_weighted_regression(x, y, query_point, tau):m = len(x)weights = np.exp(-0.5 * ((x - query_point) / tau) ** 2)X = np.column_stack((np.ones(m), x))W = np.diag(weights)theta = np.linalg.inv(X.T @ W @ X) @ X.T @ W @ yreturn theta[0] + theta[1] * query_point# 生成带噪声的非线性数据
np.random.seed(0)
x = np.linspace(-5, 5, 100)
y = np.sin(x) + np.random.normal(0, 0.2, 100)# 设定tau参数
tau = 0.5# 针对每个x点进行局部加权回归拟合
pred_y = [local_weighted_regression(x, y, query_point, tau) for query_point in x]# 绘制原始数据和拟合曲线
plt.scatter(x, y, label='Original Data')
plt.plot(x, pred_y, color='red', label='Locally Weighted Regression')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
该代码使用了高斯核函数作为权重,通过调整tau参数可以控制拟合曲线的平滑程度。在这个例子中,我们使用sin函数生成了带有噪声的非线性数据,并使用局部加权回归来拟合数据,最终将原始数据和拟合曲线绘制在同一张图上进行对比。
相关文章:

局部加权回归
局部加权回归(Local Weighted Regression)是一种非参数回归方法,用于解决线性回归模型无法很好拟合非线性数据的问题。它通过给不同的样本赋予不同的权重,使得在拟合模型时更加关注靠近目标点附近的样本数据。 局部加权回归的基本…...

国内国外最好的数据恢复软件评测,哪种数据恢复软件最有效?
随着数字和商业格局在多个领域不断发展,变得更加依赖数据,威胁数据的努力也同样存在。 计算机病毒、勒索软件和恶意软件是导致数据丢失的主要威胁,可能会让您的组织陷入停机或严重影响您的工作效率。而解决这个问题的方法就是数据恢复。 什么…...
bugku 1
Flask_FileUpload 文件上传 先随便传个一句话木马 看看回显 果然不符合规定 而且发现改成图片什么的都不行 查看页面源代码,发现提示 那应该就要用python命令才行 试试ls 类型要改成图片 cat /flag 好像需要密码 bp爆破 根据提示,我们先抓包 爆破 …...
C++ bfs再探迷宫游戏(五十五)【第二篇】
今天我们用bfs解决迷宫游戏。 1.再探迷宫游戏 前面我们已经接触过了迷宫游戏,并且学会了如何使用 DFS 来解决迷宫最短路问题。用 DFS 求解迷宫最短路有一个很大的缺点,需要枚举所有可能的路径,读入的地图一旦很大,可能的搜索方案…...
【Spring原理进阶】SpringMVC调用链+JSP模板应用讲解
🎉🎉欢迎光临🎉🎉 🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀 🌟特别推荐给大家我的最新专栏《Spring 狂野之旅:底层原理高级进阶》 🚀…...
23种计模式之Python/Go实现
目录 设计模式what?why?设计模式:设计模式也衍生出了很多的新的种类,不局限于这23种创建类设计模式(5种)结构类设计模式(7种)行为类设计模式(11种) 六大设计原则开闭原则里氏替换原…...

Qt可视化大屏布局
科技大屏现在非常流行,这里分享一下某个项目的大屏布局(忘了源码是哪个博主的了) 展示 这个界面整体是垂直布局,分为两个部分,标题是一个部分,然后下面的整体是一个layout布局,为另外一部分。 l…...

re:从0开始的CSS之旅 14. 显示模式的切换
1. 两个属性 display 属性可以用于转换元素的显示模式 可选值: block 转换为块元素 inline 转换为行内元素 inline-block 转换为行内块元素 none 不显示元素,并且不占用元素的位置 visibility 属性用于设置元素是否显示 可选值: visible 显示…...

K8S系列文章之 [Alpine基础环境配置]
用户手册:Alpine User Handbook 官方WIKI:Alpine Linux WIKI 安装 安装的实际逻辑是通过 setup-alpine 脚本去调用其他功能的脚本进行配置,可以通过 vi 查看脚本。如果某个部分安装失败,可退出后单独再次执行。通过镜像文件&a…...
单页404源码
<!doctype html> <html> <head> <meta charset"utf-8"> <title>简约 404错误页</title><link rel"shortcut icon" href"./favicon.png"><style> import url("https://fonts.googleapis.co…...

MySQL-运维
一、日志 1.错误日志 错误日志是MySQL中最重要的日志之一,它记录了当mysql启动和停止时,以及服务器在运行过程中发生任何严重错误时的相关性息。当数据库出现任何故障导致无法正常使用时,建议首先查看此日志。 该日志是默认开启的…...
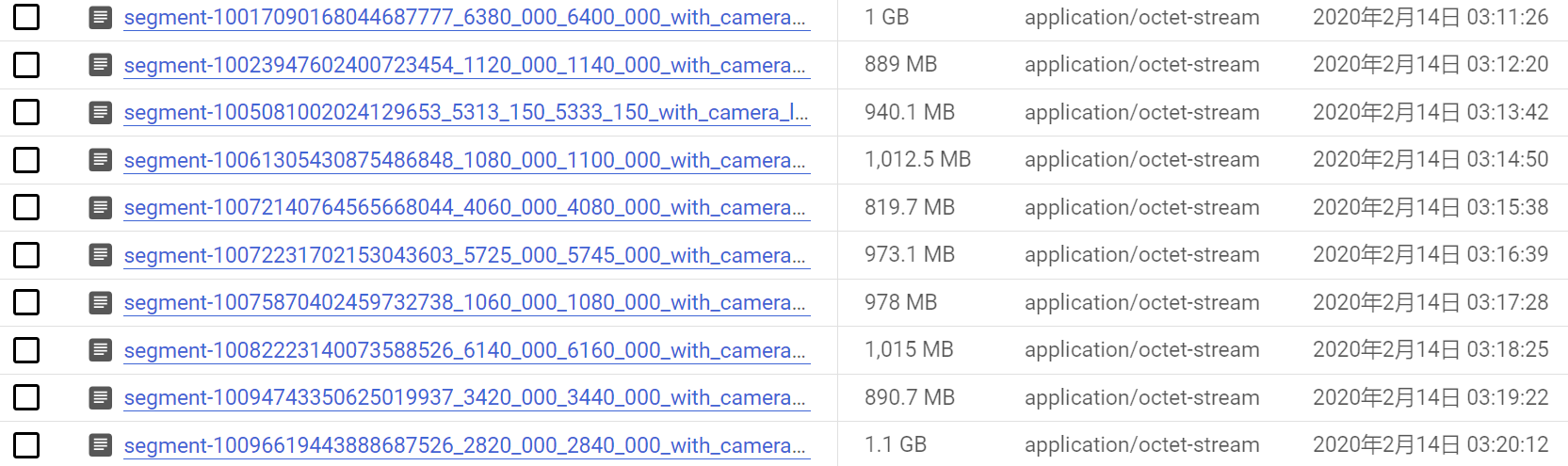
Waymo数据集下载与使用
在撰写论文时,接触到一个自动驾驶数据集Waymo Dataset 论文链接为:https://arxiv.org/abs/1912.04838v7 项目链接为:https://github.com/waymo-research/waymo-open-dataset 数据集链接为:https://waymo.com/open waymo提供了两种…...

蓝桥杯每日一题----素数筛
素数筛 素数筛的作用是筛选出[2,N]范围内的所有素数,本次主要讲解两种方法,分别是埃氏筛和欧拉筛。证明时会提到唯一分解定理,如果不知道的小伙伴可以先去学一学,那我们开始啦! 1.埃氏筛 主要思想:当找到…...
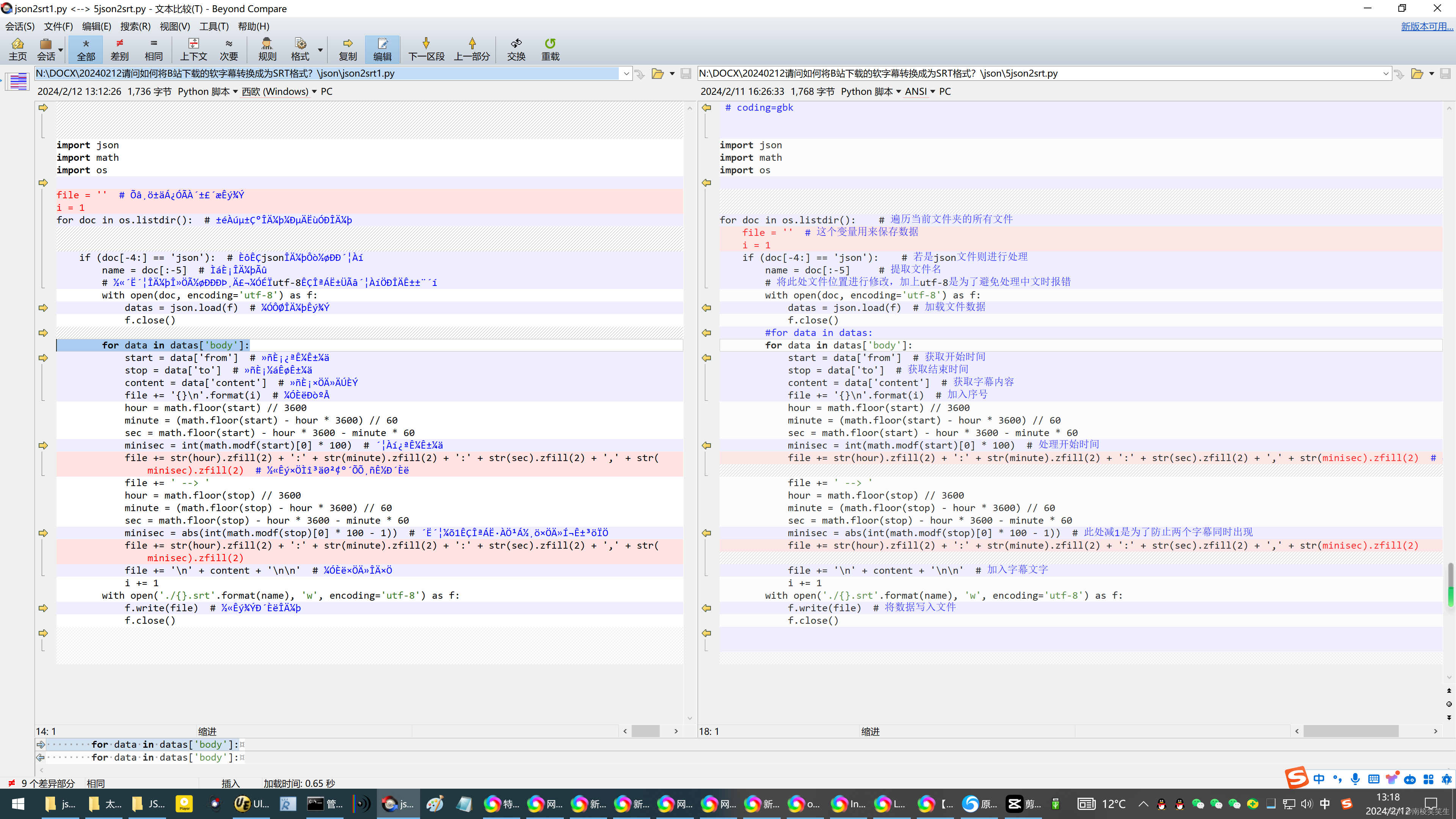
20240212请问如何将B站下载的软字幕转换成为SRT格式?
20240212请问如何将B站下载的软字幕转换成为SRT格式? 2024/2/12 12:47 百度搜索:字幕 json 转 srt json srt https://blog.csdn.net/a_wh_white/article/details/120687363?share_token2640663e-f468-4737-9b55-73c808f5dcf0 https://blog.csdn.net/a_w…...

《CSS 简易速速上手小册》第6章:高级 CSS 技巧(2024 最新版)
文章目录 6.1 使用 CSS 变量进行设计:魔法配方的调配6.1.1 基础知识6.1.2 重点案例:创建可定制的主题6.1.3 拓展案例 1:响应式字体大小6.1.4 拓展案例 2:使用 CSS 变量创建动态阴影效果 6.2 calc(), min(), max() 等函数的应用&am…...

2024-02-11 多进程、多线程 work
1. 创建一个多进程服务器和多线程服务器 a. 多进程 #include<myhead.h> #define PORT 9999 //端口号 #define IP "192.168.125.113" //IP地址//定义信号处理函数,用于回收僵尸进程 void handler(int signo) {if(signo S…...

详解结构体内存对齐及结构体如何实现位段~
目录 编辑 一:结构体内存对齐 1.1对齐规则 1.2.为什么存在内存对齐 1.3修改默认对齐数 二.结构体实现位段 2.1什么是位段 2.2位段的内存分配 2.3位段的跨平台问题 2.4位段的应用 2.5位段使用的注意事项 三.完结散花 悟已往之不谏,知来者犹可…...
Linux网络编程——tcp套接字
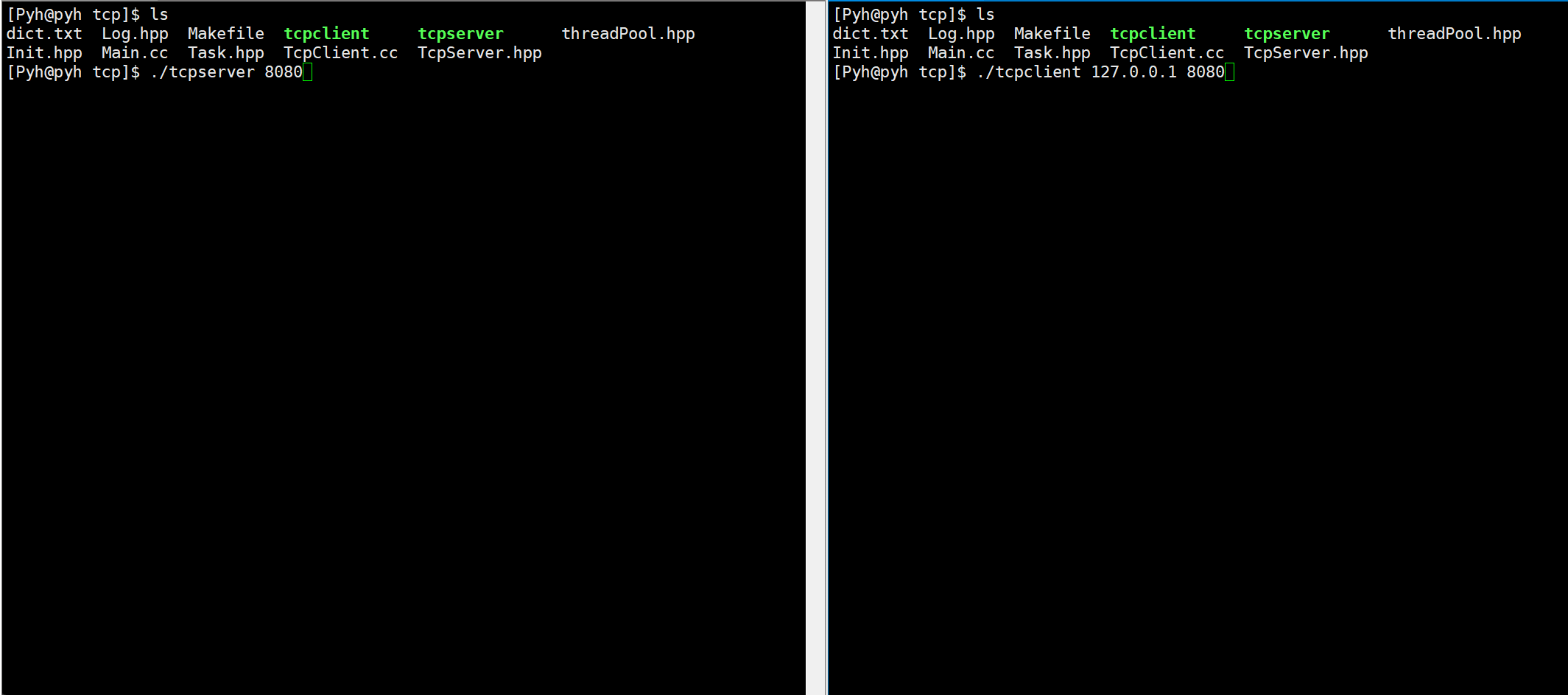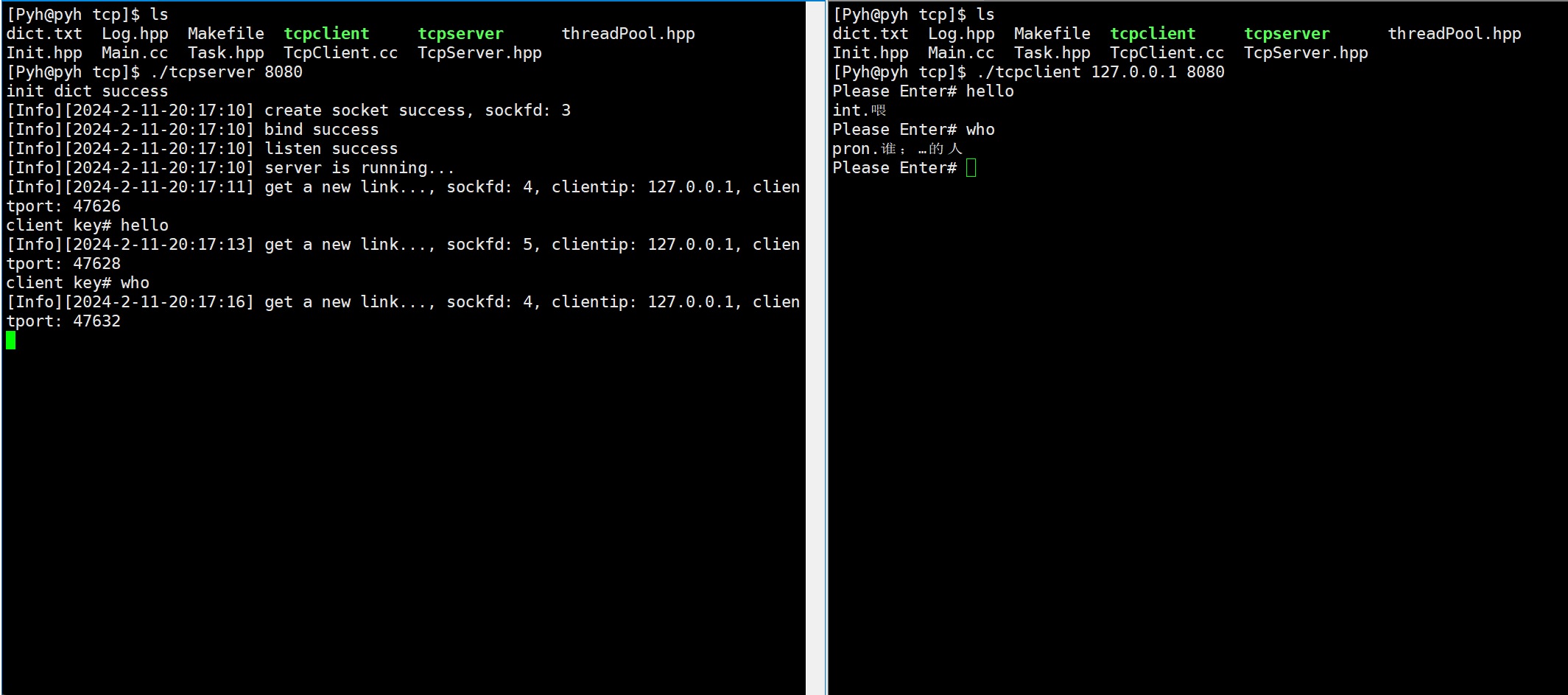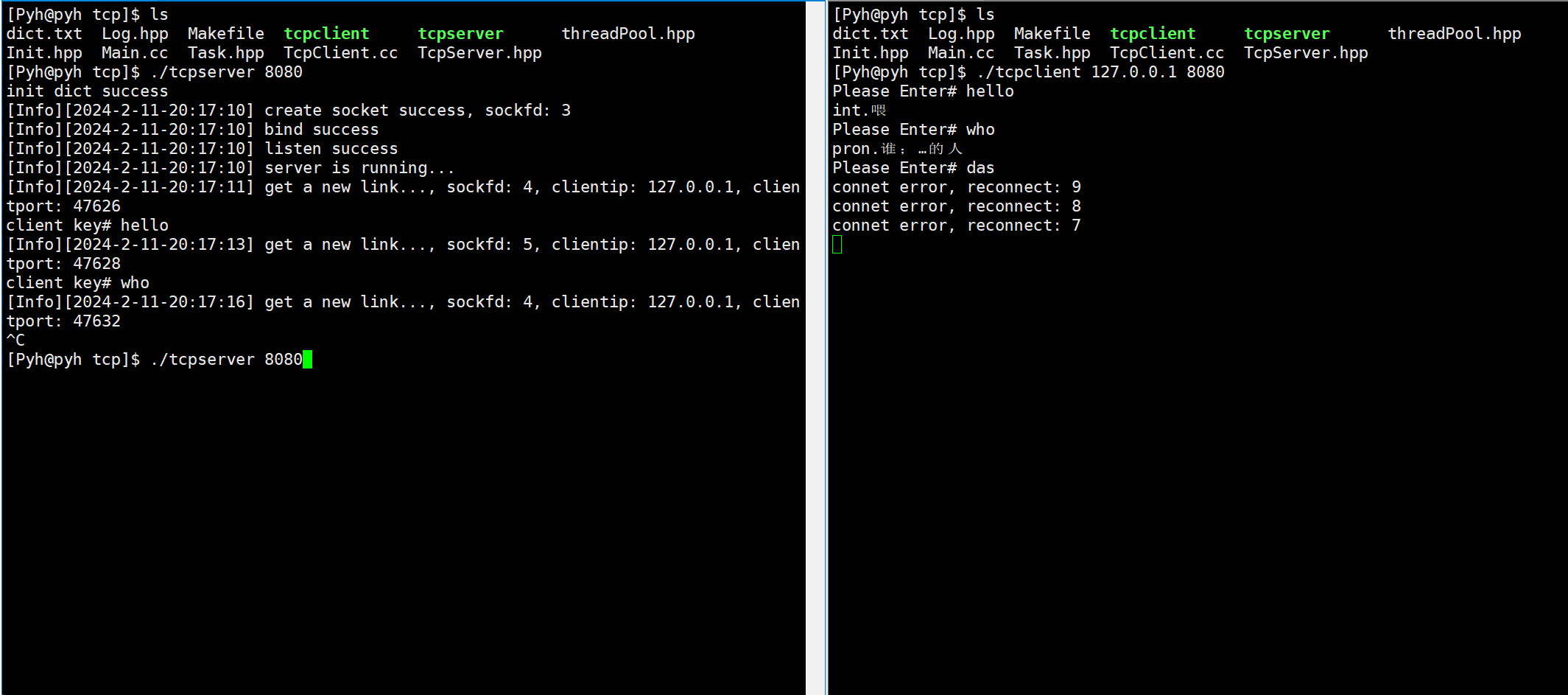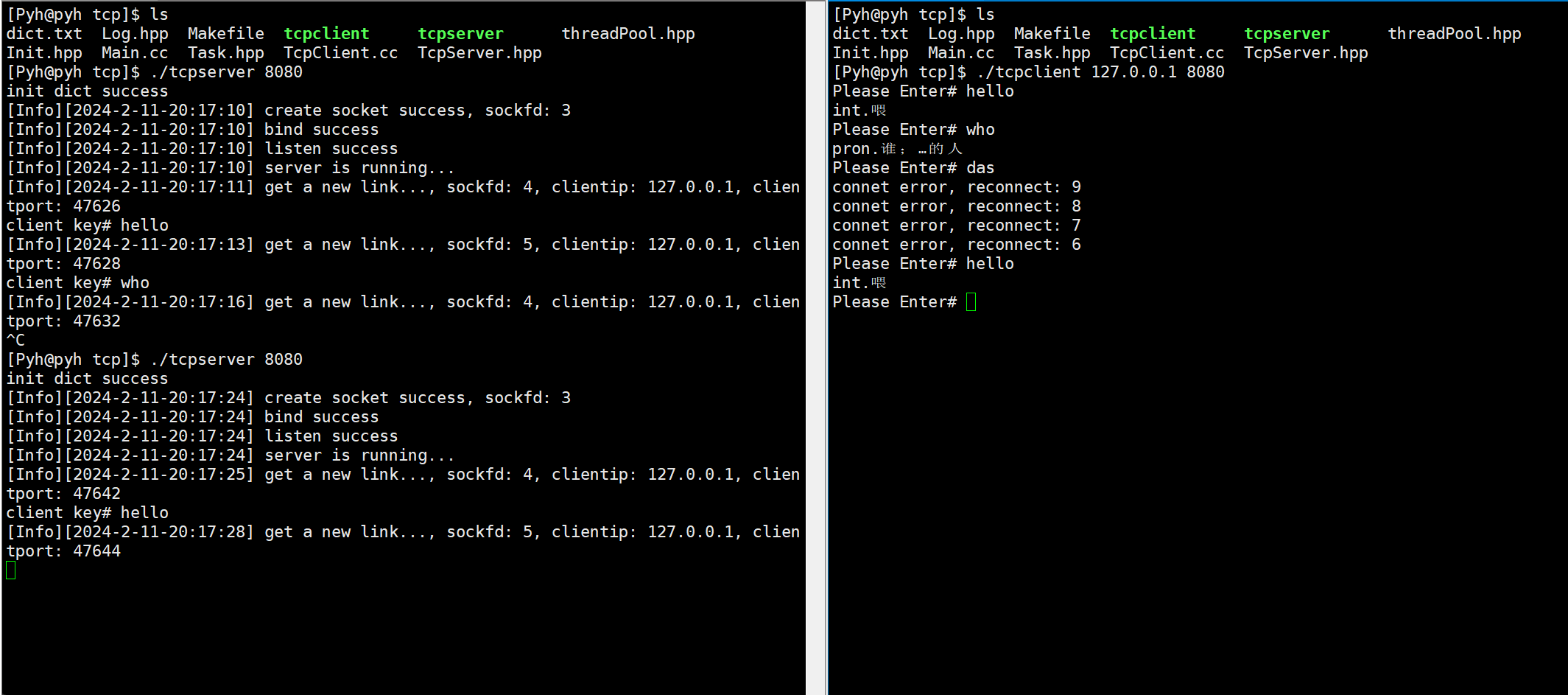
文章目录 主要代码关于构造listen监听accepttelnet测试读取信息掉线重连翻译服务器演示 本章Gitee仓库:tcp套接字 主要代码 客户端: #pragma once#include"Log.hpp"#include<iostream> #include<cstring>#include<sys/wait.h…...

【计算机网络】协议层次及其服务模型
协议栈(protocol stack) 物理层链路层网络层运输层应用层我们自顶向下,所以从应用层开始探究应用层 协议 HTTP 提供了WEB文档的请求和传送SMTP 提供电子邮件报文的传输FTP 提供两个端系统之间的文件传输报文(message)是…...

prometheus之redis_exporter部署
下载解压压缩包 mkdir /opt/redis_exporter/ cd /opt/redis_exporter/ wget http://soft.download/soft/linux/prometheus/redis_exporter/redis_exporter-v1.50.0.linux-amd64.tar.gz tar -zxvf redis_exporter-v1.50.0.linux-amd64.tar.gz ln -s /opt/redis_exporter/redis_…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
